Day 44 | 动态规划 完全背包、518. 零钱兑换 II 、 377. 组合总和 Ⅳ
完全背包
题目
文章讲解
视频讲解
完全背包和0-1背包的区别在于:物品是否可以重复使用
思路:对于完全背包问题,内层循环的遍历方式应该是从weight[i]开始一直遍历到V,而不是从V到weight[i]。这样可以确保每种物品可以被选择多次放入背包,从而求解完全背包问题。
对于完全背包问题,需要对内层循环进行调整,以确保每种物品可以被选择多次放入背包。
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt(); // 研究材料种类int V = sc.nextInt(); // 行李箱空间int[] values = new int[N]; // 物品价值int[] weight = new int[N]; // 物品重量// 依次输入每种物品的重量和价值for (int i = 0; i < N; i++) {weight[i] = sc.nextInt(); // 物品重量values[i] = sc.nextInt(); // 物品价值}int[] dp = new int[V + 1]; // 动态规划数组for (int i = 0; i < N; i++) {for (int j = weight[i]; j <= V; j++) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + values[i]); // 动态规划状态转移方程}}System.out.println(dp[V]); // 输出结果}
}一维0-1背包求解法示例如下
import java.util.*;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt(); // 研究材料种类int V = sc.nextInt(); // 行李箱空间int[] values = new int[N]; // 物品价值int[] weight = new int[N]; // 物品重量// 依次输入每种物品的重量和价值for (int i = 0; i < N; i++) {weight[i] = sc.nextInt(); // 物品重量values[i] = sc.nextInt(); // 物品价值}int[] dp = new int[V + 1]; // 动态规划数组for (int i = 0; i < N; i++) {for (int j = V; j >= weight[i]; j--) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + values[i]); // 动态规划状态转移方程}}System.out.println(dp[V]); // 输出结果}
}对比:
-
完全背包:
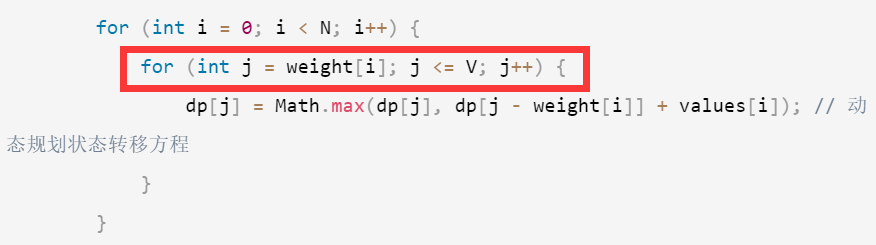
-
0-1背包:
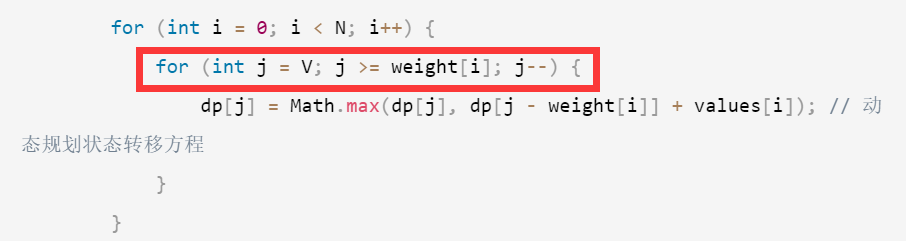
518. 零钱兑换 II
题目
文章讲解
视频讲解
思路:
- dp[j]:凑成总金额j的货币组合数为dp[j]
- 递推公式:dp[j] 就是所有的dp[j - coins[i]](考虑coins[i]的情况)相加
- 初始化需要注意 dp[0]=1;
class Solution {public int change(int amount, int[] coins) {int[] dp = new int[amount + 1];dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {dp[j] += dp[j - coins[i]];}}return dp[amount];}
}
377. 组合总和 Ⅳ
题目
文章讲解
视频讲解
思路:
如果求组合数就是外层for循环遍历物品,内层for遍历背包;
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j])dp[i] += dp[i - nums[j]];}}return dp[target];}
}
相关文章:

Day 44 | 动态规划 完全背包、518. 零钱兑换 II 、 377. 组合总和 Ⅳ
完全背包 题目 文章讲解 视频讲解 完全背包和0-1背包的区别在于:物品是否可以重复使用 思路:对于完全背包问题,内层循环的遍历方式应该是从weight[i]开始一直遍历到V,而不是从V到weight[i]。这样可以确保每种物品可以被选择多次…...
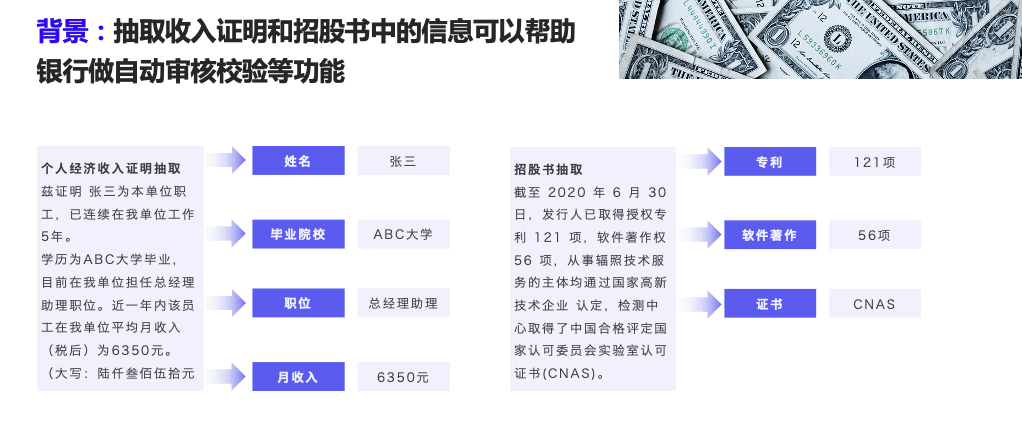
使用PaddleNLP UIE模型提取上市公司PDF公告关键信息
项目地址:使用PaddleNLP UIE模型抽取PDF版上市公司公告 - 飞桨AI Studio星河社区 (baidu.com) 背景介绍 本项目将演示如何通过PDFPlumber库和PaddleNLP UIE模型,抽取公告中的相关信息。本次任务的PDF内容是破产清算的相关公告,目标是获取受理…...
软件工程师,OpenAI Sora驾到,快来围观
概述 近期,OpenAI在其官方网站上公布了Sora文生视频模型的详细信息,展示了其令人印象深刻的能力,包括根据文本输入快速生成长达一分钟的高清视频。Sora的强大之处在于其能够根据文本描述,生成长达60秒的视频,其中包含&…...

【Linux 04】编辑器 vim 详细介绍
文章目录 🌈 Ⅰ 基本概念🌈 Ⅱ 基本操作1. 进入 / 退出 vim2. vim 模式切换 🌈 Ⅲ 命令模式1. 光标的移动2. 复制与粘贴3. 剪切与删除4. 撤销与恢复 🌈 Ⅳ 底行模式1. 保存文件2. 查找字符3. 退出文件4. 替换内容5. 显示行号6. 外…...

KMP算法详解
1. 问题引入 链接:leetcode_28 题目:s1字符串是否包含s2字符串,如果包含返回s1中包含s2的最左开头位置,不包含返回-1 暴力方法就是s1的每个位置都做开头,然后去匹配s2整体,时间复杂度O(n*m) KMP算法可以…...
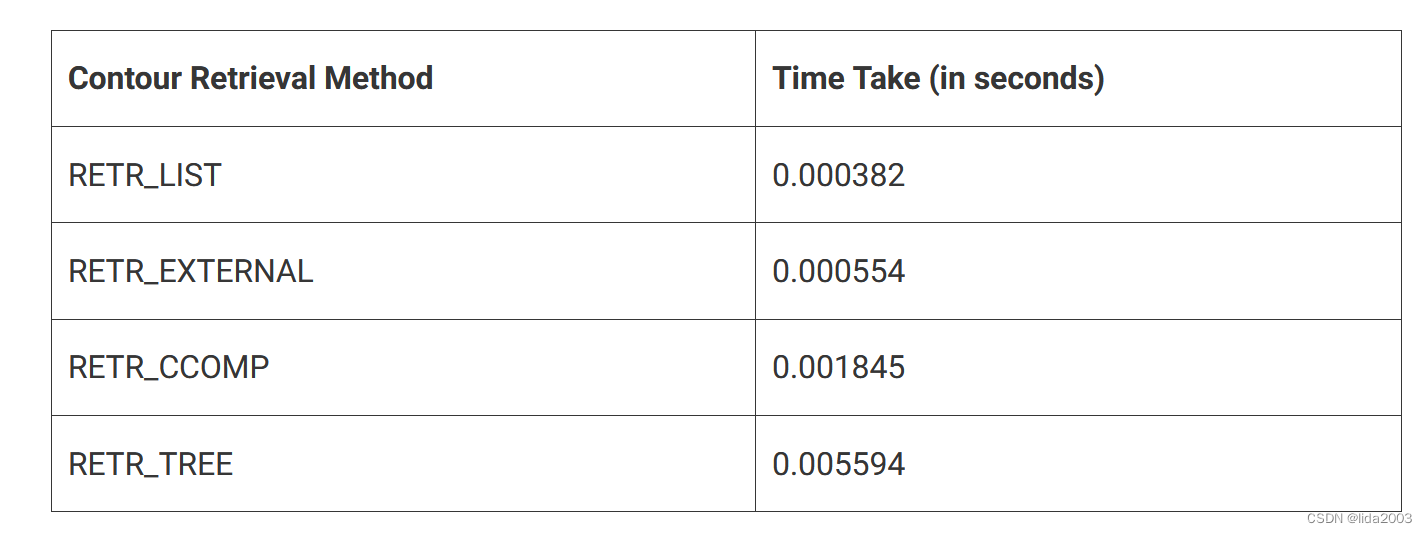
ubuntu22.04@laptop OpenCV Get Started: 013_contour_detection
ubuntu22.04laptop OpenCV Get Started: 013_contour_detection 1. 源由2. 应用Demo2.1 C应用Demo2.2 Python应用Demo 3. contour_approx应用3.1 读取图像并将其转换为灰度格式3.2 应用二进制阈值过滤算法3.3 查找对象轮廓3.4 绘制对象轮廓3.5 效果3.6 CHAIN_APPROX_SIMPLE v.s…...
[ai笔记5] 个人AI资讯助手实战
欢迎来到文思源想的ai空间,这是技术老兵重学ai以及成长思考的第5篇分享,也是把ai场景化应用的第一篇实操内容! 既然要充分学习和了解ai,自然少不了要时常看看ai相关资讯,所以今天特地用字节的“扣子”做了一个ai的资讯…...
)
QT+OSG/osgEarth编译之八十九:osgdb_ply+Qt编译(一套代码、一套框架,跨平台编译,版本:OSG-3.6.5插件库osgdb_ply)
文章目录 一、osgdb_ply介绍二、文件分析三、pro文件四、编译实践一、osgdb_ply介绍 斯坦福三角形格式(Stanford Triangle Format)是一种用于存储三维模型数据的文件格式,也称为 PLY 格式。它最初由斯坦福大学图形实验室开发,用于存储和共享三维扫描和计算机图形数据。 P…...

机器人专题:我国机器人产业园区发展现状、问题、经验及建议
今天分享的是机器人系列深度研究报告:《机器人专题:我国机器人产业园区发展现状、问题、经验及建议》。 (报告出品方:赛迪研究院) 报告共计:26页 机器人作为推动工业化发展和数字中国建设的重要工具&…...

算法沉淀——哈希算法(leetcode真题剖析)
算法沉淀——哈希算法 01.两数之和02.判定是否互为字符重排03.存在重复元素04.存在重复元素 II05.字母异位词分组 哈希算法(Hash Algorithm)是一种将任意长度的输入(也称为消息)映射为固定长度的输出的算法。这个输出通常称为哈希…...
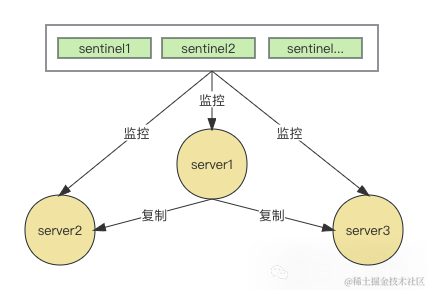
深入理解Redis哨兵原理
哨兵模式介绍 在深入理解Redis主从架构中Redis 的主从架构中,由于主从模式是读写分离的,如果主节点(master)挂了,那么将没有主节点来服务客户端的写操作请求,也没有主节点给从节点(slave&#…...
)
MySQL-存储过程(PROCEDURE)
文章目录 1. 什么是存储过程?2. 存储过程的优点3. MySQL中的变量3.1 系统变量3.2 用户自定义变量3.3 局部变量 4. 存储过程的相关语法4.1 创建存储过程(CREATE)4.2 查看存储过程(SHOW)4.3 修改存储过程(ALT…...
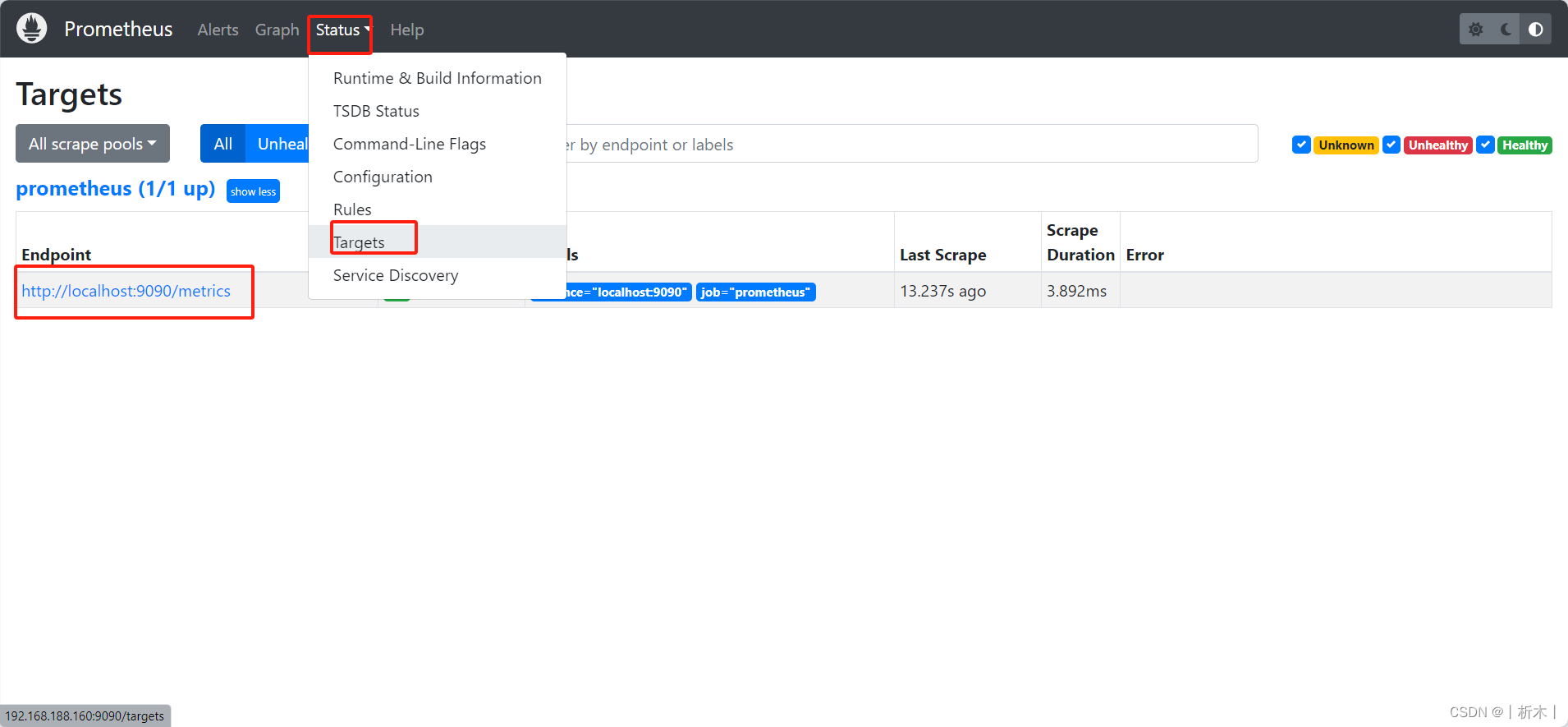
linux系统监控工具prometheus的安装以及监控mysql
prometheus 安装服务端客户端监控mysql prometheus浏览器查看 安装 https://prometheus.io/download/下载客户端和服务端以及需要监控的所有的包服务端 官网下载下载prometheustar -xf prometheus-2.47.2.linux-amd64.tar.gz -C /usr/local/ cd /usr/local/ mv prometheus-2.…...

初识tensorflow程序设计模式
文章目录 建立计算图tensorflow placeholdertensorflow数值运算常用的方法 tensorboard启动tensorboard的方法 建立一维与二维张量建立一维张量建立二维张量建立新的二维张量 矩阵的基本运算矩阵的加法矩阵乘法与加法 github地址https://github.com/fz861062923/TensorFlow 建…...
)
【QT+QGIS跨平台编译】之三十八:【GDAL+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、gdal介绍二、文件下载三、文件分析四、pro文件五、编译实践一、gdal介绍 GDAL(Geospatial Data Abstraction Library)是一个用于读取、写入和处理地理空间数据的开源库。它支持多种栅格和矢量地理空间数据格式,包括常见的GeoTIFF、Shapefile、NetCDF、HDF5等,…...

黑马鸿蒙教程学习1:Helloworld
今年打算粗略学习下鸿蒙开发,当作兴趣爱好,通过下华为那个鸿蒙开发认证, 发现黑马的课程不错,有视频和完整的代码和课件下载,装个devstudio就行了,建议32G内存。 今年的确是鸿蒙大爆发的一年呀,…...
)
蓝桥杯每日一题------背包问题(四)
前言 前面讲的都是背包的基础问题,这一节我们进行背包问题的实战,题目来源于一位朋友的询问,其实在这之前很少有题目是我自己独立做的,我一般习惯于先看题解,验证了题解提供的代码是正确的后,再去研究题解…...

OpenAI发布Sora技术报告深度解读!真的太强了!
😎 作者介绍:我是程序员洲洲,一个热爱写作的非著名程序员。CSDN全栈优质领域创作者、华为云博客社区云享专家、阿里云博客社区专家博主、前后端开发、人工智能研究生。公粽号:洲与AI。 🎈 本文专栏:本文收录…...
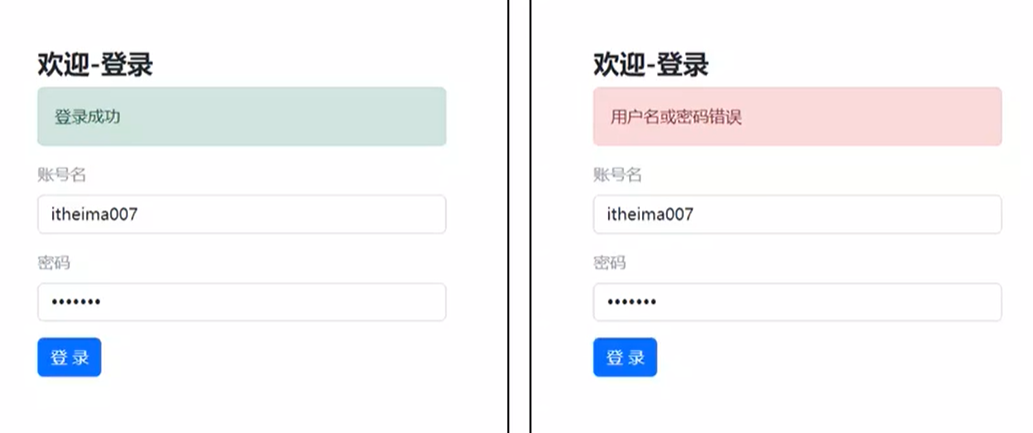
AJAX——接口文档
1 接口文档 接口文档:描述接口的文章 接口:使用AJAX和服务器通讯时,使用的URL,请求方法,以及参数 传送门:AJAX阶段接口文档 <!DOCTYPE html> <html lang"en"><head><meta c…...

leetcode hot100不同路径
本题可以采用动态规划来解决。还是按照五部曲来做 确定dp数组:dp[i][j]表示走到(i,j)有多少种路径 确定递推公式:我们这里,只有两个移动方向,比如说我移动到(i,j&#x…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
