随机过程及应用学习笔记(一)概率论(概要)
概率是随机的基础,在【概率论(概要)】这个部分中仅记录学习随机过程及应用的基本定义和结果。
 前言
前言
首先,概率论研究的基础是概率空间。概率空间由一个样本空间和一个概率测度组成,样本空间包含了所有可能的结果, 而概率测度则描述了每个结果发生的可能性大小。研究者通过定义适当的概率测度,可以更准确地描述各种随机现象的发生概率。
一、概率空间 (Ω,F,P)
Sample space 样本空间:随机试验的所有可能结果构成的集合称为样本空间,记为 Ω。(注:每个结果需要互斥,所有可能结果必须被穷举)
Set of events 事件集合,是Ω的一些子集构成的集合,记为 F,并且它需要满足以下三点特性(也就是必须是δ-field)
Probability measure 概率测度(或概率),描述一次随机试验中被包含在F 中的所有事件的可能性,记为P。
- 样本点(Sample point):随机试验E的每一个最简单的试验结果,记为
。
- 样本空间( Sample space):全体样本点构成的集合,称为样本空间Ω
- 事件(Event):
- 样本空间的子集组成的集类F,称为随机事件体(域)。
- 随机事件体F的任意元素A称为随机事件。
- 样本空间o和F的二元体(Ω,F)称为可测空间。
- 概率(Probability):每个事件一个可能性的度量值。
1、随机试验
定义:如果一个实验E,满足下列条件:
- 在相同的条件下可以重复进行;
- 每次试验的结果不止一个,并且能事先明确试验的所有结果;
- 一次试验结束之前,不能确定哪一个结果会出现。
称此试验为随机试验。 随机试验(Experiment):结果无法预先确定的试验。 随机试验的结果,称为事件。
2、集论初步
- 在概率论中,事件和事件的集合起主要作用。
- 事件的数学理论和集论有密切关系,用集论描述随机过程的事件。
把为了某种目的而研究的对象全体称为集合,简称为集。有某些特定性质的对象的全体,每一个属于这种集的对象,称为集元素。集合用大写字母A、B、C、…表示,元素用小写字母a、b、c、e、w、…表示,一些集组成的集叫类,我们用草写字母表示。
- 不包含任何元素的集合称为空集
- 包含所研究问题的全体对象,即:包含所考虑的所有集的所有元素的“最大”集合,称为空间Ω
集合的运算:

3、样本空间、随机事件体
随机试验E的每一个最简单的试验结果,称为样本点,记为。全体样本点构成的集合,称为样本空间,记为Ω。

集合论和概率论的专业术语对应关系如下表所示:

4、概率与概率空间

概率的性质与基本公式:

(6)连续性

5、条件概率

6、乘法公式事件的独立性
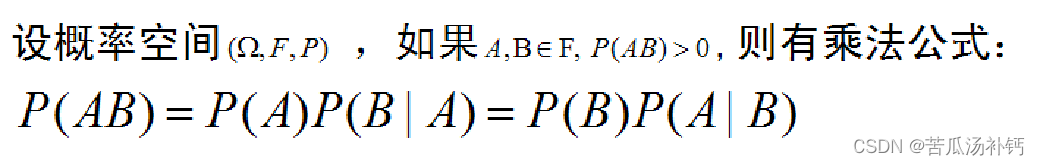
随机事件的独立性:

7、全概率公式与贝叶斯公式

二、随机变量及其分布
1、随机变量

2、分布函数

3、离散型随机变量及其分布律

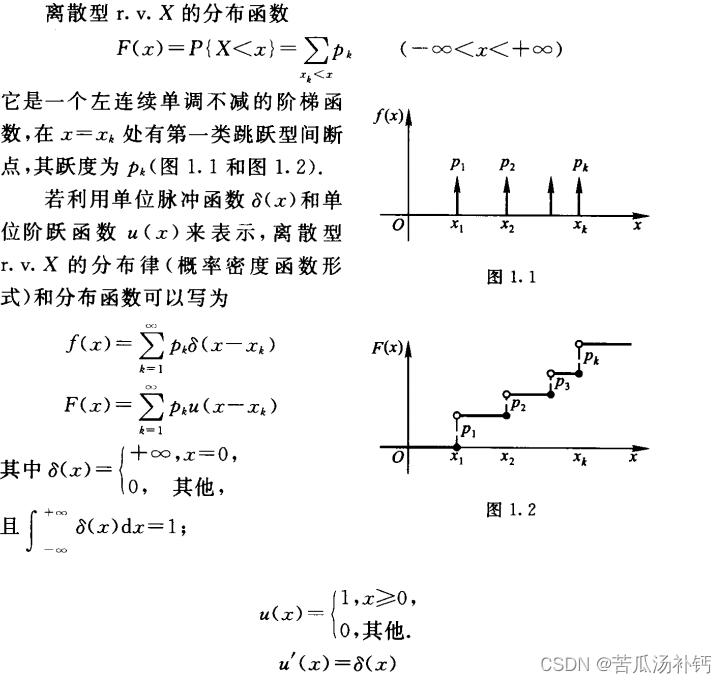
4、连续型随机变量

5、常见的随机变量及其分布
两点分布
两点分布(也称为伯努利分布)是概率论中一种离散概率分布,描述了一个随机变量取两个可能值之一的情况。这两个可能的取值通常被标记为0和1,或者成功和失败。该分布得名的原因是它只涉及到两个点。
两点分布的概率质量函数(PMF)可以表示为:

其中,p 是成功的概率,1−p 是失败的概率。这样的分布通常用于描述一次伯努利试验的结果,其中只有两个可能的结果。
两点分布的期望值(均值)和方差分别为:
- E(X)=p
- Var(X)=p(1−p)
其中,X 是随机变量,p 是成功的概率。
二项分布
二项分布(Binomial Distribution)是概率论中一种离散概率分布,描述了在进行一系列独立的伯努利试验中成功的次数。每次试验只有两种可能的结果,通常称为成功(success)和失败(failure)。
假设进行了 n 次独立的伯努利试验,每次试验成功的概率为 p,失败的概率为 1−p。随机变量 �X 表示成功的次数,则 X 的概率质量函数(Probability Mass Function,PMF)为:
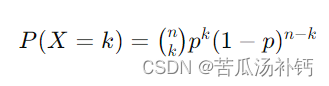
其中,(kn) 表示组合数,即从 n 次试验中选择 k 次成功的组合数。
二项分布的期望值(均值)和方差分别为:
E(X)=np
Var(X)=np(1−p)
这表明在进行多次独立的伯努利试验时,成功的次数的期望值等于每次试验成功的概率乘以试验次数,方差等于期望值乘以失败的概率。
二项分布在概率论和统计学中广泛应用,特别是在描述二元事件的发生次数的情况下,如硬币抛掷、医学研究中的治疗效果、制造业的质检等。
均匀分布
在二维均匀分布中,随机变量(X,Y) 在一个矩形区域内均匀分布。概率密度函数为:

其中,区域的面积决定了概率密度的大小。
均匀分布具有简单且直观的性质,适用于许多实际问题的建模,例如在一定范围内的随机实验或随机变量。均匀分布在统计学、概率论、模拟和随机过程等领域中经常被使用。
高斯分布
高斯分布,也被称为正态分布(Normal Distribution),是概率论和统计学中最为重要的分布之一。它具有许多重要的性质,对于自然界中的许多现象和实验结果都有很好的描述。
高斯分布的概率密度函数(Probability Density Function,PDF)为:

其中,x 是随机变量的取值,μ 是均值(期望值),σ 是标准差。这个分布的图像呈钟形,关于均值对称。
高斯分布的期望值(均值)为 μ,方差为 2σ2。标准差 σ 控制了曲线的宽度,曲线越宽表示数据越分散。
高斯分布在自然界中的许多现象中都能够找到,比如测量误差、身高分布、温度分布等。中心极限定理表明,当独立随机变量的和足够多时,它们的分布趋向于高斯分布。这使得高斯分布在统计学和概率论中被广泛应用,特别是在推断统计、假设检验和机器学习等领域。
三、随机变量的数字特征
1、数字期望

2、方差

3、矩、协方差


4、随机变量数字特征的性质
四、条件数学期望
五、特征函数
1、定义与性质
一般而言,对于随机变量X的分布,大家习惯用概率密度函数来描述,虽然概率密度函数理解起来很直观,但是确实随机变量的分布还有另外的描述方式,比如特征函数。
- 特征函数的本质是概率密度函数的泰勒展开
- 每一个级数表示原始概率密度函数的一个特征
- 如果两个分布的所有特征都相同,那我们就认为这是两个相同的分布
- 矩是描述概率分布的重要特征,期望、方差等概念都是矩的特殊形态
随机变量X的特征函数:
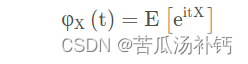
其中,i是虚数单位,t是任意实数,E[⋅]表示期望。
性质:
-
存在性: 对于任何随机变量X,它的特征函数总是存在的。
-
唯一性: 不同的随机变量可能具有相同的特征函数,但如果两个随机变量的特征函数在某个范围内相等,则它们在分布上相同。
-
特征函数与分布的关系: 如果两个随机变量具有相同的特征函数,则它们具有相同的分布。
-
特征函数的对称性: 如果X是一个实随机变量,其特征函数为φ(t),则对于任意实数t,有 ϕ(−t)=ϕ(t),其中ϕ(t)表示φ(t)的共轭复数。
-
特征函数的加法性: 如果X和Y是相互独立的随机变量,它们的特征函数分别为φX(t)和φY(t),那么它们的和Z = X + Y 的特征函数为 ϕZ(t)=ϕX(t)⋅ϕY(t)。
-
中心极限定理: 如果X1, X2, ..., Xn是独立同分布的随机变量,具有相同的期望μ和方差σ^2,则它们的和标准化后的特征函数在n趋于无穷大时趋近于正态分布的特征函数。
特征函数在概率论和统计学中有广泛的应用,它提供了一种便捷的方式来研究随机变量的性质和相互关系。
针对概率密度函数为f ( x )的连续随机变量X,特征函数写作:
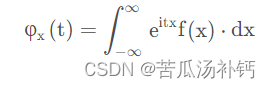
2、多维随机变量的特征函数

-
存在性: 对于任何多维随机变量 X,其特征函数总是存在的。
-
唯一性: 不同的随机变量可能具有相同的特征函数,但如果两个随机变量的特征函数在某个范围内相等,则它们在分布上相同。
-
特征函数与分布的关系: 如果两个多维随机变量具有相同的特征函数,则它们具有相同的分布。
-
特征函数的对称性: 如果多维随机变量 X 的特征函数为ϕX(t),则对于任意实数向量 t,有 ϕX(−t)=ϕX(t),其中 ϕX(t) 表示特征函数的共轭复数。
-
多维随机变量的独立性: 如果多维随机变量 X 和 Y 是相互独立的,它们的特征函数分别为 ϕX(t) 和 ϕY(t),那么它们的组合 Z=X+Y 的特征函数为 ϕZ(t)=ϕX(t)⋅ϕY(t)。
六、收敛性与极限定理
1、收敛性

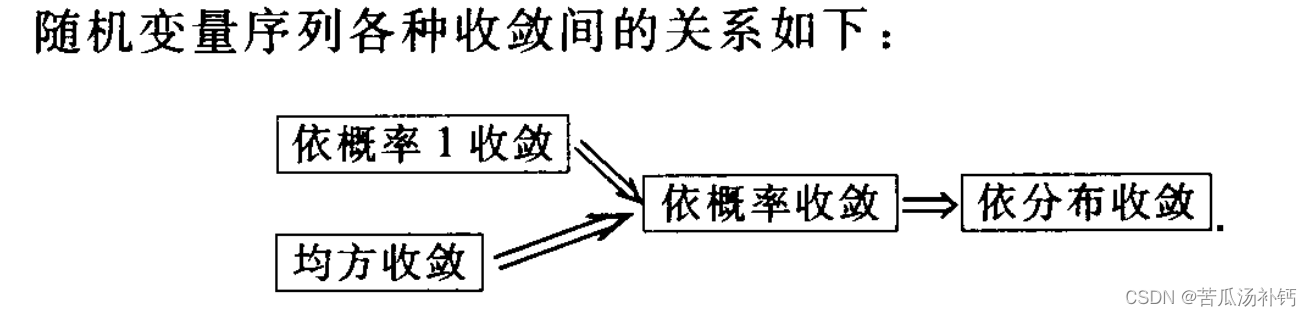
2、大数定理

3、中心极限定理

总结
以上就是今天要讲的内容,仅仅简单介绍了一些概率论的基本概念。
相关文章:

随机过程及应用学习笔记(一)概率论(概要)
概率是随机的基础,在【概率论(概要)】这个部分中仅记录学习随机过程及应用的基本定义和结果。 前言 首先,概率论研究的基础是概率空间。概率空间由一个样本空间和一个概率测度组成,样本空间包含了所有可能的结果&…...
洛谷_P1059 [NOIP2006 普及组] 明明的随机数_python写法
这道题的关键在于去重和排序,去重可以联想到集合,那排序直接使用sort方法。 n int(input()) data set(map(int,input().split( ))) data list(data) data.sort() print(len(data)) for i in data:print(i,end )...

爆火的人工智能开源open-interpreter源码解析
今天这篇文章带大家一起来阅读下github上爆火的开源项目 open-interpreter的源代码,相当于是一个可以本地部署的openai code-interpreter。 今天这期我们透过现象看本质,一起来剖析下他的源码。 体验open-interpreter的视频地址 open-interpreter&…...
)
POM设计模式思路,详解POM:概述与介绍,POM思路梳理+代码示例(全)
概述 在UI自动化测试中,POM模式是一种设计思路,它的核心思想是方法的封装。它将方法类和页面元素进行分离,增强了代码的可维护性。值得注意的是,这种分层的设计模式,最好也是从线性代码开始,逐步将代码进行…...
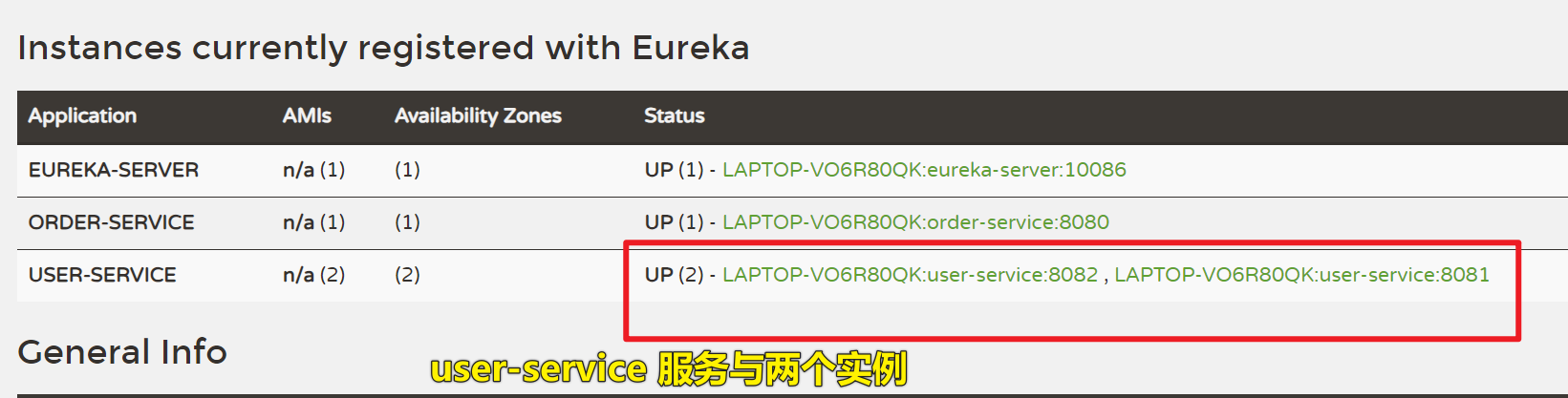
1、学习 Eureka 注册中心
学习 Eureka 注册中心 一、创建 Eureka 微服务0、SpringBoot 和 SpringCloud 版本1、引入 Eureka 服务端依赖2、启动类加 EnableEurekaServer 注解3、配置 yaml 文件,把 Eureka 服务注册到 Eureka 注册中心4、访问 Eureka 服务端,查看注册中心的服务列表…...

何为分账系统?
1、分账系统产生的背景 在数字化浪潮下第三方支付价值凸显,大大提升资金流与信息流流转效率,成为构建产业数字化重要枢纽。近年来,基于云计算、大数据、人工智能、物联网等技术积累,以第三方支付为切点的金融科技创新爆发着强大的…...
机器学习10-特征缩放
特征缩放的目的是确保不同特征的数值范围相近,使得模型在训练过程中更加稳定,加速模型收敛,提高模型性能。具体而言,零均值和单位方差的目标有以下几点好处: 1. 均值为零(Zero Mean):…...
Java基于微信小程序的医院挂号小程序,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...

HarmonyOS一杯冰美式的时间 -- 验证码框
一、前言 像是短密码、验证码都有可能需要一个输入框,像是如下: 恰好在写HarmonyOS的时候也需要写一个验证码输入框,但是在实现的时候碰了几次灰,觉得有必要分享下,故有了此篇文章。 如果您有任何疑问、对文章写的不…...

GitLab配置SSHKey
段落一:什么是SSH密钥 SSH(Secure Shell)是一种网络协议,用于安全地远程登录和执行命令。SSH密钥是一种用于身份验证的加密文件,它允许您在与远程服务器通信时,无需输入密码即可进行认证。在GitLab中配置S…...

通过QT制作一个模仿微信主界面的界面(不要求实现具体通信功能)
main.cpp #include "widget.h" #include "second.h"#include <QApplication>int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();//实例化第二个界面Second s;QObject::connect(&w, &Widget::my_jump, &…...
 数据同化思路)
作物模型狂奔:WOFOST(PCSE) 数据同化思路
去B吧,这里没图 整体思路:PCSE -》 敏感性分析 -》调参 -》同化 0、准备工作 0.0 电脑环境 我用的Win10啦,Linux、Mac可能得自己再去微调一下。 0.1 Python IDE 我用的Pycharm,个人感觉最好使的IDE,没有之一。 …...
腾讯云4核8G服务器能支持多少人访问?
腾讯云4核8G服务器支持多少人在线访问?支持25人同时访问。实际上程序效率不同支持人数在线人数不同,公网带宽也是影响4核8G服务器并发数的一大因素,假设公网带宽太小,流量直接卡在入口,4核8G配置的CPU内存也会造成计算…...

多重背包问题 ⅠⅡ Ⅲ
有 N 种物品和一个容量是 V 的背包。 第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。 输入 第一行两个整数,N…...
挑战杯 python的搜索引擎系统设计与实现
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 python的搜索引擎系统设计与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:5分创新点:3分 该项目较为新颖ÿ…...

【LeetCode: 103. 二叉树的锯齿形层序遍历 + BFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
C#学习(十三)——多线程与异步
一、什么是线程 程序执行的最小单元 一次页面的渲染、一次点击事件的触发、一次数据库的访问、一次登录操作都可以看作是一个一个的进程 在一个进程中同时启用多个线程并行操作,就叫做多线程 由CPU来自动处理 线程有运行、阻塞、就绪三态 代码示例: cl…...
)
MySQL 数据库安装教程详解(linux系统和windows系统)
MySQL 数据库是一种广泛使用的开源关系数据库管理系统。在 Linux 和 Windows 系统上安装 MySQL 数据库的步骤略有不同。以下是详细的安装教程。 Linux 系统安装教程 1. **安装前提**:确保你的 Linux 系统已经安装了 wget、unzip、tar 等必要的工具。 2. **下…...

从汇编分析C语言可变参数的原理,并实现一个简单的sprintf函数
C语言可变参数 使用printf等函数的时候函数原型是printf(const char* fmt, ...), 这一类参数的个数不限的函数是可变参数 使用 使用一个头文件stdarg.h, 主要使用以下的宏 typedef char * va_list;// 把 n 圆整到 sizeof(int) 的倍数 #define _INTSIZEOF(n) ( (sizeo…...
Word docx文件重命名为zip文件,解压后直接查看和编辑
一个不知道算不算冷的知识[doge]: docx格式的文件本质上是一个ZIP文件 当把一个.docx文件重命名为.zip文件并解压后,你会发现里面包含了一些XML文件和媒体文件,它们共同构成了Word文档的内容和格式。 例如,word/document.xml文件…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...





