多重背包问题 ⅠⅡ Ⅲ
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入
第一行两个整数,N,V,用空格隔开,分别表示物品种数和背包容积。
接下来有 N 行,每行三个整数 vi,wi,si,用空格隔开,分别表示第 i 种物品的体积、价值和数量。
输出
输出一个整数,表示最大价值。
Input
4 5
1 2 3
2 4 1
3 4 3
4 5 2
Output
10
根据不同的数据范围,有不同的选择
Ⅰ. 数据范围 0<N,V≤100 0<vi,wi,si≤100
直接写
//代码一
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=510,M=6010;
int n,m;
int v,w,s;
int f[N][M];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){cin>>v>>w>>s;for (int j=1;j<=m;j++)for (int k=0;k<=s&&k*v<=j;k++)f[i][j]=max(f[i][j],f[i-1][j-k*v]+k*w);}cout<<f[n][m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}//代码二:降一维
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=510,M=6010;
int n,m;
int v,w,s;
int f[M];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){cin>>v>>w>>s;for (int j=m;j>=v;j--)for (int k=0;k<=s&&k*v<=j;k++)f[j]=max(f[j],f[j-k*v]+k*w);}cout<<f[m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}Ⅱ. 数据范围 0<N≤1000,0<V≤2000,0<vi,wi,si≤2000
通过二进制将每种物品按照个数的不同重新打包,再按01背包的方式选择
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=1e6+10;
int n,m;
int f[N],v[N],w[N];
int cnt;
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){int a,b,s;cin>>a>>b>>s;int k=1;while (k<=s){cnt++;v[cnt]=k*a;w[cnt]=k*b;s -=k;k *=2;}if (s>0){cnt++;v[cnt]=s*a;w[cnt]=s*b;}}for (int i=1;i<=cnt;i++)for (int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);cout<<f[m];
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}Ⅲ. 数据范围 0<N≤1000,0<V≤20000,0<vi,wi,si≤20000
通过单调队列来更新状态
//代码一
#include <bits/stdc++.h>
using namespace std;
//#define int long long //不开就不开吧
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=1010,M=2e4+10;
int n,m;
int f[N][M],q[M];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){int v,w,s;cin>>v>>w>>s;for (int j=0;j<v;j++){int hh=0,tt=-1;for (int k=j;k<=m;k +=v){if (hh<=tt&&k-q[hh]>s*v) hh++; //判断队头是否滑出窗口,队列中的v不能超过上限s个while (hh<=tt&&f[i-1][q[tt]]-(q[tt]-j)/v*w<=f[i-1][k]-(k-j)/v*w) tt--;q[++tt]=k;f[i][k]=f[i-1][q[hh]]+(k-q[hh])/v*w;}}}cout<<f[n][m];
}
int main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}//代码二 降一维
#include <bits/stdc++.h>
using namespace std;
//#define int long long //不开就不开吧
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e4+10;
int n,m;
int f[N],g[N],q[N];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++){int v,w,s;cin>>v>>w>>s;memcpy(g,f,sizeof f); //滚动数组,备份上一次的状态for (int j=0;j<v;j++){int hh=0,tt=-1;for (int k=j;k<=m;k +=v){if (hh<=tt&&k-q[hh]>s*v) hh++; //判断队头是否滑出窗口,队列中的v不能超过上限s个while (hh<=tt&&g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w) tt--;q[++tt]=k;f[k]=g[q[hh]]+(k-q[hh])/v*w;}}}cout<<f[m];
}
int main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}相关文章:

多重背包问题 ⅠⅡ Ⅲ
有 N 种物品和一个容量是 V 的背包。 第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。 求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。 输出最大价值。 输入 第一行两个整数,N…...
挑战杯 python的搜索引擎系统设计与实现
0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 python的搜索引擎系统设计与实现 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:5分创新点:3分 该项目较为新颖ÿ…...

【LeetCode: 103. 二叉树的锯齿形层序遍历 + BFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
C#学习(十三)——多线程与异步
一、什么是线程 程序执行的最小单元 一次页面的渲染、一次点击事件的触发、一次数据库的访问、一次登录操作都可以看作是一个一个的进程 在一个进程中同时启用多个线程并行操作,就叫做多线程 由CPU来自动处理 线程有运行、阻塞、就绪三态 代码示例: cl…...
)
MySQL 数据库安装教程详解(linux系统和windows系统)
MySQL 数据库是一种广泛使用的开源关系数据库管理系统。在 Linux 和 Windows 系统上安装 MySQL 数据库的步骤略有不同。以下是详细的安装教程。 Linux 系统安装教程 1. **安装前提**:确保你的 Linux 系统已经安装了 wget、unzip、tar 等必要的工具。 2. **下…...

从汇编分析C语言可变参数的原理,并实现一个简单的sprintf函数
C语言可变参数 使用printf等函数的时候函数原型是printf(const char* fmt, ...), 这一类参数的个数不限的函数是可变参数 使用 使用一个头文件stdarg.h, 主要使用以下的宏 typedef char * va_list;// 把 n 圆整到 sizeof(int) 的倍数 #define _INTSIZEOF(n) ( (sizeo…...
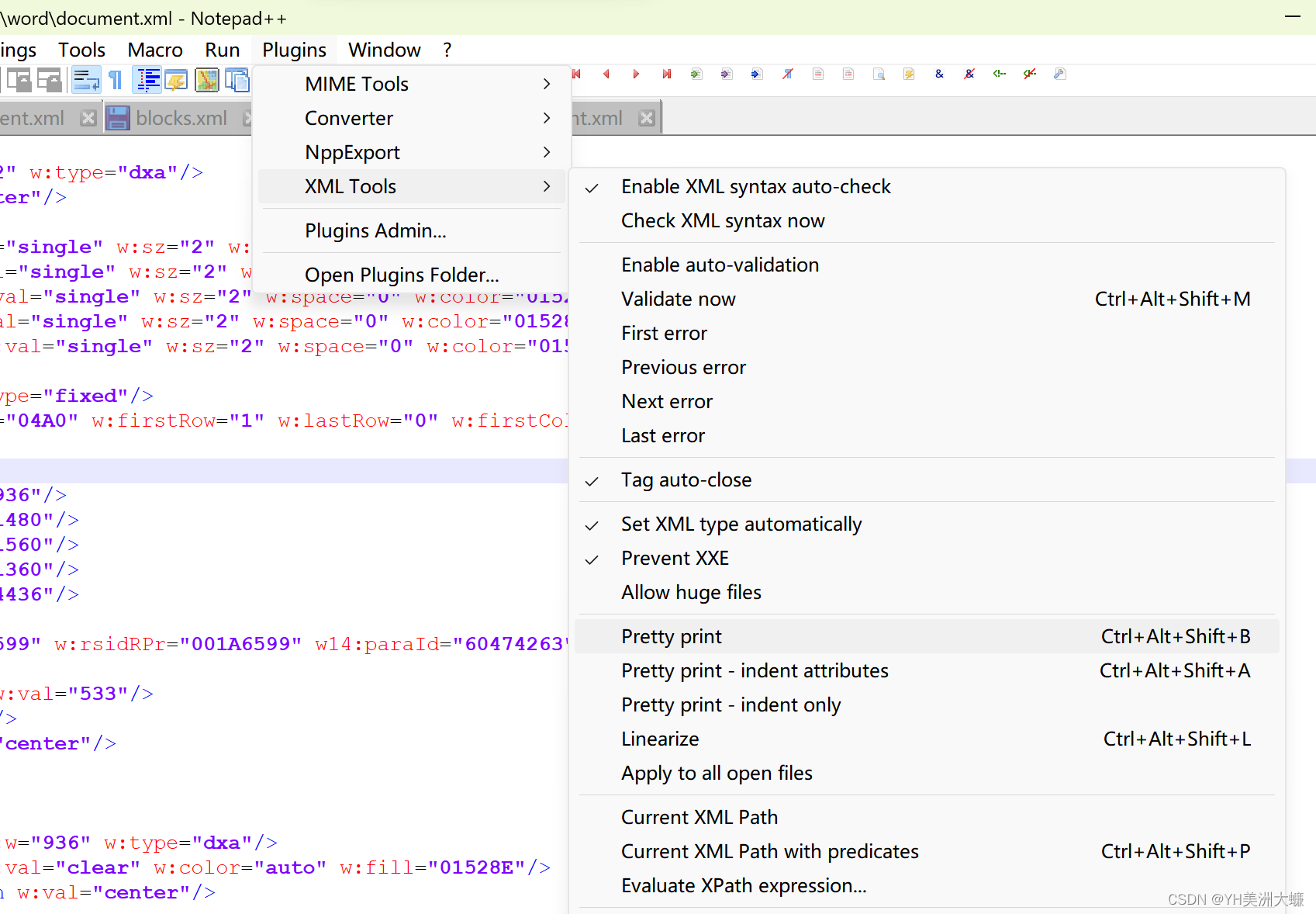
Word docx文件重命名为zip文件,解压后直接查看和编辑
一个不知道算不算冷的知识[doge]: docx格式的文件本质上是一个ZIP文件 当把一个.docx文件重命名为.zip文件并解压后,你会发现里面包含了一些XML文件和媒体文件,它们共同构成了Word文档的内容和格式。 例如,word/document.xml文件…...

SpringBoot中公共字段的自动填充
目录 1 前言 2 使用方法 2.1 自定义枚举类 2.2 自定义注解AutoFill 2.3 自定义切面类并设定切入点 2.4 切面类中设置前置通知,对公共字段赋值 2.5 在方法上添加自定义注解 3 最后 1 前言 在我们的项目中,项目表可能会有一些公共的字段需要我们的…...

【天衍系列 03】深入理解Flink的Watermark:实时流处理的时间概念与乱序处理
文章目录 01 基本概念02 工作原理03 优势与劣势04 核心组件05 Watermark 生成器 使用06 应用场景07 注意事项08 案例分析8.1 窗口统计数据不准8.2 水印是如何解决延迟与乱序问题?8.3 详细分析 09 项目实战demo9.1 pom依赖9.2 log4j2.properties配置9.3 Watermark水印…...

day07.C++类与对象
一.类与对象的思想 1.1面向对象的特点 封装、继承、多态 1.2类的概念 创建对象的过程也叫类的实例化。每个对象都是类的一个具体实例(Instance),拥有类的成员变量和成员函数。由{ }包围,由;结束。 class name{ //类的…...
String讲解
文章目录 String类的重要性常用的方法常用的构造方法String类的比较字符串的查找转化数字转化为字符串字符串转数字 字符串替换字符串的不可变性 字符串拆分字符串截取字符串修改 StringBuilder和StringBuffer String类的重要性 在c/c的学习中我们接触到了字符串,但…...

人群异常聚集监测系统-聚众行为检测与识别算法---豌豆云
聚众识别系统对指定区域进行实时监测,当监测到人群大量聚集、达到设置上限时,立即告警及时疏散。 旅游业作为国民经济战略性支柱产业,随着客流量不断增加,旅游景区和一些旅游城市的管理和服务面临着前所未有的挑战: …...
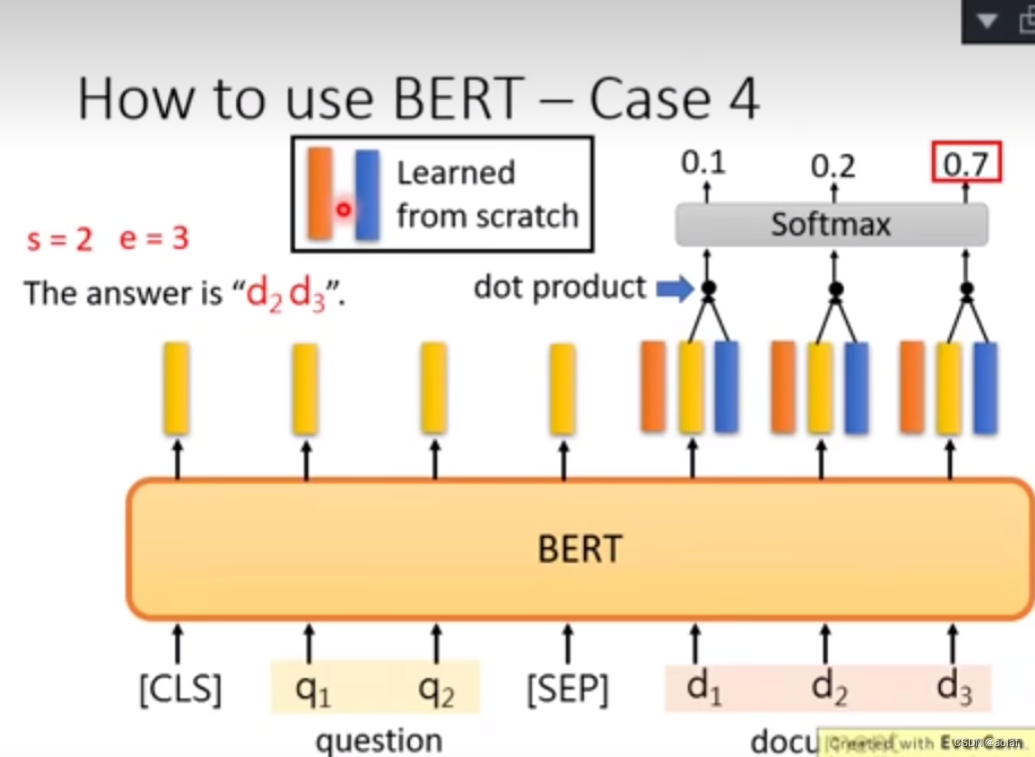
多模态基础---BERT
1. BERT简介 BERT用于将一个输入的句子转换为word_embedding,本质上是多个Transformer的Encoder堆叠在一起。 其中单个Transformer Encoder结构如下: BERT-Base采用了12个Transformer Encoder。 BERT-large采用了24个Transformer Encoder。 2. BERT的…...

图表示学习 Graph Representation Learning chapter2 背景知识和传统方法
图表示学习 Graph Representation Learning chapter2 背景知识和传统方法 2.1 图统计和核方法2.1.1 节点层次的统计和特征节点的度 节点中心度聚类系数Closed Triangles, Ego Graphs, and Motifs 图层次的特征和图的核节点袋Weisfieler–Lehman核Graphlets和基于路径的方法 邻域…...
)
OpenMVG(计算两个球形图像之间的相对姿态、细化重建效果)
目录 1 Bundle Adjustment(细化重建效果) 2 计算两个球形图像之间的相对姿态 1 Bundle Adjustment(细化重建效果) 数...
)
【QT+QGIS跨平台编译】之三十四:【Pixman+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、Pixman介绍二、文件下载三、文件分析四、pro文件五、编译实践一、Pixman介绍 Pixman是一款开源的软件库,提供了高质量的像素级图形处理功能。它主要用于在图形渲染、合成和转换方面进行优化,可以帮助开发人员在应用程序中实现高效的图形处理。 Pixman的主要特…...

2.17学习总结
tarjan 【模板】缩点https://www.luogu.com.cn/problem/P3387 题目描述 给定一个 �n 个点 �m 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。 允许多次经过一条边或者…...

Unity类银河恶魔城学习记录7-7 P73 Setting sword type源代码
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Sword_Skill_Controller.cs using System.Collections; using System.Col…...
安卓版本与鸿蒙不再兼容,鸿蒙开发工程师招疯抢
最近,互联网大厂纷纷开始急招华为鸿蒙开发工程师。这是一个新的信号。在Android和iOS长期霸占市场的今天,鸿蒙的崛起无疑为整个行业带来了巨大的震动。 2023年11月10日,网易更新了高级/资深Android开发工程师岗位,职位要求参与云音…...
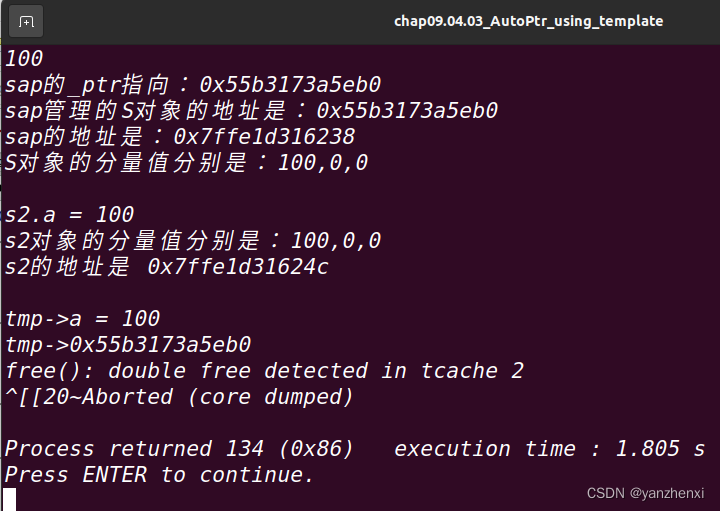
《白话C++》第9章 泛型,Page842~844 9.4.2 AutoPtr
源起: C编程中,最容易出的问题之一,就是内存泄露,而new一个对象,却忘了delete它,则是造成内存泄露的主要原因之一 例子一: void foo() {XXXObject* xo new XXXObject;if(!xo->DoSomethin…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...
