图表示学习 Graph Representation Learning chapter2 背景知识和传统方法
图表示学习 Graph Representation Learning chapter2 背景知识和传统方法
- 2.1 图统计和核方法
- 2.1.1 节点层次的统计和特征
- 节点的度
- 节点中心度
- 聚类系数
- Closed Triangles, Ego Graphs, and Motifs
- 图层次的特征和图的核
- 节点袋
- Weisfieler–Lehman核
- Graphlets和基于路径的方法
- 邻域重叠检测
2.1 图统计和核方法
2.1.1 节点层次的统计和特征
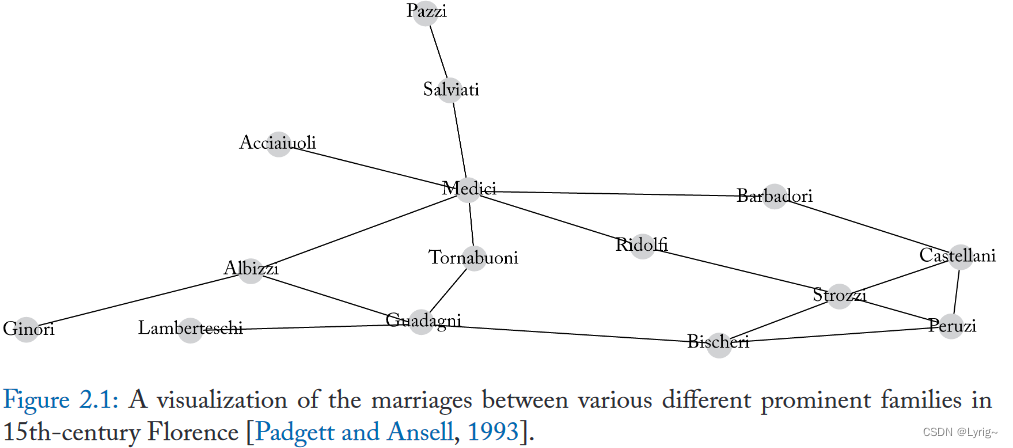
节点的度
d u = ∑ v ∈ V A ( u , v ) (2.1) d_u = \sum_{v\in \mathcal{V}} A(u, v)\tag{2.1} du=v∈V∑A(u,v)(2.1)
需要说明的是,在有向和加权图中,度可以区分为不同的概念。例如入度和出度之类的。不管怎么说,这个特征在传统机器学习中都是十分重要的。
节点中心度
e u = 1 λ ∑ v ∈ V A ( u , v ) e v , ∀ u ∈ V (2.2) e_u = \frac{1}{\lambda}\sum_{v\in \mathcal{V}}A(u, v)e_v, \forall u\in \mathcal{V}\tag{2.2} eu=λ1v∈V∑A(u,v)ev,∀u∈V(2.2)
一种常见的方式是利用特征向量中心度,我们定义每个节点的中心度为周围所有中心度的均值,其中 λ \lambda λ是一个常数。
求解这一过程,可以写作如下形式: λ e = A e (2.3) \lambda e = Ae\tag{2.3} λe=Ae(2.3)
如果我们期望所有的中心度都是正的,我们可以应用Perron-Frobenius Theorem,即对A求解特征向量。
此外我们也可以通过迭代法如下: e ( t + 1 ) = A e ( t ) (2.4) e^{(t+1)}=Ae^{(t)}\tag{2.4} e(t+1)=Ae(t)(2.4)
如果我们设 e 0 = ( 1 , 1 , . . . , 1 ) T e^0=(1,1,...,1)^T e0=(1,1,...,1)T那么每次迭代后的结果是截至T步时,经过的次数,由此可以得到重要性。
聚类系数
用于衡量节点局部邻域封闭三角形的比例。
c u = ∣ ( v 1 , v 2 ) ∈ E : v 1 , v 2 ∈ N ( u ) ∣ C d u 2 (2.5) c_u=\frac{|(v_1,v_2)\in \mathcal{E}:v_1,v_2\in \mathcal{N}(u)|}{C_{d_u}^2}\tag{2.5} cu=Cdu2∣(v1,v2)∈E:v1,v2∈N(u)∣(2.5)
其中 N ( u ) = { v ∈ V : ( u , v ) ∈ E } \mathcal{N}(u)=\{v\in \mathcal{V}:(u,v)\in \mathcal{E}\} N(u)={v∈V:(u,v)∈E}也就是所有的相邻节点构成的集合。
这一特征描述了节点附近结构的紧密程度。
Closed Triangles, Ego Graphs, and Motifs
略
图层次的特征和图的核
节点袋
单纯综合节点的特征。
Weisfieler–Lehman核
一种迭代邻域聚合方法。

Graphlets和基于路径的方法
Graphlets:计算不同子图结构出现次数。具体方式为,枚举所有可能的子图结构,然后统计出现的次数。
基于路径,则是统计类似于最短路之类的。
邻域重叠检测
未完待续。
相关文章:

图表示学习 Graph Representation Learning chapter2 背景知识和传统方法
图表示学习 Graph Representation Learning chapter2 背景知识和传统方法 2.1 图统计和核方法2.1.1 节点层次的统计和特征节点的度 节点中心度聚类系数Closed Triangles, Ego Graphs, and Motifs 图层次的特征和图的核节点袋Weisfieler–Lehman核Graphlets和基于路径的方法 邻域…...
)
OpenMVG(计算两个球形图像之间的相对姿态、细化重建效果)
目录 1 Bundle Adjustment(细化重建效果) 2 计算两个球形图像之间的相对姿态 1 Bundle Adjustment(细化重建效果) 数...
)
【QT+QGIS跨平台编译】之三十四:【Pixman+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、Pixman介绍二、文件下载三、文件分析四、pro文件五、编译实践一、Pixman介绍 Pixman是一款开源的软件库,提供了高质量的像素级图形处理功能。它主要用于在图形渲染、合成和转换方面进行优化,可以帮助开发人员在应用程序中实现高效的图形处理。 Pixman的主要特…...

2.17学习总结
tarjan 【模板】缩点https://www.luogu.com.cn/problem/P3387 题目描述 给定一个 �n 个点 �m 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。 允许多次经过一条边或者…...

Unity类银河恶魔城学习记录7-7 P73 Setting sword type源代码
Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释,可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Sword_Skill_Controller.cs using System.Collections; using System.Col…...
安卓版本与鸿蒙不再兼容,鸿蒙开发工程师招疯抢
最近,互联网大厂纷纷开始急招华为鸿蒙开发工程师。这是一个新的信号。在Android和iOS长期霸占市场的今天,鸿蒙的崛起无疑为整个行业带来了巨大的震动。 2023年11月10日,网易更新了高级/资深Android开发工程师岗位,职位要求参与云音…...
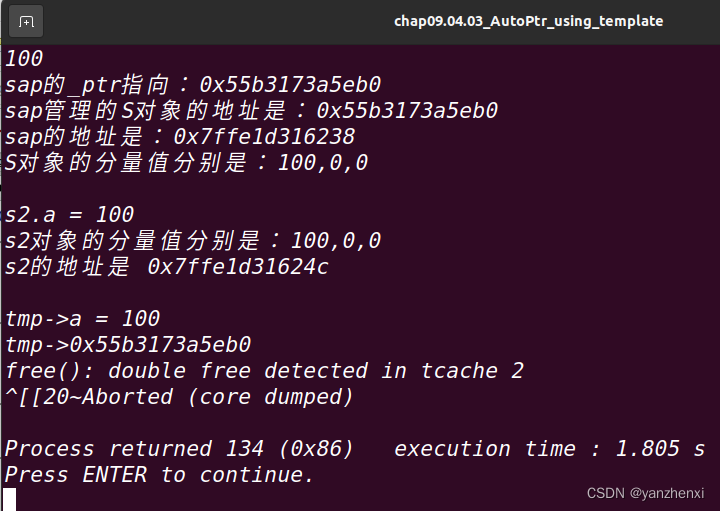
《白话C++》第9章 泛型,Page842~844 9.4.2 AutoPtr
源起: C编程中,最容易出的问题之一,就是内存泄露,而new一个对象,却忘了delete它,则是造成内存泄露的主要原因之一 例子一: void foo() {XXXObject* xo new XXXObject;if(!xo->DoSomethin…...
服务流控(Sentinel)
引入依赖 <!-- 必须的 --> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId> </dependency><!-- sentinel 核心库 --> <dependency><groupId>com.ali…...

点亮代码之灯,程序员的夜与电脑
在科技的海洋里,程序员是那些驾驶着代码船只,穿梭于虚拟世界的探险家。他们手中的键盘是航行的舵,而那台始终不愿关闭的电脑,便是他们眼中永不熄灭的灯塔。有人说,程序员不喜欢关电脑,这究竟是为什么呢&…...

ClickHouse--07--Integration 系列表引擎
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 Integration 系列表引擎1 HDFS1.1 语法1.2 示例: 2 MySQL2.1 语法2.2 示例: 3 Kafka3.1 语法3.2 示例:3.3 数据持久化方法 Integ…...

前端架构: 脚手架框架之yargs的11种基础核心特性的应用教程
脚手架框架之yargs的基础核心特性与应用 1 )概述 yargs 是脚手架当中使用量非常大的一个框架进入它的npm官网: https://www.npmjs.com/package/yargs 目前版本: 17.7.2Weekly Downloads: 71,574,188 (动态数据)最近更新:last month (github)说明这是一个…...
-主从复制的配置与管理)
MySQL性能调优篇(6)-主从复制的配置与管理
MySQL数据库主从复制是一种常用的数据复制和高可用性解决方案。它允许将一个MySQL主服务器上的数据自动复制到多个从服务器上,从而提供了数据冗余备份、读写分离等优势。本文将详细介绍MySQL数据库主从复制的配置与管理。 1. 原理概述 MySQL主从复制是基于二进制日…...
Linux第49步_移植ST公司的linux内核第1步_获取linux源码
已知ST公司的linux源码路径: /home/zgq/linux/atk-mp1/stm32mp1-openstlinux-5.4-dunfell-mp1-20-06-24/sources/arm-ostl-linux-gnueabi/linux-stm32mp-5.4.31-r0 1、创建“my_linux”目录 打开第1个终端 输入“ls回车” 输入“cd linux/回车”,切换…...

怎样学习Windows下命令行编写
第一:Windows下命令行指的是cmd和powershell命令行编写 第二:必须要用好help或/?命令,这个命令是最基本的也是最常用的命令列表和语法查看命令 第三:cmd命令使用help查看命令列表或“一串带参数的命令 /?"(不…...
数据结构第十六天(二叉树层序遍历/广度优先搜索(BFS)/队列使用)
目录 前言 概述 接口 源码 测试函数 运行结果 往期精彩内容 前言 从前的日色变得慢,车,马,邮件都慢,一生,只够爱一个人。 概述 二叉树的层序遍历可以使用广度优先搜索(BFS)来实现。具体步骤如下&…...
Networking)
6.s081 学习实验记录(八)Networking
文章目录 network driver network driver //TODO...

图解贝塞尔曲线生成原理
贝塞尔曲线是一种在计算机图形学中广泛使用的参数曲线,主要用于二维图形应用程序中。它是由法国工程师皮埃尔贝塞尔在1962年提出的,主要用于汽车车身设计。贝塞尔曲线的主要特点是,只要确定了控制点,就可以生成一条平滑的曲线。 …...

租房招聘|在线租房和招聘平台|基于Springboot的在线租房和招聘平台设计与实现(源码+数据库+文档)
在线租房和招聘平台目录 目录 基于Springboot的在线租房和招聘平台设计与实现 一、前言 二、系统功能设计 三、系统实现 1、房屋管理 2、招聘管理 3、平台资讯管理 4、平台资讯类型管理 四、数据库设计 1、实体ER图 六、论文参考 七、最新计算机毕设选题推荐 八、源…...

简单试验:用Excel进行爬虫
文章目录 Excel的版本具体操作实例从网站上爬取工商银行的汇率Excel的版本 office 2016,2019,365这几个版本都可以 具体操作 #mermaid-svg-NlIVMivGoJbdyWW0 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-NlIVMi…...

SQL 精讲-MySql 常用函数,MySQL语句精讲和举例
FORMAT(数值,保留位数) 四舍五入 SELECT *,FORMAT(score/3,2) from studentROUND(数值,保留位数) 四舍五入 SELECT ROUND(score/3,2) from studentCONCAT(字符串 1,字符串 2) 字符串拼接 SELECT CONCAT(customer_name, (,address,)) from mt_customerLEFT(字符串,长度) 截取…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
