二分、快排、堆排与双指针
二分
int Binary_Search(vector<int> A,int key){int n=A.size();int low=0,high=n-1,mid;while(low<=high){mid=(low+high)/2;if(A[mid]==key)return mid;else if(A[mid]>key)high=mid-1;elselow=mid+1; }return -1;
}
折半插入排序
——找到第一个 ≥ \ge ≥tem的元素
void InsertSort(vector<int> A){int n=A.size();int low,high,mid;for(int i=1;i<=n;i++){int tem=A[i];low=1;high=i-1;while(low<=high){mid=(low+high)/2;if(A[mid]>tem) //只要A[high]>tem,就不断往后移high=mid-1; else //先往右移,后续往做移low=mid+1;}for(int j=i-1;j>=high+1;j--)A[j+1]=A[j];A[high+1]=tem;}
在非递减数组中找到比x小的最后一个元素和比x大的第一个元素
- 每次有要处理的就if-else
- 为了避免无限循环>>[begin,mid-1] U mid U [mid+1,end]
- 为了产生mid+1对nums[mid+1]进行讨论
class Solution {
public:int search_left(vector<int> nums,int begin,int end,int target){if(begin>end) return -1;if(nums[end]<target)return end;if(nums[begin]>=target)return begin-1;else {int mid=(begin+end)/2;if(nums[mid]>=target)return search_left(nums,begin,mid-1,target);else {if(mid==nums.size()-1)return -1;else if(nums[mid+1]>=target)return mid;else return search_left(nums,mid+1,end,target);}}}int search_right(vector<int> nums,int begin,int end,int target){if(begin>end) return nums.size();if(nums[begin]>target){return begin;} if(nums[end]<=target){return end+1;}else {int mid=(begin+end)/2;if(nums[mid]<=target)return search_right(nums,mid+1,end,target);else{if(mid==0) return nums.size();if(nums[mid-1]<=target) return mid;else return search_right(nums,begin,mid-1,target);}}}vector<int> searchRange(vector<int>& nums, int target) {int N=nums.size();int left=search_left(nums,0,N-1,target);int right=search_right(nums,0,N-1,target);vector<int> ans(2);if(left>=right-1){ans[0]=-1; ans[1]=-1;}else {ans[0]=left+1;···ans[1]=right-1;} return ans; }
};
三数之和
- 三数之和首先把nums[0]~nums[n-1]排序
- 在a固定的情形下,条件: 每次c及其右侧所有可能都被确定,
利用贪心性质:if b+c+a<0, b左侧的在c往左移的过程中更不可能,因此b++
else if b+c+a>0,c及其右侧在b右移的过程中更不可能,因此c–,
b+c+a=0,当前的b及其左侧已不可能,不妨b++,
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();sort(nums.begin(), nums.end());vector<vector<int>> ans;// 枚举 afor (int first = 0; first < n; ++first) {// 需要和上一次枚举的数不相同if (first > 0 && nums[first] == nums[first - 1]) {continue;}// c 对应的指针初始指向数组的最右端int third = n - 1;int target = -nums[first];// 枚举 bfor (int second = first + 1; second < n; ++second) {// 需要和上一次枚举的数不相同if (second > first + 1 && nums[second] == nums[second - 1]) {continue;}// 需要保证 b 的指针在 c 的指针的左侧while (second < third && nums[second] + nums[third] > target) {--third;}// 如果指针重合,随着 b 后续的增加// 就不会有满足 a+b+c=0 并且 b<c 的 c 了,可以退出循环if (second == third) {break;}if (nums[second] + nums[third] == target) {ans.push_back({nums[first], nums[second], nums[third]});}}}return ans;}
};`
四数相加
- 要返回解,只能2层循环+双指针,2个数组的双指针,不能输出全部解
class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {unordered_map<int,int>hash;int res = 0;int n =nums1.size();for(int i=0;i<n;i++){for(int j=0;j<n;j++){hash[nums1[i]+nums2[j]]++;}} for(int i=0;i<n;i++){for(int j=0;j<n;j++){auto it = hash.find(-(nums3[i]+nums4[j]));if(it!=hash.end()){res += it->second;}}}return res;}
};
滑动窗口最大值
mean1: priority_queue
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {auto cmp = [](const pair<int, int>& a, const pair<int, int>& b) -> bool { return a.first < b.first; };priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> pq(cmp);int n=nums.size();vector<int> ans;for(int i=0;i<n;i++){pq.push({nums[i],i});while(pq.top().second<i-k+1){pq.pop();}if(i>=k-1)ans.push_back(pq.top().first);}return ans;}
};
mean2: 单调队列
deque=双端队列,有clear()
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {int n = nums.size();deque<int> q;for (int i = 0; i < k; ++i) {while (!q.empty() && nums[i] >= nums[q.back()]) {q.pop_back();}q.push_back(i);}vector<int> ans = {nums[q.front()]};for (int i = k; i < n; ++i) {while (!q.empty() && nums[i] >= nums[q.back()]) {q.pop_back();}q.push_back(i);while (q.front() <= i - k) {q.pop_front();}ans.push_back(nums[q.front()]);}return ans;}
};
Exp++
- 本质是用堆化简排序
双指针
for (int i = 0, j = 0; i < n; i ++ ) // j从某一位置开始,不一定是0
{while (j < i && check(i, j)) j ++ ;// 具体问题的逻辑
}
常见问题分类:(1) 对于一个序列,用两个指针维护一段区间,比如快排的划分过程(2) 对于两个序列,维护某种次序,比如归并排序中合并两个有序序列的操作
- 双指针算法的核心思想(作用):优化.
- 在利用双指针算法解题时,考虑原问题如何用暴力算法解出,观察是否可构成单调性,若可以,就可采用双指针算法对暴力算法进行优化.
- 当我们采用朴素的方法即暴力枚举每一种可能的情况,时间复杂度为O(n*n),双指针降为O(n).
相关文章:

二分、快排、堆排与双指针
二分 int Binary_Search(vector<int> A,int key){int nA.size();int low0,highn-1,mid;while(low<high){mid(lowhigh)/2;if(A[mid]key)return mid;else if(A[mid]>key)highmid-1;elselowmid1; }return -1; }折半插入排序 ——找到第一个 ≥ \ge ≥tem的元素 voi…...

微信小程序步数返还的时间戳为什么返回的全是1970?
微信小程序步数返还的时间戳为什么返回的全是1970? 将返回的时间 乘以 1000 再 new Date() 转化就对了 微信返回的是秒S单位的,我们要转化为毫秒ms单位,才能进行格式化日期。 微信给我们下了个坑, 参考: https://d…...

Python函数——函数介绍
一、引言 在Python编程中,函数是构建高效代码的关键。通过创建可重用的代码块,我们可以使程序更加清晰、易读且易于维护。在本文中,我们将深入了解Python函数的基本概念及其特性。 二、Python函数的基本概念 函数是一段具有特定功能的代码块…...
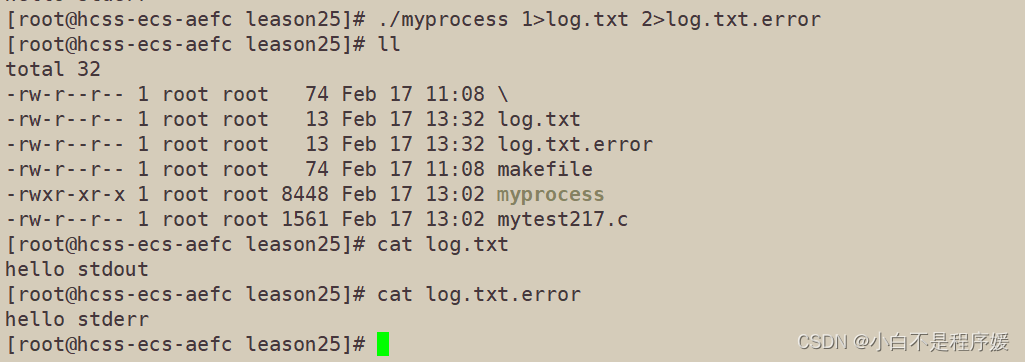
【Linux系统化学习】文件重定向
目录 文件内核对象 文件描述符的分配规则 重定向 重定向的概念 dup2系统调用 输出重定向 追加重定向 输入重定向 stderr解析 重定向到同一个文件中 分离常规输出和错输出 文件内核对象 上篇文章中我们介绍到了操作系统中的文件,操作系统为了方…...

防火墙工作模式详解
防火墙工作模式是指防火墙在网络中的工作方式和策略。常见的防火墙工作模式包括以下几种: 1. 包过滤工作模式:根据事先确定的规则集合,对进出网络的网络包进行过滤和检查。根据规则,防火墙可以允许或阻止特定的网络流量。 2. 代…...

CCF编程能力等级认证GESP—C++6级—20231209
CCF编程能力等级认证GESP—C6级—20231209 单选题(每题 2 分,共 30 分)判断题(每题 2 分,共 20 分)编程题 (每题 25 分,共 50 分)闯关游戏工作沟通 答案及解析单选题判断题编程题1编程题2 单选题…...
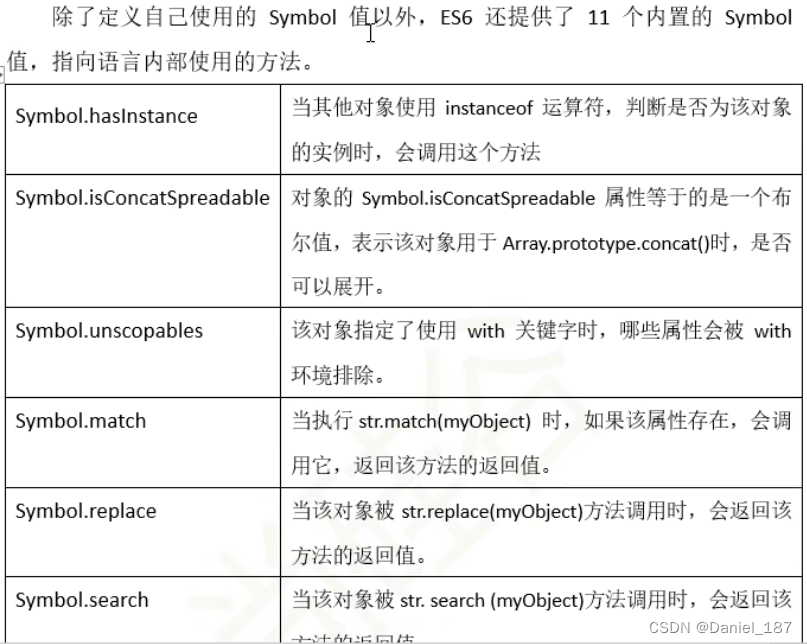
ES6 ~ ES11 学习笔记
课程地址 ES6 let let 不能重复声明变量(var 可以) let a; let b, c, d; let e 100; let f 521, g "atguigu", h [];let 具有块级作用域,内层变量外层无法访问 let 不存在变量提升(运行前收集变量和函数&#…...
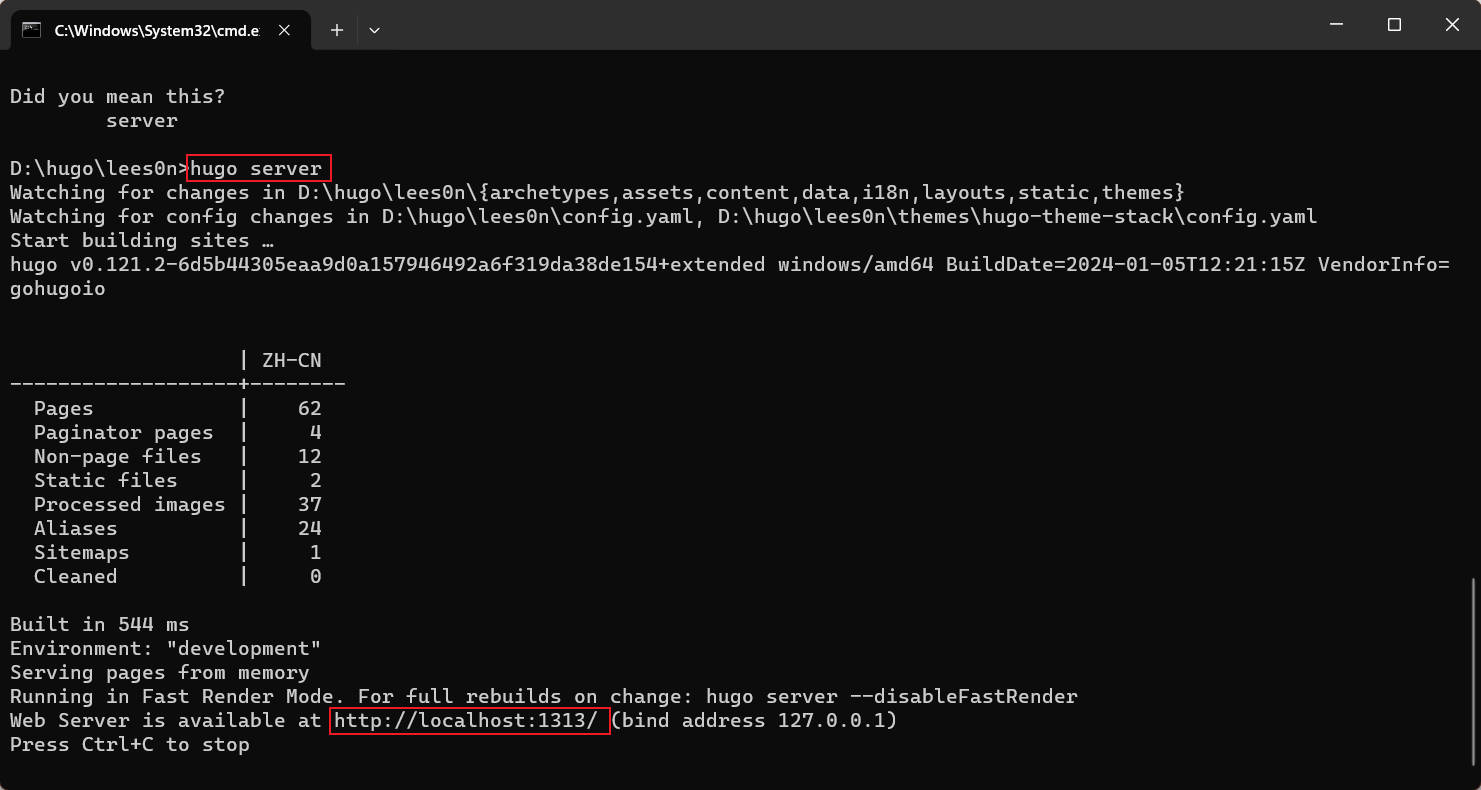
001 - Hugo, 创建一个网站
001 - Hugo, 创建一个网站安装hugoWindows系统Macos Hugo博客搭建初始化博客主题安装配置博客各个页面开始创作创建 GitHub Page 仓库本地调试和预览发布内容 教程及鸣谢文字教程视频教程 001 - Hugo, 创建一个网站 这篇文章假设你已经: 了解基本的终端命令行知识&…...

前端开发:Vue框架与前端部署
Vue Vue是一套前端框架,免除原生)avaScript中的DOM操作,简化书写。是基于MVVM(Model–View-ViewModel)思想,实现数据的双向绑定,将编程的关注点放在数据上。简单来说,就是数据变化的时候, 页面会自动刷新, 页面变化的时…...

【leetcode】深搜、暴搜、回溯、剪枝(C++)3
深搜、暴搜、回溯、剪枝(C)3 一、解数独1、题目描述2、代码3、解析 二、单词搜索1、题目描述2、代码3、解析 三、黄金矿工1、题目描述2、代码3、解析 四、不同路径III1、题目描述2、代码3、解析 一、解数独 1、题目描述 leetcode链接 2、代码 class…...

社区养老|社区养老服务系统|基于springboot社区养老服务系统设计与实现(源码+数据库+文档)
社区养老服务系统目录 目录 基于springboot社区养老服务系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、管理员部分功能 (1) 用户管理 (2)服务种类管理 (3)社区服务管理 (…...
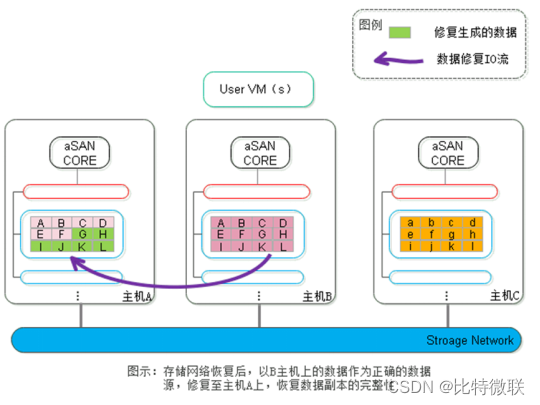
云计算基础-存储虚拟化(深信服aSAN分布式存储)
什么是存储虚拟化 分布式存储是利用虚拟化技术 “池化”集群存储卷内通用X86服务器中的本地硬盘,实现服务器存储资源的统一整合、管理及调度,最终向上层提供NFS、ISCSI存储接口,供虚拟机根据自身的存储需求自由分配使用资源池中的存储空间。…...
数学实验第三版(主编:李继成 赵小艳)课后练习答案(十二)(3)
实验十二:微分方程模型 练习三 1.分别用数值解命令ode23t和ode45 计算示例3中微分方程的数值解,同用命令ode23 算得的数值解以及解析解比较,哪种方法精度较高?你用什么方法比较它们之间的精度? clc;clear; f(x,y)2*yx2; figure(1) [x,y]ode23t(f,[1,2],1); plo…...

CSS Transition:为网页元素增添优雅过渡效果
随着互联网的发展,网页的视觉效果和用户体验变得尤为重要。CSS Transition作为一种能够让网页元素在状态改变时呈现平滑过渡效果的工具,受到了广大前端开发者的青睐。本文将详细介绍CSS Transition的基本概念、使用方法以及常见应用,帮助读者…...
)
JDK 17 新特性 (一)
既然 Springboot 3.0 强制使用 JDK 17 那就看看 JDK17 有哪些新特性吧 参考链接 介绍一下 新特性的历史渊源 JDK 17是Java Development Kit(JDK)的一个版本,它是Java编程语言的一种实现。JDK 17于2021年9月14日发布,并作为Java …...
杨中科 ASP.NET DI综合案例
综合案例1 需求说明 1、目的:演示DI的能力; 2、有配置服务、日志服务,然后再开发一个邮件发送器服务。可以通过配置服务来从文件、环境变量、数据库等地方读取配置,可以通过日志服务来将程序运行过程中的日志信息写入文件、控制台、数据库等。 3、说明…...

蓝桥杯嵌入式第12届真题(完成) STM32G431
蓝桥杯嵌入式第12届真题(完成) STM32G431 题目 程序 main.c /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief : Main program body**************************…...
)
C#系列-多线程(4)
在C#中,多线程编程主要涉及使用System.Threading命名空间下的类和接口来创建和管理线程。以下是一些C#多线程编程的基本用法和示例: 1. 使用Thread类创建线程 csharp代码 using System; using System.Threading; class Program { static void …...
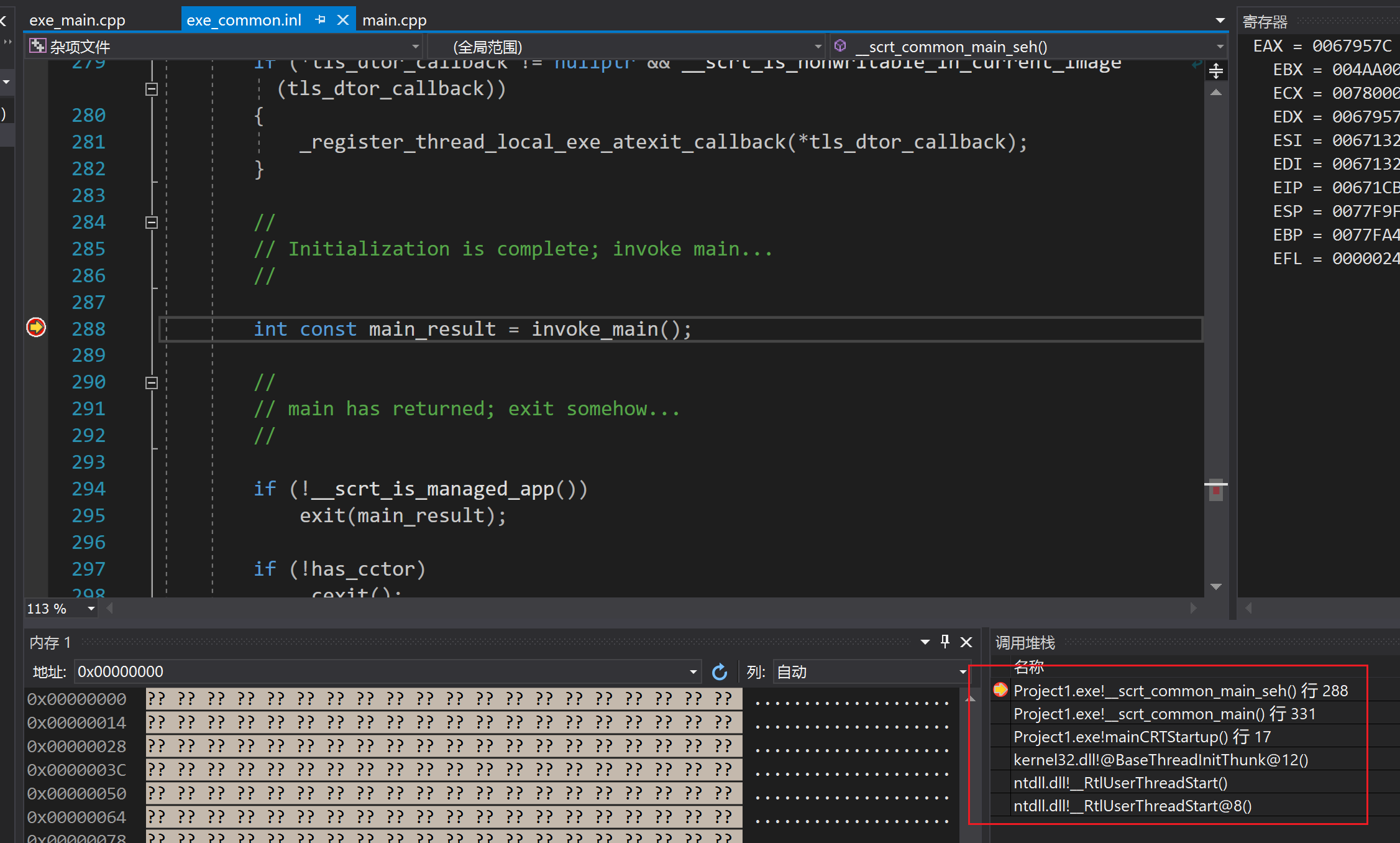
VS如何调试C运行时库
C运行时库(简称crt)是C标准库等组件的基础, 其会在进入main函数之前运行一些代码, 包括但不限于初始化堆栈, 内存分配等操作 这些代码是可以随着VC工具集一起安装到我们本地的。看一下这个情况, 就是VS调试器没找到对应的crt源码的情况, 调用堆栈是空的。为了解决这个问…...

软件工程师,超过35岁怎么办
概述 随着科技行业的飞速发展,软件开发工程师的职业道路充满了各种机遇和挑战。对于已经在这个行业摸爬滚打了十多年的软件开发工程师来说,当他们步入35岁这个年纪时,可能会感到一些迷茫和焦虑。许多人担忧,在以创新、活力、快速迭…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
