数学实验第三版(主编:李继成 赵小艳)课后练习答案(十二)(3)
实验十二:微分方程模型
练习三
1.分别用数值解命令ode23t和ode45 计算示例3中微分方程的数值解,同用命令ode23 算得的数值解以及解析解比较,哪种方法精度较高?你用什么方法比较它们之间的精度?
clc;clear;
f=@(x,y)2*y+x+2;
figure(1)
[x,y]=ode23t(f,[1,2],1);
plot(x,y,'r');
[x,yy]=ode45(f,[1,2],1);
hold on
plot(x,yy,'b');
legend('ode23t','ode45');
[x,yyy]=ode23(f,[1,2],1);
figure(2)
plot(x,yyy);
syms y(x)
h=diff(y)==2*y+x+2;
hh=dsolve(h,y(0)==1);
hold on
ezplot(hh,[0,1]);
legend('数值解ode23','解析解');
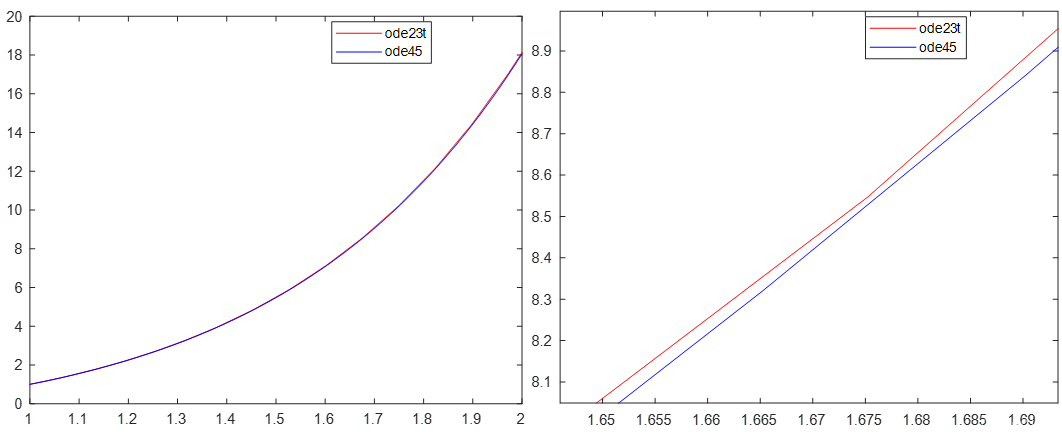
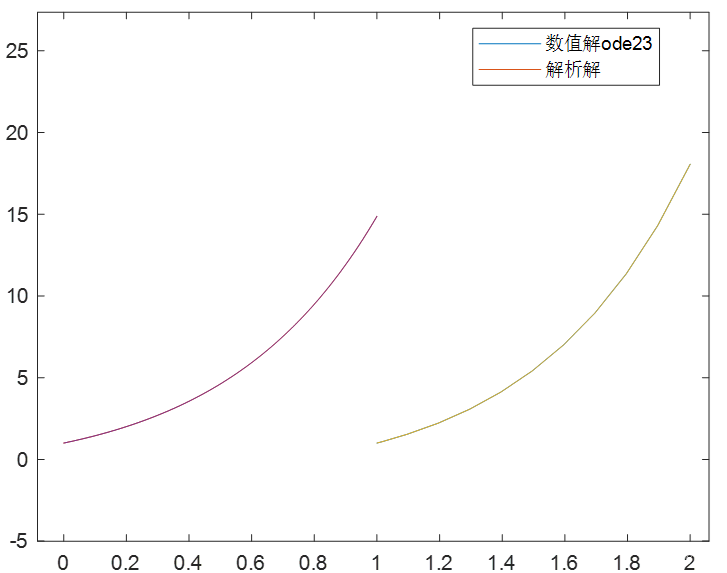
由上图我们可以发现,ode23所得到的数值解和解析解相差还是比较大的,而ode23t和ode45得到的数值解相差较小。
2.分别用命令ode23,ode23t和ode45求贝塞尔方程的数值解,并作出数值解曲线.
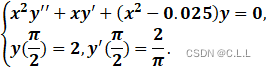
我们首先要将此微分方程改写为一阶方程(因为ode类函数只能解一阶可分离函数):
令y'=z ,则原方程化为:
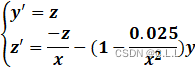
初值条件为:
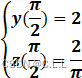
clc;clear;
f=@(x,m)[m(2);-m(2)/x-(1-(0.025/x^2)*m(1))];
[x,y]=ode23(f,[pi/2,2*pi],[2,2/pi]);
[xx,yy]=ode23t(f,[pi/2,2*pi],[2,2/pi]);
[xxx,yyy]=ode45(f,[pi/2,2*pi],[2,2/pi]);
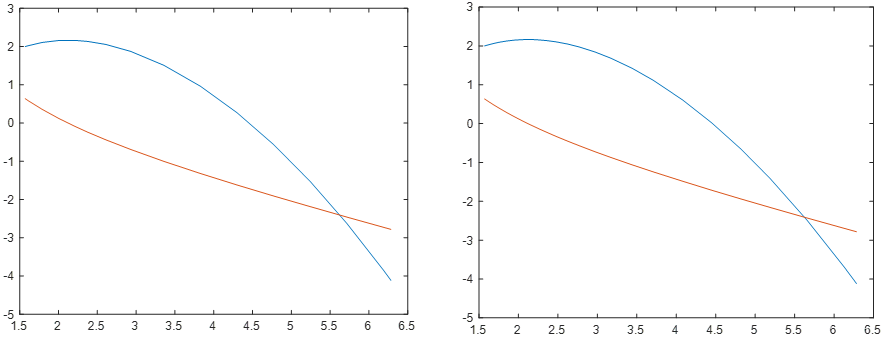
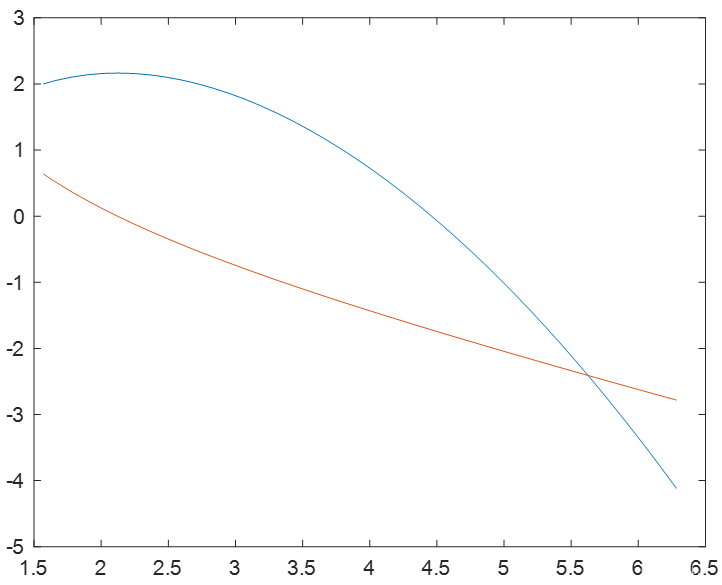
figure(1)
plot(x,y);
figure(2)
plot(xx,yy);
figure(3)
plot(xxx,yyy);
| x = 1.5708 1.6076 1.7914 2.0028 2.2100 2.3759 2.6091 2.9289 3.3577 3.8289 4.3001 4.7714 5.2426 5.7139 6.1851 6.2832 | y = 2.0000 0.6366 2.0225 0.5864 2.1086 0.3549 2.1583 0.1202 2.1615 -0.0861 2.1345 -0.2387 2.0552 -0.4382 1.8743 -0.6907 1.5104 -1.0022 0.9625 -1.3201 0.2691 -1.6204 -0.5627 -1.9084 -1.5280 -2.1874 -2.6232 -2.4596 -3.8453 -2.7265 -4.1155 -2.7815 | xx = 1.5708 1.5944 1.6415 1.6887 1.7479 1.8522 1.9564 2.0607 2.1280 2.1953 2.2626 2.3602 2.4785 2.6247 2.7709 2.9705 3.1701 3.4413 3.7126 4.0812 4.4497 4.8183 5.1869 5.6581 6.1294 6.2832 | yy = 2.0000 0.6366 2.0143 0.6046 2.0413 0.5416 2.0654 0.4809 2.0917 0.4073 2.1278 0.2846 2.1514 0.1694 2.1634 0.0605 2.1652 -0.0069 2.1625 -0.0722 2.1556 -0.1356 2.1380 -0.2247 2.1052 -0.3284 2.0483 -0.4512 1.9737 -0.5688 1.8448 -0.7225 1.6859 -0.8695 1.4242 -1.0608 1.1116 -1.2441 0.6089 -1.4833 0.0198 -1.7138 -0.6531 -1.9374 -1.4074 -2.1556 -2.4875 -2.4285 -3.6949 -2.6960 -4.1163 -2.7823 | xxx = 1.5708 1.5939 1.6170 1.6401 1.6632 1.7786 1.8941 2.0095 2.1250 2.2428 2.3606 2.4784 2.5962 2.7140 2.8319 2.9497 3.0675 3.1853 3.3031 3.4209 3.5387 3.6565 3.7743 3.8921 4.0100 4.1278 4.2456 4.3634 4.4812 4.5990 4.7168 4.8346 4.9524 5.0702 5.1880 5.3059 5.4237 5.5415 5.6593 5.7771 5.8949 5.9920 6.0890 6.1861 6.2832 | yyy = 2.0000 0.6366 2.0143 0.6049 2.0279 0.5738 2.0408 0.5432 2.0530 0.5132 2.1039 0.3701 2.1389 0.2374 2.1591 0.1132 2.1653 -0.0038 2.1581 -0.1171 2.1379 -0.2249 2.1053 -0.3282 2.0608 -0.4275 2.0047 -0.5234 1.9376 -0.6162 1.8596 -0.7064 1.7712 -0.7942 1.6726 -0.8800 1.5640 -0.9639 1.4455 -1.0461 1.3175 -1.1268 1.1801 -1.2061 1.0334 -1.2842 0.8776 -1.3612 0.7127 -1.4371 0.5390 -1.5121 0.3565 -1.5862 0.1653 -1.6596 -0.0345 -1.7322 -0.2428 -1.8042 -0.4596 -1.8755 -0.6847 -1.9462 -0.9181 -2.0164 -1.1598 -2.0861 -1.4097 -2.1554 -1.6676 -2.2242 -1.9337 -2.2926 -2.2078 -2.3606 -2.4899 -2.4283 -2.7799 -2.4956 -3.0779 -2.5626 -3.3293 -2.6176 -3.5861 -2.6724 -3.8481 -2.7270 -4.1155 -2.7814 |
此题要学会微分方程组该如何去解决。
3.17世纪末至18世纪初,牛顿发现在较小的温度范围内,物体冷却速率正比于该物体与环境温度的差值,因而得冷却模型
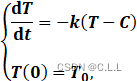
式中T(t)为物体t时刻的温度,C是环境温度,为正的常数,T0![]() 为物体在=0时刻的温度,其解为
为物体在=0时刻的温度,其解为
![]()
根据该冷却模型,完成下面的实验任务:
(1)某天晚上23:00时,在一住宅内发现一受害者的尸体,法医于23:35 赶到现场,立即测量死者体温是30.8℃,一小时后再次测量体温为29.1℃,法医还注意到当时室温是28℃,试估计受害者的死亡时间.
clc;clear;
format long
syms k m
f=@(t)9*exp(-k*t)+28;
f(m+35),f(m+95)
% 9*exp(-k*(m + 35)) + 28
% 9*exp(-k*(m + 95)) + 28
fsolve('fun',[1,5])
function f=fun(x)
f(1)=9*exp(-x(1)*(x(2) + 35)) + 28;
f(2)=9*exp(-x(1)*(x(2) + 95)) + 28;
end
ans =
4 3
由此可知,尸体的死亡时间为11:57.
(2)一个煮熟的鸡蛋在温度为98 ℃时放人温度为18℃的水中,5 min后鸡蛋的温度是 38℃,假设水的温度几乎没有升高,需要多长时间鸡蛋的温度可以达到20℃?
clc;clear;
format long
syms k m t
f=@(t)(98-18)*exp(-k*t)+18;
k=double(solve(f(5)==38));
k0=0.277258872223978;
f=@(t)(98-18)*exp(-k0*t)+18;
double(solve(f(t)==20))
ans =13.304820237218411;
4.承接此次实验中练习1的第2题,如图12.7所示.图中,两个容器完全相同,容器1排水孔的半径为0.02m,容器2排水孔的半径为0.01m,假如容器1装满水,容器2内水面的高度是1m,同时开启排水孔,完成下面的实验任务:
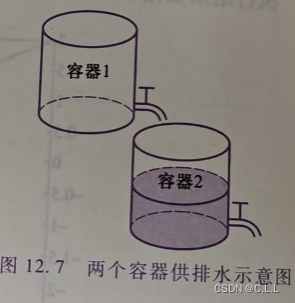
(1)经多长时间两个容器水面高度相同?
(2)求出容器2水面的高度与时间的函数关系,并求经多长时间容器2可以排空?
(3)在同一坐标系上画出两个容器内水面高度与时间的函数曲线进行比较.
(4)自己设定排水孔的半径与各容器的初始水位,将该容器排供水问题推广到n个容器的一般情况,建立一个简单的数学模型并求相关解.
我们假设水桶底面半径为1m,桶高4m;
clc;clear;
format short
m=4;r=1;
syms h(t) k
m1=-r^2*pi*diff(h)==k*sqrt(h)*pi*0.02^2;
h1=dsolve(m1,h(0)==m);
k=4.43;
h1=eval(h1(2))
%h1=((443*t)/500000 - 2)^2;
m2=-r^2*diff(h)==0.02^2*k*(2-(443*t)/500000)-0.01^2*k*sqrt(h);
h2=dsolve(m2)
f=@(t)(t - 1000000/443)^2/((500*67823512885646425253349271511524613553^(1/2))/3620155077721425633 + 62500/443)^2;
此题未写完,感觉不是很清楚,还请高人指点。
推荐下一篇文章:
数学实验第三版(主编:李继成 赵小艳)课后练习答案(十二)(4)![]() https://blog.csdn.net/2301_80199493/article/details/136136025?spm=1001.2014.3001.5501本文由作者自创,由于时间原因,难免出现些许错误,还请大家多多指正。创作不易,请大家多多支持。
https://blog.csdn.net/2301_80199493/article/details/136136025?spm=1001.2014.3001.5501本文由作者自创,由于时间原因,难免出现些许错误,还请大家多多指正。创作不易,请大家多多支持。
相关文章:
数学实验第三版(主编:李继成 赵小艳)课后练习答案(十二)(3)
实验十二:微分方程模型 练习三 1.分别用数值解命令ode23t和ode45 计算示例3中微分方程的数值解,同用命令ode23 算得的数值解以及解析解比较,哪种方法精度较高?你用什么方法比较它们之间的精度? clc;clear; f(x,y)2*yx2; figure(1) [x,y]ode23t(f,[1,2],1); plo…...

CSS Transition:为网页元素增添优雅过渡效果
随着互联网的发展,网页的视觉效果和用户体验变得尤为重要。CSS Transition作为一种能够让网页元素在状态改变时呈现平滑过渡效果的工具,受到了广大前端开发者的青睐。本文将详细介绍CSS Transition的基本概念、使用方法以及常见应用,帮助读者…...
)
JDK 17 新特性 (一)
既然 Springboot 3.0 强制使用 JDK 17 那就看看 JDK17 有哪些新特性吧 参考链接 介绍一下 新特性的历史渊源 JDK 17是Java Development Kit(JDK)的一个版本,它是Java编程语言的一种实现。JDK 17于2021年9月14日发布,并作为Java …...
杨中科 ASP.NET DI综合案例
综合案例1 需求说明 1、目的:演示DI的能力; 2、有配置服务、日志服务,然后再开发一个邮件发送器服务。可以通过配置服务来从文件、环境变量、数据库等地方读取配置,可以通过日志服务来将程序运行过程中的日志信息写入文件、控制台、数据库等。 3、说明…...

蓝桥杯嵌入式第12届真题(完成) STM32G431
蓝桥杯嵌入式第12届真题(完成) STM32G431 题目 程序 main.c /* USER CODE BEGIN Header */ /********************************************************************************* file : main.c* brief : Main program body**************************…...
)
C#系列-多线程(4)
在C#中,多线程编程主要涉及使用System.Threading命名空间下的类和接口来创建和管理线程。以下是一些C#多线程编程的基本用法和示例: 1. 使用Thread类创建线程 csharp代码 using System; using System.Threading; class Program { static void …...
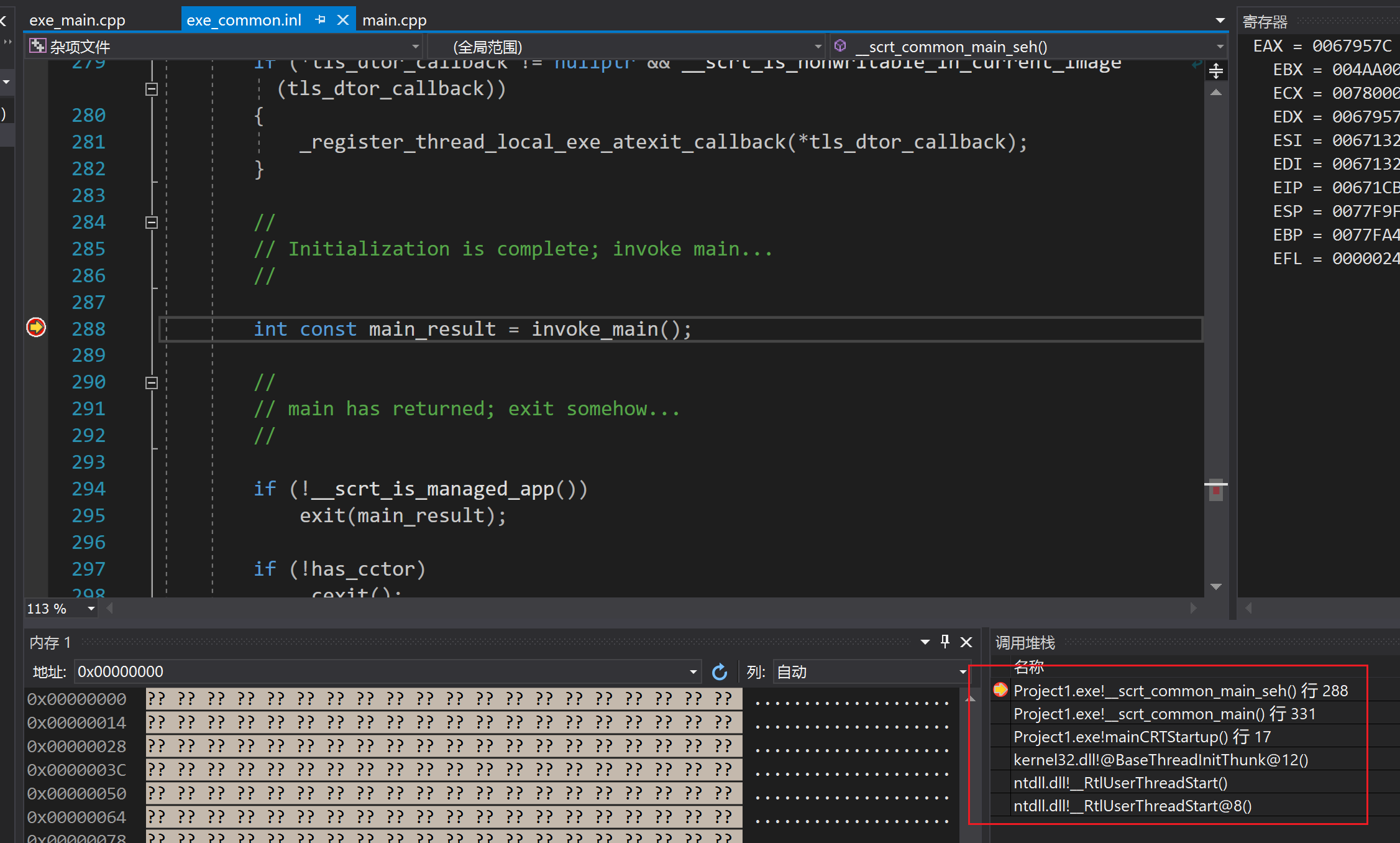
VS如何调试C运行时库
C运行时库(简称crt)是C标准库等组件的基础, 其会在进入main函数之前运行一些代码, 包括但不限于初始化堆栈, 内存分配等操作 这些代码是可以随着VC工具集一起安装到我们本地的。看一下这个情况, 就是VS调试器没找到对应的crt源码的情况, 调用堆栈是空的。为了解决这个问…...

软件工程师,超过35岁怎么办
概述 随着科技行业的飞速发展,软件开发工程师的职业道路充满了各种机遇和挑战。对于已经在这个行业摸爬滚打了十多年的软件开发工程师来说,当他们步入35岁这个年纪时,可能会感到一些迷茫和焦虑。许多人担忧,在以创新、活力、快速迭…...
)
通过 Prometheus 编写 TiDB 巡检脚本(脚本已开源,内附链接)
作者丨 caiyfc 来自神州数码钛合金战队 神州数码钛合金战队是一支致力于为企业提供分布式数据库 TiDB 整体解决方案的专业技术团队。团队成员拥有丰富的数据库从业背景,全部拥有 TiDB 高级资格证书,并活跃于 TiDB 开源社区,是官方认证合作伙…...

sql语句学习(一)--查询
【有道云笔记】基本sql语句2—查询基础 数据库表结构 DROP TABLE IF EXISTS class; CREATE TABLE class (id int(11) NOT NULL AUTO_INCREMENT,class_num varchar(11) CHARACTER SET utf8mb4 COLLATE utf8mb4_bin NOT NULL COMMENT 班级号,class_name varchar(255) CHARACTE…...

【HTML】交友软件上照片的遮罩是如何做的
笑谈 我不知道大家有没有在夜深人静的时候感受到孤苦难耐,🐶。于是就去下了一些交友软件来排遣寂寞。可惜的是,有些交友软件真不够意思,连一些漂亮小姐姐的图片都要进行遮罩,完全不考虑兄弟们的感受,😠。所…...
【Java EE初阶十二】网络编程TCP/IP协议(一)
1. 网络编程 通过网络,让两个主机之间能够进行通信->就这样的通信来完成一定的功能,进行网络编程的时候,需要操作系统给咱们提供一组API,通过这些API来完成编程;API可以认为是应用层和传输层之间交互的路径…...

element-ui解决上传文件时需要携带请求数据的问题
一、问题描述 在前端使用element-ui进行文件上传时,需要携带请求头信息,比如Token。 二、问题解决 1. 表单实现 action置空添加:http-request属性覆盖默认的上传行为,实现自定义上传文件。注意:src后的图片路径如果是个网络请求(外链)&…...

【AI视野·今日NLP 自然语言处理论文速览 第七十九期】Thu, 18 Jan 2024
AI视野今日CS.NLP 自然语言处理论文速览 Thu, 18 Jan 2024 Totally 35 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Deciphering Textual Authenticity: A Generalized Strategy through the Lens of Large Language Semantics …...

Docker容器运行
1、通过--name参数显示地为容器命名,例如:docker run --name “my_http_server” -d httpd 2、容器重命名可以使用docker rename。 3、两种进入容器的方法: 3.1、Docker attach 例如: 每间隔一秒打印”Hello World”。 Sudo docker run…...

【计算机网络】网络层之IP协议
文章目录 1.基本概念2.协议头格式3.网段划分4.特殊的IP地址5.IP地址的数量限制6.私有IP地址和公网IP地址7.路由 1.基本概念 IP地址是定位主机的,具有一个将数据报从A主机跨网络可靠的送到B主机的能力。 但是有能力就一定能做到吗,只能说有很大的概率。…...
2024/2/17 图论 最短路入门 dijkstra 1
目录 算法思路 Dijkstra求最短路 AcWing 849. Dijkstra求最短路 I - AcWing 850. Dijkstra求最短路 II - AcWing题库 最短路 最短路 - HDU 2544 - Virtual Judge (vjudge.net) 【模板】单源最短路径(弱化版) P3371 【模板】单源最短路径…...

交通管理|交通管理在线服务系统|基于Springboot的交通管理系统设计与实现(源码+数据库+文档)
交通管理在线服务系统目录 目录 基于Springboot的交通管理系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户信息管理 2、驾驶证业务管理 3、机动车业务管理 4、机动车业务类型管理 四、数据库设计 1、实体ER图 五、核心代码 六、论文参考 七、最新计…...

最适合初学者的Python入门详细攻略,一文讲清,赶紧收藏!
前言 目前python可以说是一门非常火爆的编程语言,应用范围也非常的广泛,工资也挺高,未来发展也极好。 Python究竟应该怎么学呢,我自己最初也是从零基础开始学习Python的,给大家分享Python的学习思路和方法。一味的买…...

幻兽帕鲁新手游戏攻略分享
在幻兽帕鲁中,提高实力是玩家不断追求的目标。以下是一些提高实力的攻略: 1、升级和进化:通过战斗和完成任务,玩家可以获得经验值,提升自己的等级。随着等级的提升,玩家可以获得技能点,用于提升…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...

aurora与pcie的数据高速传输
设备:zynq7100; 开发环境:window; vivado版本:2021.1; 引言 之前在前面两章已经介绍了aurora读写DDR,xdma读写ddr实验。这次我们做一个大工程,pc通过pcie传输给fpga,fpga再通过aur…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
)
python数据结构和算法(1)
数据结构和算法简介 数据结构:存储和组织数据的方式,决定了数据的存储方式和访问方式。 算法:解决问题的思维、步骤和方法。 程序 数据结构 算法 算法 算法的独立性 算法是独立存在的一种解决问题的方法和思想,对于算法而言&a…...

vue3+el-table 利用插槽自定义数据样式
<el-table-column label"匹配度" prop"baseMatchingLevel"><template #default"scope"><div :style"{ color: scope.row.baseMatchingLevel > 0.8 ? #00B578 : #FA5151 }">{{ scope.row.baseMatchingLevel }}&l…...
)
Java中Git基础操作详解(clone、commit、push、branch)
Git是Java开发者必备的版本控制工具,以下是核心操作的详细说明及示例: 一、Git基础概念 仓库(Repository):存储代码的目录,包含所有版本历史。提交(Commit)…...
