ABC340 A-F题解
文章目录
- A
- 题目
- AC Code:
- B
- 题目
- AC Code:
- C
- 题目
- AC Code:
- D
- 题目
- AC Code:
- E
- 题目
- 思路
- 做法
- 时间复杂度
- AC Code:
- F
- 题目
- 思路
- AC Code:
A
题目
模拟即可,会循环都能写。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int a, b, d;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> a >> b >> d;for (int i = a; i <= b; i += d) cout << i << ' ';return 0;
}
B
题目
这个也是根据题面模拟,存一下序列的长度即可。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int q, a[100100];
int n;int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> q;while (q --) {int op, x;cin >> op >> x;if (op == 1) {n++;a[n] = x;}else {cout << a[n - x + 1] << '\n';}}return 0;
}
C
题目
可以用递归加优化来完成此题。我们让 f ( x ) f(x) f(x) 表示要擦除 x x x 和擦除它产生的数的代价。然后得到:
f ( x ) = f ( x / 2 ) + f ( x − x / 2 ) + x f(x) = f(x/2) + f(x - x / 2) + x f(x)=f(x/2)+f(x−x/2)+x
然后为了避免重复计算,用 map 存储 f ( x ) f(x) f(x) 的值。如果这个答案没有被计算就计算这个答案,否则直接返回之前存储的答案。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
long long n;
map<long long, long long> m;
long long f(long long x) {if (x < 2) return 0;if (!m[x]) {if (x % 2) {long long tmp1 = f(x / 2), tmp2 = f(x - x / 2);m[x] = tmp1 + tmp2 + x;}else {long long tmp = f(x / 2);m[x] = tmp + tmp + x;}}return m[x];
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;cout << f(n);return 0;
}
D
题目
把游戏抽象化为一个图,每一个阶段就是一个点,那么连接 i i i 和 i + 1 i + 1 i+1 的边的权值就是 A i A_i Ai,连接 i i i 和 X i X_i Xi 的边的权值就是 B i B_i Bi,然后跑一遍最短路即可。如果没有负权边就不要用 SPFA,容易被卡。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
int n, a[200100], b[200100], x[200100];
struct edge{int u, v, w, nxt;
};
edge ed[400100];
int edcnt, head[200100];
void addedge(int u, int v, int w){edcnt++;ed[edcnt].u = u;ed[edcnt].v = v;ed[edcnt].w = w;ed[edcnt].nxt = head[u];head[u] = edcnt;
}
long long dis[200100];
struct node {int x;long long dis;node(int x_, long long dis_) {x = x_;dis = dis_;}
};
bool operator <(node a, node b) {return a.dis > b.dis;
}
bool vis[514114];
void dijkstra() {priority_queue<node> pq;pq.push(node(1, 0));while (!pq.empty()) {int now = pq.top().x;pq.pop();if (vis[now]) {continue;}if (now == n) break;vis[now] = 1;for (int j = head[now]; j; j = ed[j].nxt) {int v = ed[j].v;if (dis[v] > dis[now] + ed[j].w) {dis[v] = dis[now] + ed[j].w;pq.push(node(v, dis[v]));}}}
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n;for (int i = 1; i < n; i ++) {cin >> a[i] >> b[i] >> x[i];addedge(i, i + 1, a[i]);addedge(i, x[i], b[i]);}memset(dis, 0x3f, sizeof(dis));dis[1] = 0;dijkstra();cout << dis[n];return 0;
}
E
题目
思路
我们发现,如果序列头尾相连,那么我们每次要放的都是一个连续的区间,可以看题目的 GIF 图自行理解。那么这个题就是区间修改,单点查询,一个典型的线段树或树状数组维护差分数组,我用的线段树。
做法
首先,如果我们的球数大于等于 n n n,那么就可以先放 k n kn kn 个球,将每一个盒子都放 k k k 个,对于剩下不足 n n n 个球,设有 p p p 个球,如果往后 p p p 个盒子没有超过 n n n,就把后 p p p 个盒子每一个盒子放一个球,否则,一直放到第 n n n 个盒子,再从第一个盒子开始,放完剩下的球。
时间复杂度
O ( n log 2 ( n ) ) O(n\log_2(n)) O(nlog2(n)),合格。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
long long n, m, a[200100], b[200100];
struct node{long long l, r;long long sum;
};
node t[1600100];
long long maketree(long long l, long long r, long long p) {t[p].l = l;t[p].r = r;if (l < r) {t[p].sum = maketree(l, (l + r) / 2, p * 2);t[p].sum += maketree((l + r) / 2 + 1, r, p * 2 + 1);}else {if (l) t[p].sum = a[l] - a[l - 1];else t[p].sum = 0;}return t[p].sum;
}
void add(long long i, long long k, long long p) {if (t[p].l <= i && t[p].r >= i) t[p].sum += k;else return;add(i, k, p * 2);add(i, k, p * 2 + 1);
}
long long get(long long l, long long r, long long p) {if (l <= t[p].l && t[p].r <= r) return t[p].sum;if (l > t[p].r || t[p].l > r) return 0;return get(l, r, p * 2) + get(l, r, p * 2 + 1);
}
void add1(long long l, long long r, long long k) {add(l, k, 1);if (r + 1 <= n) add(r + 1, -k, 1);
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> n >> m;for (long long i = 1; i <= n; i++) cin >> a[i];for (long long i = 1; i <= m; i++) cin >> b[i];for (long long i = 1; i <= m; i++) b[i]++;maketree(1, n, 1);for (long long i = 1; i <= m; i ++) {long long tmp = get(1, b[i], 1);add1(b[i], b[i], -tmp);long long tmp1 = tmp / n;add1(1, n, tmp1);long long tmp2 = tmp % n;if (tmp2 > n - b[i]) {add1(b[i] + 1, n, 1);add1(1, tmp2 - (n - b[i]), 1);}else {add1(b[i] + 1, b[i] + tmp2, 1);}}for (long long i = 1; i <= n; i ++) {cout << get(1, i, 1) << ' ';}cout << '\n';return 0;
}
F
题目
如果你知道了以 ( 0 , 0 ) , ( A , B ) , ( C , D ) (0, 0), (A, B), (C, D) (0,0),(A,B),(C,D) 为顶点的三角形的面积为 ∣ A D − B C ∣ 2 \frac{|AD - BC|}{2} 2∣AD−BC∣,那么这个问题就很好解决了。
思路
题目给定了 X , Y X,Y X,Y,然后吧唧吧唧一大堆,就是想让我们求出一个 A , B A, B A,B,使得 ∣ A Y − B X ∣ 2 \frac{|AY-BX|}{2} 2∣AY−BX∣ 为 1 1 1,转换一下,就是 ∣ A Y + ( − B ) X ∣ = 1 |AY+(-B)X| = 1 ∣AY+(−B)X∣=1,这不就是典型的扩展欧几里得吗?
我们设 g g g 为 gcd ( X , Y ) \gcd(X, Y) gcd(X,Y),如果 g ≥ 3 g \ge 3 g≥3 那么说明无解,因为当 A X + B Y = gcd ( A , B ) AX + BY = \gcd(A,B) AX+BY=gcd(A,B) 时该方程才有解。将 − Y , X -Y, X −Y,X 带入上述方程求出 A , B A, B A,B,将 A , B A, B A,B 分别乘上 2 g \frac2g g2 就可以得到正确的答案。因为我们要求 A X + B Y = 2 AX + BY = 2 AX+BY=2,而现在是 A X + B Y = g AX +BY = g AX+BY=g,左右两边同时乘上 2 g \frac2g g2 即可。
AC Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <list>
#include <set>
#include <map>
using namespace std;
long long x, y;
long long e_gcd(long long a, long long b, long long &x, long long &y) {if (!b) {x = 1ll;y = 0ll;return a;}long long gcd = e_gcd(b, a % b, y, x);y -= a / b * x;return gcd;
}
long long a, b;
long long gcd(long long x, long long y) {if (y == 0ll) return x;return gcd(y, x % y);
}int main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin >> x >> y; long long g = gcd(x, y);e_gcd(y, -x, a, b);if (abs(g) >= 3ll) {cout << -1ll;return 0;}a *= 2ll / g, b *= 2ll / g;cout << a << ' ' << b;return 0;
}
相关文章:

ABC340 A-F题解
文章目录 A题目AC Code: B题目AC Code: C题目AC Code: D题目AC Code: E题目思路做法时间复杂度AC Code: F题目思路AC Code: A 题目 模拟即可,会循环都能写。 AC Code: #include …...

微软 CMU - Tag-LLM:将通用大语言模型改用于专业领域
文章目录 一、前言二、主要内容三、总结 🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 论文地址:https://arxiv.org/abs/2402.05140 Github 地址:https://github.com/sjunhongshen/Tag-LLM 大语言模型(…...

Kafka集群安装与部署
集群规划 准备工作 安装 安装包下载:链接:https://pan.baidu.com/s/1BtSiaf1ptLKdJiA36CyxJg?pwd6666 Kafka安装与配置 1、上传并解压安装包 tar -zxvf kafka_2.12-3.3.1.tgz -C /opt/moudle/2、修改解压后的文件名称 mv kafka_2.12-3.3.1/ kafka…...
C++初阶(十一) list
一、list的介绍及使用 1.1 list的介绍 list的文档介绍 1. list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 2. list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点…...
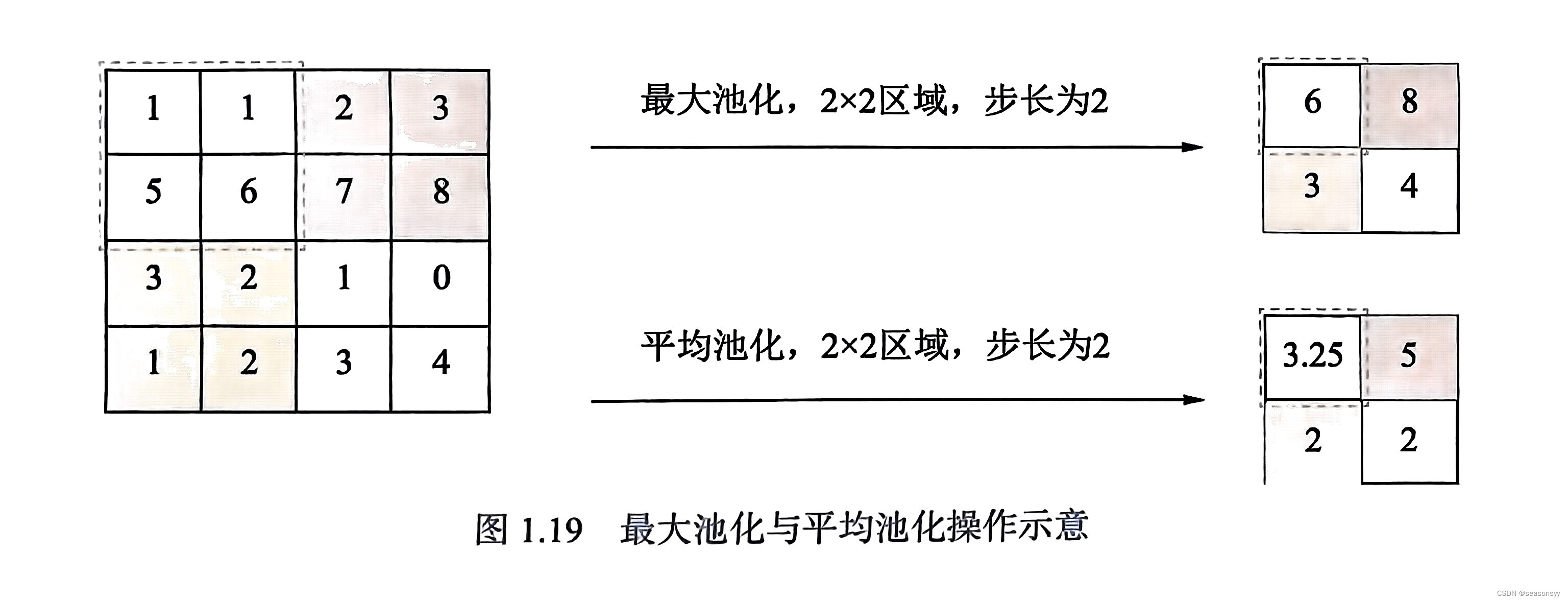
图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化
图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化 卷积神经网络的一些基本概念:图像卷积、步长、填充、特征图、多通道卷积、权重共享、感受野、池化 1.图像卷积、步长、填充 图像卷积:卷积核矩阵在一个原始图像矩阵上 “从上往下、…...
CMake进行C/C++与汇编混合编程
1. 前提 这篇文章记录一下怎么用CMake进行项目管理, 并用C/C和汇编进行混合编程, 为了使用这项技术, 必须在VS的环境中安装好cmake组件 由于大部分人不会使用C/C与汇编进行混合编程的情况。所以这篇文章并不适用于绝大部分人不会对其中具体细节进行过多叙述。只是做一些简单的…...

缓存预热!真香
预热一般指缓存预热,一般用在高并发系统中,为了提升系统在高并发情况下的稳定性的一种手段。 缓存预热是指在系统启动之前或系统达到高峰期之前,通过预先将常用数据加载到缓存中,以提高缓存命中率和系统性能的过程。缓存预热的目…...

VS中设置#define _CRT_SECURE_NO_WARNINGS的原因和设置方式
原因: 在编译老的用C语言的开源项目的时候,可能因为一些老的.c文件使用了strcpy,scanf等不安全的函数,而报警告和错误,而导致无法编译通过。 解决方案: 我们有两种解决方案: 1、在指定的源文件的开头定…...
【网站项目】155在线考试与学习交流网页平台
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...
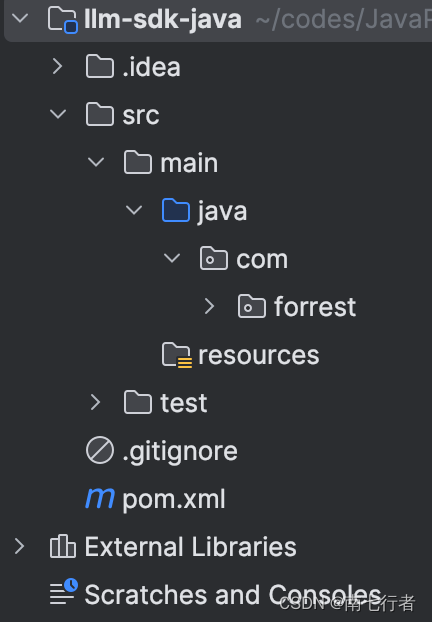
解决IDEA的Project无法正常显示的问题
一、问题描述 打开IDEA,结果发现项目结构显示有问题: 二、解决办法 File -> Project Structure… -> Project Settings (选Modules),然后导入Module 结果: 补充: IDEA提示“The imported module settings a…...

CDF和PDF的比较
以下内容来自ChatGPT,科技改变生活 Cumulative Distribution Function (CDF)(累积分布函数)和 Probability Density Function (PDF)(概率密度函数)是统计学和概率论中两个重要的概念,用于描述随机变量的性…...

编译基本过程 预处理器
编译基本过程 源代码(main.c)->预处理器(cpp)->编译器(gcc/clang/msvc)->汇编器(as)->链接器(ld)->可执行文件(main.exe) 预处理器 C语言中预处理器:执行预处理命令(文件包含、宏替换、条件编译)处理注释(将所有注释替换为空格)处理续行符(将所有…...

模拟算法.
1.什么是模拟 在信息奥赛中,有一类问题是模拟一个游戏的对弈过程或者模拟一项任务的操作过程.比如乒乓球在比赛中模拟统计记分最终判断输赢的过程等等,这些问题通常很难通过建立数学模型用特定的算法来解决因为它没有一种固定的解法,需要深刻理解出题者对过程的解释一般只能采…...

ClickHouse--10--临时表、视图、向表中导入导出数据
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.临时表1.1 特征1.2 创建一个临时表 2.视图2.1 普通视图2.2 物化视图 3.向表中导入导出数据3.1 案例 1.临时表 1.1 特征 ClickHouse 支持临时表,临时表…...

Python一些可能用的到的函数系列124 GlobalFunc
说明 GlobalFunc是算网的下一代核心数据处理基础。 算网是一个分布式网络,为了能够实现真的分布式计算(加快大规模任务执行效率),以及能够在很长的时间内维护不同版本的计算方法,需要这样一个对象/服务来支撑。Globa…...

python中线程/线程池,进程/进程池的创建
创建子线程 # 创建子线程t1 threading.Thread(targetjob,args(1,))# 执行子线程t1.start()# 等待子线程执行print("waiting threading")t1.join()print("threading done")创建子进程 # 创建子进程p1 multiprocessing.Process(targetjob,args(1,),name&qu…...

【c++】vector的增删查改
1.先定义一个类对象vector 为了防止和库里面发生冲突,定义一个命名空间,将类对象放在命名空间 里面 #include<iostream> using namespace std; namespace zjw {class vector {public:private:}; }2.定义变量,需要一个迭代器ÿ…...
【研究生复试】计算机软件工程人工智能研究生复试——资料整理(速记版)——JAVA
1、JAVA 2、计算机网络 3、计算机体系结构 4、数据库 5、计算机租场原理 6、软件工程 7、大数据 8、英文 自我介绍 1. Java 1. 和 equals的区别 比较基本数据类型是比较的值,引用数据类型是比较两个是不是同一个对象,也就是引用是否指向同 一个对象&…...

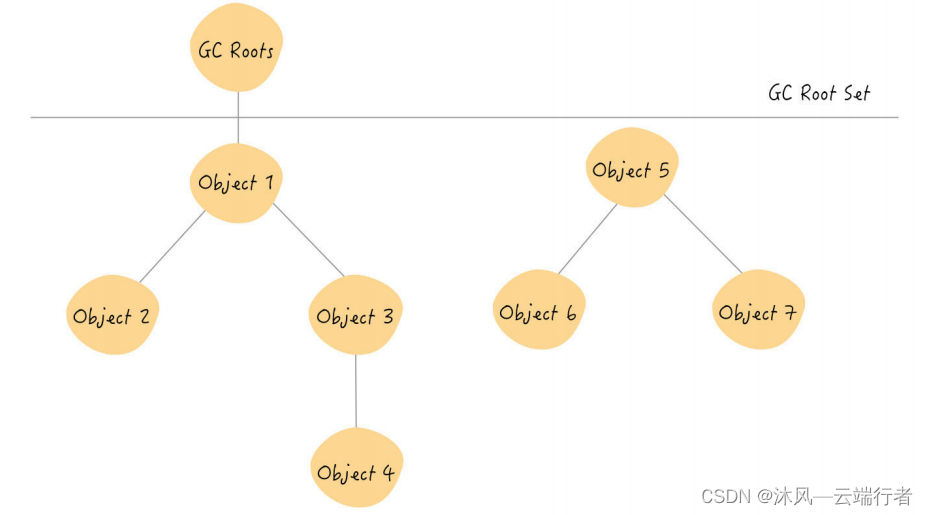
JVM-JVM中对象的生命周期
申明:文章内容是本人学习极客时间课程所写,文字和图片基本来源于课程资料,在某些地方会插入一点自己的理解,未用于商业用途,侵删。 原资料地址:课程资料 对象的创建 常量池检查:检查new指令是否能在常量池…...
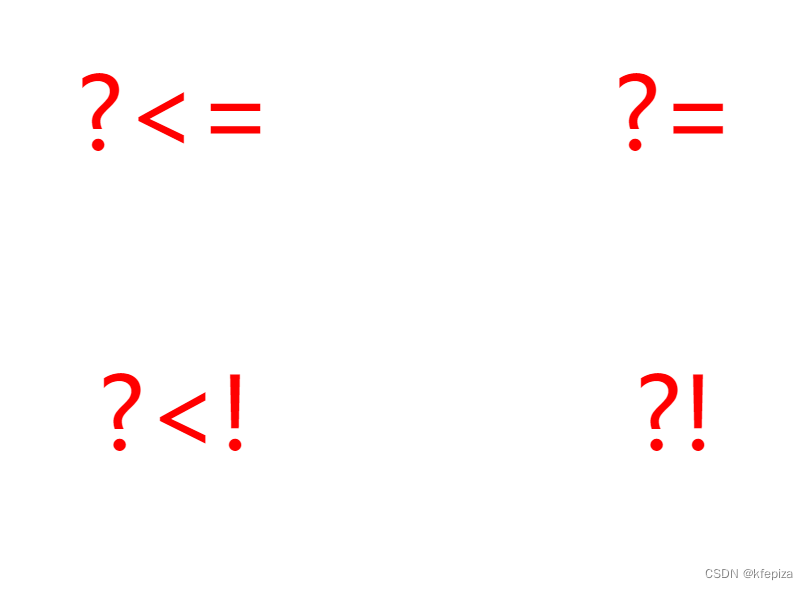
RegExp正则表达式左限定右限定左右限定,预查询,预查寻,断言 : (?<= , (?= , (?<! , (?!
RegExp正则表达式左限定右限定左右限定,预查询,预查寻,断言 : (?< , (? , (?<! , (?! 有好多种称呼 (?< , (? , (?<! , (?! 有好多种称呼 , 我称为: 左限定, 右限定, 左否定, 右否定 (?<左限定) (?右限定)(?<!左否定) (?!右限定) 再…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
