【详解】图的概念和存储结构(邻接矩阵,邻接表)
目录
图的基本概念:
图的存储结构
邻接矩阵(GraphByMatrix):
基本参数:
初始化:
获取顶点元素在其数组中的下标 :
添加边和权重:
获取顶点的度:
打印图:
邻接表(GraphByNode):
基本参数:
注意:
初始化:
获取顶点元素在其数组中的下标 :
添加边和权重:
获取顶点的度:
打印图:
结语:
图的基本概念:
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E)。
其中:
(1)顶点集合V = {x|x属于某个数据对象集}是有穷非空集合。
(2)E = {(x,y)|x,y属于V}或者E = {|x,y属于V && Path(x, y)}是顶点间关系的有穷集合,也叫做边的集合。
(3)(x, y)表示x到y的一条双向通路,即(x, y)是无方向的;Path表示从x到y的一条单向通路,即Path 是有方向的。
顶点和边:
图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边, 图中的第k条边记作ek,ek = (vi,vj)或。
有向图和无向图:
在有向图中,顶点对是有序的,顶点对称为顶点x到顶点y的一条边(弧),和是两条不同的边,比如下图G3和G4为有向图。在无向图中,顶点对(x, y)是无序的,顶点对(x,y) 称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)是同一条边,比如下图G1和G2为 无向图。注意:无向边(x, y)等于有向边和。
例如下图:G1和G2位无向图,G3和G4为有向图。
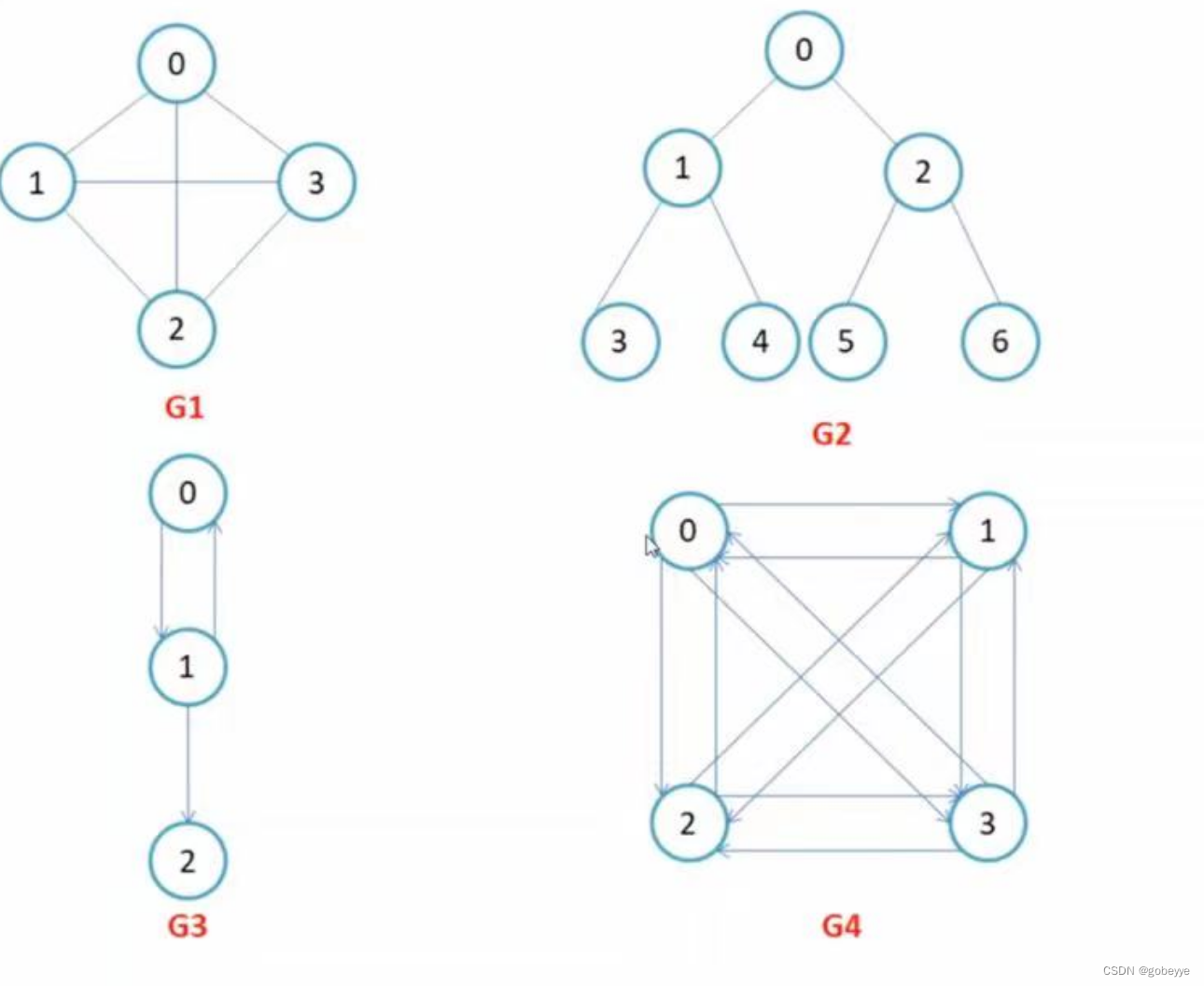
完全图:
在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边,则称此图为 无向完全图,比如上图G1;在n个顶点的有向图中,若有n * (n-1)条边,即任意两个顶点之间有且仅有方向 相反的边,则称此图为有向完全图,比如上图G4。
顶点的度:
顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与 出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向 边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注意:对于无向图,顶点的度等于该顶 点的入度和出度,即dev(v) = indev(v) = outdev(v)。
路径:
在图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
路径长度:
对于不带权的图,一条路径的路径长度是指该路径上的边的条数;对于带权的图,一条路径的路 径长度是指该路径上各个边权值的总和。
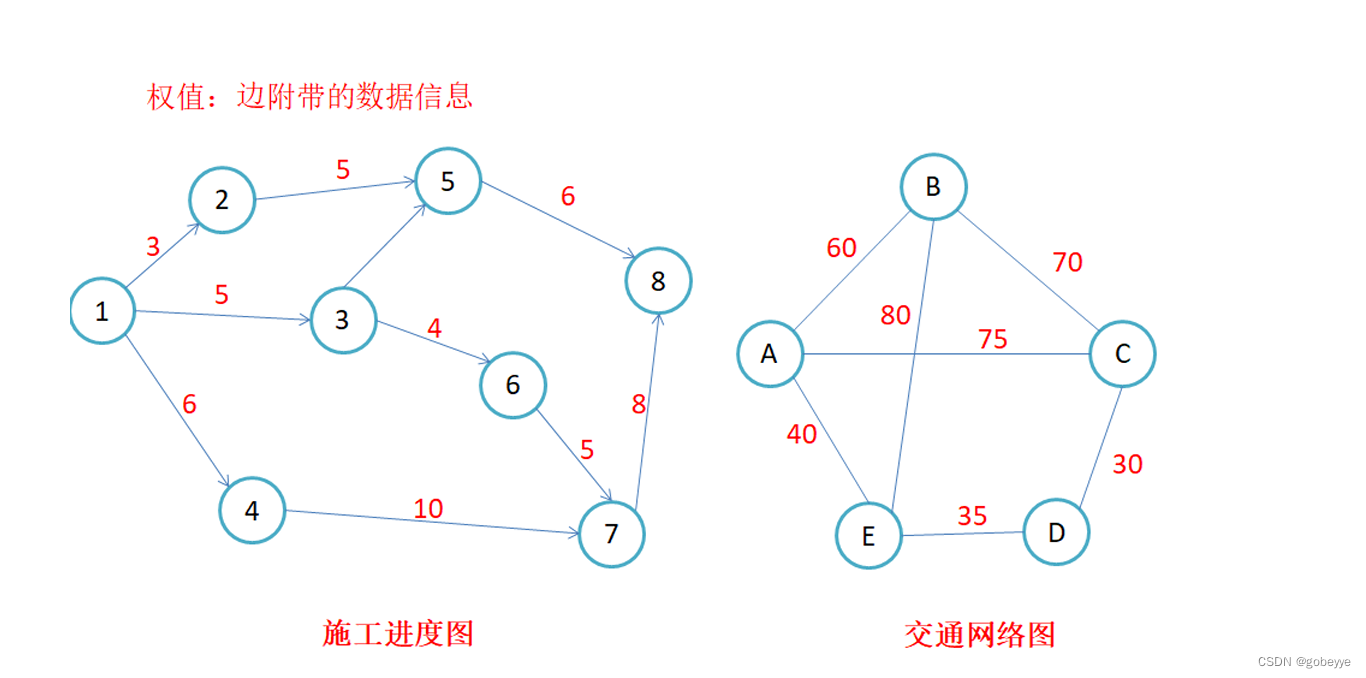
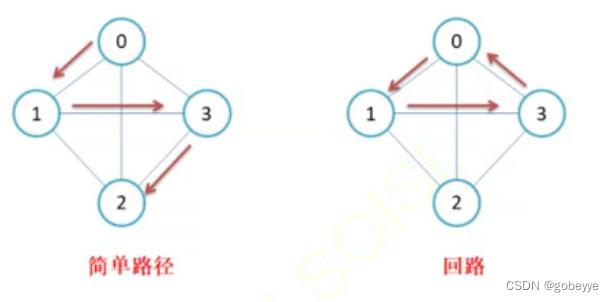
简单路径与回路:
若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路径。若路 径上 第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。例如下图:
子图:
设图G = {V, E}和图G1 = {V1,E1},若V1属于V且E1属于E,则称G1是G的子图。如下图:
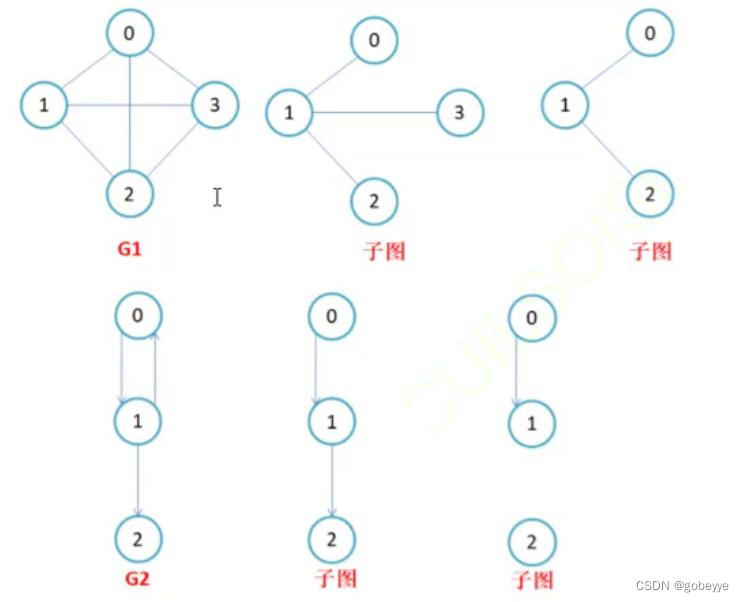
连通图:
在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一 对顶点 都是连通的,则称此图为连通图。
强连通图:
在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj到 vi的路 径,则称此图是强连通图。
生成树:
一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条 边。
图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。故图的存储结构有两种。1.邻接矩阵 2.邻接表。其中最常用的是邻接矩阵。
邻接矩阵(GraphByMatrix):
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定 点保存,然后采用矩阵来表示节点与节点之间的关系。
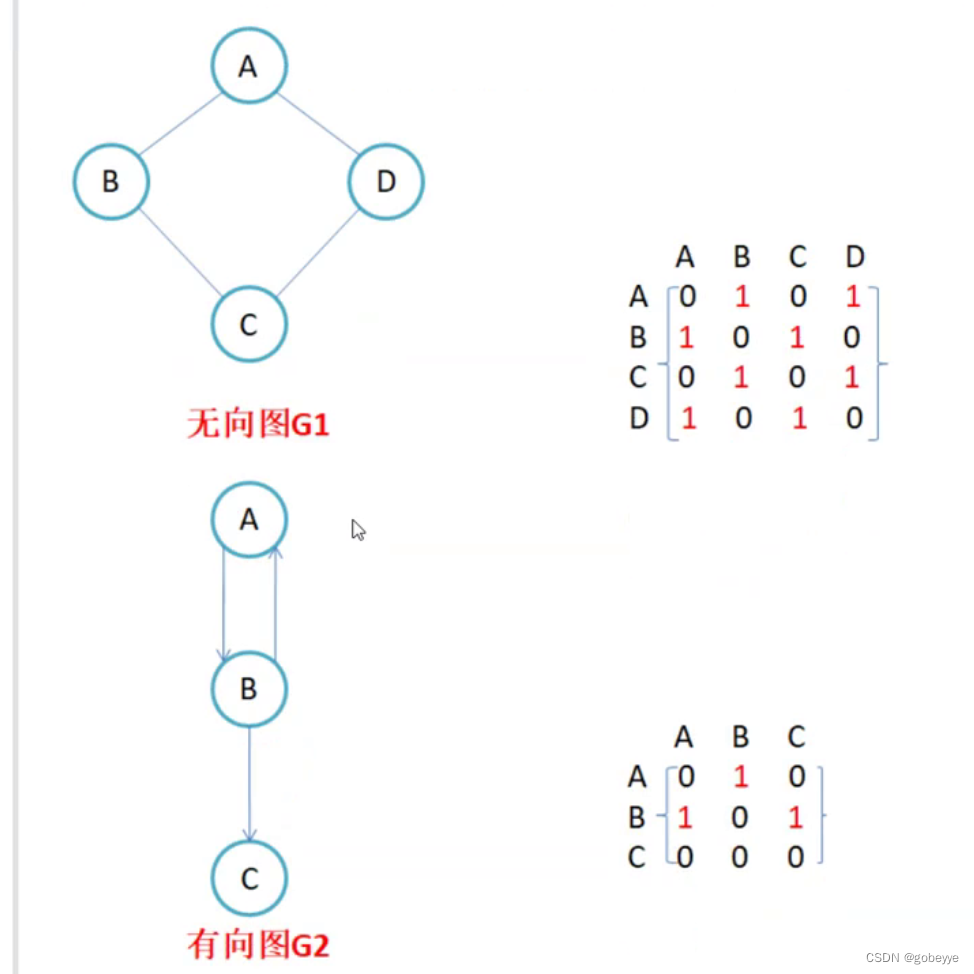
注意:
1. 无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。有向图的邻接矩阵则不一定是对称的,第i行(列)元素之后就是顶点i 的出(入)度。
2. 如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个顶点不通,则使用无穷大代替。
如下图:
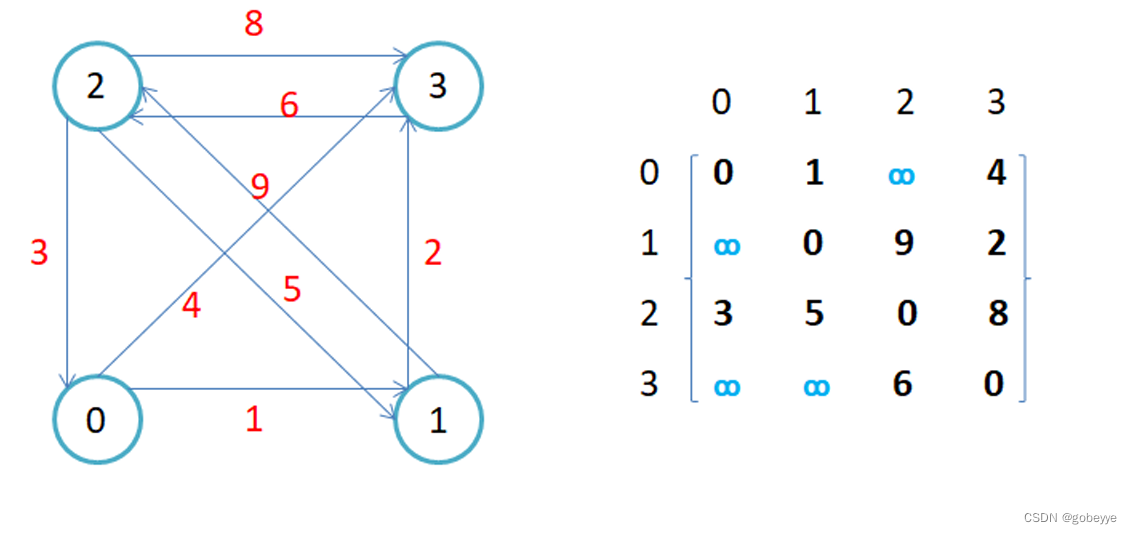
3. 用邻接矩阵存储图的优点是能够快速知道两个顶点是否连通,缺陷是如果顶点比较多,边比较少时,矩 阵中存储了大量的0成为系数矩阵,比较浪费空间,并且要求两个节点之间的路径不是很好求。
实现GraphByMatrix类,arrayv用来存放顶点,matrix来存放边,isDirect用来判断图是否是有向图。根据上面给出的注意2要用fill将数组初始化为无穷大。
基本参数:
public class GraphByMatrix {private char[] arrayV;//存放顶点·private int[][] matrix;//存放边private boolean isDirect;//是否是有向图public GraphByMatrix(int size,boolean isDirect){arrayV = new char[size];matrix = new int[size][size];for(int i = 0;i < size;i++){Arrays.fill(matrix[i],Integer.MAX_VALUE);}this.isDirect = isDirect;}
}初始化:
初始化arrayV顶点数组。
public void initArrayV(char[] array){for(int i = 0;i < array.length;i++){arrayV[i] = array[i];}}获取顶点元素在其数组中的下标 :
public int getIndexOfV(char v){for(int i = 0;i < arrayV.length;i++){if(v == arrayV[i]){return i;}}return -1;}添加边和权重:
先查找出两个顶点在,顶点数组中的位置,特别注意:无向图的话,两边都要设置,因为有向图每条边都是单独的。
public void addEdge(char v1,char v2,int weight){int index1 = getIndexOfV(v1);int index2 = getIndexOfV(v2);matrix[index1][index2] = weight;if(!isDirect){matrix[index2][index1] = weight;}}效果如下:
这是一个无向图,将边的关系抽象为二维数组,其中2^31-1为未赋予权重。
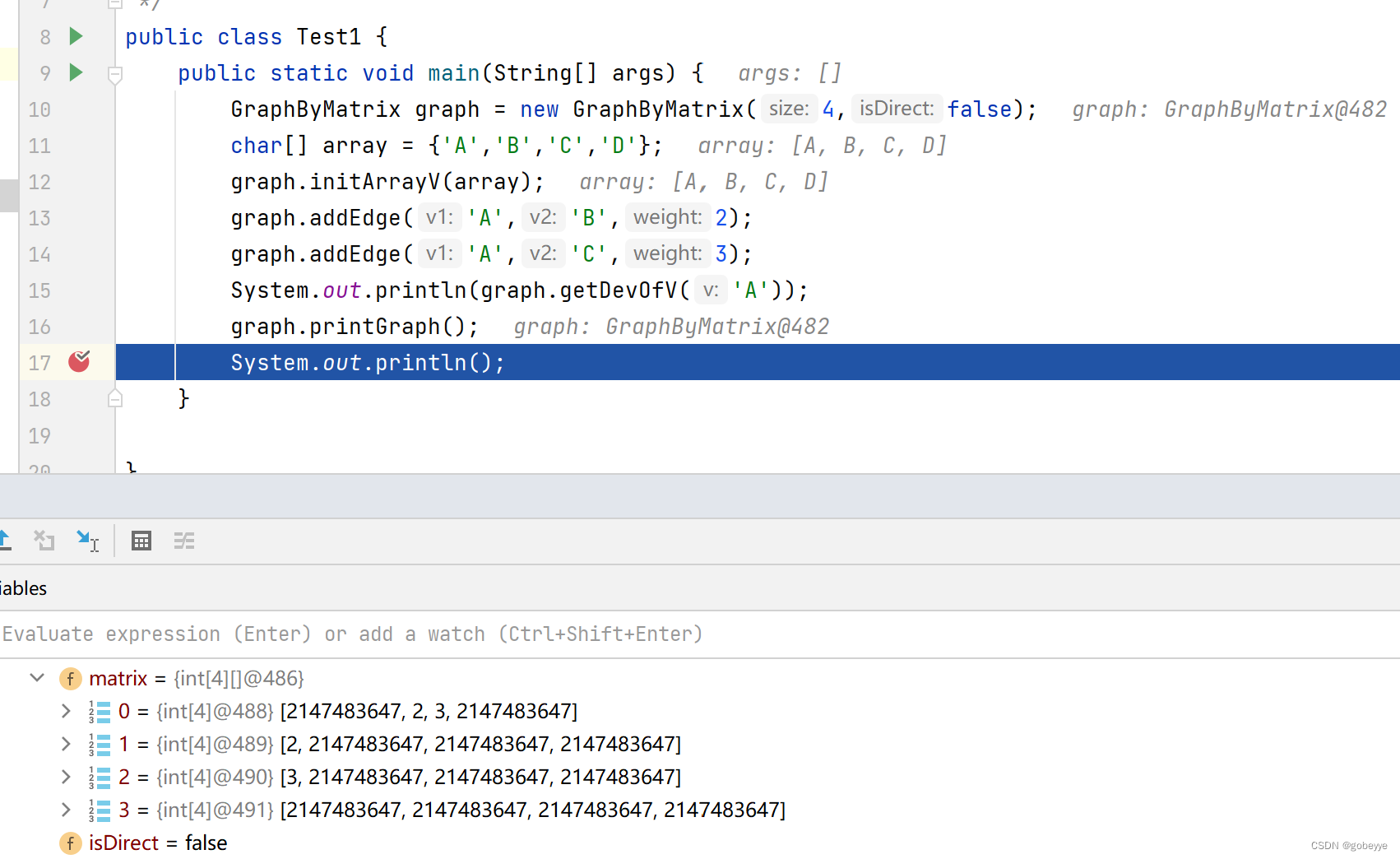
获取顶点的度:
1、现在顶点数组 arrayV 中找到顶点的下标。
2、无向图只需要计算出度就好了。
3、如果是有向图,有向图的度 = 入度 +出度。
4、此时的count中存储的就是顶点V的度。
第二个for循环是沿着y轴遍历。
public int getDevOfV(char v){int indexV = getIndexOfV(v);int count = 0;for(int i = 0;i < arrayV.length;i++){if(matrix[indexV][i] != Integer.MAX_VALUE){count++;}}if(isDirect){for(int i = 0;i < arrayV.length;i++){if(matrix[i][indexV] != Integer.MAX_VALUE){count++;}}}return count;}测试如下:
我们add了A的两条边故打印2.

打印图:
为了使打印效果更好我们将2^31-1打印为无穷大。
public void printGraph(){for(int i = 0;i < arrayV.length;i++){System.out.print(arrayV[i] + " ");}System.out.println();for(int i = 0;i < matrix.length;i++){for(int j = 0;j < matrix[i].length;j++){if(matrix[i][j] == Integer.MAX_VALUE) {System.out.print("∞ ");}else {System.out.print(matrix[i][j]+" ");}}System.out.println();}}效果如下:
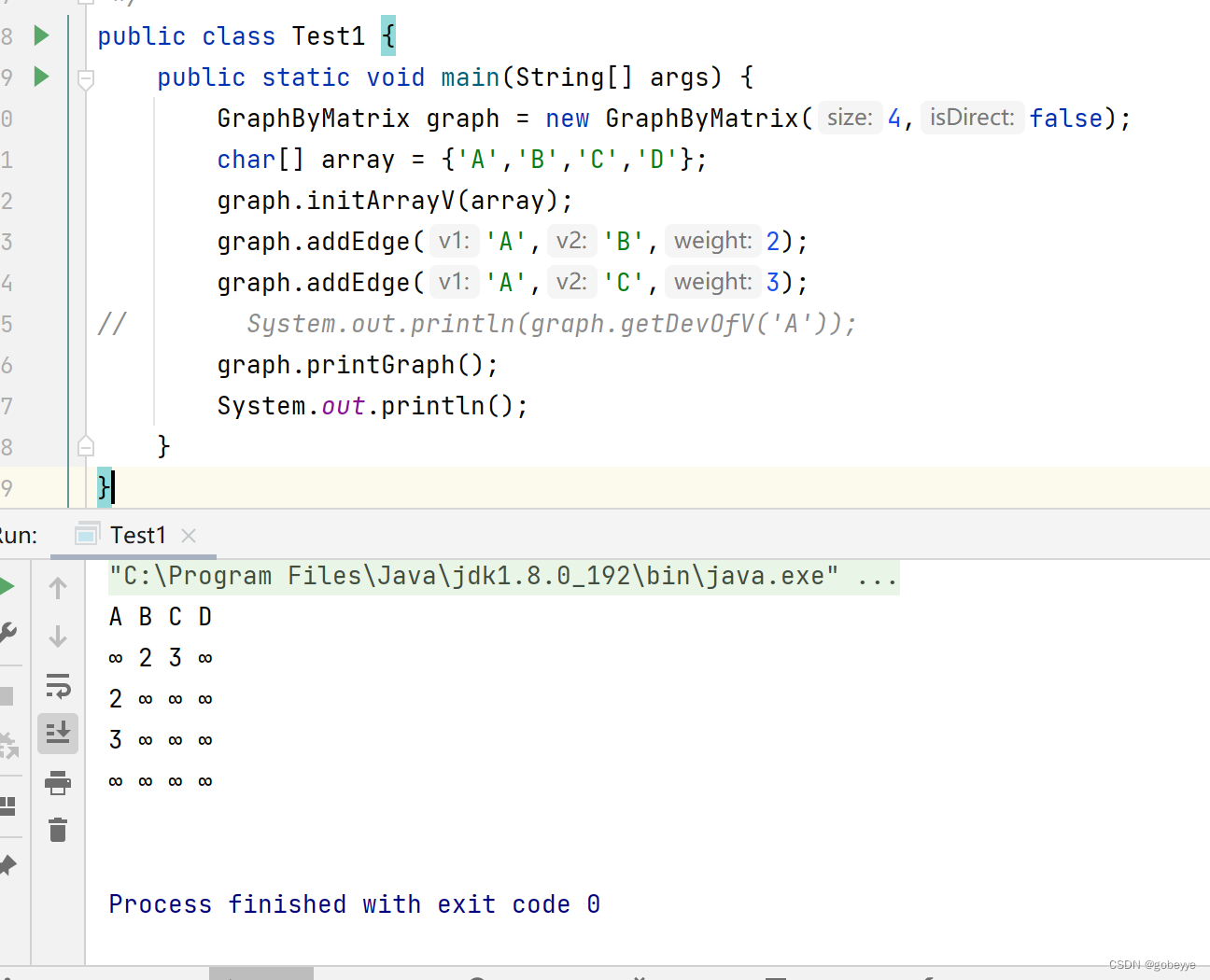
邻接表(GraphByNode):
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
1. 无向图邻接表存储

注意:无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度,只需要知道顶点vi边链表集 合中结点的数目即可。
2.有向图邻接表存储:
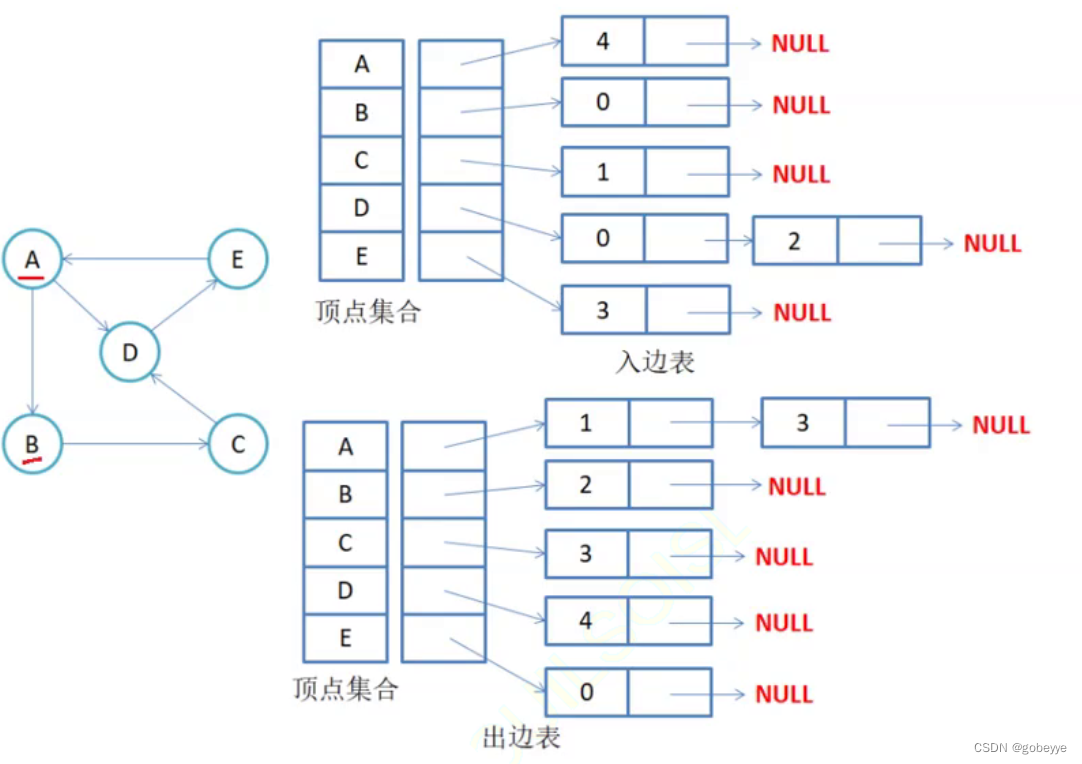
注意:有向图中每条边在邻接表中只出现一次,与顶点vi对应的邻接表所含结点的个数,就是该顶点的出度,也称出度表,要得到vi顶点的入度,必须检测其他所有顶点对应的边链表,看有多少边顶点的dst取值是i。
基本参数:
需要设置一个静态内部类Node结点,结点要能存储起始,终点,权重和下一结点的数据。运用数组加链表的存储方式。
public class GraphByNode {static class Node{public int src;//起始下标public int dest;//重点下标public int weight;//权重public Node next;public Node(int src,int dest,int weight){this.src = src;this.dest = dest;this.weight = weight;}}private ArrayList<Node> edgeList;private char[] arrayV;//存放顶点private boolean isDirect;//是否是有向图public GraphByNode(int size,boolean isDirect){arrayV = new char[size];edgeList = new ArrayList<>(size);for(int i = 0;i < size;i++){edgeList.add(null);}this.isDirect = isDirect;}
}注意:
new ArrayList<>(size)里面直接加参数是不能初始化list大小的例如:

我们可以看到size的大小为0这样在进行操作时就会报错。
解决方法如下:

这样就成功解决了💯。
初始化:
public void initArrayV(char[] array){for(int i = 0;i < array.length;i++){arrayV[i] = array[i];}}获取顶点元素在其数组中的下标 :
public int getIndexOfV(char v){for(int i = 0;i < arrayV.length;i++){if(arrayV[i] == v){return i;}}return -1;}添加边和权重:
为了使代码更加整洁在addEdge里面再调用addEdgeChild方法。注意区分有向图和无向图的区别,如果要添加的边已经再链表里了直接return退出添加失败而不是大多数的覆盖,用头插法插入数据。
public void addEdge(char v1,char v2,int weight){int src = getIndexOfV(v1);int dest = getIndexOfV(v2);addEdgeChild(src,dest,weight);if(!isDirect){addEdgeChild(dest,src,weight);}}private void addEdgeChild(int src,int dest,int weight){Node cur = edgeList.get(src);while(cur != null){if(cur.dest == dest){return;}cur = cur.next;}//头插法Node node = new Node(src,dest,weight);node.next = edgeList.get(src);edgeList.set(src,node);}效果如下:
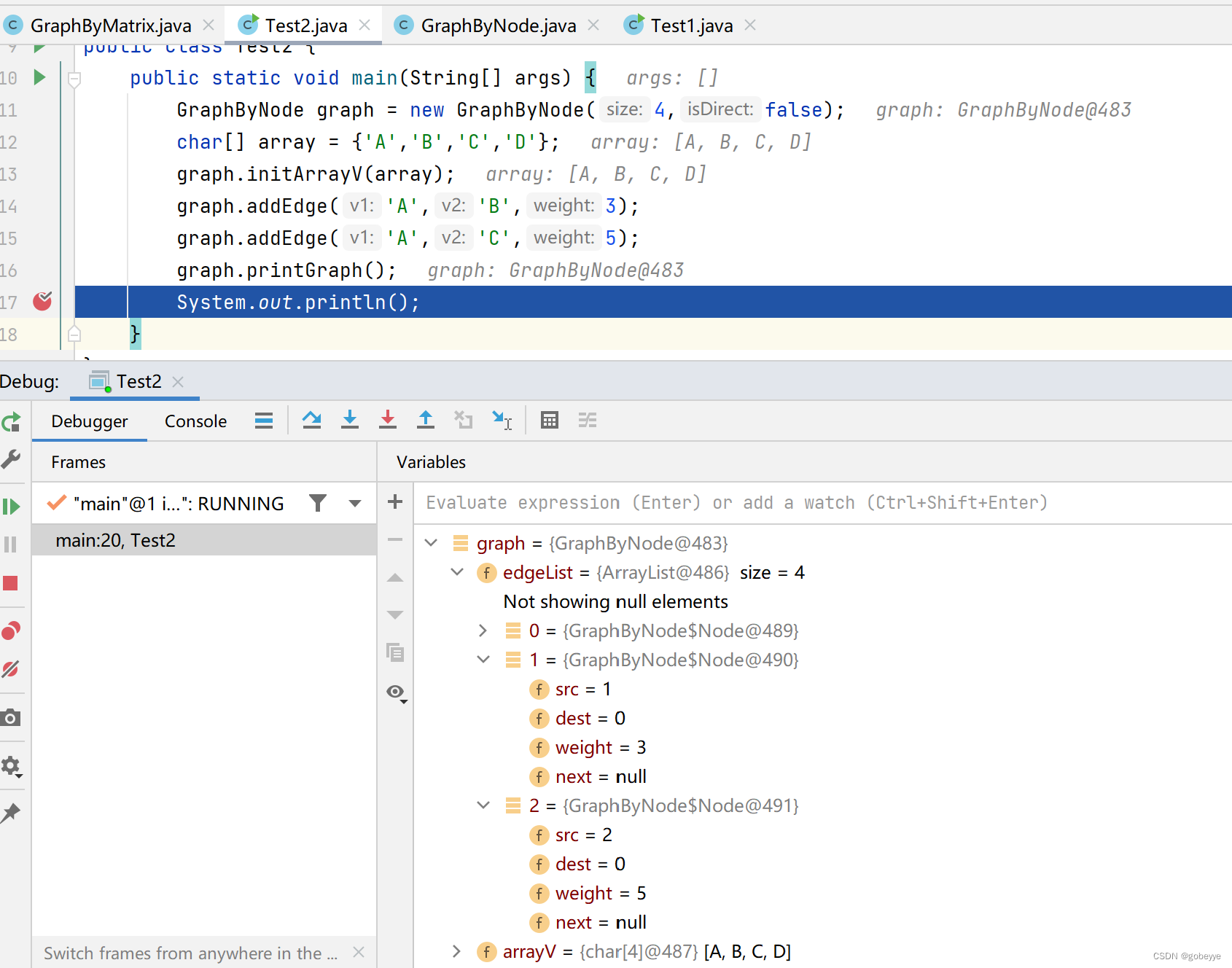
获取顶点的度:
1、现在顶点数组 arrayV 中找到顶点的下标。
2、如果是无向图,只需要遍历链表的节点个数。
3、如果是有向图,必须检测其他所有顶点对应的边链表,看有多少边顶点的dst取值是i //有向图也就一张表。
使用continue来跳过当前自己的顶点链表防止有重复。
public int getDevOfV(char v){int indexV = getIndexOfV(v);int count = 0;Node cur = edgeList.get(indexV);while(cur != null){count++;cur = cur.next;}if(isDirect){int dest = indexV;for(int src = 0;src < arrayV.length;src++){if(src == dest){continue;}else{Node pCur = edgeList.get(src);while(pCur != null){if(pCur.dest == dest){count++;}pCur = pCur.next;}}}}return count;}效果如下:
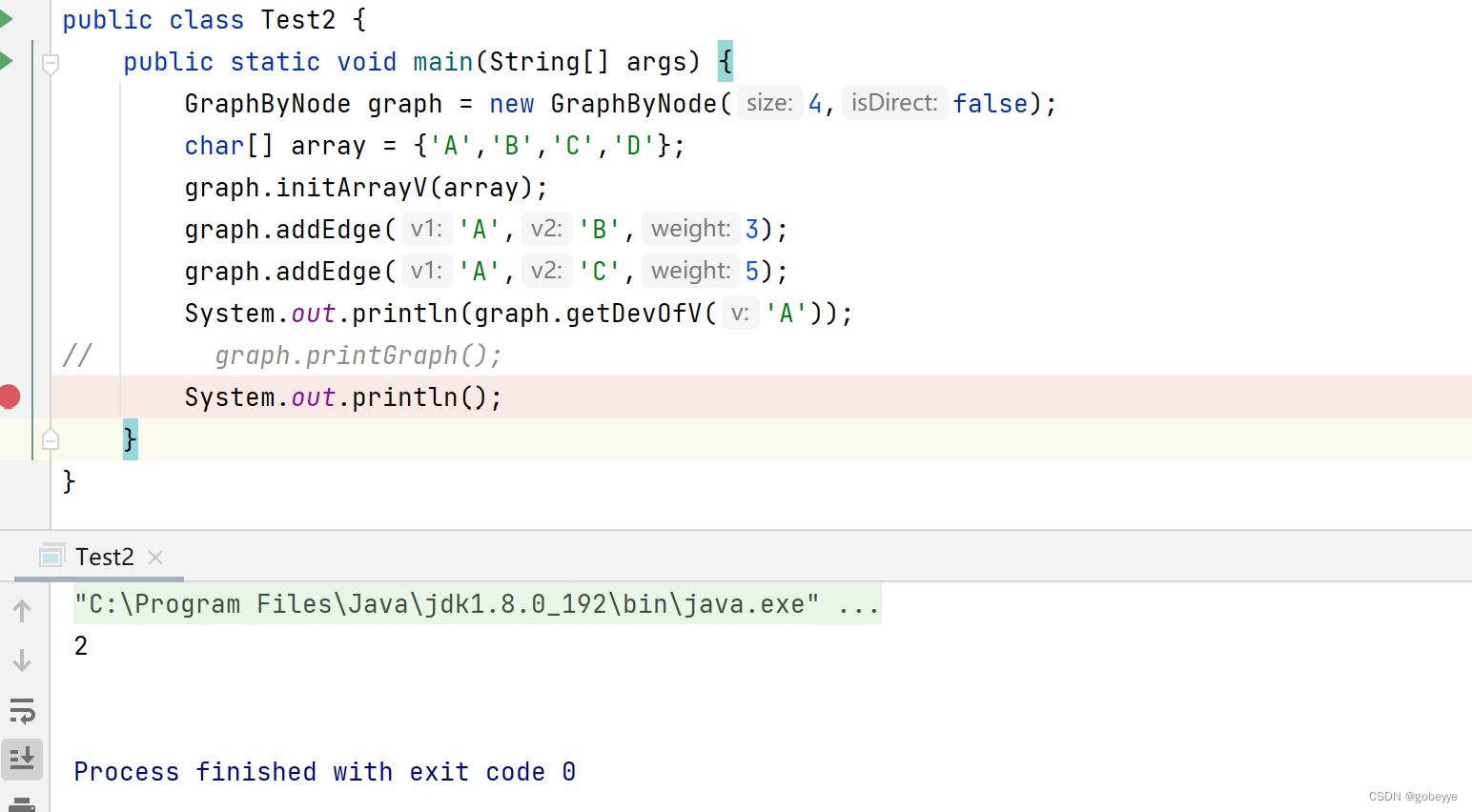
打印图:
public void printGraph(){for(int i = 0;i < arrayV.length;i++){System.out.print(arrayV[i] + "->");Node cur = edgeList.get(i);while(cur != null){System.out.print(cur.dest + "->");cur = cur.next;}System.out.println("null");}}效果如下:
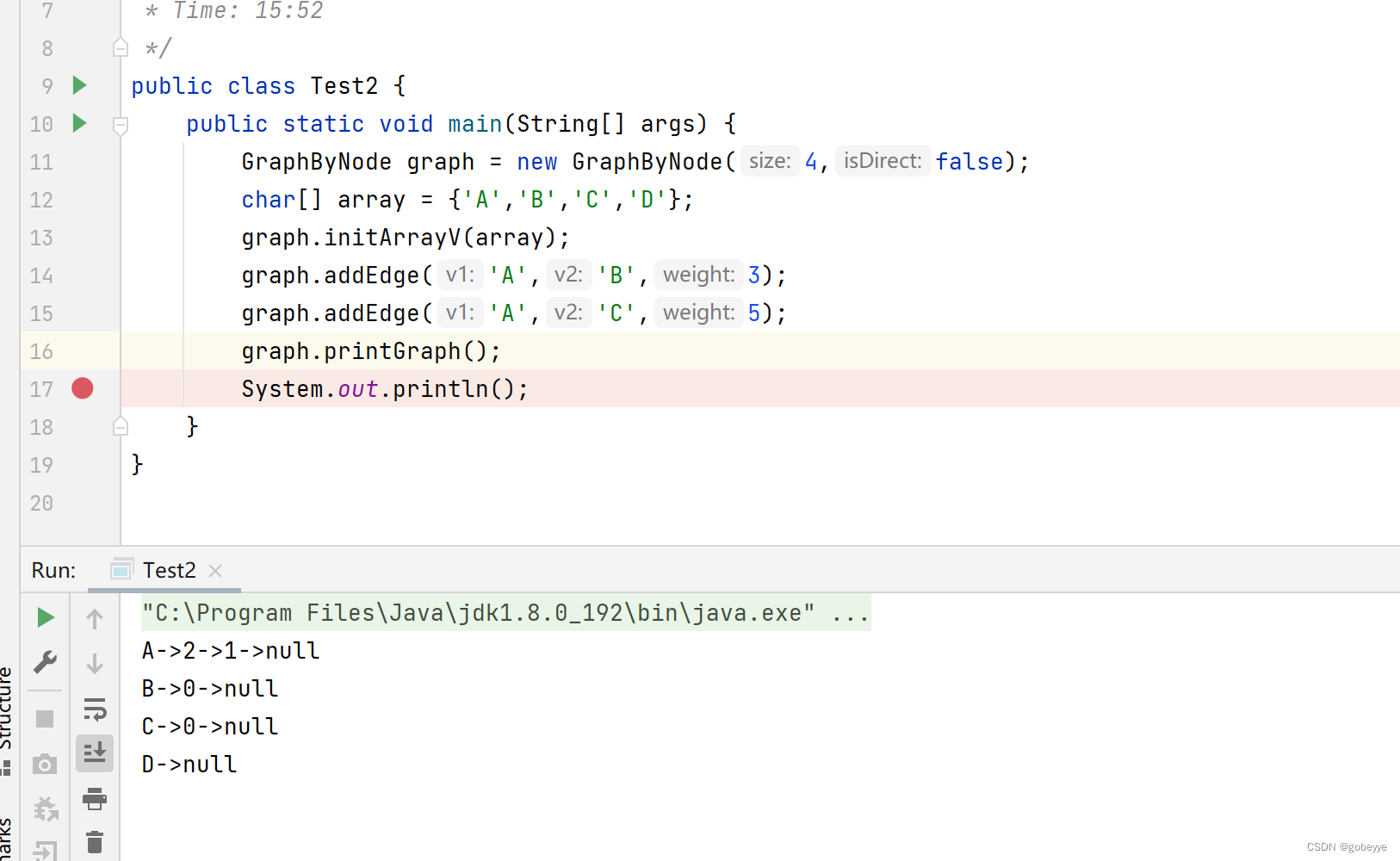
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固自己的知识点,和一个学习的总结,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进,如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。
相关文章:

【详解】图的概念和存储结构(邻接矩阵,邻接表)
目录 图的基本概念: 图的存储结构 邻接矩阵(GraphByMatrix): 基本参数: 初始化: 获取顶点元素在其数组中的下标 : 添加边和权重: 获取顶点的度: 打印图…...

【AIGC】Stable Diffusion介绍
Stable Diffusion 是一个基于 OpenAI 的 Diffusion 模型的扩展版本,它采用了稳定扩散(Stable Diffusion)的技术,旨在提高图像生成和处理的质量。下面是 Stable Diffusion 的详细介绍: 基于 Diffusion 的图像生成&…...
2024.2.18 C++QT 作业
思维导图 练习题 1>定义一个基类 Animal,其中有一个虛函数perform(),用于在子类中实现不同的表演行为。 #include <iostream>using namespace std;class Animal { public:virtual void perform() {cout << "这是一个动…...

【qt创建线程两种方式】
QT使用线程的两种方式 1.案例进度条 案例解析: 如图由组件一个进度条和三个按钮组成,当点击开始的时候进度条由0%到100%,点击暂停,进度条保持之前进度,再次点击暂停变为继续,点击停止按钮进度条停止。 案…...

网络安全-一句话木马
声明 遵纪守法 请严格遵守网络安全法相关条例! 此分享主要用于交流学习,请勿用于非法用途,一切后果自付。 一切未经授权的网络攻击均为违法行为,互联网非法外之地。 反制 大家在知道了常规一句话的木马之后,就可以通…...

在k8s中,使用DirectPV CSI作为分布式存储的优缺点
DirectPV 提供了一种直接将物理卷(Physical Volumes)与 Kubernetes 集群中的 Pod 绑定的机制。 利用 DirectPV,你可以将相应的 PV 直接与节点上的物理存储设备(如磁盘)进行绑定,而无需通过网络存储服务(如 NFS 或 Ceph)来提供存储。这种直接访问物理卷的方式,有助于提…...
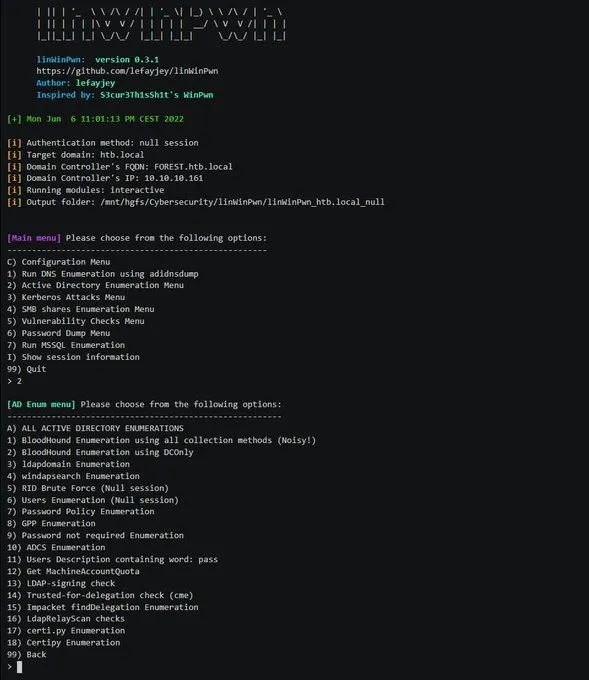
自动化AD域枚举和漏洞检测脚本
linWinPwn 是一个 bash 脚本,可自动执行许多 Active Directory 枚举和漏洞检查。该脚本基于很多现有工具实现其功能,其中包括:impacket、bloodhound、netexec、enum4linux-ng、ldapdomaindump、lsassy、smbmap、kerbrute、adidnsdump、certip…...
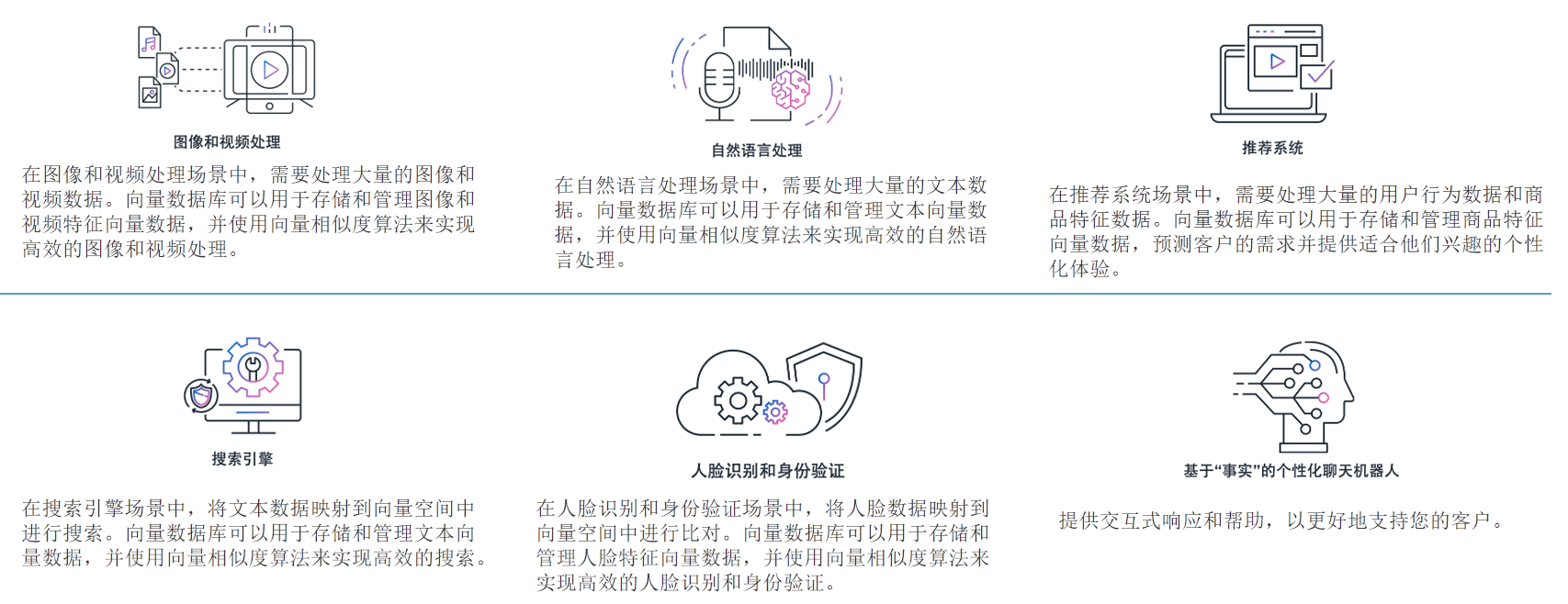
数据库管理-第151期 Oracle Vector DB AI-03(20240218)
数据库管理151期 2024-02-18 数据库管理-第151期 Oracle Vector DB & AI-03(20240218)1 向量数据库应用场景2 Oracle Vector DB3 Vector数据类型4 Vector运算5 Vector DML插入向量获取向量 总结 数据库管理-第151期 Oracle Vector DB & AI-03&am…...
Vue3+vite搭建基础架构(6)--- 使用vue-router
Vue3vite搭建基础架构(6)--- 使用vue-router 说明官方文档安装vue-router使用vue-router测试vue-router 说明 这里记录下自己在Vue3vite的项目使用vue-router的过程,不使用ts语法,方便以后直接使用。这里承接自己的博客Vue3vite搭…...
深入解析Android AIDL:实现跨进程通信的利器
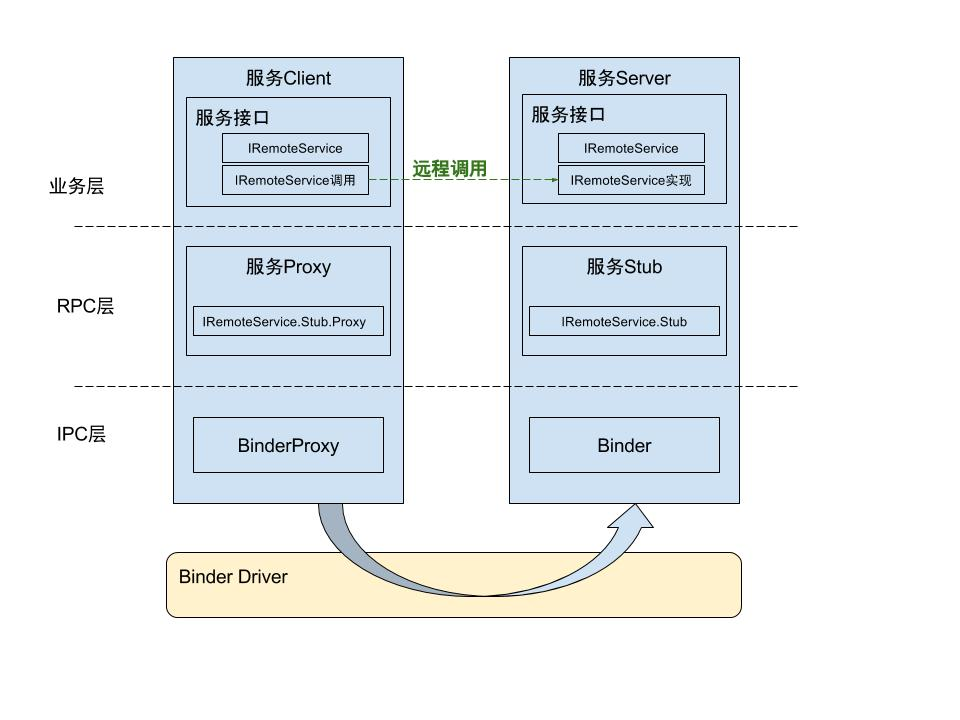
深入解析Android AIDL:实现跨进程通信的利器 1. 介绍Android AIDL Android Interface Definition Language (AIDL) 是一种Android系统中的跨进程通信机制。AIDL允许一个应用程序的组件与另一个应用程序的组件通信,并在两者之间传输数据。 AIDL的主要作…...

【笔记】Helm-5 Chart模板指南-14 下一步
下一步 本指南旨在为chart开发者提供对如何使用Helm模板语言的强大理解能力。该模板聚焦于模板开发的技术层面。 但涉及到chart的实际日常开发时,很多内容本指南并没有覆盖到。这里有一些有用的文档链接帮助您创建新的chart: CNCF的 Artifact Hub 是ch…...

axios 官网速通
前言:参考 AXIOS 中文文档 一 起步 1. 介绍 1.1 Axios 是什么? Axios 是一个基于 promise 网络请求库,作用于 node.js 和浏览器中。在服务端使用 node.js 的 http 模块, 在客户端 (浏览端) 使用 XMLHttpRequests。 1.2 安装 $ npm instal…...

luigi,一个好用的 Python 数据管道库!
🏷️个人主页:鼠鼠我捏,要死了捏的主页 🏷️付费专栏:Python专栏 🏷️个人学习笔记,若有缺误,欢迎评论区指正 前言 大家好,今天为大家分享一个超级厉害的 Python 库 - luigi。 Github地址:https://github.com/spotify/luigi 在大数据时代,处理海量数据已经成…...
用HTML5实现动画
用HTML5实现动画 要在HTML5中实现动画,可以使用以下几种方法:CSS动画、使用<canvas>元素和JavaScript来实现动画、使用JavaScript动画库。重点介绍前两种。 一、CSS动画 CSS3 动画:使用CSS3的动画属性和关键帧(keyframes&…...

【Linux笔记】进程间通信之管道
一、匿名管道 我们在之前学习进程的时候就知道了一个概念,就是进程间是互相独立的,所以就算是两个进程是父子关系,其中一个进程退出了也不会影响另一个进程。 也因为进程间是互相独立的,所以两个进程间就不能直接的传递信息或者…...
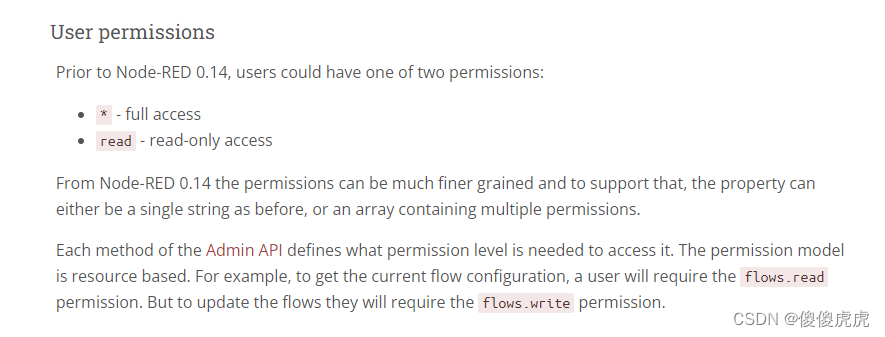
【Node-RED】安全登陆时,账号密码设置
【Node-RED】安全登陆时,账号密码设置 前言实现步骤密码生成setting.js 文件修改 安全权限 前言 Node-RED 在初始下载完成时,登录是无账号密码的。基于安全性考虑,本期博文介绍在安全登陆时,如何进行账号密码设置。当然ÿ…...
-k8s的服务发现机制)
Kubernetes基础(二十一)-k8s的服务发现机制
1 概述 Kubernetes(K8s)是一个强大的容器编排平台,提供了丰富的功能来简化容器化应用的管理。其中之一重要的特性就是服务发现机制,它使得应用程序能够在K8s集群中动态地发现和访问其他服务。本文将深入研究K8s中的服务发现机制&…...

华纳云:docker更新容器镜像的常用方法
更新 Docker 容器镜像可以通过以下几种方法实现: 1. 使用 docker pull 命令手动拉取更新的镜像: docker pull <镜像名>:<标签> 这会拉取指定镜像的最新版本或者指定标签的版本到本地。然后您可以停止并删除现有的容器,使用新的镜…...

什么时候会触发FullGC?描述一下JVM加载class文件的原理机制?
什么时候会触发 FullGC? 除直接调用 System.gc 外,触发 Full GC 执行的情况有如下四种。 1. 旧生代空间不足 旧生代空间只有 在新生代对象转入及创建为大对象、大数组时才会出现不足的现象,当执行 Full GC 后空间仍然不 足,则…...
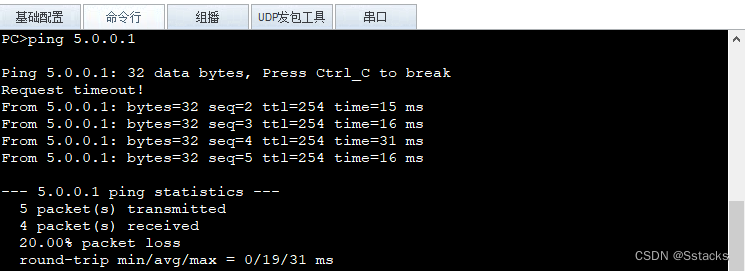
HCIP-MGRE实验配置、PPP的PAP认证与CHAP认证、MGRE、GRE网络搭建、NAT
实验要求 R5为ISP,只能进行IP地址配素,其所有地址均为公有IP地址R1和R5间使用PPP的PAP认证,R5为主认证方 R2与R5之间使用PPP的chap认证,R5为主认证方 R3与R5之间使用HDLC封装。R1/R2/R3构建一个MGRE环境,R1为中心站点;R1、R4间为…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
