图论之dfs与bfs的练习
dfs--深度优选搜索
bfs--广度优先搜索
迷宫问题--dfs
问题:
给定一个n*m的二维迷宫数组其中S是起点,T是终点,*是墙壁(无法通过), .是道路
问从起点S出发沿着上下左右四个方向走,能否走到T点?能输出"YES",否则输出"NO"。
8 8
*****...
*.S...**
*****.**
*****..*
*T..**.*
.**.**.*
..*....*
...*****
#include<iostream>
using namespace std;
const int N = 1e4 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int n, m;
int sx, sy, tx, ty;
bool flag;
void dfs(int px, int py) {//如果当前搜的点p是终点点t,终止搜索if (px == tx && py == ty) {flag = true;return;}//沿着点p的邻接点继续搜索for (int i = 0; i < 4; i++) {int bx=px+dx[i], by=py+dy[i];//生成邻接点if (bx<1 || bx>n || by<1 || by>m) continue;//迷宫图的边界if (g[bx][by] == '*') continue;//墙壁if (vis[bx][by]) continue;//走过的不再走vis[bx][by] = 1;dfs(bx, by);}
}
int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> g[i][j];if (g[i][j] == 'S') sx = i, sy = j;//找到起点的坐标if (g[i][j] == 'T') tx = i, ty = j;//找到终点的坐标}}vis[sx][sy] = 1;flag = false;dfs(sx, sy);if (flag) cout << "YES" << endl;else cout << "NO" << endl;return 0;
}
求迷宫问题的最短路--bfs
问题:
给定一个n*m的二维迷宫数组其中S是起点,T是终点,*是墙壁(无法通过), .是道路
问从起点S出发沿着上下左右四个方向走,能否走到T点?如果能打印最短路径长度,否则输出0。
8 8
*****...
*.S...**
*****.**
*****..*
*T..**.*
.**.**.*
..*....*
...*****
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e4 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int n, m;
int sx, sy, tx, ty;
struct point {int x, y, depth;
};
void bfs(point s) {queue<point> q;q.push(s); vis[s.x][s.y] = 1;while (!q.empty()) {point cur = q.front(); q.pop();if (cur.x == tx && cur.y == ty) {flag = true;cout << cur.depth - 1 << endl;return;}//通过方向数组找到cur的邻接点,沿着邻接点继续广搜for (int i = 0; i < 4; i++) {int bx = cur.x + dx[i], by = cur.y + dy[i];//生成邻接点if (bx<1 || bx>n || by<1 || by>m) continue;if (g[bx][by] == '*') continue;if (vis[bx][by]) continue;vis[bx][by] = 1;q.push({ bx,by,cur.depth + 1 });}}
}
int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> g[i][j];if (g[i][j] == 'S') sx = i, sy = j;if (g[i][j] == 'T') tx = i, ty = j;}}vis[sx][sy] = 1;flag = false;bfs({ sx, sy ,1});return 0;
}
1215:迷宫
信息学奥赛一本通(C++版)在线评测系统
【题目描述】
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由n×n�×�的格点组成,每个格点只有22种状态,
.和#,前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点A走到点B,问在不走出迷宫的情况下能不能办到。如果起点或者终点有一个不能通行(为#),则看成无法办到。【输入】
第1行是测试数据的组数k�,后面跟着k�组输入。每组测试数据的第11行是一个正整数n(1≤n≤100)�(1≤�≤100),表示迷宫的规模是n×n�×�的。接下来是一个n×n�×�的矩阵,矩阵中的元素为
.或者#。再接下来一行是44个整数ha,la,hb,lbℎ�,��,ℎ�,��,描述A处在第haℎ�行, 第la��列,B处在第hbℎ�行, 第lb��列。注意到ha,la,hb,lbℎ�,��,ℎ�,��全部是从00开始计数的。【输出】
k�行,每行输出对应一个输入。能办到则输出“YES”,否则输出“NO”。
【输入样例】
2 3 .## ..# #.. 0 0 2 2 5 ..... ###.# ..#.. ###.. ...#. 0 0 4 0【输出样例】
YES NO
解法一:dfs
#include<iostream>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//标记数组
int t,n, sx, sy, tx, ty;
//方向数组
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool flag;
void dfs(int px, int py) {if (px == tx && py == ty) {flag = true;return;}//沿着邻接点继续搜索for (int i = 0; i < 4; i++) {int bx = px + dx[i], by = py + dy[i];if (bx<1 || bx>n || by<1 || by>n) continue;if (g[bx][by] == '#') continue;if (vis[bx][by]) continue;//如果以上情况均不成立,证明邻接点有效,沿着该邻接点继续深搜vis[bx][by] = 1;//不标记会报栈溢出错误dfs(bx, by);}
}
int main() {cin >> t;while (t--) {cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)cin >> g[i][j]; cin >> sx >> sy >> tx >> ty;sx++, sy++, tx++, ty++;//注意:本题下标从0开始//多组数据要将相关状态重置flag = false;memset(vis, 0, sizeof vis);//将vis数组全体清0vis[sx][sy] = 1;dfs(sx, sy);if (flag) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}
解法二:bfs
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//标记数组
int t, n, sx, sy, tx, ty;
//方向数组
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool flag;
struct point {int x, y;
};
void bfs(point p) {queue<point> q;q.push(p); vis[p.x][p.y] = 1;while (!q.empty()) {point cur=q.front(); q.pop();if (cur.x == tx && cur.y== ty) {flag = true;return;}//沿着邻接点继续搜索for (int i = 0; i < 4; i++) {int bx = cur.x + dx[i], by = cur.y + dy[i];if (bx<1 || bx>n || by<1 || by>n) continue;if (g[bx][by] == '#') continue;if (vis[bx][by]) continue;//如果以上情况均不成立,证明邻接点有效,沿着该邻接点继续深搜vis[bx][by] = 1;q.push({ bx,by });}}
}
int main() {cin >> t;while (t--) {cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)cin >> g[i][j]; /*scanf(" %c", &g[i][j]); */cin >> sx >> sy >> tx >> ty;sx++, sy++, tx++, ty++;//注意本题下标从0开始//多组数据要将相关状态重置flag = false;memset(vis, 0, sizeof vis);//将vis数组全体清0vis[sx][sy] = 1;bfs({sx, sy});if (flag) cout << "YES" << endl;else cout << "NO" << endl;}return 0;
}
1216:红与黑
【题目描述】
有一间长方形的房子,地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上,只能向相邻的黑色瓷砖移动。请写一个程序,计算你总共能够到达多少块黑色的瓷砖。
【输入】
包括多组数据。每组数据的第一行是两个整数W和H,分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中,每行包括W个字符。每个字符表示一块瓷砖的颜色,规则如下:
1)‘.’:黑色的瓷砖;
2)‘#’:红色的瓷砖;
3)‘@’:黑色的瓷砖,并且你站在这块瓷砖上。该字符在每组数据中唯一出现一次。
当在一行中读入的是两个零时,表示输入结束。
【输出】
对每组数据,分别输出一行,显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。
【输入样例】
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 0 0【输出样例】
45
解法一:dfs
#include<iostream>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int sx, sy;
int w, h;
int cnt;
void dfs(int px,int py)
{//沿着邻接点搜索for (int i = 0; i < 4; i++){int bx = px + dx[i], by = py + dy[i];if (g[bx][by] == '#')continue;if (bx<1 || bx>w || by<1 || by>h)continue;if (vis[bx][by])continue;vis[bx][by] = 1;cnt++;dfs(bx, by);}
}int main()
{/*注意:本题是先输入列再输入行*/while (cin >> h >> w && w && h)//注意要判断w和h都为0结束{for (int i = 1; i <= w; i++){for (int j = 1; j <= h; j++){cin >> g[i][j];if (g[i][j] == '@')sx = i, sy = j;}}//多组数据注意相关状态cnt = 1;memset(vis, 0, sizeof vis);//vis数组全体清0vis[sx][sy] = 1;dfs(sx, sy);cout << cnt << endl;}return 0;
}解法二:bfs
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int sx, sy;
int w, h;
int cnt;
struct point
{int x, y;
};
void dfs(point s)
{queue<point>q;q.push(s); vis[s.x][s.y] = 1;while (!q.empty()) {point cur = q.front(); q.pop();//沿着邻接点搜索for (int i = 0; i < 4; i++){int bx = cur.x + dx[i], by = cur.y + dy[i];if (g[bx][by] == '#')continue;if (bx<1 || bx>w || by<1 || by>h)continue;if (vis[bx][by])continue;vis[bx][by] = 1;cnt++;q.push({bx,by});}}
}int main()
{/*注意:本题是先输入列再输入行*/while (cin >> h >> w && w && h)//注意要判断w和h都为0结束{for (int i = 1; i <= w; i++){for (int j = 1; j <= h; j++){cin >> g[i][j];if (g[i][j] == '@')sx = i, sy = j;}}//多组数据注意相关状态cnt = 1;memset(vis, 0, sizeof vis);//vis数组全体清0vis[sx][sy] = 1;dfs({ sx, sy });cout << cnt << endl;}return 0;
}1219:马走日--dfs
注意:本题需要用到回溯算法,故只能用深度优先搜索
【题目描述】
马在中国象棋以日字形规则移动。
请编写一段程序,给定n×m大小的棋盘,以及马的初始位置(x,y),要求不能重复经过棋盘上的同一个点,计算马可以有多少途径遍历棋盘上的所有点。
【输入】
第一行为整数T(T < 10),表示测试数据组数。
每一组测试数据包含一行,为四个整数,分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。
【输出】
每组测试数据包含一行,为一个整数,表示马能遍历棋盘的途径总数,0为无法遍历一次。
【输入样例】
1 5 4 0 0【输出样例】
32
#include<iostream>
using namespace std;
const int N = 1e2 + 10;
int g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组--八个方向
int dx[] = { 1,1,-1,-1,2,2,-2,-2 };
int dy[] = { 2,-2,2,-2,1,-1,1,-1};
int t; int n, m,sx,sy;
int cnt;
void dfs(int px, int py, int depth)
{if (depth == n * m)//按照此时的搜索方案已经搜完整个棋盘了{cnt++;return;}for (int i = 0; i < 8; i++)/*注意:八个方向*/{int bx = px + dx[i], by = py + dy[i];if (vis[bx][by])continue;if (bx<1 || bx>n || by<1 || by>m)continue;vis[bx][by] = 1;dfs(bx, by,depth+1);//回溯vis[bx][by] = 0;}}
int main()
{cin >> t;while (t--){cin >> n >> m;//多组数据相关状态清空cnt =0;cin >> sx >> sy;sx++, sy++;memset(vis, 0, sizeof vis);vis[sx][sy] = 1;dfs(sx, sy,1);//起点是第一层,最后应该走到n*m层结束cout << cnt << endl;}return 0;
}1212:LETTERS--dfs
【题目描述】
给出一个row×col���×���的大写字母矩阵,一开始的位置为左上角,你可以向上下左右四个方向移动,并且不能移向曾经经过的字母。问最多可以经过几个字母。
【输入】
第一行,输入字母矩阵行数R�和列数S�,1≤R,S≤201≤�,�≤20。
接着输出R�行S�列字母矩阵。
【输出】
最多能走过的不同字母的个数。
【输入样例】
3 6 HFDFFB AJHGDH DGAGEH【输出样例】
6
#include<iostream>
using namespace std;
char g[N][N];
bool vis[N];
int dx[] = { 1,-1,0,0};
int dy[] = { 0,0,1,-1};
int n, m;
int ans = 0;
void dfs(int px,int py,int depth)
{ans = max(ans, depth);//选取经过字母数最多的for (int i = 0; i < 4; i++){int bx = px + dx[i], by = py + dy[i];if (vis[g[bx][by]])continue;if (bx<1 || bx>n || by<1 || by>m) continue;vis[g[bx][by]] = 1;dfs(bx, by, depth + 1);vis[g[bx][by]] =0;//回溯}
}
int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> g[i][j];}}vis[g[1][1]] = 1;dfs(1,1,1);cout << ans;return 0;
}求最短路径
1251:仙岛求药--bfs
【题目描述】
少年李逍遥的婶婶病了,王小虎介绍他去一趟仙灵岛,向仙女姐姐要仙丹救婶婶。叛逆但孝顺的李逍遥闯进了仙灵岛,克服了千险万难来到岛的中心,发现仙药摆在了迷阵的深处。迷阵由M×N个方格组成,有的方格内有可以瞬秒李逍遥的怪物,而有的方格内则是安全。现在李逍遥想尽快找到仙药,显然他应避开有怪物的方格,并经过最少的方格,而且那里会有神秘人物等待着他。现在要求你来帮助他实现这个目标。
下图 显示了一个迷阵的样例及李逍遥找到仙药的路线。
【输入】
输入有多组测试数据. 每组测试数据以两个非零整数 M 和 N 开始,两者均不大于20。M 表示迷阵行数, N 表示迷阵列数。接下来有 M 行, 每行包含N个字符,不同字符分别代表不同含义:
1)‘@’:少年李逍遥所在的位置;
2)‘.’:可以安全通行的方格;
3)‘#’:有怪物的方格;
4)‘*’:仙药所在位置。
当在一行中读入的是两个零时,表示输入结束。
【输出】
对于每组测试数据,分别输出一行,该行包含李逍遥找到仙药需要穿过的最少的方格数目(计数包括初始位置的方块)。如果他不可能找到仙药, 则输出 -1。
【输入样例】
8 8 .@##...# #....#.# #.#.##.. ..#.###. #.#...#. ..###.#. ...#.*.. .#...### 6 5 .*.#. .#... ..##. ..... .#... ....@ 9 6.#..#. .#.*.# .####. ..#... ..#... ..#... ..#... #.@.## .#..#. 0 0【输出样例】
10
8
-1
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
int n, m,sx,sy,tx,ty;
char g[N][N];
bool vis[N][N];
int ans = -1;
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
struct point { int x, y, depth; };
void bfs(point p) {queue<point> q;q.push(p); vis[p.x][p.y] = 1;while (!q.empty()) {point cur = q.front(); q.pop();if (cur.x == tx && cur.y == ty) {ans= cur.depth - 1;return;}for (int i = 0; i < 4; i++) {int bx = cur.x + dx[i], by = cur.y + dy[i];if (bx<1 || bx>n || by<1 || by>m) continue;if (vis[bx][by]) continue;if (g[bx][by] == '#') continue;vis[bx][by] = 1;q.push({ bx,by,cur.depth + 1 });}}
}
int main() {while (cin >> n >> m && n && m) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> g[i][j];if (g[i][j] == '@') sx = i, sy = j;if (g[i][j] == '*') tx = i, ty = j;}}ans = -1;memset(vis, 0, sizeof vis);bfs({ sx,sy,1 });cout << ans << endl;}return 0;
}
1330:【例8.3】最少步数--bfs
【题目描述】
在各种棋中,棋子的走法总是一定的,如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性,因此,他规定马既能按“日”走,也能如象一样走“田”字。他的同桌平时喜欢下围棋,知道这件事后觉得很有趣,就想试一试,在一个(100×100)的围棋盘上任选两点A、B,A点放上黑子,B点放上白子,代表两匹马。棋子可以按“日”字走,也可以按“田”字走,俩人一个走黑马,一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时,谁获胜。现在他请你帮忙,给你A、B两点的坐标,想知道两个位置到(1,1)点可能的最少步数。
【输入】
A、B两点的坐标。
【输出】
最少步数。
【输入样例】
12 16 18 10【输出样例】
8 9
#include<iostream>
#include<queue>
const int N = 1e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {1,1,-1,-1,2,2,-2,-2,2,2,-2,-2};
int dy[] = {2,-2,2,-2,1,-1,1,-1,2,-2,2,-2};
int n, m;
int sx, sy;
int ans;
struct point
{int x, y,depth;
};
void bfs(point s)
{queue<point>q;q.push(s); vis[s.x][s.y] = 1;while (!q.empty()){point cur = q.front(); q.pop();if (cur.x == 1 && cur.y == 1){ans=cur.depth - 1 ;return;}for (int i = 0; i < 12; i++){int bx = cur.x + dx[i], by = cur.y + dy[i];if (bx<1 || bx>100 || by<1 || by>100)continue;if (vis[bx][by])continue;//注意,搜索时也不能搜0vis[bx][by] = 1;q.push({ bx, by,cur.depth+1});}}
}int main()
{int t = 2;while (t--){ans = 0;cin >> sx>>sy;memset(vis, 0, sizeof vis);bfs({ sx, sy ,1});cout << ans<<endl;}return 0;
}1255:迷宫问题--bfs
【题目描述】
定义一个二维数组:
int maze[5][5] = { 0,1,0,0,0, 0,1,0,1,0, 0,0,0,0,0, 0,1,1,1,0, 0,0,0,1,0, };它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
【输入】
一个5 × 5的二维数组,表示一个迷宫。数据保证有唯一解。
【输出】
左上角到右下角的最短路径,格式如样例所示。
【输入样例】
0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0【输出样例】
(0, 0) (1, 0) (2, 0) (2, 1) (2, 2) (2, 3) (2, 4) (3, 4) (4, 4)
#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
struct point
{int x, y;
};
point path[N][N];
void bfs(point s)
{queue<point>q;q.push(s); vis[s.x][s.y] = 1;while (!q.empty()){point cur = q.front(); q.pop();if (cur.x == 5 && cur.y == 5)return;for (int i = 0; i < 4; i++){int bx = cur.x + dx[i], by = cur.y + dy[i];if (bx < 1 || bx>5 || by < 1 || by>5)continue;if (g[bx][by] == '1')continue;if (vis[bx][by])continue;vis[bx][by] = 1;path[bx][by] = cur;q.push({bx, by});}}
}
void print(int px,int py)
{if (px == 0 && py == 0)return;print(path[px][py].x, path[px][py].y);printf("(%d, %d)\n", px-1, py-1);
}
int main()
{for (int i = 1; i <= 5; i++)for (int j = 1; j <= 5; j++)cin >> g[i][j];bfs({1,1});print(5,5);return 0;
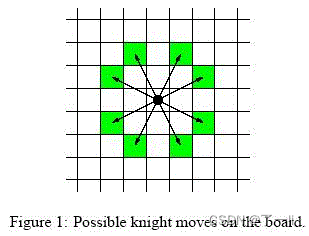
} 1257:Knight Moves【题目描述】 输入n�代表有个n×n�×�的棋盘,输入开始位置的坐标和结束位置的坐标,问一个骑士朝棋盘的八个方向走马字步,从开始坐标到结束坐标可以经过多少步。 【输入】 首先输入一个n�,表示测试样例的个数。 每个测试样例有三行。 第一行是棋盘的大小L(4≤L≤300)�(4≤�≤300); 第二行和第三行分别表示马的起始位置和目标位置(0..L−1)(0..�−1)。 【输出】 马移动的最小步数,起始位置和目标位置相同时输出00。 【输入样例】 3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1 【输出样例】 5
28
0 |
#include<iostream>
#include<queue>
//#include<Windows.h>//动画演示
using namespace std;
const int N = 3e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {1,1,2,2,-1,-1,-2,-2};
int dy[] = {2,-2,1,-1,2,-2,1,-1};
int t;
int n,sx, sy, tx, ty;
int ans;
struct point { int x; int y; int depth; };
void dfs(point s)
{queue<point>q;q.push(s); vis[s.x][s.y] = 1;while (!q.empty()){point cur = q.front(); q.pop();if (cur.x == tx && cur.y == ty){ans = cur.depth-1;return;}for (int i = 0; i < 8; i++){int bx = cur.x + dx[i], by = cur.y + dy[i];if (bx<1 || bx> n || by<1 || by>n) continue;if (vis[bx][by]) continue;vis[bx][by] = 1;q.push({ bx, by,cur.depth+1 });}}}int main()
{cin >> t;while (t--){cin >> n;cin >> sx >> sy >> tx >> ty;sx++, sy++,tx++, ty++;ans = 0;memset(vis, 0, sizeof vis);dfs({ sx, sy,1 });cout << ans<<endl;}return 0;
}相关文章:
图论之dfs与bfs的练习
dfs--深度优选搜索 bfs--广度优先搜索 迷宫问题--dfs 问题: 给定一个n*m的二维迷宫数组其中S是起点,T是终点,*是墙壁(无法通过), .是道路 问从起点S出发沿着上下左右四个方向走,能否走到T点&a…...

Vue练习5:图片的引入
后续会补充 1.require引入 src -> asstes <template><img :src"url"> </template><script> export default {name: App,data(){return{url: require("./assets/logo.png"),}} } </script> 2.import引入 src…...

SpringBoot+Kafka
文章目录 一、依赖二、配置文件三、API1、生产者2、消费者 一、依赖 <!-- spring-kafka(与kafka的版本一致) --> <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId>…...

世界顶级名校计算机专业,都在用哪些书当教材?(文末送书)
目录 01《深入理解计算机系统》02《算法导论》03《计算机程序的构造和解释》04《数据库系统概念》05《计算机组成与设计:硬件/软件接口》06《离散数学及其应用》07《组合数学》08《斯坦福算法博弈论二十讲》参与规则 清华、北大、MIT、CMU、斯坦福的学霸们在新学期里…...
)
蓝桥杯刷题--python-8(2023 填空题)
0幸运数 - 蓝桥云课 (lanqiao.cn) res=0 for i in range (1,100000000):l_n=[]for j in str(i):l_n.append(int(j))if len(l_n) % 2 ==0:cur =len(l_n)>>1if sum(l_n[:cur])==sum(l_n[cur:]):res+=1 print(res) 0有奖问答 - 蓝桥云课 (lanqiao.cn) dfs def bfs(score, q…...

Eclipse - Reset Perspective
Eclipse - Reset Perspective 1. Window -> Perspective -> Reset Perspective2. Reset Perspective -> YesReferences 1. Window -> Perspective -> Reset Perspective 2. Reset Perspective -> Yes References [1] Yongqiang Cheng, https://yo…...

1.5v的电池电压低于多少v等于没电
对于1.5V的电池,电压低于一定值时就不再适合使用了。具体的电压值取决于电池的类型和使用设备的需求。一般来说, 对于接收设备(如收音机、BB机、遥控机等),每节电池电压一般到1.2V以下就认为没电了。有些电动玩具、剃…...
LabVIEW智能监测系统
LabVIEW智能监测系统 设计与实现一个基于LabVIEW的智能监测系统,通过高效的数据采集和处理能力,提高监测精度和响应速度。系统通过集成传感器技术与虚拟仪器软件,实现对环境参数的实时监测与分析,进而优化监控过程,提…...

代码随想录刷题第34天
第一题是柠檬水找零https://leetcode.cn/problems/lemonade-change/,感觉并没有特别靠近贪心算法,可供讨论的情况非常少,5元收下,10元返5元,20元返15元,对各种找零情况讨论一下即可。 class Solution { pu…...

AMD FPGA设计优化宝典笔记(5)低频全局复位与高扇出
亚军老师的这本书《AMD FPGA设计优化宝典》,他主要讲了两个东西: 第一个东西是代码的良好风格; 第二个是设计收敛等的本质。 这个书的结构是一个总论,加上另外的9个优化,包含的有:时钟网络、组合逻辑、触发…...
14. Qt 程序菜单实现,基于QMainWindow
目录 前言: 技能: 内容: 一、ui中直接添加控件实现 二、 完全通过代码实现菜单 参考: 前言: 基于QMainWindow,两种方式实现菜单:通过直接添加ui控件快速添加菜单和完全通过代码实现菜单&a…...
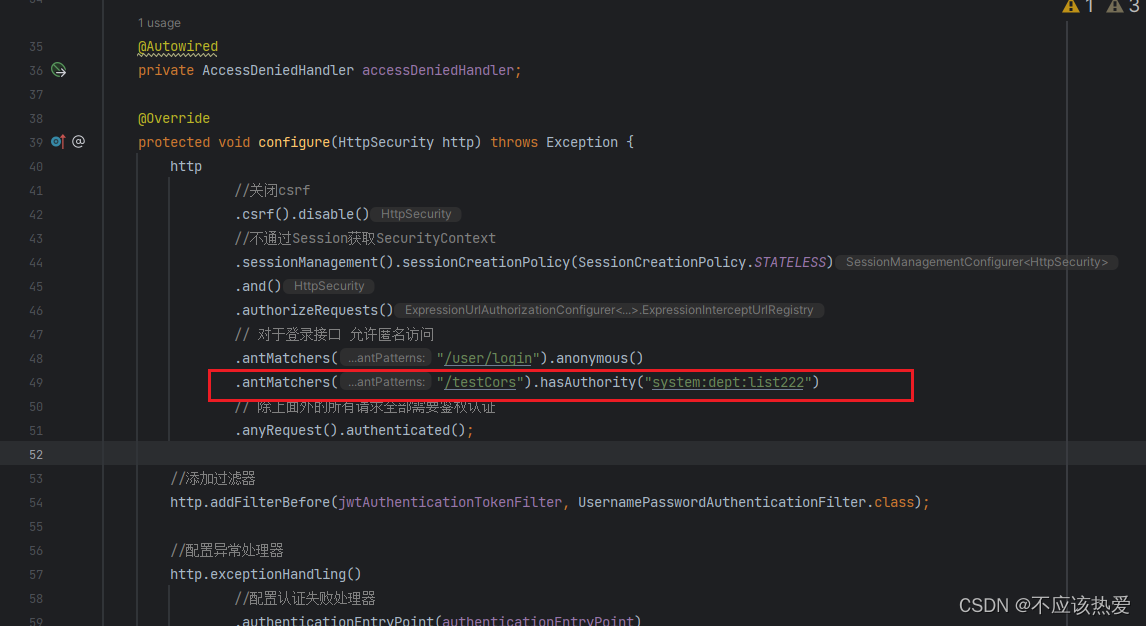
如何利用SpringSecurity进行认证与授权
目录 一、SpringSecurity简介 1.1 入门Demo 二、认证 编辑 2.1 SpringSecurity完整流程 2.2 认证流程详解 2.3 自定义认证实现 2.3.1 数据库校验用户 2.3.2 密码加密存储 2.3.3 登录接口实现 2.3.4 认证过滤器 2.3.5 退出登录 三、授权 3.1 权限系统作用 3.2 授…...

如何简单上手清华AutoGPT并搭建到本地环境
一、准备工作 安装Docker:确保你的本地机器上已经安装了Docker。如果还没有安装,请访问Docker官方网站并按照指引进行安装。--点击进入Docker官网 获取清华AutoGPT的Docker镜像:清华AutoGPT团队可能已经提供了一个Docker镜像,方便…...
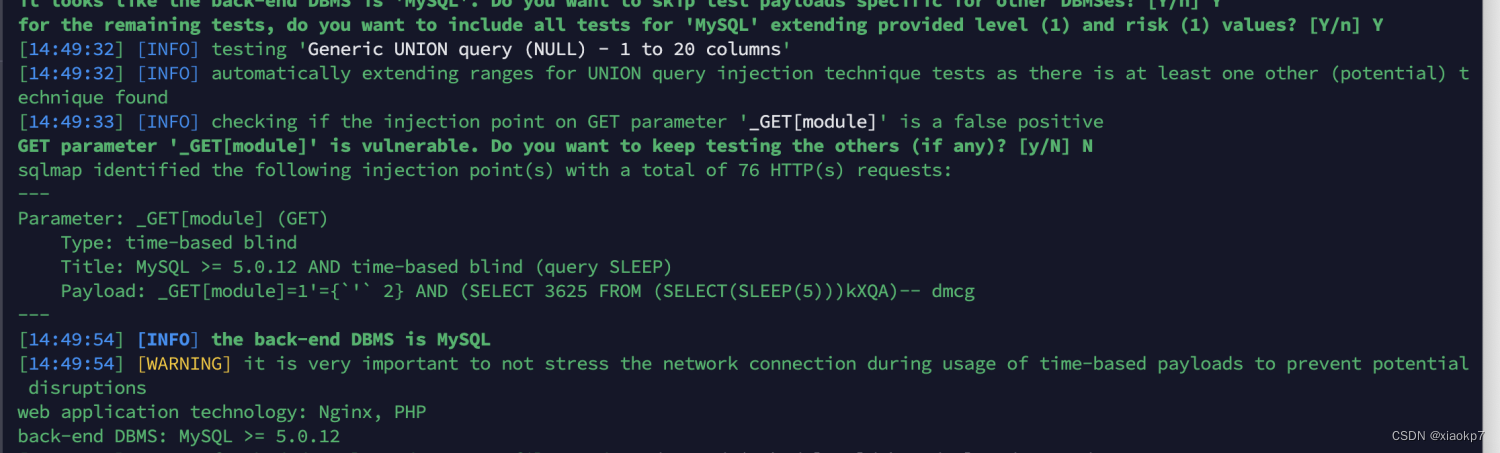
【漏洞复现-通达OA】通达OA share存在前台SQL注入漏洞
一、漏洞简介 通达OA(Office Anywhere网络智能办公系统)是由北京通达信科科技有限公司自主研发的协同办公自动化软件,是与中国企业管理实践相结合形成的综合管理办公平台。通达OA为各行业不同规模的众多用户提供信息化管理能力,包…...

HTML5 Canvas与JavaScript携手绘制动态星空背景
目录 一、程序代码 二、代码原理 三、运行效果 一、程序代码 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>星空背景</title> </head> <body style"overflow-x:hidden;"><canvas …...

如何优雅地与ChatGPT对话?
ChatGPT已经发布了一年之久了,但你真的会使用ChatGPT吗?同一个问题,不同的问法得到的答案可能千差万别,你可以把ChatGPT当作一个知识面很广的专家,他上知天文下知地理,但他无法直接知道你的意图,…...

AI提示工程实战:从零开始利用提示工程学习应用大语言模型【文末送书-19】
文章目录 背景什么是提示工程?从零开始:准备工作设计提示调用大语言模型 实际应用示例文字创作助手代码生成持续优化与迭代数据隐私与安全性可解释性与透明度总结 AI提示工程实战:从零开始利用提示工程学习应用大语言模型【文末送书-19】⛳粉…...
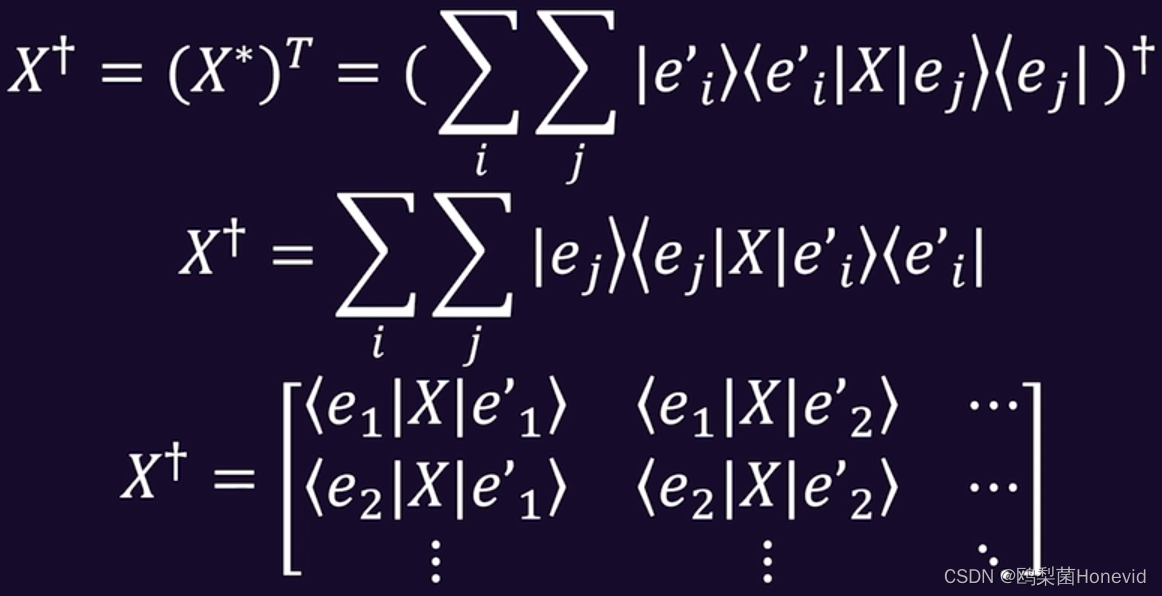
量子算法入门——3.狄拉克符号与量子态(3)
3. 狄拉克符号的数学基础 左矢是右矢的共轭转置 上标*表示共轭 算符就是对狄拉克符号进行操作,就是相当于矩阵操作向量,算符对应本征值和本征态 本征值:拉伸x、y向量的程度本征态:x、y向量 上标匕首🗡符号…...
list)
c++ STL系列——(三)list
目录 引言 list的特点 list的用法 list与其他容器的比较 结论 引言 在C STL中,list 是一个非常灵活且功能强大的双向链表容器,它允许存储任意类型的元素,并提供了丰富的操作函数,包括插入、删除、排序、查找以及对容器的遍历…...

软考29-上午题-排序
一、排序的基本概念 1-1、稳定性 稳定性指的是相同的数据所在的位置经过排序后是否发生变化。若是排序后,次序不变,则是稳定的。 1-2、归位 每一趟排序能确定一个元素的最终位置。 1-3、内部排序 排序记录全部存放在内存中进行排序的过程。 1-4、外部…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...