代码随想录算法训练营29期|day54 任务以及具体安排
第九章 动态规划part11
- 123.买卖股票的最佳时机III

// 版本一 class Solution {public int maxProfit(int[] prices) {int len = prices.length;// 边界判断, 题目中 length >= 1, 所以可省去if (prices.length == 0) return 0;/** 定义 5 种状态:* 0: 没有操作, 1: 第一次买入, 2: 第一次卖出, 3: 第二次买入, 4: 第二次卖出*/int[][] dp = new int[len][5];dp[0][1] = -prices[0];// 初始化第二次买入的状态是确保 最后结果是最多两次买卖的最大利润dp[0][3] = -prices[0];for (int i = 1; i < len; i++) {dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);}return dp[len - 1][4];} }思路:于上两个股票买卖问题的区别在于这道题限制了买卖次数,需要定义五种状态:0、1、2、3、4来代表不同的状态。然后使用递推公式对dp数组进行更新。
- 188.买卖股票的最佳时机IV

// 版本一: 三维 dp数组 class Solution {public int maxProfit(int k, int[] prices) {if (prices.length == 0) return 0;// [天数][交易次数][是否持有股票]int len = prices.length;int[][][] dp = new int[len][k + 1][2];// dp数组初始化// 初始化所有的交易次数是为确保 最后结果是最多 k 次买卖的最大利润for (int i = 0; i <= k; i++) {dp[0][i][1] = -prices[0];}for (int i = 1; i < len; i++) {for (int j = 1; j <= k; j++) {// dp方程, 0表示不持有/卖出, 1表示持有/买入dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);}}return dp[len - 1][k][0];} }// 版本二: 二维 dp数组 class Solution {public int maxProfit(int k, int[] prices) {if (prices.length == 0) return 0;// [天数][股票状态]// 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作int len = prices.length;int[][] dp = new int[len][k*2 + 1];// dp数组的初始化, 与版本一同理for (int i = 1; i < k*2; i += 2) {dp[0][i] = -prices[0];}for (int i = 1; i < len; i++) {for (int j = 0; j < k*2 - 1; j += 2) {dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}return dp[len - 1][k*2];} }思路:该题与上题的区别在于该题是至多能k次,所以二维数组需要2*k+1的维度,1、3、5等奇数代表持有股票,2、4、6等偶数代表不持有股票。然后根据递推公式进行遍历递推。再进行dp数组的初始化。
相关文章:

代码随想录算法训练营29期|day54 任务以及具体安排
第九章 动态规划part11 123.买卖股票的最佳时机III // 版本一 class Solution {public int maxProfit(int[] prices) {int len prices.length;// 边界判断, 题目中 length > 1, 所以可省去if (prices.length 0) return 0;/** 定义 5 种状态:* 0: 没有操作, 1: 第一次买入…...

文件操作相关工具类
目录 1. 文件上传工具类 -- FileUploadUtils 2. 文件处理工具类 -- FileUtils 3. 媒体类型工具类 -- MimeTypeUtils 1. 文件上传工具类 -- FileUploadUtils /*** 文件上传工具类**/ public class FileUploadUtils {private static final Logger log LoggerFactory.ge…...
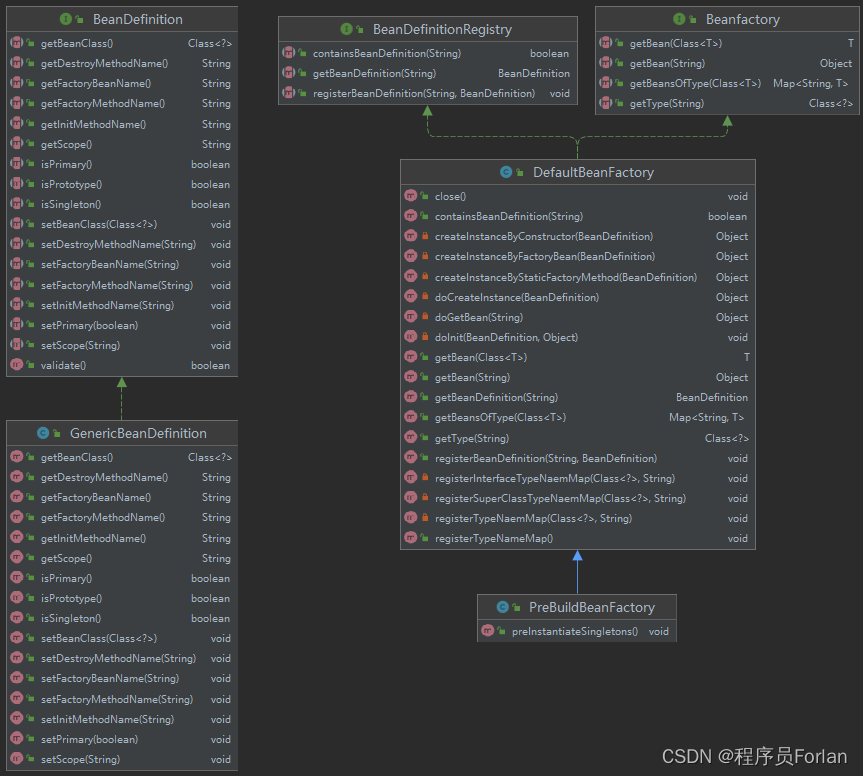
Spring源码:手写SpringIOC
文章目录 一、分析二、实现1、版本1:实现Bean注入IOC容器,并从容器中获取1)定义BeanDefinition2)定义BeanDefinition实现类3)定义BeanDefinitionRegistry4)定义Beanfactory5)定义默认Beanfactor…...
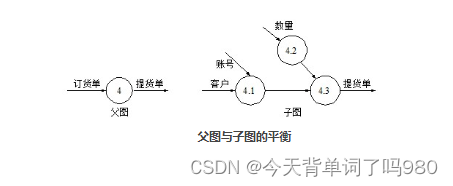
【软件设计师】程序猿需掌握的技能——数据流图
作为一个程序员,不仅要具备高水平的程序编码能力,还要是熟练掌握软件设计的方法和技术,具有一定的软件设计能力,一般包括软件分析设计图(常见的有数据流图,程序流程图,系统流程图,E-…...

17.3.1 像素处理
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 17.3.1 像素处理 C#处理图像,主要使用到Bitmap 类的 GetPixel方法和SetPixel方法。 Bitmap.GetPixel 方法:…...

白话微机:8.解释FPGA以及一些考研面试问题
一. 前言(更新世界观) 在“微机世界”,普通的城市(单片机)里,人又有一个别的名字叫做“数据”,人有0有1;人们也有住房,这些住房在这个世界叫做“存储器”;地上有路,这些路…...
-k8s存储对象Persistent Volume)
Kubernetes基础(十八)-k8s存储对象Persistent Volume
1 什么是Persistent Volume? 在容器化应用中,Pod的生命周期是短暂的,当Pod终止时,其中的数据通常也会被销毁。为了解决这个问题,Kubernetes引入了Persistent Volume(PV)的概念。PV是集群中的一…...

用linux命令将文本格式文件转换为csv文件
文章目录 前言例: 总结 前言 用到linux命令awk 使用 awk 命令来将文本文件转换为 CSV 格式。假设你有一个以空格或制表符分隔的文本文件,以下是将其转换为 CSV 格式的命令: awk BEGIN { OFS"," } { print $1, $2, $3 } input.txt > outpu…...

C++中的binary_search函数详解
C中的std::binary_search函数详解 在C标准模板库(STL)中,std::binary_search是一个非常有用的函数,它可以在一个已排序的序列中查找一个特定的元素。这个函数的使用非常直观,但是了解其工作原理和一些注意事项可以帮助…...

程序员为什么不喜欢关电脑?我来回答
程序员为什么不喜欢关电脑? 主题: 你是否注意到,程序员们似乎从不关电脑?别以为他们是电脑上瘾,实则是有他们自己的原因!让我们一起揭秘背后的原因,看看程序员们真正的“英雄”本色!…...
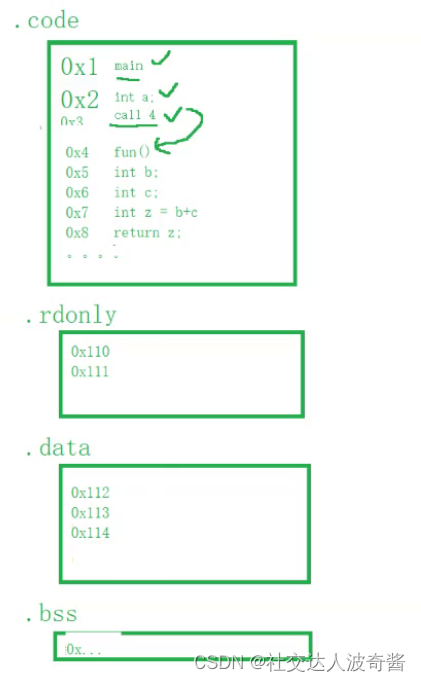
波奇学Linux:动静态库
创建静态库 Makefile文件 mymath.c文件 mymath.h文件 编译main.c文件 gcc 编译时会把在系统目录中寻找头文件和库文件,文件不在系统目录中用参数 -I 头文件所在文件夹/ -L 库的地址文件夹 -l除去lib和后缀。 拷贝文件到系统目录即可不用参数 库的安装类似于把头文件…...

1723. 完成所有工作的最短时间
文章目录 题意思路代码 题意 题目链接 K个工人,一共jobs个任务,问怎样分配任务,最短的最长工人完成任务完成时间。 思路 DFS剪枝(最大单个工人jobs时间超过ans时间;有限空闲工人拿任务)模拟退火dp 代码…...
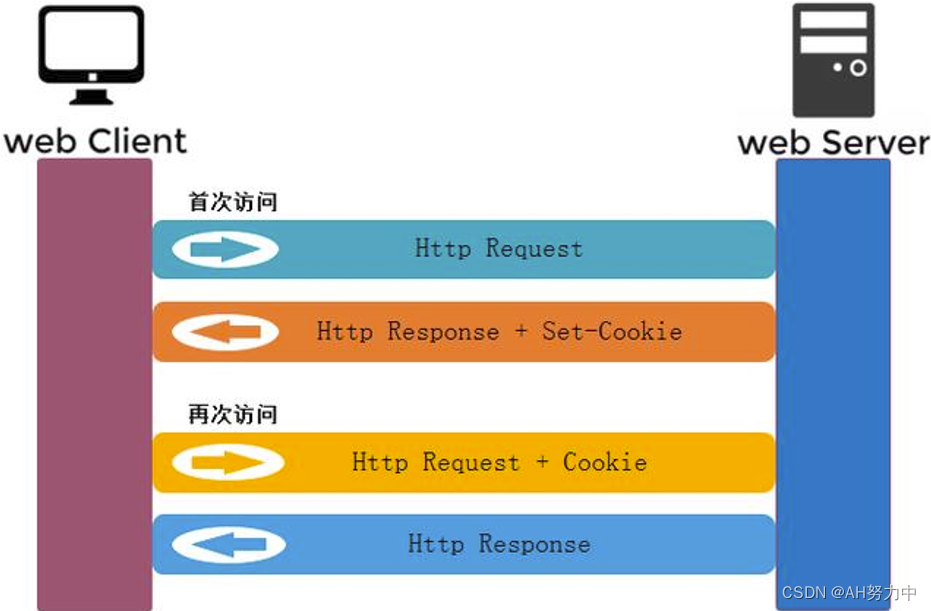
初始HTTP协议
一、http协议 1、http相关概念 互联网:是网络的网络,是所有类型网络的母集因特网:世界上最大的互联网网络。即因特网概念从属于互联网概念。习惯上,大家把连接在因特网上的计算机都成为主机。万维网:WWW(…...
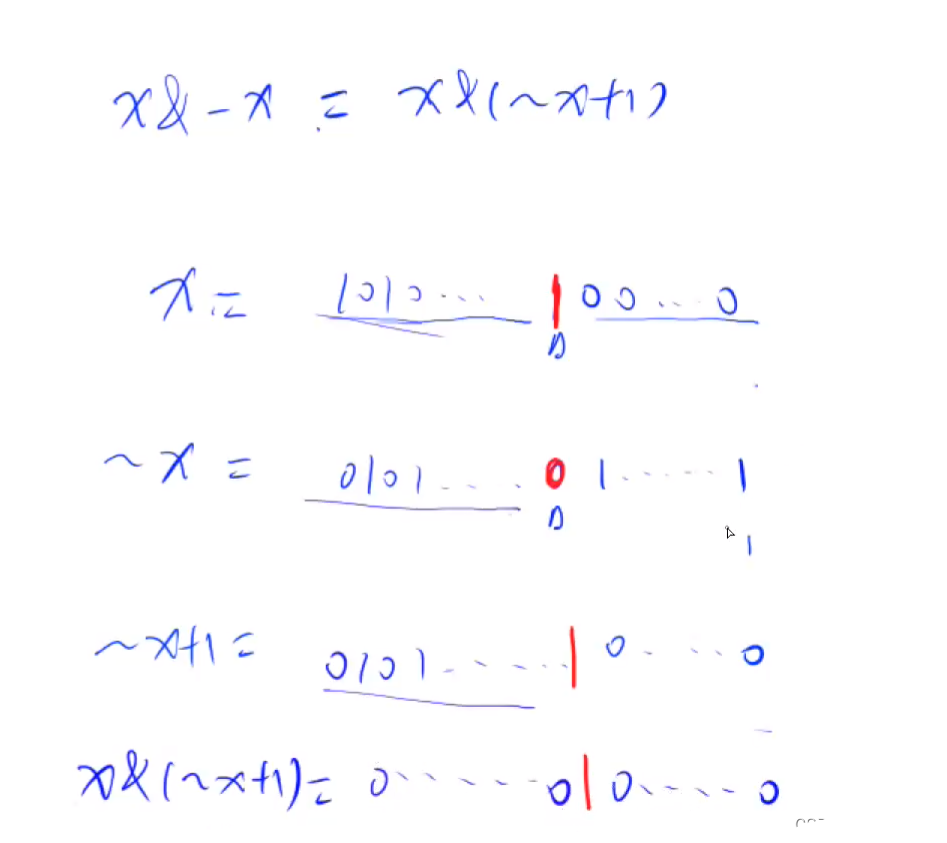
C++ 位运算常用操作 二进制中1的个数
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数。 输入格式 第一行包含整数 n 。 第二行包含 n 个整数,表示整个数列。 输出格式 共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表…...

大数据领域的数据仓库
在大数据领域,数据仓库(Data Warehouse)是一个用于存储、管理和分析大量数据的集中式系统。它从多个异构数据源收集数据,对数据进行清洗、转换和整合,然后将其存储在一个集中的位置,以支持复杂的查询、报告…...
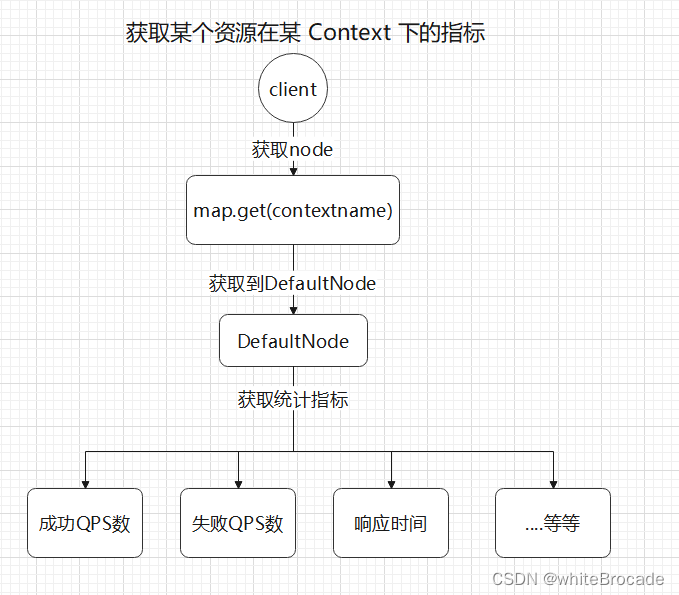
sentinel的资源数据指标是如何采集
资源数据采集 之前的NodeSelectorSlot和ClusterBuilderSlot已经完成了对资源调用树的构建, 现在则是要对资源进行收集, 核心点就是这些资源数据是如何统计 LogSlot 作用: 记录异常请求日志, 用于故障排查 public class LogSlot extends AbstractLinkedProcessorSlot<Def…...
算法刷题:找到字符串中所有的字母异位词
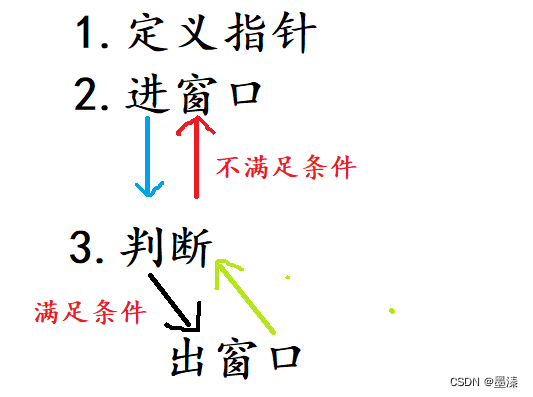
找到字符串中所有的字母异位词 .题目链接题目详情题目解析算法原理滑动窗口流程图定义指针及变量进窗口判断出窗口更新结果 我的答案 . 题目链接 找到字符串中所有的字母异位词 题目详情 题目解析 所谓的异位词,就是一个单词中的字母,打乱顺序,重新排列得到的单词 如:abc-&g…...
【Java EE初阶十九】网络原理(四)
4. 数据链路层 数据链路层也有很多种协议,其中一个比较常见常用的,就是“以太网协议”(通过网线/光纤, 来通信所使用的协议叫做以太网协议,以太网是横跨数据链路层 物理层); 4.1 以太网数据帧格式 帧头 载荷(IP 数据…...

12.23 校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、社招&校招 | 轻舟智航 社招 & 2024校招 社招&校招 | 轻舟智航 社招 & 2024校招 2、校招 | 成都精灵云科技2024校园招聘补录 校招 | 成都精灵云科技2024校园招聘补录 …...

FPGA转行ISP的探索之一:行业概览
ISP的行业位置 最近看到一个分析,说FPGA的从业者将来转向ISP(Image Signal Process图像信号处理)是个不错的选择,可以适应智能汽车、AI等领域。故而我查了一下ISP,对它大致有个概念。 传统的ISP对应的是相机公司&…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
