波奇学Linux:动静态库
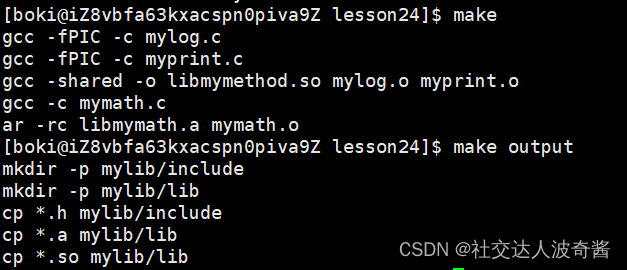
创建静态库
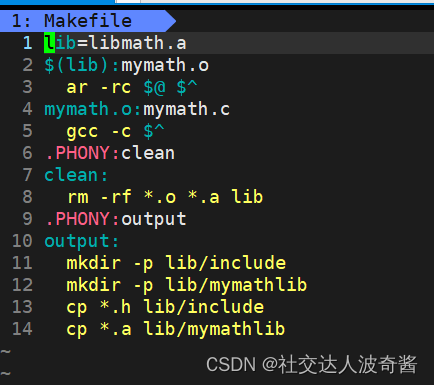
Makefile文件
mymath.c文件

mymath.h文件
编译main.c文件

gcc 编译时会把在系统目录中寻找头文件和库文件,文件不在系统目录中用参数
-I 头文件所在文件夹/ -L 库的地址文件夹 -l+除去lib和后缀。
拷贝文件到系统目录即可不用参数
库的安装类似于把头文件和库文件拷贝到系统文件中
库可以提供一个全局变量,如errno就是C语言提供的
如果系统默认动态链接,只提供静态链接,gcc只能提供静态链接。
动态库

动态库在程序运行时被加载到内存,所以产生库的方式和产生可执行程序的命令类似
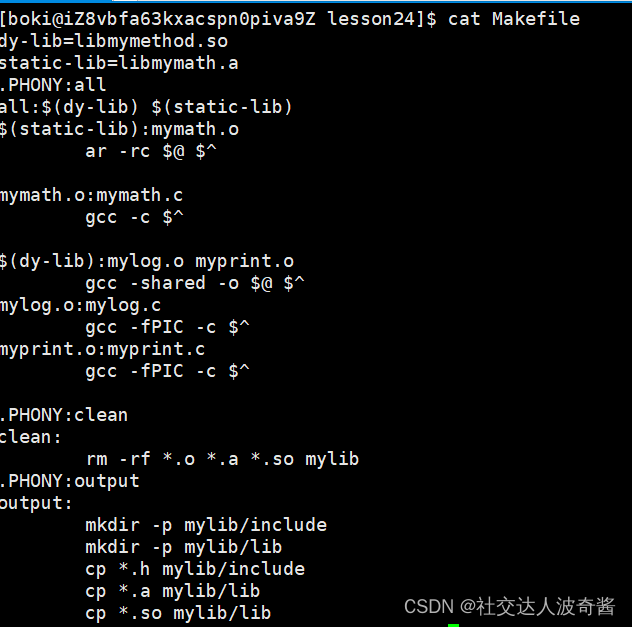

同时连接动静库

可执行程序链接动态库,必须让加载器和gcc编辑器同时知道位置,方法如下
方法一:把动态库拷贝到系统目录/lib64/usr/lib64
方法二:在系统目录创建软链接指向动态库

方法三:环境变量$LD_LIBRARY_PATH系统搜索动态库路径,将路径添加到这个变量里

方法四:/etc/ld.so.conf.d建立自己的路径动态库路径配置文件,然后重新ldconfig即可。
动静态库区别
静态库相当于把代码拷贝到可执行程序中,当可执行程序链接后,删掉静态库依然可以运行。
动态库相当于程序运行时跳出来运行动态库的代码,动态库删除后,程序不能运行。
动态库在系统中加载之后,会被所有的程序共享,在内存中只会被加载一份。
动态库加载
一份动态库加载到内存中通过页表映射加载到多个进程地址空间的共享区,正文代码运行到库的时候进入共享区。
执行的代码都是在进程地址空间进行执行。
系统在运行时,一定会存在多个动态库,通过os管理起来
动态库的数据会发生写时拷贝,如全局变量。
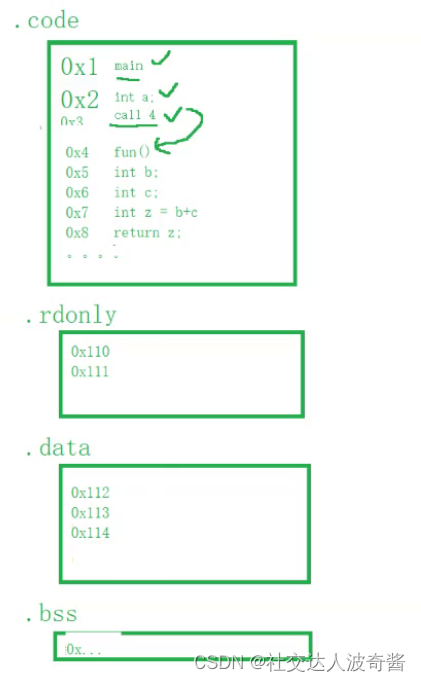
可执行程序编译完后没有加载到自己内存中有自己的地址。程序可以分区并有地址
平坦模式0~4GB,上面的地址并不是真实的物理地址,是逻辑地址
相关文章:

波奇学Linux:动静态库
创建静态库 Makefile文件 mymath.c文件 mymath.h文件 编译main.c文件 gcc 编译时会把在系统目录中寻找头文件和库文件,文件不在系统目录中用参数 -I 头文件所在文件夹/ -L 库的地址文件夹 -l除去lib和后缀。 拷贝文件到系统目录即可不用参数 库的安装类似于把头文件…...

1723. 完成所有工作的最短时间
文章目录 题意思路代码 题意 题目链接 K个工人,一共jobs个任务,问怎样分配任务,最短的最长工人完成任务完成时间。 思路 DFS剪枝(最大单个工人jobs时间超过ans时间;有限空闲工人拿任务)模拟退火dp 代码…...
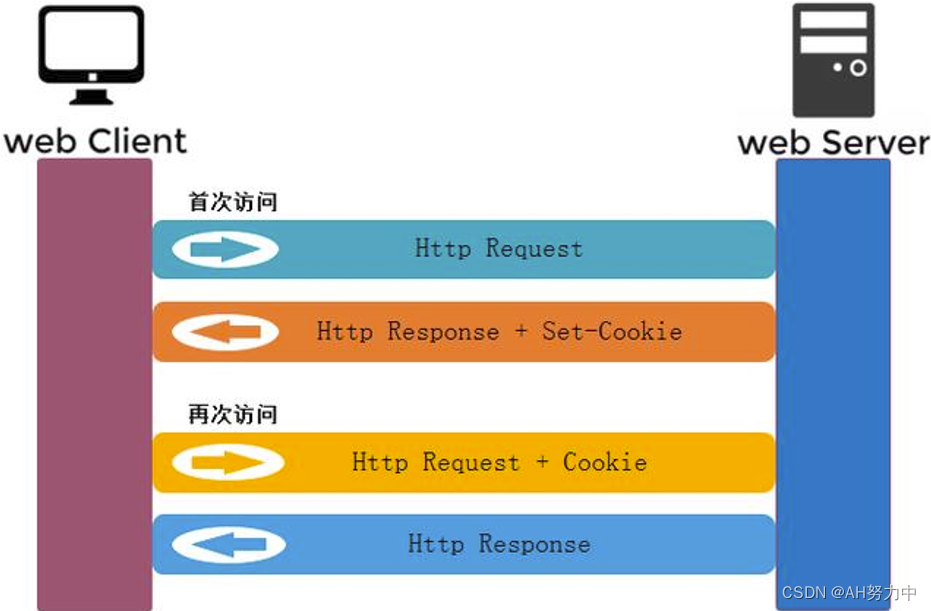
初始HTTP协议
一、http协议 1、http相关概念 互联网:是网络的网络,是所有类型网络的母集因特网:世界上最大的互联网网络。即因特网概念从属于互联网概念。习惯上,大家把连接在因特网上的计算机都成为主机。万维网:WWW(…...
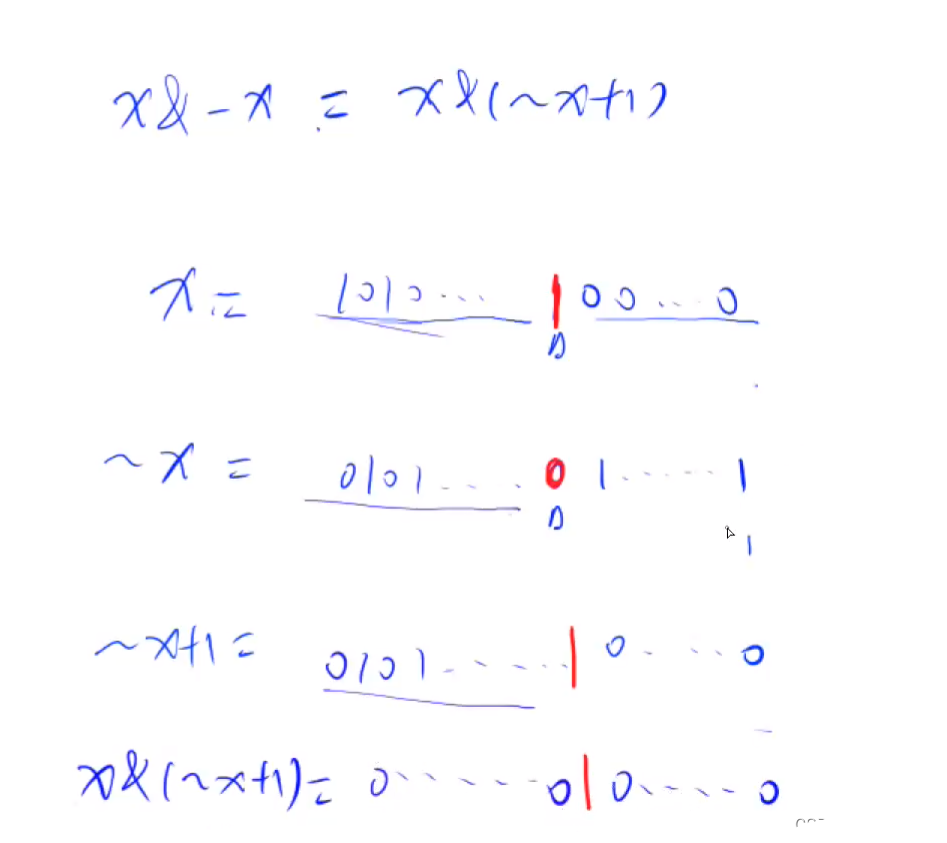
C++ 位运算常用操作 二进制中1的个数
给定一个长度为 n 的数列,请你求出数列中每个数的二进制表示中 1 的个数。 输入格式 第一行包含整数 n 。 第二行包含 n 个整数,表示整个数列。 输出格式 共一行,包含 n 个整数,其中的第 i 个数表示数列中的第 i 个数的二进制表…...

大数据领域的数据仓库
在大数据领域,数据仓库(Data Warehouse)是一个用于存储、管理和分析大量数据的集中式系统。它从多个异构数据源收集数据,对数据进行清洗、转换和整合,然后将其存储在一个集中的位置,以支持复杂的查询、报告…...
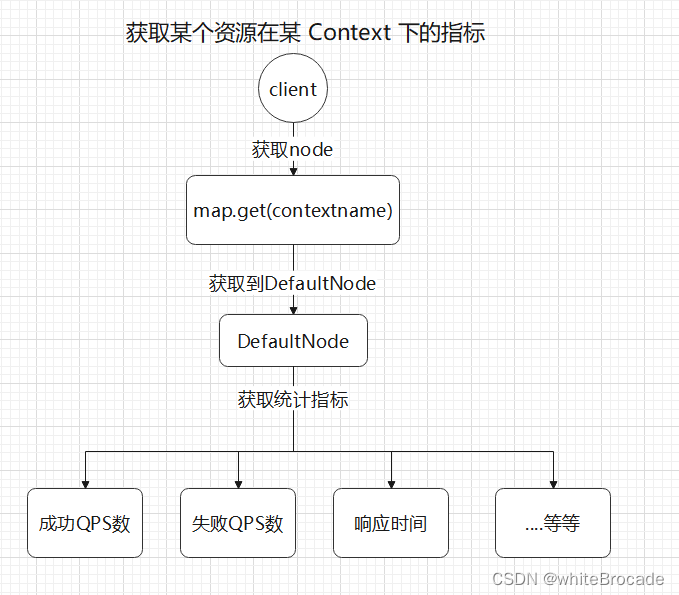
sentinel的资源数据指标是如何采集
资源数据采集 之前的NodeSelectorSlot和ClusterBuilderSlot已经完成了对资源调用树的构建, 现在则是要对资源进行收集, 核心点就是这些资源数据是如何统计 LogSlot 作用: 记录异常请求日志, 用于故障排查 public class LogSlot extends AbstractLinkedProcessorSlot<Def…...
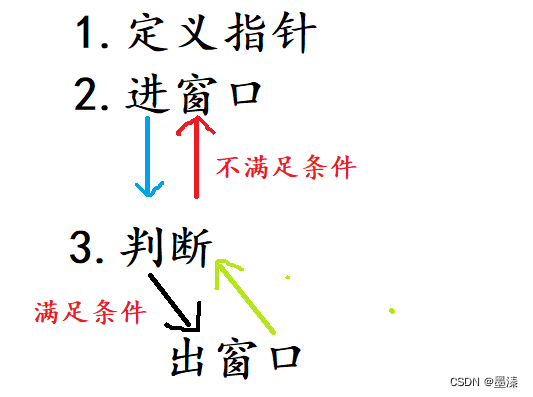
算法刷题:找到字符串中所有的字母异位词
找到字符串中所有的字母异位词 .题目链接题目详情题目解析算法原理滑动窗口流程图定义指针及变量进窗口判断出窗口更新结果 我的答案 . 题目链接 找到字符串中所有的字母异位词 题目详情 题目解析 所谓的异位词,就是一个单词中的字母,打乱顺序,重新排列得到的单词 如:abc-&g…...
【Java EE初阶十九】网络原理(四)
4. 数据链路层 数据链路层也有很多种协议,其中一个比较常见常用的,就是“以太网协议”(通过网线/光纤, 来通信所使用的协议叫做以太网协议,以太网是横跨数据链路层 物理层); 4.1 以太网数据帧格式 帧头 载荷(IP 数据…...

12.23 校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、社招&校招 | 轻舟智航 社招 & 2024校招 社招&校招 | 轻舟智航 社招 & 2024校招 2、校招 | 成都精灵云科技2024校园招聘补录 校招 | 成都精灵云科技2024校园招聘补录 …...

FPGA转行ISP的探索之一:行业概览
ISP的行业位置 最近看到一个分析,说FPGA的从业者将来转向ISP(Image Signal Process图像信号处理)是个不错的选择,可以适应智能汽车、AI等领域。故而我查了一下ISP,对它大致有个概念。 传统的ISP对应的是相机公司&…...

Linux系统之部署网页小游戏合集网站
Linux系统之部署网页游戏合集网站 一、项目介绍1.1 项目介绍1.2 自定义配置方法二、本次实践介绍2.1 环境规划2.2 本次实践介绍三、检查本地环境3.1 检查操作系统版本3.2 检查当前yum仓库四、安装httpd软件4.1 检查yum仓库4.2 安装httpd软件4.3 启动httpd服务4.4 查看httpd服务…...

【白嫖8k买的机构vip教程】python(2):python_re模块
python之re模块 一、正则表达式 re模块是python独有的匹配字符串的模块,该模块中提供的很多功能是基于正则表达式实现的,而正则表达式是对字符串进行模糊匹配,提取自己需要的字符串部分,他对所有的语言都通用。注意…...
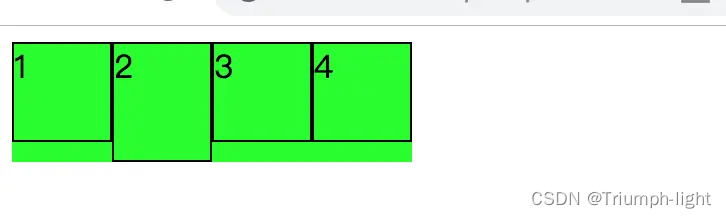
【CSS】display:flex和display: inline-flex区别
flex:将对象作为弹性伸缩盒显示 inline-flex:将对象作为内联块级弹性伸缩盒显示 DOM结构 <div class"main"><div></div><div></div><div></div><div></div></div>flex .main{…...

rpm安装gitlab
1.1 下载gitlab安装包 使用rpm包安装命令安装gitlab的rpm包,下载地址为https://packages.gitlab.com/gitlab/gitlab-ce社区版本; 推荐使用清华大学镜像:https://mirrors.tuna.tsinghua.edu.cn/gitlab-ce/yum/el7/gitlab安装包详见࿱…...
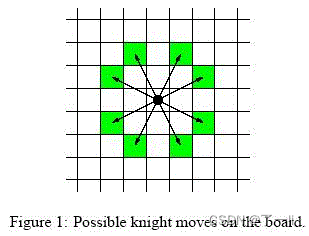
图论之dfs与bfs的练习
dfs--深度优选搜索 bfs--广度优先搜索 迷宫问题--dfs 问题: 给定一个n*m的二维迷宫数组其中S是起点,T是终点,*是墙壁(无法通过), .是道路 问从起点S出发沿着上下左右四个方向走,能否走到T点&a…...

Vue练习5:图片的引入
后续会补充 1.require引入 src -> asstes <template><img :src"url"> </template><script> export default {name: App,data(){return{url: require("./assets/logo.png"),}} } </script> 2.import引入 src…...

SpringBoot+Kafka
文章目录 一、依赖二、配置文件三、API1、生产者2、消费者 一、依赖 <!-- spring-kafka(与kafka的版本一致) --> <dependency><groupId>org.springframework.kafka</groupId><artifactId>spring-kafka</artifactId>…...

世界顶级名校计算机专业,都在用哪些书当教材?(文末送书)
目录 01《深入理解计算机系统》02《算法导论》03《计算机程序的构造和解释》04《数据库系统概念》05《计算机组成与设计:硬件/软件接口》06《离散数学及其应用》07《组合数学》08《斯坦福算法博弈论二十讲》参与规则 清华、北大、MIT、CMU、斯坦福的学霸们在新学期里…...
)
蓝桥杯刷题--python-8(2023 填空题)
0幸运数 - 蓝桥云课 (lanqiao.cn) res=0 for i in range (1,100000000):l_n=[]for j in str(i):l_n.append(int(j))if len(l_n) % 2 ==0:cur =len(l_n)>>1if sum(l_n[:cur])==sum(l_n[cur:]):res+=1 print(res) 0有奖问答 - 蓝桥云课 (lanqiao.cn) dfs def bfs(score, q…...

Eclipse - Reset Perspective
Eclipse - Reset Perspective 1. Window -> Perspective -> Reset Perspective2. Reset Perspective -> YesReferences 1. Window -> Perspective -> Reset Perspective 2. Reset Perspective -> Yes References [1] Yongqiang Cheng, https://yo…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

用 FFmpeg 实现 RTMP 推流直播
RTMP(Real-Time Messaging Protocol) 是直播行业中常用的传输协议。 一般来说,直播服务商会给你: ✅ 一个 RTMP 推流地址(你推视频上去) ✅ 一个 HLS 或 FLV 拉流地址(观众观看用)…...

[C++错误经验]case语句跳过变量初始化
标题:[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...
