3个密码学相关的问题
一、离散对数问题(Discrete Logarithm Problem, DLP)
问题描述:给定 有限阿贝尓群 G中的2个元素a和b,找出最小的正整数x满足:b = a ^^ x (或者证明这样的x不存在)。
二、阶数问题(Order Problem, OP)
问题描述:给定 有限阿贝尓群 G中的元素a,计算a的阶数(记号:| < a > |)。
三、根问题(Root Problem, RP)
问题描述:给定 有限阿贝尓群 G中的元素a,和整数x > 1,计算群元b,使得其满足 b ^^ x = a (或者证明群中不存在满足条件的元素)。
四、教科书描述

五、问题复杂度说明
易见,| < a > | = DLP (a, 1G), 即求阶问题和求单位元的离散对数问题等价,故有OP <= DLP。此外,若群阶已知,则群元的x次根可以高效求得,故有RP <= OP.
六、参考文献
《公钥加密和计算数论》(Public-Key Cryptography and Computational Number Theory),Edited by Kazimierz Alster, Jerzy Urbanowicz and Hugh C. Williams, de Gruyter, Berlin, Germany, 2001.
相关文章:

3个密码学相关的问题
一、离散对数问题(Discrete Logarithm Problem, DLP) 问题描述:给定 有限阿贝尓群 G中的2个元素a和b,找出最小的正整数x满足:b a ^^ x (或者证明这样的x不存在)。 二、阶数问题(O…...

5G网络eMBB、uRLLC、mMTC
ITU(国际电信联盟)于2015年9月正式定义了5G的三大应用场景:eMBB(增强型移动宽带)、uRLLC(低时延高可靠通信)、mMTC(海量物联网通信)。 eMBB是4G MBB(移动宽带…...
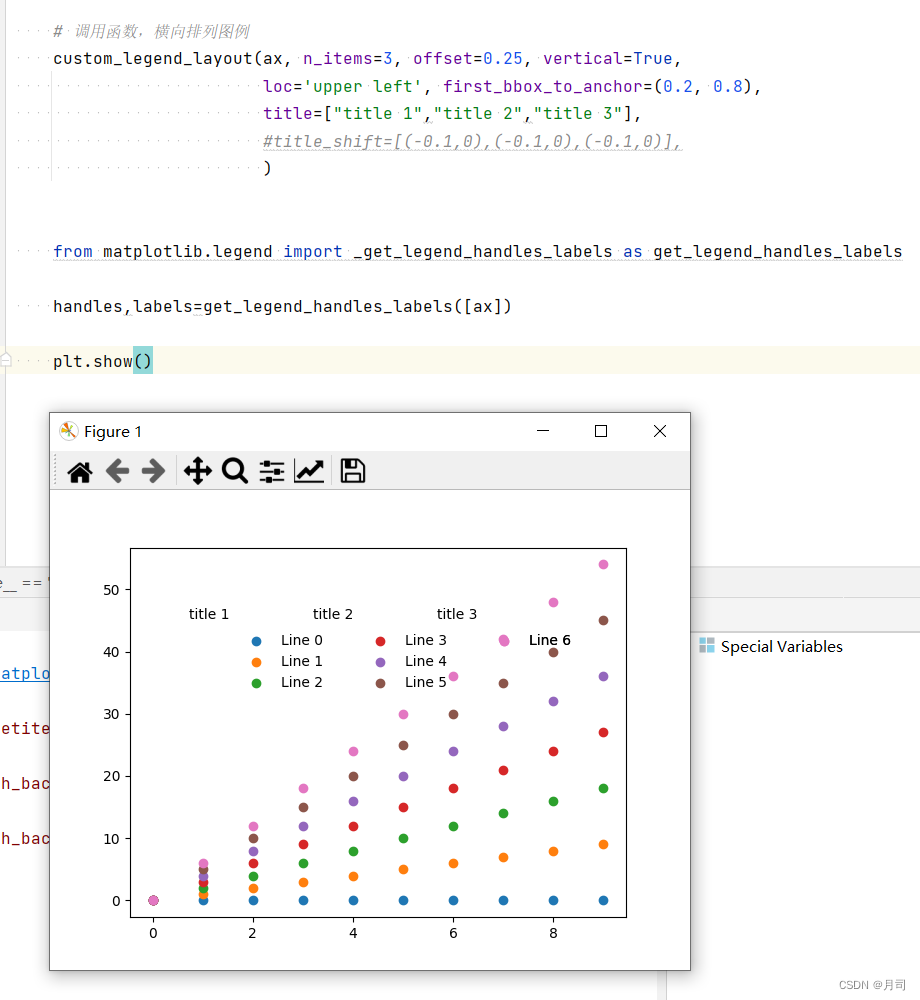
matplotlib图例使用案例1.1:在不同行或列的图例上添加title
我们将图例进行行显示或者列显示后,只能想继续赋予不同行或者列不同的title来进行分类。比较简单的方式,就是通过ax.annotate方法添加标签,这样方法复用率比较低,每次使用都要微调ax.annotate的显示位置。比较方便的方法是在案例1…...

nginx 日志改为json格式
nginx 日志改为json格式 场景描述效果变更旧样式新样式 场景描述 正常使用nginx时,使用默认的日志输出格式,对于后续日志接入其他第三方日志收集、清洗环节,因分隔符问题可能不是很友好。 xxxx - - [19/Feb/2024:11:16:48 0800] "GET …...
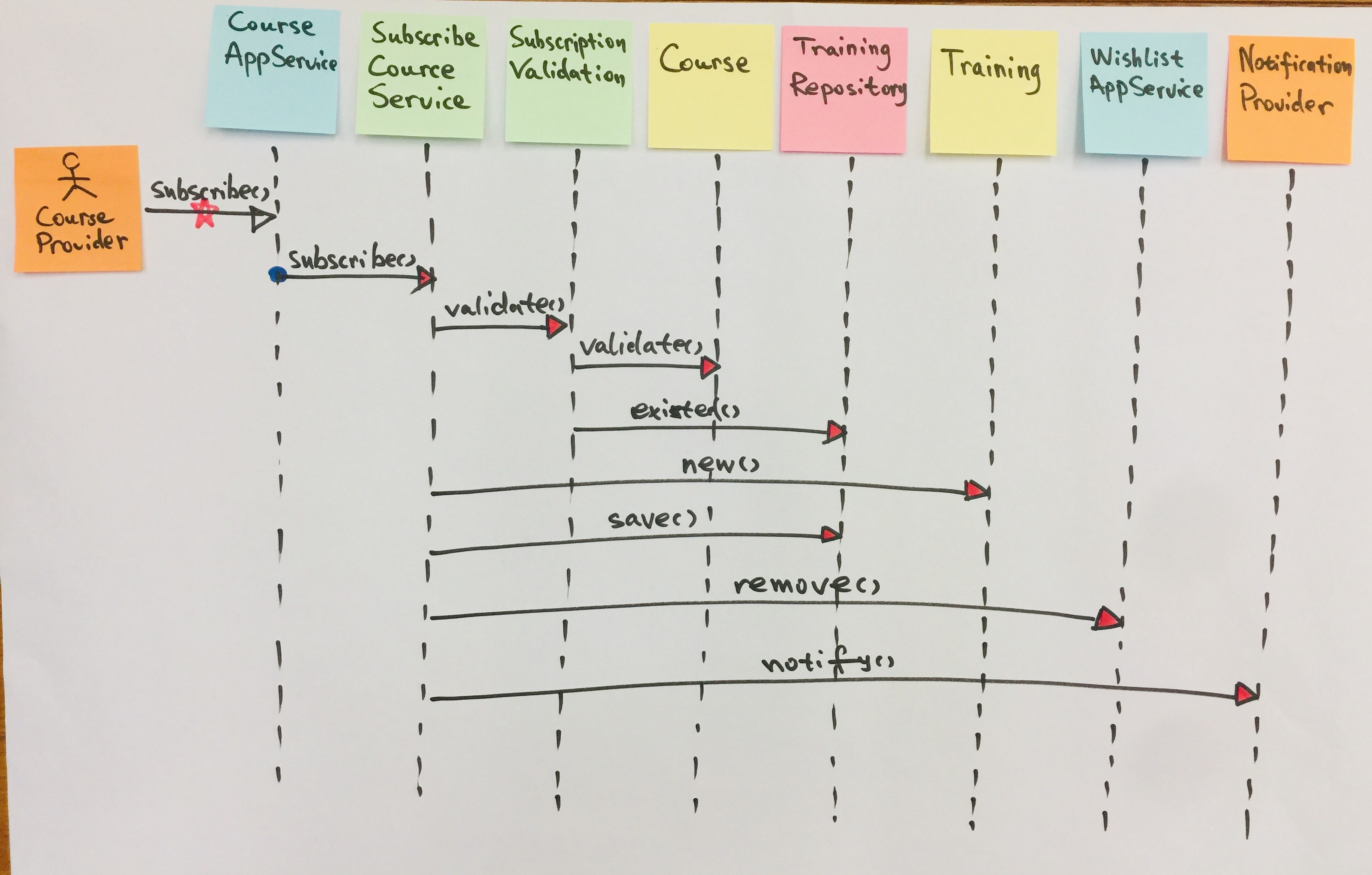
【DDD】学习笔记-应用服务
Eric Evans 为运用领域驱动设计的系统架构划定了层次,在领域层和展现层之间引入了应用层(Application Layer):“应用层要尽量简单,不包含业务规则或者知识,而只为下一层(指领域层)中…...
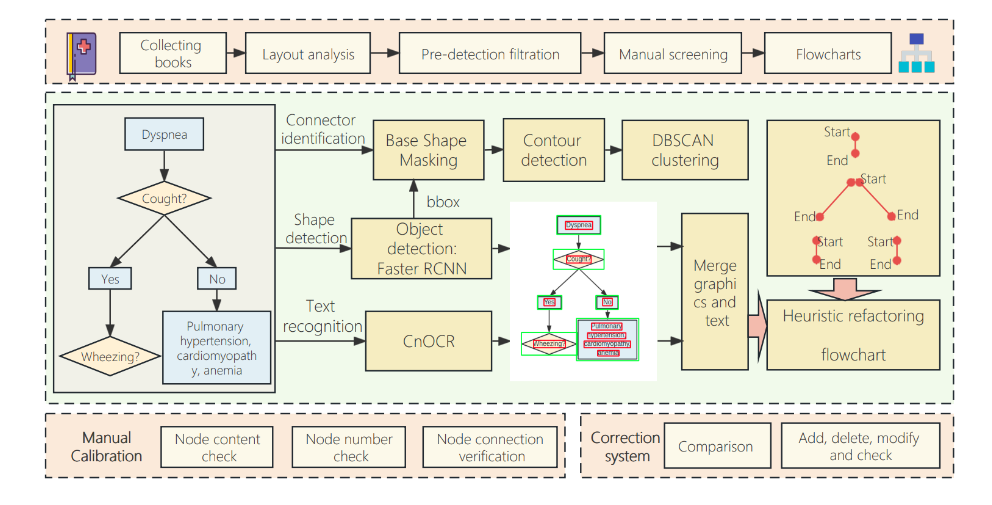
【医学大模型】MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用
MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用 提出背景对比传统医学大模型流程步骤临床指导树流程图识别临床决策支持系统 总结解决方案设计数据收集与处理系统实施临床决策支持 提出背景 论文:https://arxiv.org/p…...

YOLOV8改进系列指南
基于Ultralytics的YOLOV8改进项目.(69.9) 为了感谢各位对V8项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程 专栏改进汇总 二次创新系列 ultralytics/cfg/models/v8/yolov8-RevCol.yaml 使用(ICLR2023)Reversible Column Networks对yolov8主干进行重设计,里…...

FlinkSql一个简单的测试程序
FlinkSql一个简单的测试程序 以下是一个简单的 Flink SQL 示例,展示了如何使用 Flink Table API 和 Flink SQL 进行基本的数据流处理。 定义数据实体 CC : - CC 类表示数据流中的元素,包含两个字段: character (字符&a…...

二、ActiveMQ安装
ActiveMQ安装 一、相关环境二、安装Java8三、下载安装包四、启动五、其他命令六、开放端口七、后台管理 一、相关环境 环境:Centos7.9安装ActiveMQ版本:5.15.9JDK8 二、安装Java8 安装教程:https://qingsi.blog.csdn.net/article/details/…...

通俗易懂的L0范数和L1范数及其Python实现
定义 L0 范数(L0-Norm) L0 范数并不是真正意义上的一个范数,因为它不满足范数的三角不等式性质,但它在数学优化和信号处理等领域有着实际的应用。L0 范数指的是向量中非零元素的个数。它通常用来度量向量的稀疏性。数学上表示为…...

如何在30天内使用python制作一个卡牌游戏
如何在30天内使用python制作一个卡牌游戏 第1-5天:规划和设计第6-10天:搭建游戏框架第11-20天:核心游戏机制开发第21-25天:游戏界面和用户体验第26-30天:测试和发布附加建议游戏类型游戏规则设计界面设计技术选型第6-…...

VsCode指定插件安装目录
VsCode指定插件安装目录 VsCode安装的默认目录是在用户目录(%HomePath%)下的.vscode文件夹下的extensions目录下,随着安装插件越来越多会占用大量C盘空间。 指定VsCode的插件目录 Vscode安装目录: D:\Microsoft VS Code\Code.exeVscode插件安装目录&a…...
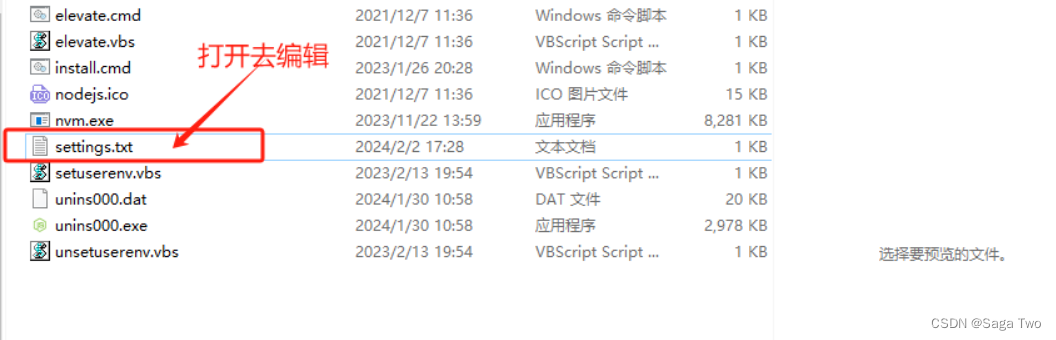
解决npm淘宝镜像到期问题
1 背景 由于node安装插件是从国外服务器下载,如果没有“特殊手法”,就可能会遇到下载速度慢、或其它异常问题。 所以如果npm的服务器在中国就好了,于是我们乐于分享的淘宝团队干了这事。你可以用此只读的淘宝服务代替官方版本,且…...

【JAVA】java泛型 详解
java泛型 详解 一、参数化类型(Parameterized Type):二. 泛型类(Generic Class):三. 泛型方法(Generic Method):四. 通配符类型(Wildcard Type)&a…...
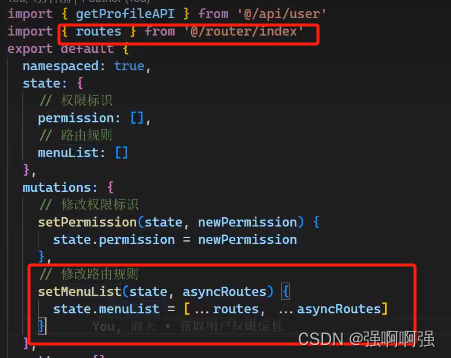
基于RBAC的权限管理的理论实现和权限管理的实现
权限管理的理论 首先需要两个页面支持,分别是角色管理和员工管理,其中角色管理对应的是角色和权限的配合,员工管理则是将登录的员工账号和员工所处的角色进行对应,即通过新增角色这个概念,让权限和员工并不直接关联&a…...

Atcoder ABC340 C - Divide and Divide
Divide and Divide(分而治之) 时间限制:2s 内存限制:1024MB 【原题地址】 所有图片源自Atcoder,题目译文源自脚本Atcoder Better! 点击此处跳转至原题 【问题描述】 【输入格式】 【输出格式】 【样例1】 【样例…...

趣学贝叶斯统计:概率密度分布(probability density function)
目录 1. 分布:PDF与PMFPDFPMF 2. 将概率密度函数应用于我们的问题用积分量化连续分布积分度量变化率:导数 3. R语言实践4. 小结 1. 分布:PDF与PMF PDF PDF定义在连续值上。在连续型随机变量的情况下,具体取某个数值的概率是0,因此PDF并不直…...

伦敦金行情分析需要学习吗?
对于伦敦金交易来说,目前大致分成两派,一派是实干派,认为做伦敦金交易重要的是实战,不需要学习太多东西,否则容易被理论知识所局限。另一派则是强调学习,没有理论知识,投资者很难做好伦敦金交易…...

Java实现停车场收费系统 JAVA+Vue+SpringBoot+MySQL
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 停车位模块2.2 车辆模块2.3 停车收费模块2.4 IC卡模块2.5 IC卡挂失模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 停车场表3.2.2 车辆表3.2.3 停车收费表3.2.4 IC 卡表3.2.5 IC 卡挂失表 四、系统实现五、核心代码…...
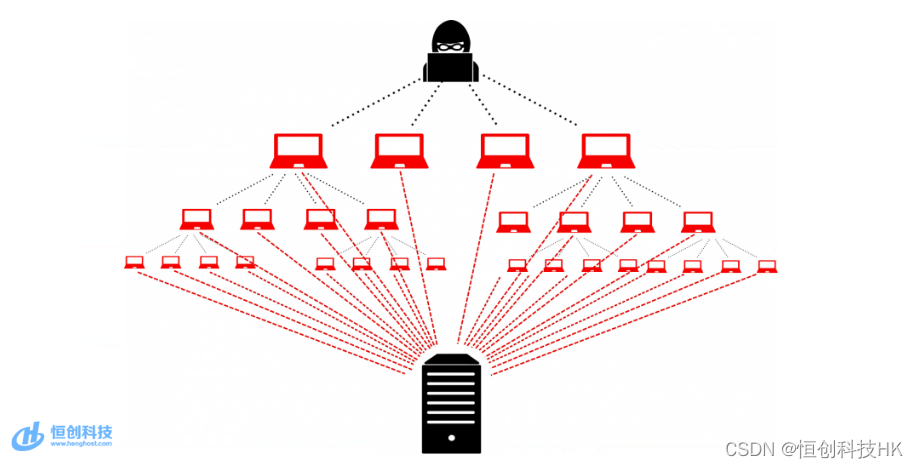
服务器遭受 DDoS 攻击的常见迹象有哪些?
服务器遭受 DDoS 攻击的现象很常见,并且有时不容易预防,有部分原因是它们的形式多种多样,而且黑客手段越来越隐蔽。如果您怀疑自己可能遭受 DDoS 攻击,可以寻找多种迹象。以下是 DDoS 攻击的5个常见迹象: 1.网络流量无…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...
