【动态规划专栏】专题一:斐波那契数列模型--------1.第N个泰波那契数
本专栏内容为:算法学习专栏,分为优选算法专栏,贪心算法专栏,动态规划专栏以及递归,搜索与回溯算法专栏四部分。 通过本专栏的深入学习,你可以了解并掌握算法。
💓博主csdn个人主页:小小unicorn
⏩专栏分类:动态规划专栏
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
专题一
- 题目来源
- 题目描述
- 题目解析
- 算法原理
- 1.状态表示
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值
- 代码实现
题目来源
本题来源为:
Leetcode1137. 第 N 个泰波那契数
题目描述
泰波那契序列 Tn 定义如下:
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2
给你整数 n,请返回第 n 个泰波那契数 Tn 的值。

题目解析
这里我们首先可以先将题目的公式变形一下:
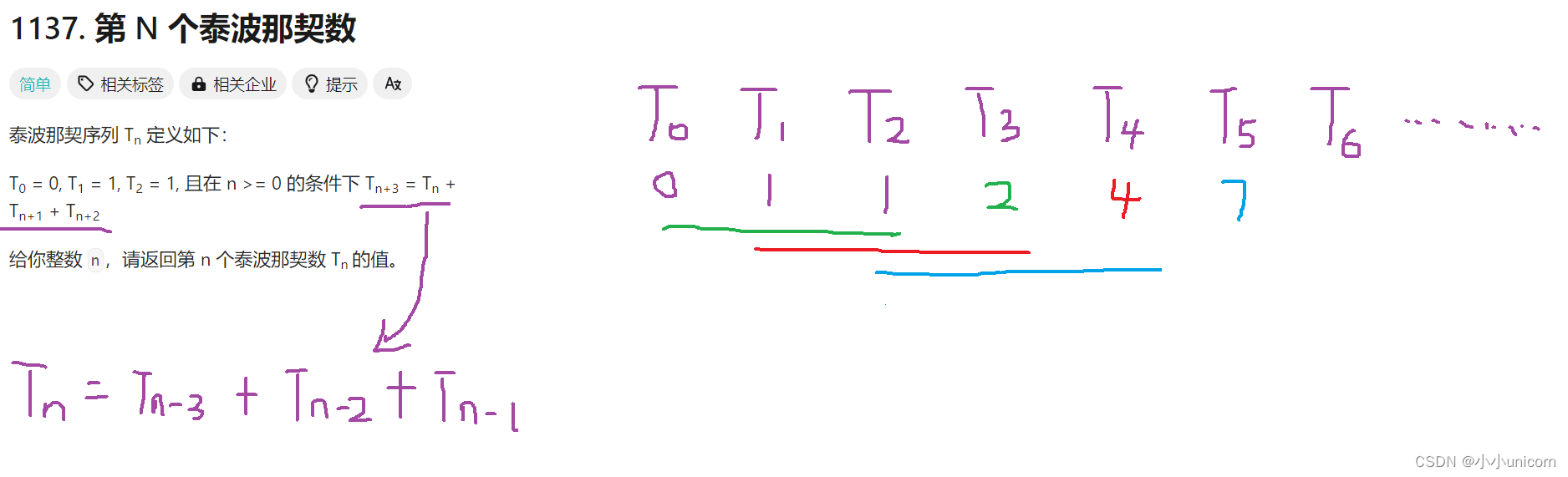
通过一个简单例子来理解此题目:
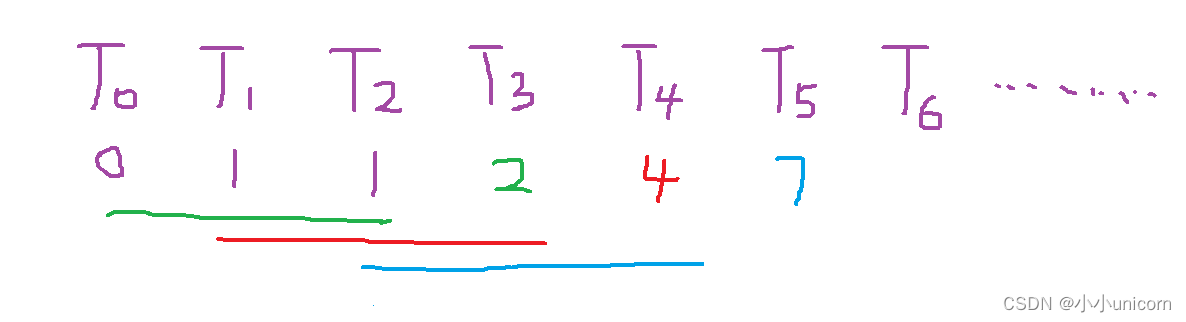
T0 T1 T2值题目中已经给出,而T4的值是T0 +T1+ T2的结果,而T5的值是T1 +T2+ T3的结果,依次内推…
算法原理
在讲解此题的算法原理之前,我们先了解一下动态规划:
[动态规划 dynamic programming」是一个重要的算法范式,它将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
可能此概念对于初学者来说很抽象,我们通过本题为例,给出动态规划的一般解决思路:
动态规划做题流程,一般会定义一个dp(动态规划的缩写)表(一位或者二维数组)
然后想办法把里面的值给填满,里面的某一个值可能就是我们的最终结果!
举个例子:
动态规划基本上分为五步:
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
其中状态转移方程由状态表示推出,而3.4.5步则为处理细节问题。
接下来将通过本题为例来讲解这五步如何处理:
1.状态表示
首先什么是状态表示呢?
简单点的说:状态表示就是dp表里面值的含义
那么具体怎么知道里面值所代表的含义呢?
基础有三种方式
1.1题目要求
1.2经验+题目要求(大多数)
1.3分析问题过程中,发现重复子问题(难点)
当然也不仅仅与此,后面也会再接触更多的方法!
那么根据本题目要求,
dp[i]表示:第i个泰波那契的值

2.状态转移方程
状态转移方程是什么?
通俗来说,就是推出一个式子,让dp[i]等于什么
根据本题要求,我们计算一个值时,需要知道它前面的三个值。
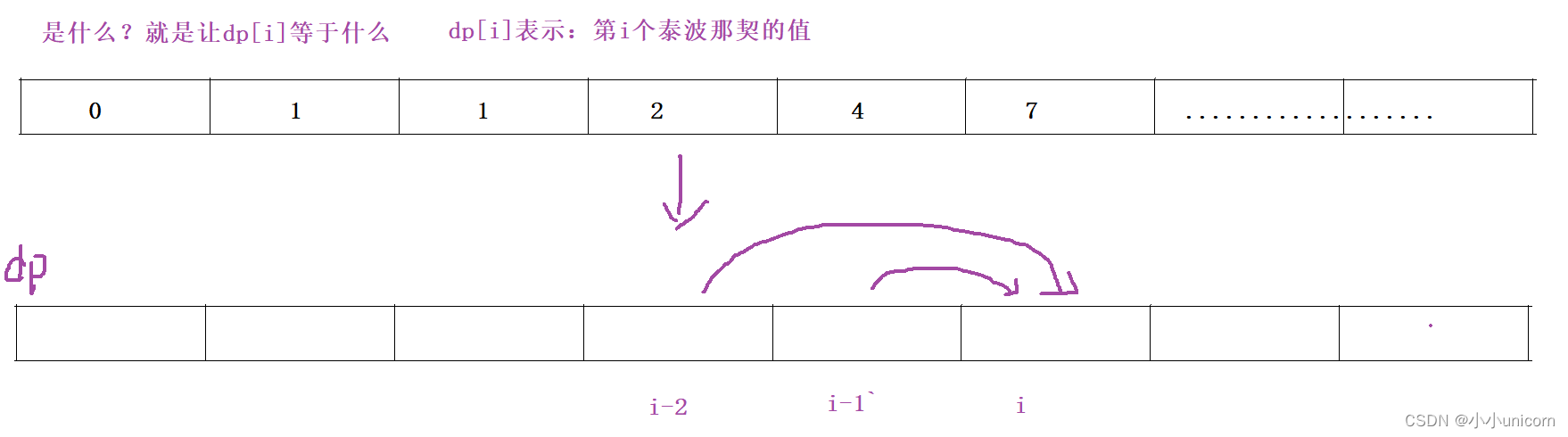
计算i位置的值(dp[i])时,需要知道i-1,i-2,i-3的值,那么i-1位置的值又怎么求呢?在回顾一下我们的状态表示,dp[i]表示:第i个泰波那契的值 那么i-1位置的值不就是dp[i-1],以此内推…
分析到这,我们的状态转移方程已经出来了:
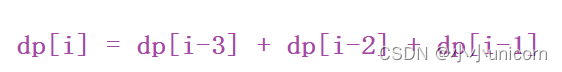
dp[i] = dp[i-3] + dp[i-2] + dp[i-1]
3.初始化
什么是初始化?
就是要保证填表的时候不越界

那么怎么填,其实就是根据状态转移方程,害怕越界访问,进行相关初始化 而本题的题目其实已经告诉我们了:
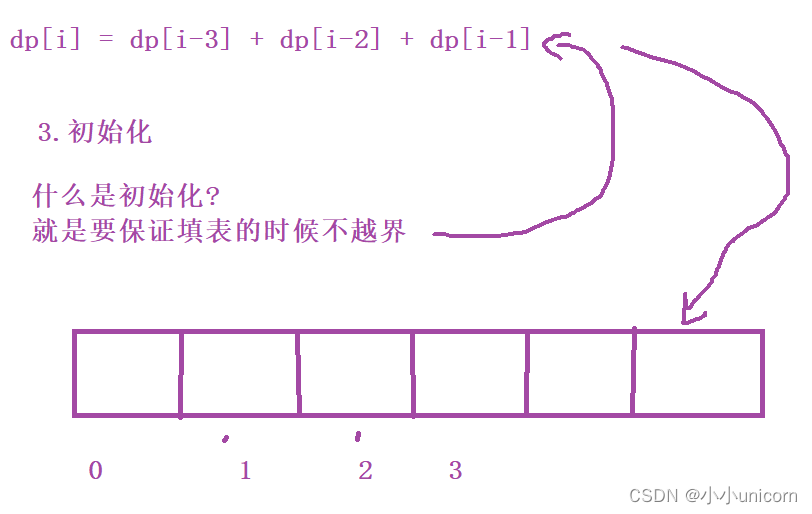
当i为0,1,2时就会产生越界访问,而本题的题目已经将这三个位置的值已经告诉我们了:
因此初始化为:
dp[0]=0
dp[1]=1
dp[2]=2
4.填表顺序
根据状态转移方程,我们计算dp[i]位置的值需要i-1与i-2位置的值,因此我们的填表顺序为:从左往右
5.返回值
根据题目要求返回第 n 个泰波那契数 Tn 的值。
而我们的状态表示 :dp[i]表示:第i个泰波那契的值
因此返回dp[n]
代码实现
动态规划的代码基本就是固定的四步:
1.创建dp表
2.初始化
3.填表
4.返回值
class Solution
{
public:int tribonacci(int n) {// 1.创建dp表// 2.初始化// 3.填表// 4.返回值//处理一下边界情况:if(n==0)return 0;if(n==1||n==2)return 1;//创建dp表vector<int> dp(n+1);//初始化dp[0]=0;dp[1]=dp[2]=1;//填表:for(int i=3;i<=n;i++){dp[i] = dp[i-1]+ dp[i-2] +dp[i-3];}//返回值:return dp[n];}
};
注意n的取值范围:
0 <= n <= 37
因此要处理一下边界情况:
//处理一下边界情况if(n==0)return 0;if(n==1||n==2)return 1;
时间复杂度:O(N)
空间复杂度:O(N)
相关文章:

【动态规划专栏】专题一:斐波那契数列模型--------1.第N个泰波那契数
本专栏内容为:算法学习专栏,分为优选算法专栏,贪心算法专栏,动态规划专栏以及递归,搜索与回溯算法专栏四部分。 通过本专栏的深入学习,你可以了解并掌握算法。 💓博主csdn个人主页:小…...

自养号测评低成本高效率推广,安全可控
测评的作用在于让用户更真实、清晰、快捷地了解产品以及产品的使用方法和体验。通过买家对产品的测评,也可以帮助厂商和卖家优化产品缺陷,提高用户的使用体验。这进而帮助他们获得更好的销量,并更深入地了解市场需求。因此,测评在…...

ubuntu22.04@laptop OpenCV Get Started: 015_deep_learning_with_opencv_dnn_module
ubuntu22.04laptop OpenCV Get Started: 015_deep_learning_with_opencv_dnn_module 1. 源由2. 应用Demo2.1 C应用Demo2.2 Python应用Demo 3. 使用 OpenCV DNN 模块进行图像分类3.1 导入模块并加载类名文本文件3.2 从磁盘加载预训练 DenseNet121 模型3.3 读取图像并准备为模型输…...
【elk查日志 elastic(kibana)】
文章目录 概要具体的使用方式一:查找接口调用历史二:查找自己的打印日志三:查找错误日志 概要 每次查日志,我都需要别人帮我,时间长了总觉得不好意思,所以这次下定决心好好的梳理一下,怎么查日…...
RapidMiner数据挖掘2 —— 初识RapidMiner
本节由一系列练习与问题组成,这些练习与问题有助于理解多个基本概念。它侧重于各种特定步骤,以进行直接的探索性数据分析。因此,其主要目标是测试一些检查初步数据特征的方法。大多数练习都是关于图表技术,通常用于数据挖掘。 为此…...

基于STM32的光照检测系统设计
基于STM32的光照检测系统设计 摘要: 随着物联网和智能家居的快速发展,光照检测系统在智能环境控制中扮演着越来越重要的角色。本文设计了一种基于STM32的光照检测系统,该系统能够实时检测环境光强度,并根据光强度调节照明设备,实现智能照明控制。本文首先介绍了系统的总体…...
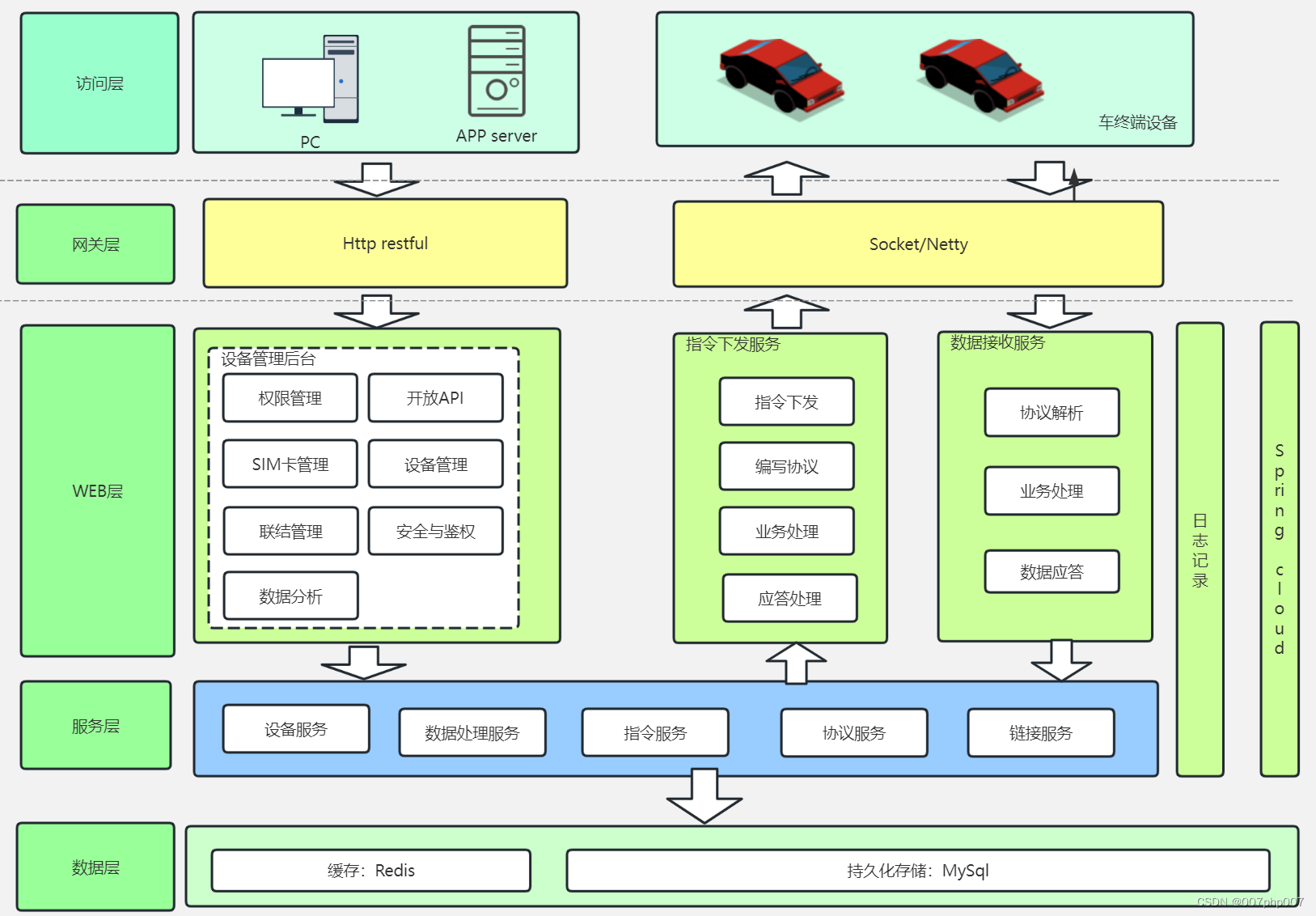
车辆管理系统设计与实践
车辆管理系统是针对车辆信息、行驶记录、维护保养等进行全面管理的系统。本文将介绍车辆管理系统的设计原则、技术架构以及实践经验,帮助读者了解如何构建一个高效、稳定的车辆管理系统。 1. 系统设计原则 在设计车辆管理系统时,需要遵循以下设计原则&…...
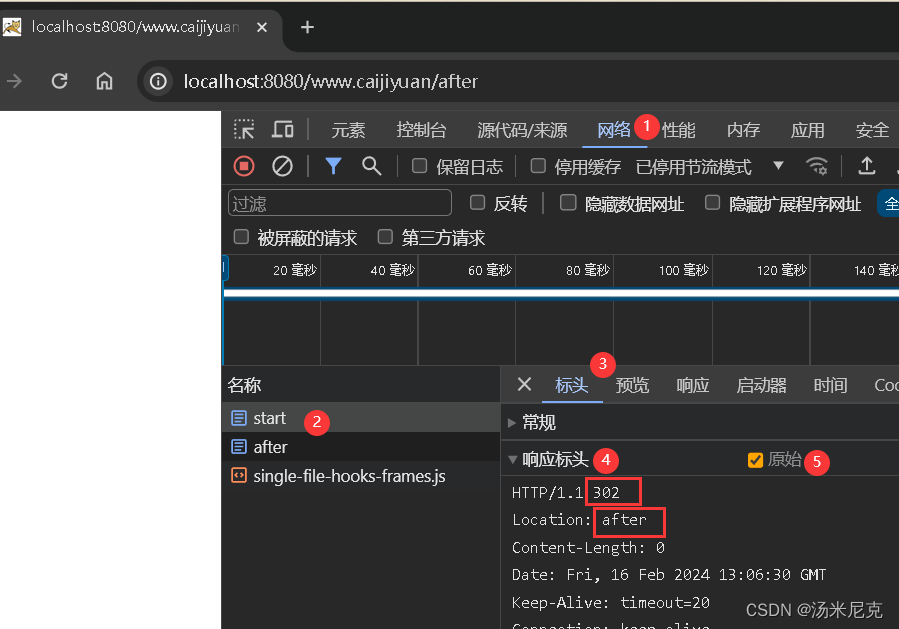
板块一 Servlet编程:第四节 HttpServletResponse对象全解与重定向 来自【汤米尼克的JAVAEE全套教程专栏】
板块一 Servlet编程:第四节 HttpServletResponse对象全解与重定向 一、什么是HttpServletResponse二、响应数据的常用方法三、响应乱码问题字符流乱码字节流乱码 四、重定向:sendRedirect请求转发和重定向的区别 在上一节中,我们系统的学习了…...

漫谈:C/C++ char 和 unsigned char 的用途
C/C的字符默认是有符号的,这一点非常的不爽,因为很少有人用单字节表达有符号数,毕竟,ASCII码是无符号的,对字符的绝大多数处理都是基于无符号的。 这一点在其它编程语言上就好很多,基本上都提供了byte这种类…...

安全保护制度
安全保护制度 第九条 计算机信息系统实行安全等级保护。安全等级的划分标准和安全等级保护的具体办法,由公安部会同有关部门制定。 第十条 计算机机房应当符合国家标准和国家有关规定。 在计算机机房附近施工,不得危害计算机信息系统的安全。 第十一条 进行国际联网的计算…...

沁恒CH32V30X学习笔记07---多功能按键框架使用
多功能按键框架使用 参考开源框架: GitHub - 0x1abin/MultiButton: Button driver for embedded system 框架使用说明: ch32gpio基本驱动 https://blog.csdn.net/u010261063/article/details/136157718 MultiButton 简介 MultiButton 是一个小巧简单易用的事件驱动型按…...

如何看显卡是几G?
created: 2024-02-20T09:22:13 (UTC 08:00) tags: [] source: https://www.sysgeek.cn/windows-check-gpu-model/ author: 海猴子 6 种简单方法:如何在 Windows 中轻松查看显卡型号 - 系统极客 Excerpt 不确定你的显卡型号?使用这 6 个简单有效的方法&a…...
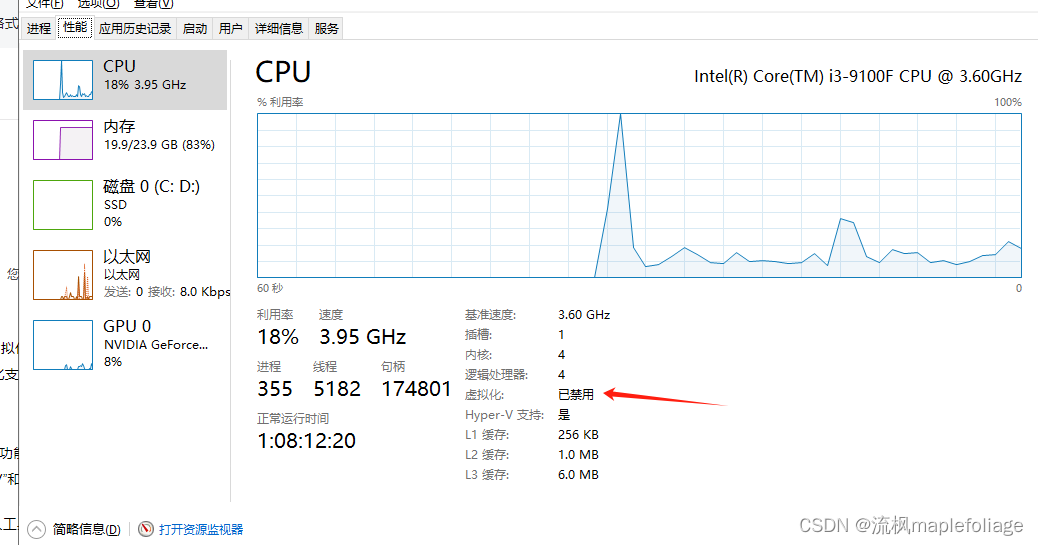
虚拟机--pc端和macOS端互通
windows开启虚拟化 要在Windows系统中开启虚拟化,您可以按照以下步骤操作: 准备工作: 确保您的计算机CPU支持虚拟化技术。在BIOS中开启相应的虚拟化支持。 开启虚拟化: 打开控制面板,点击程序或功能项&am…...

(14)Hive调优——合并小文件
目录 一、小文件产生的原因 二、小文件的危害 三、小文件的解决方案 3.1 小文件的预防 3.1.1 减少Map数量 3.1.2 减少Reduce的数量 3.2 已存在的小文件合并 3.2.1 方式一:insert overwrite (推荐) 3.2.2 方式二:concatenate 3.2.3 方式三ÿ…...

Linux 驱动开发基础知识——LED 模板驱动程序的改造:设备树(十一)
个人名片: 🦁作者简介:学生 🐯个人主页:妄北y 🐧个人QQ:2061314755 🐻个人邮箱:2061314755qq.com 🦉个人WeChat:Vir2021GKBS 🐼本文由…...

学习文档:QT QTreeWidget及其代理
学习文档:QT QTreeWidget及其代理 1. QT QTreeWidget简介 QT QTreeWidget是QT框架中的一个重要组件,用于显示树形数据结构。它提供了一种方便的方式来展示并操作带有层次关系的数据。QTreeWidget可以显示包含多个列的树形视图,每个项目可以…...

代码随想录算法训练营——总结篇
不知不觉跟完了代码训练营为期两个月的训练,现在来做个总结吧~ 记得去年12月上旬的时候,我每天都非常浮躁。一方面,经历了三个多月的秋招,我的日常学习和实验室进展被完全打乱,导致状态很差;另一方面&#…...
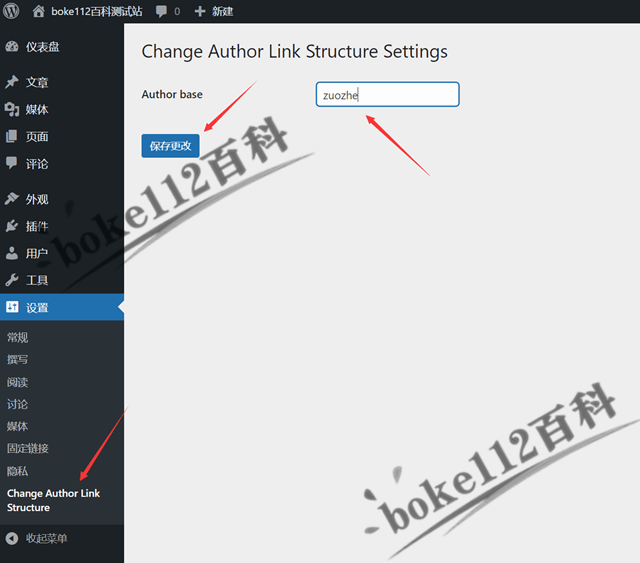
更改WordPress作者存档链接author和用户名插件Change Author Link Structure
WordPress作者存档链接默认情况为/author/Administrator(用户名),为了防止用户名泄露,我们可以将其改为/author/1(用户ID),具体操作可参考『如何将WordPress作者存档链接中的用户名改为昵称或ID…...
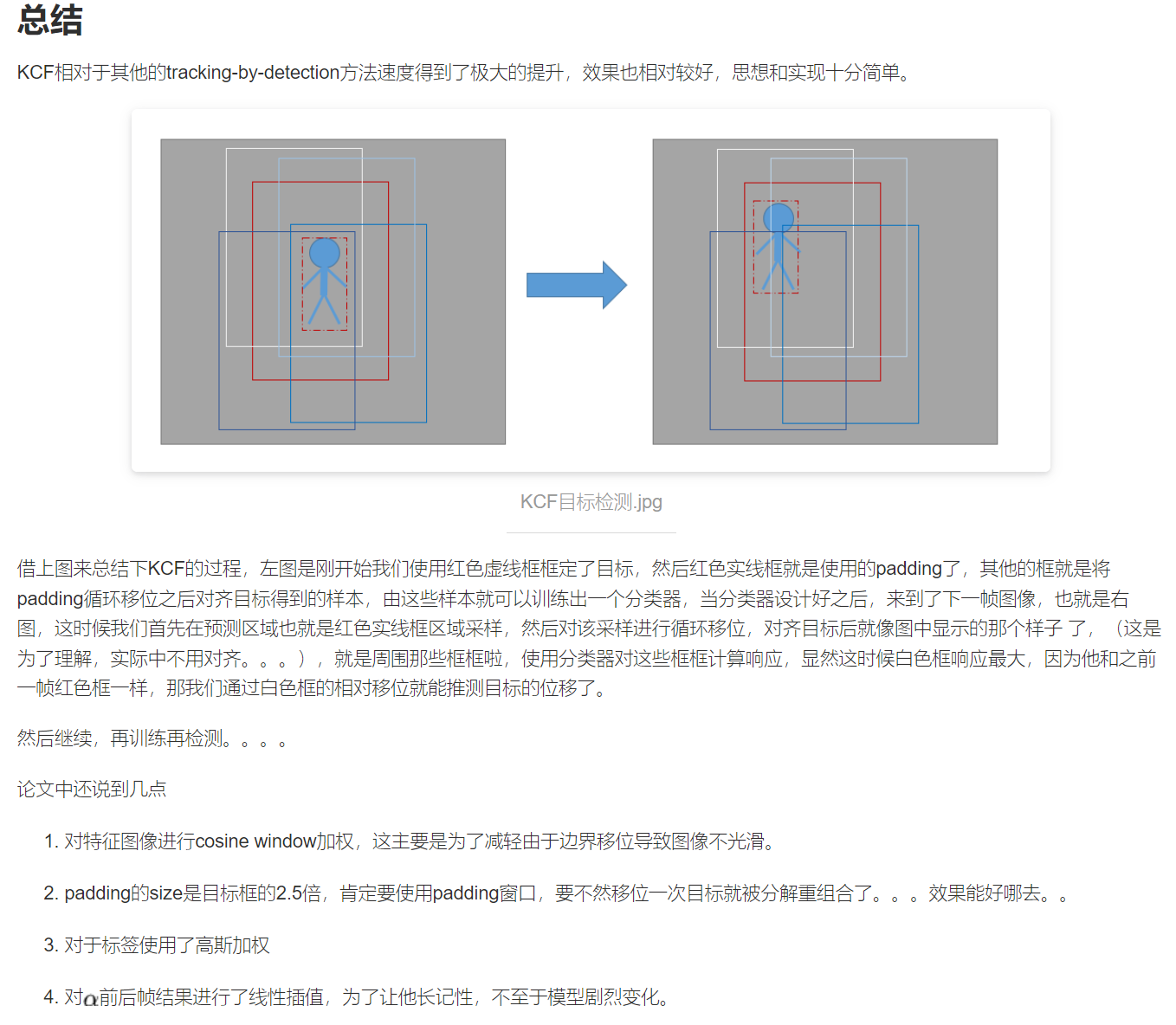
Kernelized Correlation Filters KCF算法原理详解(阅读笔记)(待补充)
KCF 目录 KCF预备知识1. 岭回归2. 循环移位和循环矩阵3. 傅里叶对角化4. 方向梯度直方图(HOG) 正文1. 线性回归1.1. 岭回归1.2. 基于循环矩阵获取正负样本1.3. 基于傅里叶对角化的求解 2. 使用非线性回归对模型进行训练2.1. 应用kernel-trick的非线性模型…...
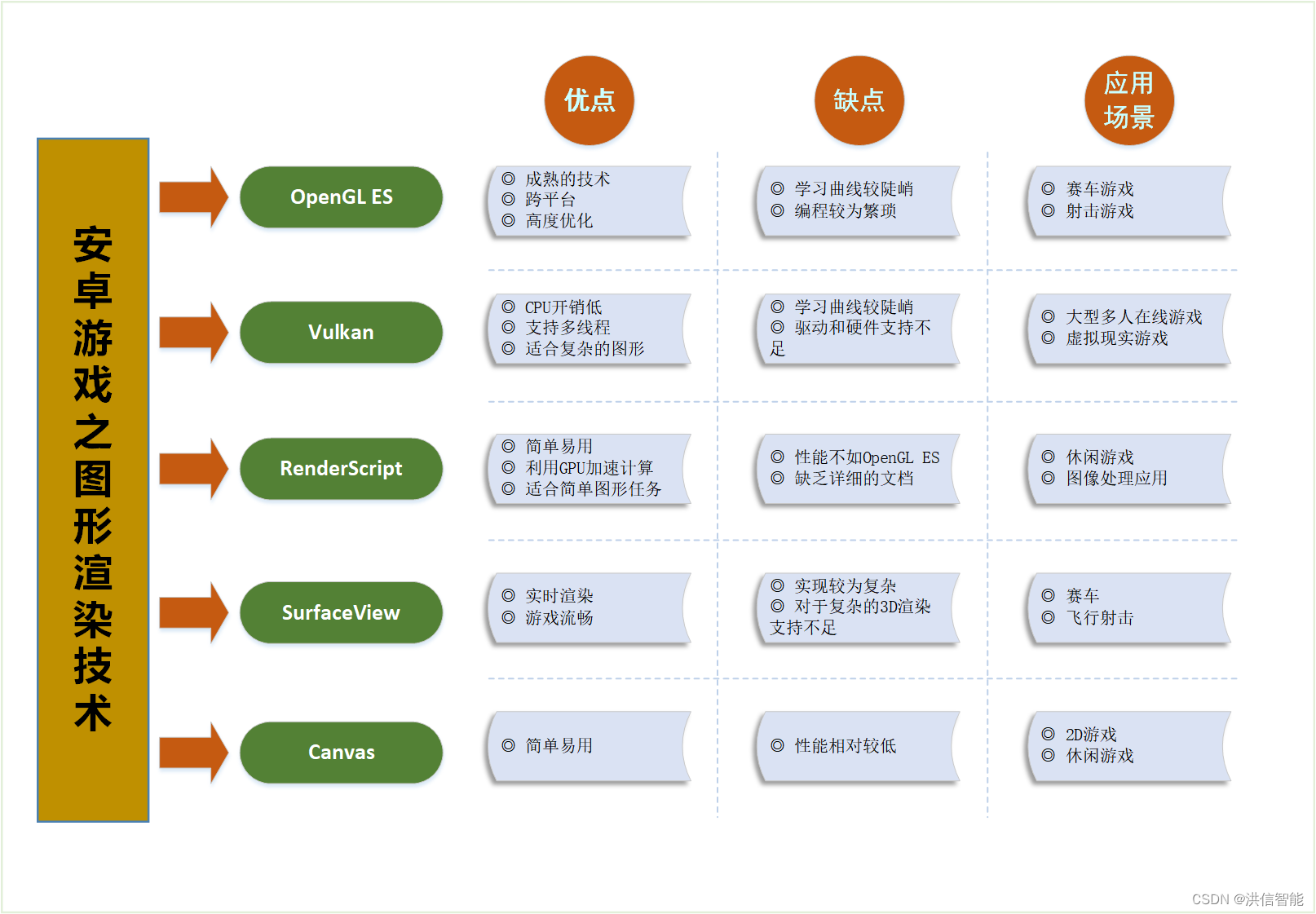
安卓游戏开发之图形渲染技术优劣分析
一、引言 随着移动设备的普及和性能的提升,安卓游戏开发已经成为一个热门领域。在安卓游戏开发中,图形渲染技术是关键的一环。本文将对安卓游戏开发中常用的图形渲染技术进行分析,比较它们的优劣,并探讨它们在不同应用场景下的适用…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
