算法沉淀——递归(leetcode真题剖析)

算法沉淀——递归
- 01.汉诺塔问题
- 02.合并两个有序链表
- 03.反转链表
- 04.两两交换链表中的节点
- 05.Pow(x, n)
递归是一种通过调用自身的方式来解决问题的算法。在递归算法中,问题被分解为更小的相似子问题,然后通过对这些子问题的解进行组合来解决原始问题。递归算法通常包含两个主要部分:
- 基本情况(Base Case): 定义问题的最小规模,直接解答而不再进行递归。基本情况是递归算法的出口,防止算法陷入无限递归。
- 递归步骤: 在问题规模较大时,将问题划分为相似但规模较小的子问题,并通过递归调用解决这些子问题。递归调用自身是递归算法的核心。
递归算法在解决许多问题上非常强大,尤其是对于那些可以通过分解为子问题并且存在重叠子问题的情况。递归通常使算法更加简洁、清晰,但需要谨慎处理基本情况,以避免无限递归。
经典的递归问题包括汉诺塔问题、阶乘计算、斐波那契数列等。递归也在许多算法和数据结构中发挥着重要的作用,例如树的遍历、图的深度优先搜索等。
如何理解递归?
1.递归展开的细节图
2.二叉树中的题目
3.宏观看待递归的过程
1.不要在意递归的细节展开图
2.把递归的函数当成一个黑盒
3.相信这个黑盒一定能完成这个任务
如何写好递归?
1.先找到相同的子问题!!!->函数头的设计
2.只关心某一个子问题是如何解决的 ->函数体的书写
3.注意一下递归函数的出口即可
01.汉诺塔问题
题目链接:https://leetcode.cn/problems/hanota-lcci/
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = []输出:C = [2, 1, 0]
示例2:
输入:A = [1, 0], B = [], C = []输出:C = [1, 0]
提示:
- A中盘子的数目不大于14个。
思路
对于这类问题我们可以使用数学中的归结思想,先画图分析由1到n的情况,我们可以总结出下面这三个步骤
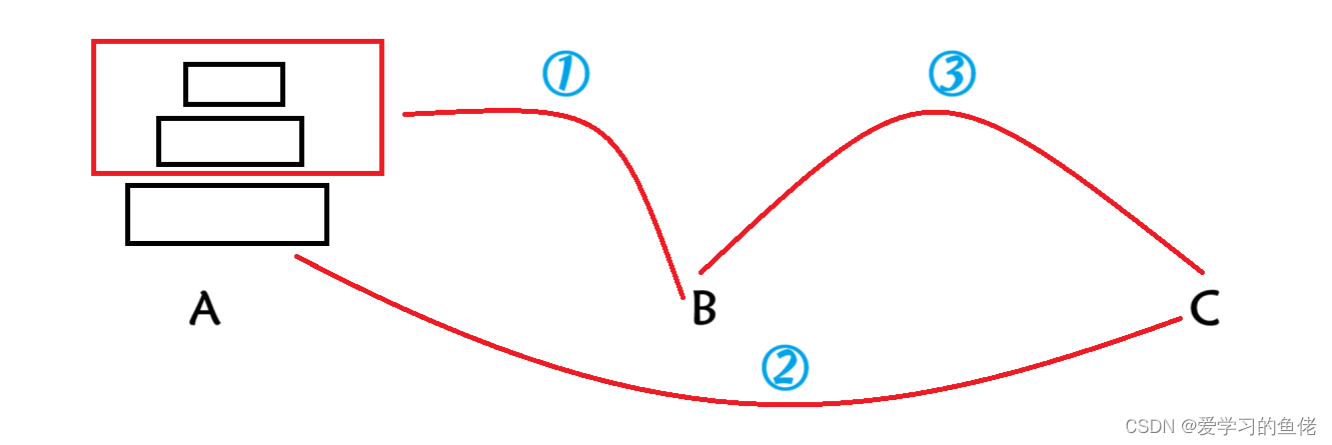
代码
class Solution {void dfs(vector<int>& A, vector<int>& B, vector<int>& C,int n){if(n==1){C.push_back(A.back());A.pop_back();return;}dfs(A,C,B,n-1);C.push_back(A.back());A.pop_back();dfs(B,A,C,n-1);}
public:void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}
};
- 定义一个私有的递归函数
dfs,该函数将 A 柱上的 n 个盘子通过 B 柱移动到 C 柱。参数A、B和C分别表示三个柱子的盘子状态,n表示要移动的盘子数量。 - 在递归函数中,当只有一个盘子时,直接将 A 柱的盘子移到 C 柱上,然后返回。
- 在递归函数中,先将 A 柱上的 n-1 个盘子通过 C 柱移动到 B 柱上,然后将 A 柱上的最后一个盘子移动到 C 柱上,最后将 B 柱上的 n-1 个盘子通过 A 柱移动到 C 柱上。
- 在公有函数
hanota中,调用递归函数dfs,传入 A、B、C 三个柱子的状态和盘子数量。
02.合并两个有序链表
题目链接:https://leetcode.cn/problems/merge-two-sorted-lists/
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
- 两个链表的节点数目范围是
[0, 50] -100 <= Node.val <= 100l1和l2均按 非递减顺序 排列
思路
这里我们如果划分为子问题,每次就拿出最小的那个节点当做头节点,拼接剩下的当前节点尾部的节点和另一个链表的头节点相比较的更小的点,最后谁被拼接完了,就直接拼接另一条链表剩下的,这样不难看出,每次的步骤都是重复的,于是我们可以使用递归的思想来解决这道问题。
代码
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(!list1) return list2;if(!list2) return list1;if(list1->val<=list2->val){list1->next=mergeTwoLists(list1->next,list2);return list1;}else{list2->next=mergeTwoLists(list2->next,list1);return list2;}}
};
- 如果
list1为空,说明第一个链表为空,直接返回list2。 - 如果
list2为空,说明第二个链表为空,直接返回list1。 - 接下来比较
list1和list2的头节点的值,选择较小的节点作为新链表的头节点。 - 如果
list1的头节点值小于等于list2的头节点值,将list1的下一个节点与list2合并,并返回list1作为新链表的头节点。 - 如果
list2的头节点值小于list1的头节点值,将list2的下一个节点与list1合并,并返回list2作为新链表的头节点。
03.反转链表
题目链接:https://leetcode.cn/problems/reverse-linked-list/
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目范围是
[0, 5000] -5000 <= Node.val <= 5000
**进阶:**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
思路
若我们直接遍历到最后的节点再逐个向前改变指向,在每次接入前一个节点时,将它的next指向空,最终返回头节点即可。
- 递归函数的含义:交给你⼀个链表的头指针,你帮我逆序之后,返回逆序后的头结点;
- 函数体:先把当前结点之后的链表逆序,逆序完之后,把当前结点添加到逆序后的链表后面即可;
- 递归出口:当前结点为空或者当前只有⼀个结点的时候,不用逆序,直接返回
代码
class Solution {
public:ListNode* reverseList(ListNode* head) {if(!head||!head->next) return head;ListNode* newhead = reverseList(head->next);head->next->next=head;head->next=nullptr;return newhead;}
};
04.两两交换链表中的节点
题目链接:https://leetcode.cn/problems/swap-nodes-in-pairs/
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
提示:
- 链表中节点的数目在范围
[0, 100]内 0 <= Node.val <= 100
思路
我们将问题划分为子问题,先交换当前节点的下两个节点,将当前节点的下一个节点作为新的头节点,将当前节点的下一个节点指向递归操作的结果,返回新的头节点。
代码
class Solution {
public:ListNode* swapPairs(ListNode* head) {// 如果链表为空或者只有一个节点,无需交换,直接返回原链表头指针if (!head || !head->next)return head;// 递归调用,交换当前节点的下两个节点ListNode* tmp = swapPairs(head->next->next);// 将当前节点的下一个节点作为新的头节点ListNode* ret = head->next;// 将当前节点的下一个节点指向当前节点,实现交换head->next->next = head;// 将当前节点的下一个节点指向递归操作的结果head->next = tmp;// 返回新的头节点return ret;}
};
if (!head || !head->next):检查链表是否为空或者只有一个节点。如果是,直接返回原链表头指针,因为不需要进行交换。ListNode* tmp = swapPairs(head->next->next);:递归调用swapPairs函数,传入当前节点的下两个节点。这样就会从链表的末尾开始,每次交换两个相邻的节点,然后返回新的头节点。ListNode* ret = head->next;:将当前节点的下一个节点作为新的头节点,因为在交换过程中,它会变成新的头节点。head->next->next = head;:将当前节点的下一个节点指向当前节点,实现交换操作。head->next = tmp;:将当前节点的下一个节点指向递归操作的结果,即当前节点的下两个节点交换后的头节点。return ret;:返回新的头节点,作为上层递归调用的结果。
05.Pow(x, n)
题目链接:https://leetcode.cn/problems/powx-n/
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,xn )。
示例 1:
输入:x = 2.00000, n = 10
输出:1024.00000
示例 2:
输入:x = 2.10000, n = 3
输出:9.26100
示例 3:
输入:x = 2.00000, n = -2
输出:0.25000
解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0-231 <= n <= 231-1n是一个整数- 要么
x不为零,要么n > 0。 -104 <= xn <= 104
思路
这里我们可以使用二分的思想,可以快速提高效率,例如将3的32次方分为两个3的16次方相乘,不断向下递归,最终返回相乘结果,只不过这里需要注意负数和奇偶次方问题需要单独判断。
代码
class Solution {
public:double myPow(double x, int n) {// 如果指数n为负数,将问题转化为计算 x^(-n),即取倒数return n < 0 ? 1.0 / Pow(x, -(long long)n) : Pow(x, n);}double Pow(double x, long long n) {// 递归终止条件:n为0时,任何数的0次方都为1if (n == 0) return 1.0;// 递归调用,计算 x^(n/2)double tmp = Pow(x, n / 2);// 如果n为奇数,返回 tmp * tmp * xif (n % 2)return tmp * tmp * x;else // 如果n为偶数,返回 tmp * tmpreturn tmp * tmp;}
};
return n < 0 ? 1.0 / Pow(x, -(long long)n) : Pow(x, n);:根据指数n的正负情况,决定调用正指数或者取倒数的递归函数。当n为负数时,将其转化为正数计算,并返回结果的倒数。double Pow(double x, long long n):递归函数,用于计算 x^n。if (n == 0) return 1.0;:递归终止条件。当指数n为0时,任何数的0次方都为1。double tmp = Pow(x, n / 2);:递归调用,计算 x^(n/2)。这里利用了指数幂的性质,将问题规模减半,减少了计算量。if (n % 2):判断n是否为奇数。return tmp * tmp * x;:如果n为奇数,返回 tmp * tmp * x,这是因为 x^n = (x(n/2))2 * x。
n) : Pow(x, n);`:根据指数n的正负情况,决定调用正指数或者取倒数的递归函数。当n为负数时,将其转化为正数计算,并返回结果的倒数。double Pow(double x, long long n):递归函数,用于计算 x^n。if (n == 0) return 1.0;:递归终止条件。当指数n为0时,任何数的0次方都为1。double tmp = Pow(x, n / 2);:递归调用,计算 x^(n/2)。这里利用了指数幂的性质,将问题规模减半,减少了计算量。if (n % 2):判断n是否为奇数。return tmp * tmp * x;:如果n为奇数,返回 tmp * tmp * x,这是因为 x^n = (x(n/2))2 * x。return tmp * tmp;:如果n为偶数,返回 tmp * tmp,这是因为 x^n = (x(n/2))2。
相关文章:

算法沉淀——递归(leetcode真题剖析)
算法沉淀——递归 01.汉诺塔问题02.合并两个有序链表03.反转链表04.两两交换链表中的节点05.Pow(x, n) 递归是一种通过调用自身的方式来解决问题的算法。在递归算法中,问题被分解为更小的相似子问题,然后通过对这些子问题的解进行组合来解决原始问题。递…...

BERT模型中的input_ids和attention_mask参数
一、概述 1.1 input_ids 在BERT模型及其衍生体中,输入文本首先经过一个分词处理流程,其中文本被细分为单词或子单词(subwords),每个分词随后映射到一个唯一的整数标识符。这些标识符组成了所谓的input_ids数组&#x…...
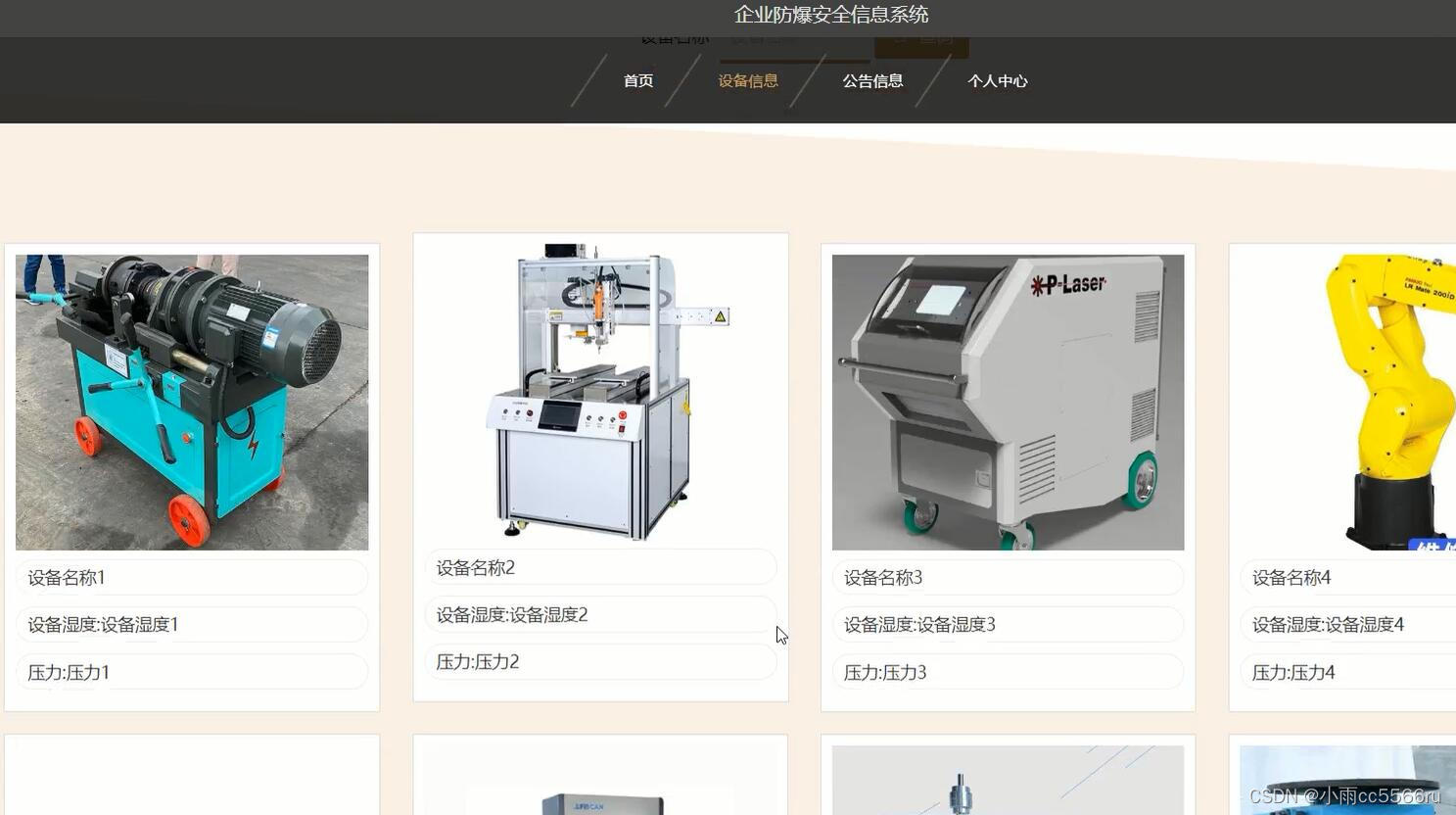
java+vue_springboot企业设备安全信息系统14jbc
企业防爆安全信息系统采用B/S架构,数据库是MySQL。网站的搭建与开发采用了先进的java进行编写,使用了vue框架。该系统从三个对象:由管理员、人员和企业来对系统进行设计构建。主要功能包括:个人信息修改,对人员管理&am…...
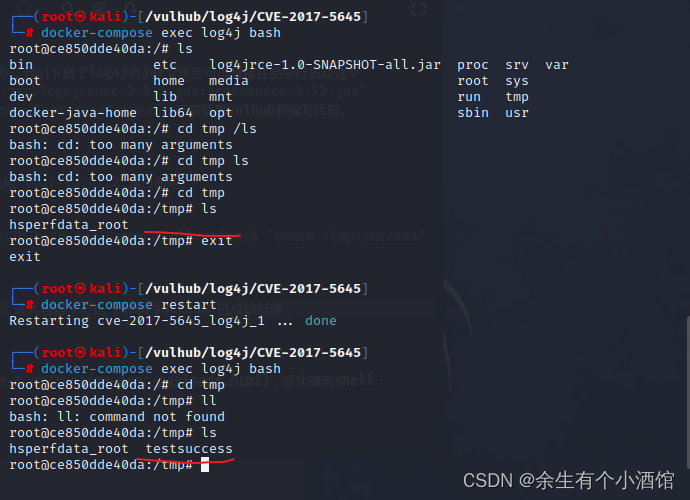
vulhub中Apache Log4j Server 反序列化命令执行漏洞复现(CVE-2017-5645)
Apache Log4j是一个用于Java的日志记录库,其支持启动远程日志服务器。Apache Log4j 2.8.2之前的2.x版本中存在安全漏洞。攻击者可利用该漏洞执行任意代码。 1.我们使用ysoserial生成payload,然后直接发送给your-ip:4712端口即可。 java -jar ysoserial-…...

基于python+django+vue.js开发的医院门诊管理系统/医疗管理系统
功能介绍 平台采用B/S结构,后端采用主流的Python语言进行开发,前端采用主流的Vue.js进行开发。 功能包括:医生管理、科室管理、护士管理、住院管理、药品管理、用户管理、日志管理、系统信息模块。 源码地址 https://github.com/geeeeeee…...

Linux文件系统笔记
文章目录 FILE SYSTEM软硬链接 动静态库 使用别人提供的库 FILE SYSTEM 文件的管理工作: 1.基础知识: 文件 属性 内容不是所有文件都会打开所有的打开的,未打开的文件会进行管理未打开文件,要能做到快速定位文件磁盘–物理存…...
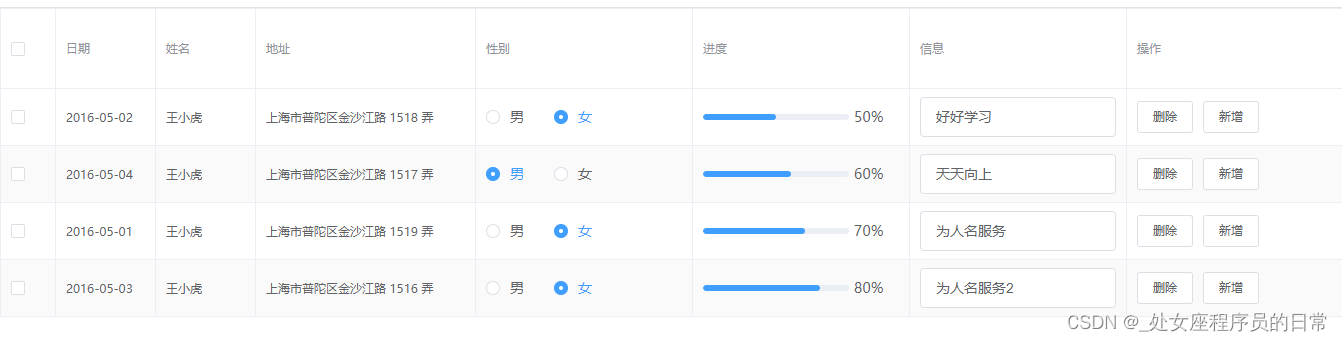
vue封装el-table表格组件
先上效果图: 本文包含了具名插槽、作用域插槽、jsx语法三种: Render.vue(很重要,必须有): <script> export default {name: "FreeRender",functional: true,props: {scope:Object,render: Functio…...

「Python系列」Python数据结构
文章目录 一、数据结构二、相关链接 一、数据结构 Python提供了多种内置的数据结构,这些数据结构在编程中非常有用。以下是Python中常见的一些数据结构: 列表(List): 列表是Python中最常用的数据结构之一,它是一个有…...
MySQL多实例部署:从概念到实操的全面指南
目录 MySQL多实例管理 单实例 什么是多实例 多实例的好处 多实例的弊端 MySQL多实例用在哪些场景 资金紧张的公司 用户并发访问量不大的业务 大型网站也有用多实例 部署MySQL多实例 rpm和源码的优缺点 二进制方式安装mysql 准备二进制mysql运行所需的环境 准备多…...

C++学习Day07之虚函数和纯虚函数
目录 前言一、程序及输出1.1 虚函数1.2 纯虚函数1.2.1 定义、示例1.2.2 引入原因1.2.3 抽象类 二、分析与总结 前言 在 C 中,虚函数和纯虚函数是实现多态性的重要概念。虚函数是在基类中声明为虚函数的函数,在派生类中可以被重写,实现动态联…...
GZ036 区块链技术应用赛项赛题第9套
2023年全国职业院校技能大赛 高职组 “区块链技术应用” 赛项赛卷(9卷) 任 务 书 参赛队编号: 背景描述 随着异地务工人员的增多,房屋租赁成为一个广阔是市场;目前,现有技术中的房屋租赁是由…...
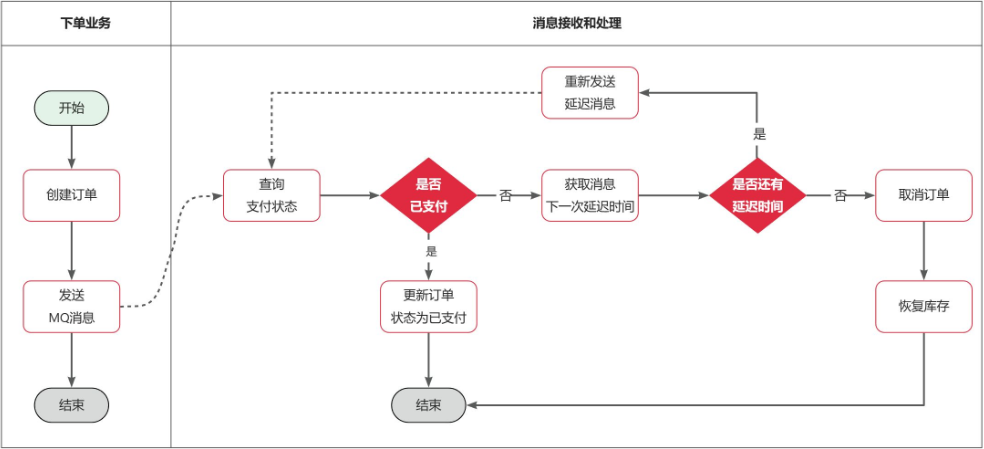
微服务—RabbitMQ高级(延迟消息)
本博客为个人学习笔记,学习网站:2023黑马程序员RabbitMQ入门到实战教程 高级篇章节 目录 延迟消息 死信交换机 延迟消息插件 下载安装 延迟交换机声明 编辑 发送延迟消息 订单状态同步问题 延迟消息 在电商的支付业务中,对于一些库…...

香港服务器如何取消windows的自动更新
大家用过电脑的人对windows系统的自动更新应该都不会陌生,其实香港服务器的使用也是一样的方法。为什么要对香港服 务器windows的自动更新进行关闭呢?其主要原因在于,有些更新是不能更新,一更新话,系统反而会变得不稳定…...
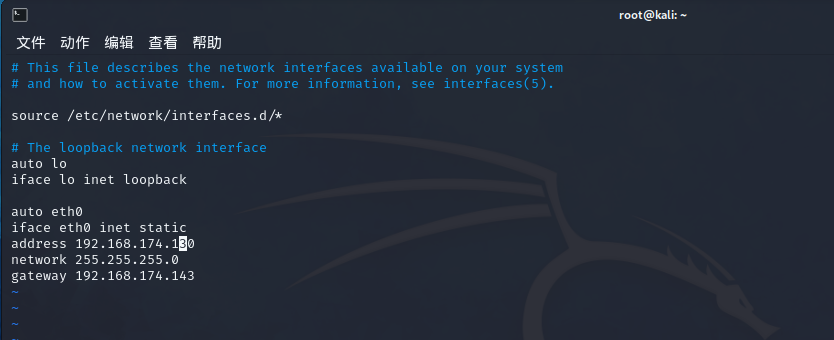
kali虚拟机桥接模式快速设置
第一步:选择 虚拟机 > 设置 > 虚拟机设置,设置桥接模式 不选择复制物理网络连接状态选项: 如果采用DHCP的方式来分配IP地址,当电脑网络从有线或无线网络之间进行移动时,DHCP会重新分配ip地址,即虚拟机…...
02-18:边缘部分源码(源码分析篇))
「连载」边缘计算(十五)02-18:边缘部分源码(源码分析篇)
(接上篇) ChannelContext struct定义如下所示。 KubeEdge/beehive/pkg/core/context/context.go // ChannelContext is object for Context channel type ChannelContext struct { //ConfigFactory goarchaius.ConfigurationFactory channels map[…...
-NoSQL与MySQL的比较)
MySQL性能调优篇(8)-NoSQL与MySQL的比较
MySQL数据库是一种关系型数据库,而NoSQL是一种非关系型数据库。它们在数据存储和处理方式、数据模型和可扩展性等方面存在一些明显的差异。本文将对MySQL数据库和NoSQL进行比较,并介绍它们的优势和劣势。 首先,MySQL使用表格的形式来存储数据…...
【Linux学习】线程池
目录 23.线程池 23.1 什么是线程池 23.2 为什么需要线程池 23.3 线程池的应用场景 23.4 实现一个简单的线程池 23.4.1 RAII风格信号锁 23.4.2 线程的封装 23.4.3 日志打印 22.4.4 定义队列中存放Task类任务 23.4.5 线程池的实现(懒汉模式) 为什么线程池中需要有互斥锁和条件变…...
利用Docker部署一个简单的springboot项目
文章目录 1、首先利用docker部署一个redis中间件1.1、下载redis镜像1.2、在主机创建redis挂载的目录和文件1.3、部署redis中间件 2、创建springboot项目2.1、修改application.yml2.2、编写controller2.3、启动应用并测试访问 3、将应用打包成镜像3.1、编写Dockerfile3.2、上传文…...

【Java】纯小白的三种工厂模式基础知识学习笔记
工厂模式概念 在Java中,工厂模式是一种设计模式,用于创建对象而无需指定明确的类。工厂模式通过定义一个共同的接口或抽象类来创建对象,然后由工厂类根据特定条件或参数来实例化具体的对象。 工厂模式通常包括三种类型:简单工厂…...
Spring Boot 笔记 006 创建接口_注册
1.1 由于返回数据都是以下这种格式,那么久再编写一个result实体类 报错了,原因是没有构造方法 可以使用lombok的注解自动生成,添加无参的构造器和全参的构造器 package com.geji.pojo;import lombok.AllArgsConstructor; import lombok.NoArg…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

React核心概念:State是什么?如何用useState管理组件自己的数据?
系列回顾: 在上一篇《React入门第一步》中,我们已经成功创建并运行了第一个React项目。我们学会了用Vite初始化项目,并修改了App.jsx组件,让页面显示出我们想要的文字。但是,那个页面是“死”的,它只是静态…...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...
