【LeetCode-494】目标和(回溯动归)
目录
LeetCode494.目标和
题目描述
解法1:回溯法
代码实现
解法2:动态规划
代码实现
LeetCode494.目标和
题目链接
题目描述
给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
-
输入:nums: [1, 1, 1, 1, 1], S: 3
-
输出:5
解释:
-
-1+1+1+1+1 = 3
-
+1-1+1+1+1 = 3
-
+1+1-1+1+1 = 3
-
+1+1+1-1+1 = 3
-
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
提示:
-
数组非空,且长度不会超过 20 。
-
初始的数组的和不会超过 1000 。
-
保证返回的最终结果能被 32 位整数存下。
解法1:回溯法
这里目的是找到和为target的数的方法数,并且长度不超过20,所以我开始觉得是不会超时的。这里的index表示遍历的位置,因为不可以重复取值,所以都是遍历的当前的下一个。然后终结条件就是index的值等于nums数组的长度的时候。
代码实现
class Solution {int times = 0;int target = 0;public int findTargetSumWays(int[] nums, int target) {this.target = target;backTracking(0, 0, nums);return times;}
public void backTracking(int index, int sum, int[] nums) {if (index == nums.length) {if (sum == target) times++;return;}
for (int i = index; i < nums.length; i++) {sum += nums[index];backTracking(i+1, sum, nums);sum -= 2*nums[index];backTracking(i+1, sum, nums);return;}}
}解法2:动态规划
如何转化为01背包问题呢。
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,装满容量为x的背包,有几种方法。
这里的x,就是bagSize,也就是我们后面要求的背包容量。
大家看到(target + sum) / 2 应该担心计算的过程中向下取整有没有影响。
这么担心就对了,例如sum 是5,S是2的话其实就是无解的,所以:
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
同时如果 S的绝对值已经大于sum,那么也是没有方案的。
if (abs(target) > sum) return 0; // 此时没有方案
再回归到01背包问题,为什么是01背包呢?
因为每个物品(题目中的1)只用一次!
这次和之前遇到的背包问题不一样了,之前都是求容量为j的背包,最多能装多少。
本题则是装满有几种方法。其实这就是一个组合问题了。
-
确定dp数组以及下标的含义
dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法
其实也可以使用二维dp数组来求解本题,dpi:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dpi种方法。
-
确定递推公式
有哪些来源可以推出dp[j]呢?
只要搞到nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
例如:dp[j],j 为5,
-
已经有一个1(nums[i]) 的话,有 dp[4]种方法 凑成 容量为5的背包。
-
已经有一个2(nums[i]) 的话,有 dp[3]种方法 凑成 容量为5的背包。
-
已经有一个3(nums[i]) 的话,有 dp[2]中方法 凑成 容量为5的背包
-
已经有一个4(nums[i]) 的话,有 dp[1]中方法 凑成 容量为5的背包
-
已经有一个5 (nums[i])的话,有 dp[0]中方法 凑成 容量为5的背包
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
所以求组合类问题的公式,都是类似这种:
dp[j] += dp[j - nums[i]]
这个公式在后面在讲解背包解决排列组合问题的时候还会用到!
-
dp数组如何初始化
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
这里有录友可能认为从dp数组定义来说 dp[0] 应该是0,也有录友认为dp[0]应该是1。
其实不要硬去解释它的含义,咱就把 dp[0]的情况带入本题看看应该等于多少。
如果数组[0] ,target = 0,那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1, 也就是说给数组里的元素 0 前面无论放加法还是减法,都是 1 种方法。
所以本题我们应该初始化 dp[0] 为 1。
可能有同学想了,那 如果是 数组[0,0,0,0,0] target = 0 呢。
其实 此时最终的dp[0] = 32,也就是这五个零 子集的所有组合情况,但此dp[0]非彼dp[0],dp[0]能算出32,其基础是因为dp[0] = 1 累加起来的。
dp[j]其他下标对应的数值也应该初始化为0,从递推公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
-
确定遍历顺序
nums放在外循环,target在内循环,且内循环倒序。
-
举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], S: 3
bagSize = (S + sum) / 2 = (3 + 5) / 2 = 4
代码实现
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i = 0; i < nums.length; i++) sum += nums[i];//如果target过大 sum将无法满足if ( target < 0 && sum < -target) return 0;if ((target + sum) % 2 != 0) return 0;int size = (target + sum) / 2;if(size < 0) size = -size;int[] dp = new int[size + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = size; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[size];}
}相关文章:
)
【LeetCode-494】目标和(回溯动归)
目录 LeetCode494.目标和 题目描述 解法1:回溯法 代码实现 解法2:动态规划 代码实现 LeetCode494.目标和 题目链接 题目描述 给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 和 -。对于数组中…...

力扣 188. 买卖股票的最佳时机 IV
题目来源:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/description/ C题解:动态规划 思路同力扣 123. 买卖股票的最佳时机 III-CSDN博客,只是把最高2次换成k次。如果思路不清晰,可以将k从0写到4等找找规律…...

【Go语言】Go项目工程管理
GO 项目工程管理(Go Modules) Go 1.11 版本开始,官方提供了 Go Modules 进行项目管理,Go 1.13开始,Go项目默认使用 Go Modules 进行项目管理。 使用 Go Modules的好处是不再需要依赖 GOPATH,可以在任意位…...
美容小程序:让预约更简单,服务更贴心
在当今繁忙的生活节奏中,美容预约常常令人感到繁琐和疲惫。为了解决这个问题,许多美容院和SPA中心已经开始采用美容小程序来简化预约流程,并提供更加贴心的服务。在这篇文章中,我们将引导您了解如何制作一个美容小程序,…...

【递归】:原理、应用与案例解析 ,助你深入理解递归核心思想
递归 1.基础简介 递归在计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集 例如 递归遍历环形链表 基本情况(Base Case):基本情况是递归函数中最简单的情况,它们通常是递…...
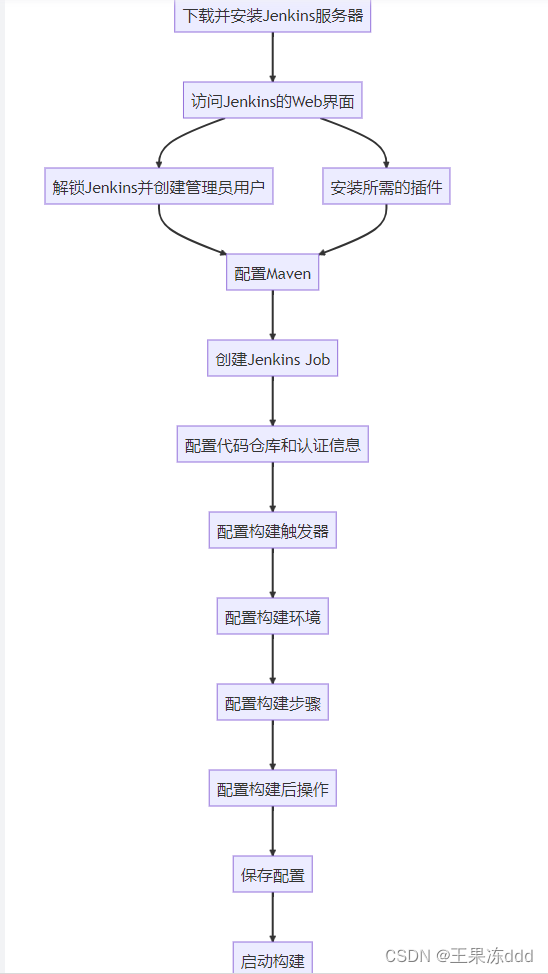
【 Maven 】花式玩法之多模块项目
目录 一、认识Maven多模块项目 二、maven如何定义项目的发布策略 2.1 版本管理 2.2 构建配置 2.3 部署和发布 2.4 依赖管理 2.5 发布流程 三、使用Jenkins持续集成Maven项目 四、总结 如果你有一个多模块项目,并且想将这些模块发布到不同的仓库或目标位置&…...

LeetCode 热题 100 Day01
哈希模块 哈希结构: 哈希结构,即hash table,哈希表|散列表结构。 图摘自《代码随想录》 哈希表本质上表示的元素和索引的一种映射关系。 若查找某个数组中第n个元素,有两种方法: 1.从头遍历,复杂度…...
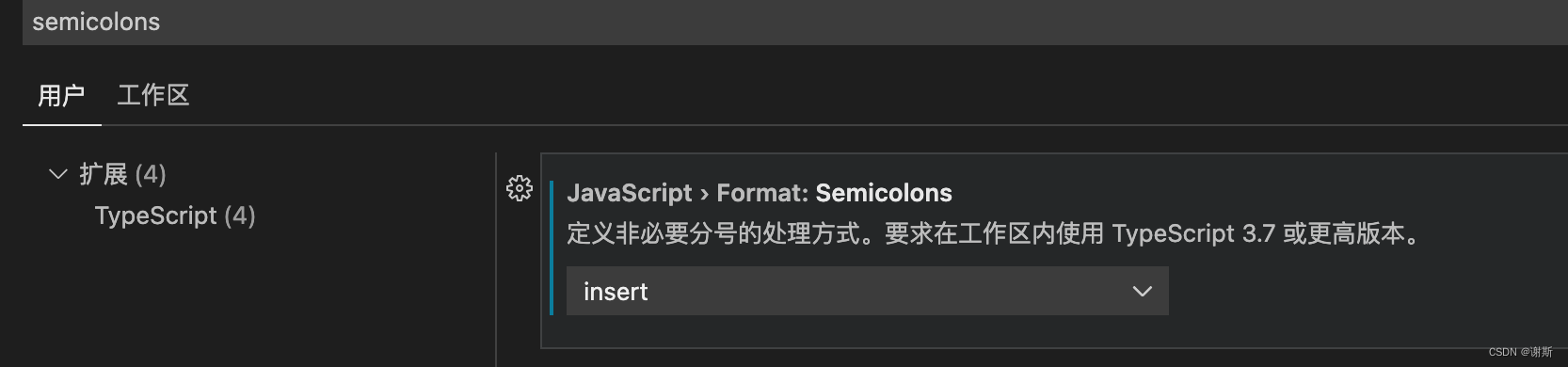
[vscode]vue js部分结尾加分号
设置中寻找 semicolons确定在TypeScript的这个扩展中设置选项为insert...
友点CMS image_upload.php 文件上传漏洞复现
0x01 产品简介 友点CMS是一款高效且灵活的网站管理系统,它为用户提供了简单易用的界面和丰富的功能。无论是企业还是个人,都能通过友点CMS快速搭建出专业且美观的网站。该系统支持多种内容类型和自定义模板,方便用户按需调整。同时,它具备强大的SEO功能,能提升网站在搜索…...

C语言—指针(3)
嘿嘿嘿嘿,你看我像指针吗? 不会写,等我啥时候会写了再说吧,真的累了,倦了 1.面试题 1)定义整形变量i; 2)p为指向整形变量的指针变量; 3)定…...
【八股文】面向对象基础
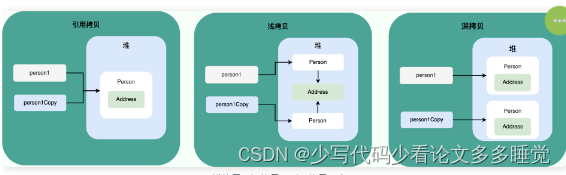
【八股文】面向对象基础 面向对象和面向过程的区别 面向过程把解决问题的过程拆成一个个方法,通过一个个方法的执行解决问题。面向对象会先抽象出对象,然后用对象执行方法的方式解决问题。 创建一个对象用什么运算符?对象实体与对象引用有何不同? …...

Day49 647 回文子串 516 最长回文子序列
647 回文子串 给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。 方法一:动态规划: 采用一个二维的dp数组…...

探秘GNU/Linux Shell:命令行的魔法世界
GNU/Linux的Shell是一种特殊的交互式工具,为用户提供了强大的控制和管理Linux系统的方式。在这个博客中,我们将深入了解Shell的基本概念、功能以及不同类型的Shell。 Shell的本质 Shell的核心是命令行提示符,它是用户与Linux系统进行交互的…...
基于STM32F407的coreJSON使用教程
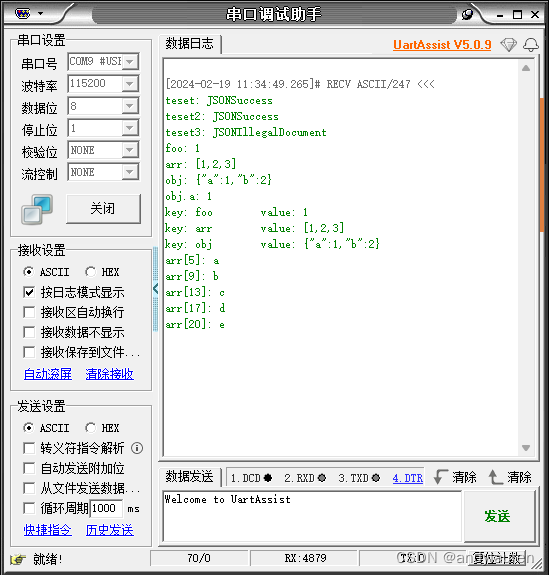
目录 概述 工程建立 代码集成 函数介绍 使用示例 概述 coreJSON是FreeRTOS中的一个组件库,支持key查找的解析器,他只是一个解析器,不能生成json数据。同时严格执行 ECMA-404 JSON 标准。该库用 C 语言编写,设计符合 ISO C90…...
keepalived双主模式测试
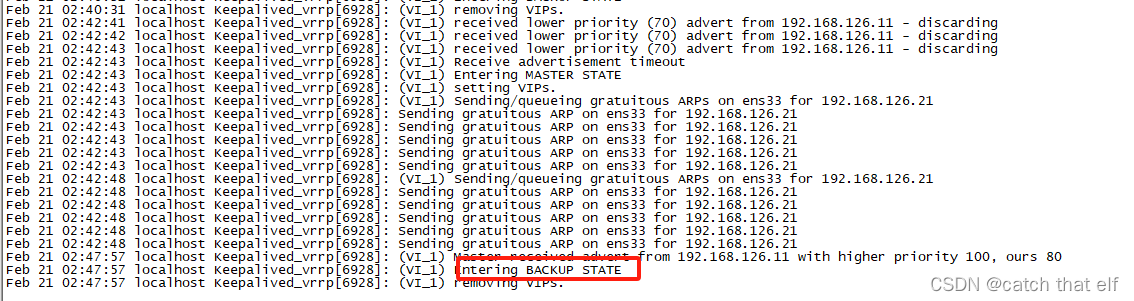
文章目录 环境准备部署安装keepavlived配置启动测试模拟Nginx宕机重新启动问题分析 环境准备 测试一下keepalived的双主模式,所谓双主模式就是两个keepavlied节点各持有一个/组虚IP,默认情况下,二者互为主备,同时对外提供服务&am…...

微服务中的熔断、降级和限流
在现代微服务架构中,熔断、降级和限流是保障系统稳定性和可靠性的重要手段。本文将深入探讨这三种机制在微服务架构中的作用、原理以及实践方法。 1. 熔断(Circuit Breaker) 1.1 作用和原理 熔断器是一种可以在服务发生故障时快速中断请求的机制,防止故障蔓延到整个系统…...

2023年便宜的云服务器分享:最低26元4核16G
2024年阿里云服务器租用价格表更新,云服务器ECS经济型e实例2核2G、3M固定带宽99元一年、ECS u1实例2核4G、5M固定带宽、80G ESSD Entry盘优惠价格199元一年,轻量应用服务器2核2G3M带宽轻量服务器一年61元、2核4G4M带宽轻量服务器一年165元12个月、2核4G服…...

汽车零部件制造业MES系统解决方案
一、汽车零部件行业现状 随着全球汽车产业不断升级,汽车零部件市场竞争日趋激烈,从上游的钢铁、塑料、橡胶等生产到下游的主机厂配套制造,均已成为全球各国汽车制造大佬战略目标调整的焦点,其意欲在汽车零部件行业快速开疆扩土&…...

区块链/加密币/敏感/特殊题材专供外媒发稿,英文多国语言海外新闻营销推广
【本篇由言同数字科技有限公司原创】敏感题材是海外媒体在报道过程中常遇到的难题,需要平衡新闻真实性、公正性与敏感性。本文将探讨海外媒体报道敏感题材所面临的挑战,并介绍如何抓住机遇提高报道质量。 第一部分:敏感题材报道的挑战 报道…...

初识Nginx
摘要:最近几个项目中的接口总是访问受限,需要后端同事配置Nginx代理,了解下Nginx后面自己配置。 Nginx 是一款高性能的开源 Web 服务器和反向代理服务器。它具有轻量级、高并发、低内存消耗等特点,常被用作静态资源服务、负载…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...
