突出最强算法模型——回归算法 !!
文章目录
1、特征工程的重要性
2、缺失值和异常值的处理
(1)处理缺失值
(2)处理异常值
3、回归模型的诊断
(1)残差分析
(2)检查回归假设
(3)Cook's 距离
4、学习曲线和验证曲线的解读
(1)学习曲线
(2)验证曲线
5、解释线性回归的原理
(1)模型表示
(2)损失函数
(3)梯度下降
6、非线性回归模型的例子
(1)多项式回归
(2)指数回归
(3)对数回归
(4)广义可加模型(Generalized Additive Models,GAM)
7、如何处理过拟合
(1)识别过拟合
(2)解决过拟合
1、特征工程的重要性
特征选择是指从所有可用的特征中选择最相关和最有用的特征,以用于模型的训练和预测。而特征工程则涉及对原始数据进行预处理和转换,以便更好地适应模型的需求,包括特征缩放、特征变换、特征衍生等操作。
那么,为什么这两个步骤如此重要呢?从以下4个方面概括:
(1)提高模型性能:通过选择最相关的特征和对特征进行适当的工程处理,可以提高模型的性能。过多的不相关特征会增加模型的复杂性,降低模型的泛化能力,导致过拟合。而合适的特征工程可以帮助模型更好地理解数据的结构和关系,提高模型的准确性。
(2)降低计算成本:在实际的数据集中,可能存在大量的特征,而并非所有特征都对预测目标具有重要影响。通过特征选择,可以减少模型训练的计算成本和时间消耗,提高模型的效率。
(3)减少过拟合风险:过拟合是模型在训练数据上表现很好,但在新数据上表现不佳的现象。特征选择和特征工程可以帮助降低过拟合的风险,使模型更加泛化到未见过的数据上。
(4)提高模型的解释性:经过特征选择和特征工程处理的模型,其特征更加清晰明了,更容易理解和解释。这对于实际应用中的决策和解释至关重要。
常用的特征选择方向包括基于统计检验、正则化方法、基于树模型的方法等;而特征工程则涉及到缺失值处理、标准化、归一化、编码、特征组合、降维等技术。
下面举一个简单的案例,在代码中进行特征选择和特征工程,结合上面所说以及代码中的注释进行理解~
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.feature_selection import SelectKBest, f_regression
from sklearn.preprocessing import StandardScaler# 随机生成示例数据
np.random.seed(0)
X = np.random.rand(100, 5) # 5个特征
y = X[:, 0] + 2*X[:, 1] - 3*X[:, 2] + np.random.randn(100) # 线性关系,加入噪声# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 特征工程:标准化特征
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 特征选择:选择k个最好的特征
selector = SelectKBest(score_func=f_regression, k=3)
X_train_selected = selector.fit_transform(X_train_scaled, y_train)
X_test_selected = selector.transform(X_test_scaled)# 训练回归模型
model = LinearRegression()
model.fit(X_train_selected, y_train)# 在测试集上评估模型性能
score = model.score(X_test_selected, y_test)
print("模型在测试集上的R^2得分:", score)上面代码中 ,我们首先生成了一些示例数据,然后对数据进行了标准化处理。接着,我们使用方差分析选择了3个最佳特征。最后训练了一个线性回归模型并在测试集上评估了其性能。
通过特征选择和特征工程,在实际的算法建模中,可以更好地理解数据,提高模型的性能。
2、缺失值和异常值的处理
(1)处理缺失值
① 数据探索与理解
首先,需要仔细了解数据,确定哪些特征存在缺失值,并理解缺失的原因。
② 缺失值的处理方式
- 删除:如果缺失值占比很小且随机分布,可以考虑删除确实样本或特征。
- 填充:采样统计量(如均值、中位数、众数)进行填充,或者使用插值法(如线性插值、多项式插值)进行填充。
- 模型预测:使用其他特征建立模型来预测缺失值。
③ 代码示例
import pandas as pd
from sklearn.impute import SimpleImputer# 假设 df 是你的数据框
# 使用均值填充缺失值
imputer = SimpleImputer(strategy='mean')
df_filled = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)(2)处理异常值
① 异常值的识别
可以使用可视化工具(如箱线图、直方图)来识别异常值,或者利用统计学方法(如Z分数、IQR)来检测异常值。
② 异常值的处理方式
- 删除:如果异常值数量较少且不影响整体趋势,可以考虑删除异常样本。
- 替换:用特定值(如上下限、中位数、均值)替换异常值,使其不会对模型产生过大影响。
- 转换:对异常值进行转换,使其落入正常范围内。
③ 代码示例
# 假设 df 是你的数据框
# 假设我们使用 Z 分数方法来检测异常值并替换为均值
from scipy import statsz_scores = stats.zscore(df)
abs_z_scores = np.abs(z_scores)
filtered_entries = (abs_z_scores < 3).all(axis=1)
df_no_outliers = df[filtered_entries]总的来说,遇到这种情况,有几点需要注意:
- 处理缺失值和异常值需要谨慎,因为不当的处理可能会影响模型的预测能力。
- 在处理之前,要仔细观察数据的分布和特点,选择合适的处理方法。
- 在处理过程中,要保持对数据的透明度和可解释性,记录下处理过程以及处理后的数据情况。
3、回归模型的诊断
一些常见的回归模型诊断方法:
(1)残差分析
- 残差(Residuals)是指观测值与模型预测值之间的差异。通过分析残差可以评估模型的拟合程度和误差结构。
- 通过绘制残差图(Residual Plot)来检查残差是否随机分布在0附近,若残差呈现明显的模式(如趋势或异方差性),则可能表示模型存在问题。
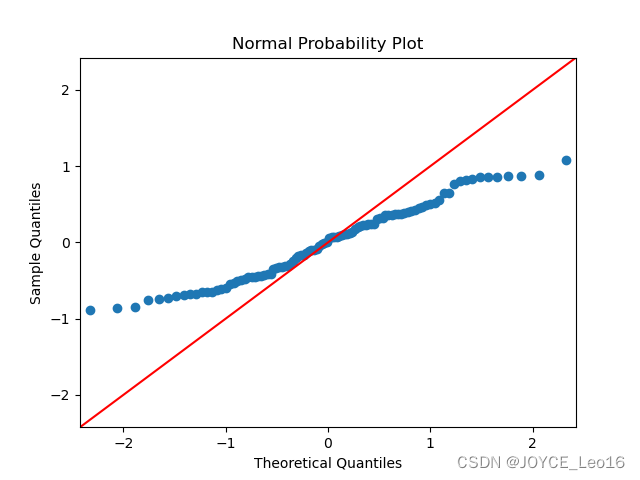
- 正态概率图(Normal Probability Plot)可以用来检查残差是否服从正态分布。若残差点在一条直线上均匀分布,则表明残差近似正态分布。
(2)检查回归假设
- 线性性(Linearity):使用散点图(Scatter Plot)和偏相关图(Partial Residual Plot)来检查自变量和因变量之间的线性关系。
- 同方差性(Homoscedasticity):通过残差图或者利用Breusch-Pagan检验、White检验等来检验残差是否具有同方差性。若残差的方差随着自变量的变化而变化,则可能存在异方差性。
- 独立性(Independence):通过检查残差之间的自相关性来评估观测数据是否相互独立,可以利用Durbin-Waston检验来进行检验。
- 正态性(Normality):利用正态概率图或者Shapiro-Wilk检验来检验残差是否服从正态分布。
(3)Cook's 距离
- Cook's 距离衡量了每个数据点对于模型参数估计的影响程度。大的Cook’s距离可能表示某些数据点对模型拟合具有较大的影响,可能是异常值或者高杆杠点。
用代码来帮助你理解模型诊断相关内容:
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt# 生成示例数据
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 * X.squeeze() + np.random.normal(scale=0.5, size=100)# 添加截距项
X = sm.add_constant(X)# 拟合线性回归模型
model = sm.OLS(y, X).fit()# 残差分析
residuals = model.resid
plt.figure(figsize=(12, 6))# 绘制残差图
plt.subplot(1, 2, 1)
plt.scatter(model.fittedvalues, residuals)
plt.xlabel('Fitted values')
plt.ylabel('Residuals')
plt.title('Residual Plot')# 绘制正态概率图
plt.subplot(1, 2, 2)
sm.qqplot(residuals, line='45')
plt.title('Normal Probability Plot')plt.show()# 检查回归假设
name = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value']
test = sm.stats.diagnostic.het_breuschpagan(residuals, X)
print(dict(zip(name, test)))# Cook's距离
influence = model.get_influence()
cooks_distance = influence.cooks_distance[0]
plt.figure(figsize=(8, 6))
plt.stem(np.arange(len(cooks_distance)), cooks_distance, markerfmt=",", linefmt="b-.")
plt.xlabel('Data points')
plt.ylabel("Cook's Distance")
plt.title("Cook's Distance")
plt.show()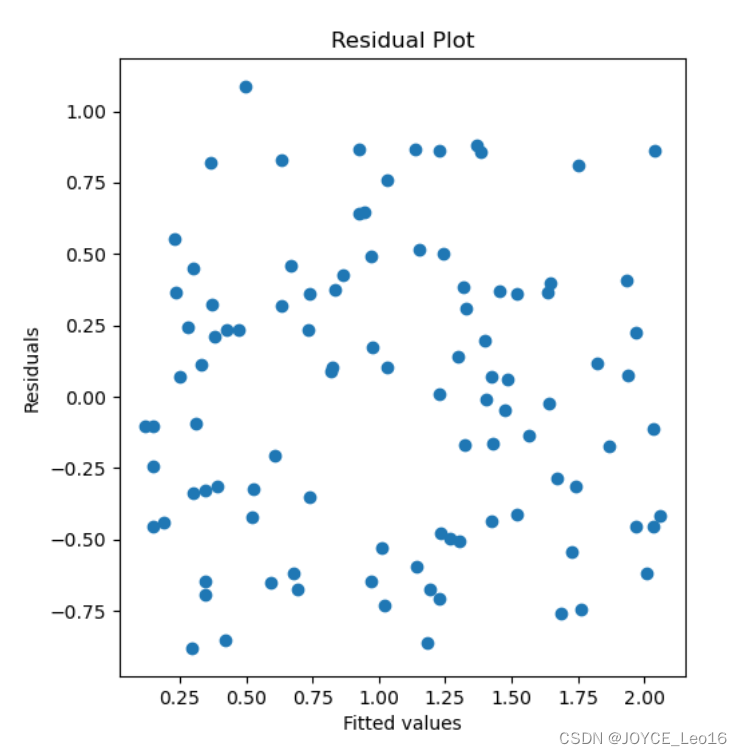

{'Lagrange multiplier statistic': 0.0379899584471155, 'p-value': 0.8454633043549651, 'f-value': 0.03724430837544879, 'f p-value': 0.8473678811756233}
这里给出其中一个结果图,你可以自己执行代码,把其他的图进行打印,以便理解。
通过以上代码以及给出的图形,可以进行残差分析、检查回归假设以及计算Cook's距离,从而对线性回归模型进行全面的诊断。
4、学习曲线和验证曲线的解读
(1)学习曲线
学习曲线(Learning Curve)是一种用于分析模型性能的图表,它展示了训练数据大小与模型性能之间的关系。通常,学习曲线会随着训练数据量的增加而变化。学习曲线的两个关键指标是训练集上的性能和验证集上的性能。
① 学习曲线能告诉我们的信息:
- 欠拟合:如果训练集和验证集上的性能都很差,那么可能是模型过于简单,无法捕捉数据的复杂性。
- 过拟合:如果训练集上的性能很好,但验证集上的性能较差,那么可能是模型过于复杂,学习到了训练集的噪声。
- 合适的模型复杂度:当训练集和验证集上的性能趋于稳定且收敛时,可以认为找到了合适的模型复杂度。
② 如何根据学习曲线调整模型参数:
- 欠拟合时:可以尝试增加模型复杂度,如增加多项式特征、使用更复杂的模型等。
- 过拟合时:可以尝试减少模型复杂度,如减少特征数量、增加正则化、采用更简单的模型等。
(2)验证曲线
验证曲线(Validation Curve)是一种图表,用于分析模型性能与某一参数(例如正则化参数、模型复杂度等)之间的关系。通过在不同参数取值下评估模型的性能,我们可以找到最优的参数取值。
① 验证曲线能告诉我们的信息:
- 最优参数取值:通过观察验证曲线的变化趋势,我们可以确定哪个参数对模型性能有最大的提升。
- 过拟合和欠拟合:验证曲线也可以用于检测过拟合和欠拟合,如果验证集上的性能在某些参数值下出现较大的波动,可能是因为模型处于过拟合或欠拟合状态。
② 如何根据验证曲线调整模型参数:
- 选择最优参数:根据验证曲线的趋势,选择能够使验证集性能最优的参数取值。
- 调整模型复杂度:如果验证曲线显示出模型过拟合或欠拟合,可以相应地调整模型复杂度或正则化参数。
这里,用代码演示了使用学习曲线和验证曲线来评估回归模型,并调整模型参数:
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import learning_curve, validation_curve# 生成随机回归数据
X, y = make_regression(n_samples=1000, n_features=20, noise=0.2, random_state=42)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 定义线性回归模型
estimator = LinearRegression()def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=None, train_sizes=np.linspace(.1, 1.0, 5)):plt.figure()plt.title(title)if ylim is not None:plt.ylim(*ylim)plt.xlabel("Training examples")plt.ylabel("Score")train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)train_scores_mean = np.mean(train_scores, axis=1)train_scores_std = np.std(train_scores, axis=1)test_scores_mean = np.mean(test_scores, axis=1)test_scores_std = np.std(test_scores, axis=1)plt.grid()plt.fill_between(train_sizes, train_scores_mean - train_scores_std,train_scores_mean + train_scores_std, alpha=0.1,color="r")plt.fill_between(train_sizes, test_scores_mean - test_scores_std,test_scores_mean + test_scores_std, alpha=0.1, color="g")plt.plot(train_sizes, train_scores_mean, 'o-', color="r",label="Training score")plt.plot(train_sizes, test_scores_mean, 'o-', color="g",label="Cross-validation score")plt.legend(loc="best")return pltdef plot_validation_curve(estimator, title, X, y, param_name, param_range, cv=None, scoring=None):train_scores, test_scores = validation_curve(estimator, X, y, param_name=param_name, param_range=param_range,cv=cv, scoring=scoring)train_scores_mean = np.mean(train_scores, axis=1)train_scores_std = np.std(train_scores, axis=1)test_scores_mean = np.mean(test_scores, axis=1)test_scores_std = np.std(test_scores, axis=1)plt.title(title)plt.xlabel(param_name)plt.ylabel("Score")plt.ylim(0.0, 1.1)lw = 2plt.plot(param_range, train_scores_mean, label="Training score",color="darkorange", lw=lw)plt.fill_between(param_range, train_scores_mean - train_scores_std,train_scores_mean + train_scores_std, alpha=0.2,color="darkorange", lw=lw)plt.plot(param_range, test_scores_mean, label="Cross-validation score",color="navy", lw=lw)plt.fill_between(param_range, test_scores_mean - test_scores_std,test_scores_mean + test_scores_std, alpha=0.2,color="navy", lw=lw)plt.legend(loc="best")return plt# 使用示例
plot_learning_curve(estimator, "Learning Curve", X_train, y_train, cv=5)
plt.show()
(浅绿色和浅红色区域代表了训练得分和交叉验证得分的标准差,也就是得分的范围。在上述曲线图中,用来展示得分的不确定性或波动性。)
在这段代码中,我们首先定义了一个线性回归模型 LinearRegression(),然后将其传递给了 plot_learning_curve 函数。这样就可以成功绘制学习曲线了。
5、解释线性回归的原理
【数学原理】
(1)模型表示
在线性回归中,我们假设输出变量与输入变量之间存在线性关系。这可以用以下公式表示:
其中:
是输出变量
是输入特征
是模型的系数(也称为权重)
是误差项,表示模型无法解释的部分
(2)损失函数
我们需要定义一个损失函数来衡量模型的预测与实际观测值之间的差异。
在线性回归中,最常见的损失函数是均方误差,其公式是:
其中:
是样本数量
是第
个样本的实际观测值
是第
个样本的模型预测值
(3)梯度下降
梯度下降是一种优化算法,用于最小化损失函数。其思想是通过不断沿着损失函数梯度的反方向更新模型参数,直到达到损失函数的最小值。
梯度下降的更新规则如下:
其中:
是第
个模型参数(系数)
是学习率,控制更新步长
是损失函数关于参数
的偏导数
根据上面提到的理论内容,下面通过代码实现。使用梯度下降算法进行参数优化的Python代码:
import numpy as npclass LinearRegression:def __init__(self, learning_rate=0.01, n_iterations=1000):self.learning_rate = learning_rateself.n_iterations = n_iterationsself.weights = Noneself.bias = Nonedef fit(self, X, y):n_samples, n_features = X.shapeself.weights = np.zeros(n_features)self.bias = 0for _ in range(self.n_iterations):y_predicted = np.dot(X, self.weights) + self.bias# 计算损失函数的梯度dw = (1/n_samples) * np.dot(X.T, (y_predicted - y))db = (1/n_samples) * np.sum(y_predicted - y)# 更新模型参数self.weights -= self.learning_rate * dwself.bias -= self.learning_rate * dbdef predict(self, X):return np.dot(X, self.weights) + self.bias# 使用样例数据进行线性回归
X = np.array([[1, 1.5], [2, 2.5], [3, 3.5], [4, 4.5]])
y = np.array([2, 3, 4, 5])model = LinearRegression()
model.fit(X, y)# 打印模型参数
print("Coefficients:", model.weights)
print("Intercept:", model.bias)# 进行预测
X_test = np.array([[5, 5.5], [6, 6.5]])
predictions = model.predict(X_test)
print("Predictions:", predictions)# Coefficients: [0.37869152 0.65891856]
# Intercept: 0.5604540832879905
# Predictions: [6.07796379 7.11557387]这段代码演示了如何使用梯度下降算法拟合线性回归模型,并进行预测。
6、非线性回归模型的例子
(1)多项式回归
多项式回归是一种将自变量的高次项加入模型的方法,例如:
这与线性回归不同之处在于,自变量的幂次不仅限于一次。通过增加高次项,模型能够更好地拟合非线性关系。
(2)指数回归
指数回归是一种通过指数函数来建模的方法,例如:
这种模型表达了因变量随自变量呈指数增长或指数衰减的趋势。
(3)对数回归
对数回归是一种通过对自变量或因变量取对数来建模的方法,例如:
或者
这种方法适用于当数据呈现出指数增长或衰减的趋势时。
(4)广义可加模型(Generalized Additive Models,GAM)
GAM是一种更一般化的非线性回归模型,它使用非线性函数来拟合每个自变量,例如:
这里的是非线性函数,可以是平滑的样条函数或其他灵活的函数形式。
这里的非线性回归模型与线性回归的主要不同之处在于它们允许了更加灵活的自变量和因变量之间的关系。线性回归假设了自变量和因变量之间的关系是线性的。而非线性回归模型通过引入非线性函数来更好地拟合真实世界中更为复杂的数据关系。这使得非线性模型能够更准确地描述数据,但也可能导致更复杂的模型结构和更难以解释的结果。
下面是一个使用多项式回归的代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures# 生成带噪声的非线性数据
np.random.seed(0)
X = np.linspace(-3, 3, 100)
y = 2 * X**3 - 3 * X**2 + 4 * X - 5 + np.random.normal(0, 10, 100)# 将 X 转换成矩阵形式
X = X[:, np.newaxis]# 使用多项式特征进行变换
poly = PolynomialFeatures(degree=3)
X_poly = poly.fit_transform(X)# 构建并拟合多项式回归模型
model = LinearRegression()
model.fit(X_poly, y)# 绘制原始数据和拟合曲线
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(X_poly), color='red')
plt.title('Polynomial Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.show()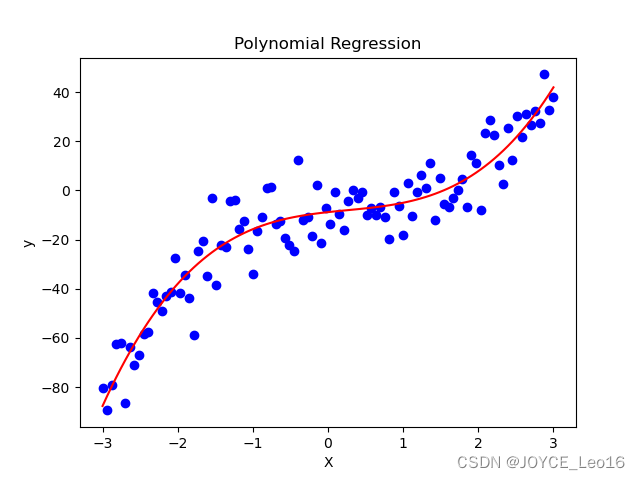
这段代码使用了 PolynomialFeatures 来对自变量进行多项式特征变换,然后使用 LinearRegression 拟合多项式回归模型,并绘制了原始数据和拟合曲线的图像。
7、如何处理过拟合
(1)识别过拟合
- 观察训练误差和验证误差之间的差异。如果训练误差远远低于验证误差,则可能存在过拟合。
- 绘制学习曲线。通过绘制训练误差和验证误差随训练样本数量的变化曲线,可以直观地观察模型是否过拟合。
- 使用交叉验证。通过交叉验证,可以更好地估计模型在未见过的数据上的性能,从而发现过拟合现象。
(2)解决过拟合
- 正则化:通过在损失函数中加入正则项,惩罚模型的复杂度,可以有效地缓解过拟合。常见的正则化方法包括L1正则化(Lasso回归)和L2正则化(岭回归)。
- 减少模型复杂度:降低模型的复杂度,可以减少过拟合的风险。可以通过减少特征数量、降低多项式的阶数等方式来降低模型的复杂度。
- 增加训练数据量:增加训练数据量可以减少模型对训练数据的过度拟合,从而降低过拟合的风险。
- 特征选择:选择最具代表性的特征,去除对模型预测影响较小的特征,可以有效降低模型的复杂度,减少过拟合的风险。
下面是一个使用岭回归来解决回归模型过拟合问题的示例代码:
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error
import numpy as np
import matplotlib.pyplot as plt# 生成一些模拟数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 特征缩放
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)# 使用岭回归解决过拟合问题
ridge_reg = Ridge(alpha=1) # alpha为正则化参数
ridge_reg.fit(X_train_scaled, y_train)# 计算在训练集和测试集上的均方误差
train_error = mean_squared_error(y_train, ridge_reg.predict(X_train_scaled))
test_error = mean_squared_error(y_test, ridge_reg.predict(X_test_scaled))print("训练集均方误差:", train_error)
print("测试集均方误差:", test_error)# 绘制学习曲线
alphas = np.linspace(0, 10, 100)
train_errors = []
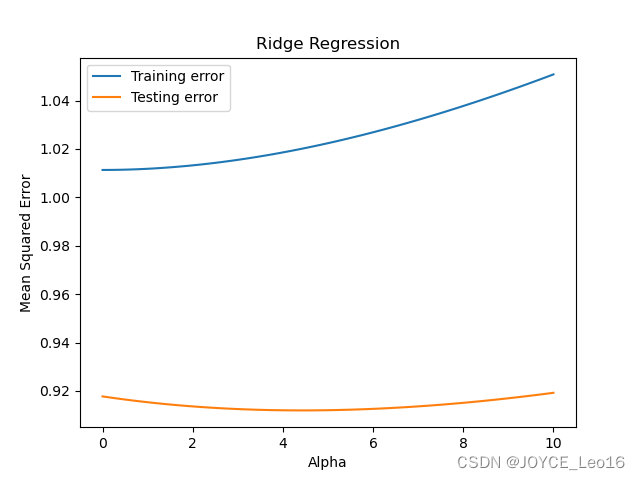
test_errors = []for alpha in alphas:ridge_reg = Ridge(alpha=alpha)ridge_reg.fit(X_train_scaled, y_train)train_errors.append(mean_squared_error(y_train, ridge_reg.predict(X_train_scaled)))test_errors.append(mean_squared_error(y_test, ridge_reg.predict(X_test_scaled)))plt.plot(alphas, train_errors, label='Training error')
plt.plot(alphas, test_errors, label='Testing error')
plt.xlabel('Alpha')
plt.ylabel('Mean Squared Error')
plt.title('Ridge Regression')
plt.legend()
plt.show()在这个示例中,我们使用岭回归来解决过拟合问题。通过调整正则化参数alpha,我们可以控制正则化的程度,从而调节模型的复杂度,避免过拟合。
最后,通过绘制学习曲线,我们可以直观地观察到模型在不同正则化参数下的表现,从而选择合适的参数值。
训练集均方误差: 1.0118235703301761
测试集均方误差: 0.9153486918052115
参考:深夜努力写Python
相关文章:

突出最强算法模型——回归算法 !!
文章目录 1、特征工程的重要性 2、缺失值和异常值的处理 (1)处理缺失值 (2)处理异常值 3、回归模型的诊断 (1)残差分析 (2)检查回归假设 (3)Cooks 距离 4、学…...
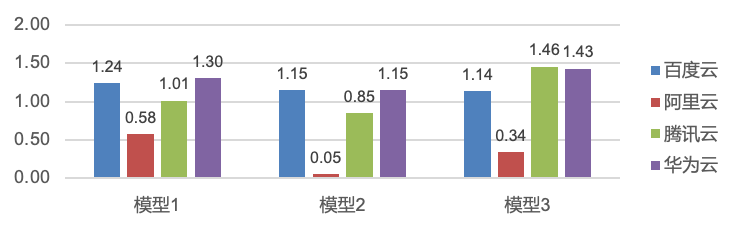
云数据库 Redis 性能深度评测(阿里云、华为云、腾讯云、百度智能云)
在当今的云服务市场中,阿里云、腾讯云、华为云和百度智能云都是领先的云服务提供商,他们都提供了全套的云数据库服务,其中 Redis属于RDS 之后第二被广泛应用的服务,本次测试旨在深入比较这四家云服务巨头在Redis云数据库性能方面的…...

Android---Retrofit实现网络请求:Java 版
简介 在 Android 开发中,网络请求是一个极为关键的部分。Retrofit 作为一个强大的网络请求库,能够简化开发流程,提供高效的网络请求能力。 Retrofit 是一个建立在 OkHttp 基础之上的网络请求库,能够将我们定义的 Java 接口转化为…...

使用静态CRLSP配置MPLS TE隧道
正文共:1591 字 13 图,预估阅读时间:4 分钟 静态CRLSP(Constraint-based Routed Label Switched Paths,基于约束路由的LSP)是指在报文经过的每一跳设备上(包括Ingress、Transit和Egress…...

gentoo安装笔记
最近比较闲,所以挑战一下自己,在自己的台式电脑上安装gentoo 下面记录了我亲自安装的步骤,作为以后我再次安装时参考所用。 整体步骤 一般来将一个linux发行版的安装步骤其实大体上都差不多,基本分为一下几步: 1. …...

Git如何使用 五分钟快速入门
Git如何使用 五分钟快速入门 Git是一个分布式版本控制系统,它可以帮助开发人员跟踪和管理项目的代码变更。与传统的集中式版本控制系统(如SVN)不同,Git允许开发人员在本地存储完整的代码仓库,并且可以独立地进行代码修…...

FreeRTOS学习笔记——(FreeRTOS临界段代码保护及调度器挂起与恢复)
这里写目录标题 1,临界段代码保护简介(熟悉)2,临界段代码保护函数介绍(掌握)3,任务调度器的挂起和恢复(熟悉) 1,临界段代码保护简介(熟悉…...
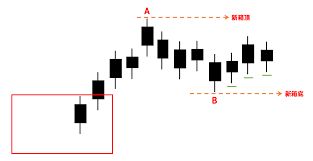
箱形理论在交易策略中的实战应用与优化
箱形理论,简单来说,就是将价格波动分成一段一段的方框,研究这些方框的高点和低点,来推测价格的趋势。 在上升行情中,价格每突破新高价后,由于群众惧高心理,可能会回跌一段,然后再上升…...
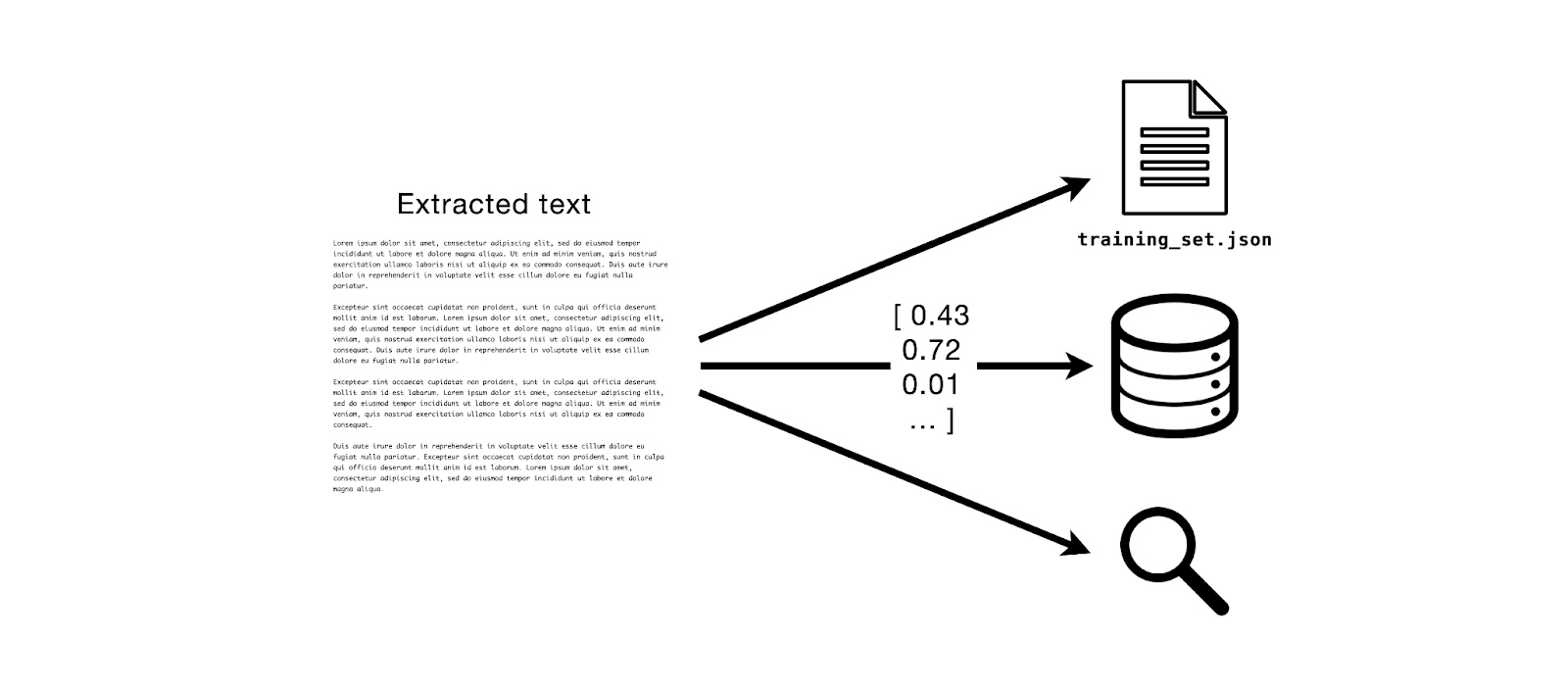
MinIO 和 Apache Tika:文本提取模式
Tl;dr: 在这篇文章中,我们将使用 MinIO Bucket Notifications 和 Apache Tika 进行文档文本提取,这是大型语言模型训练和检索增强生成 LLM和RAG 等关键下游任务的核心。 前提 假设我想构建一个文本数据集,然后我可以用它来微调 LLM.为了做…...
)
c编译器学习05:与chibicc类似的minilisp编译器(待续)
minilisp项目介绍 项目地址:https://github.com/rui314/minilisp 作者也是rui314,commits也是按照模块开发提交的。 minilisp只有一个代码文件:https://github.com/rui314/minilisp/blob/master/minilisp.c 加注释也只有996行。 代码结构&a…...
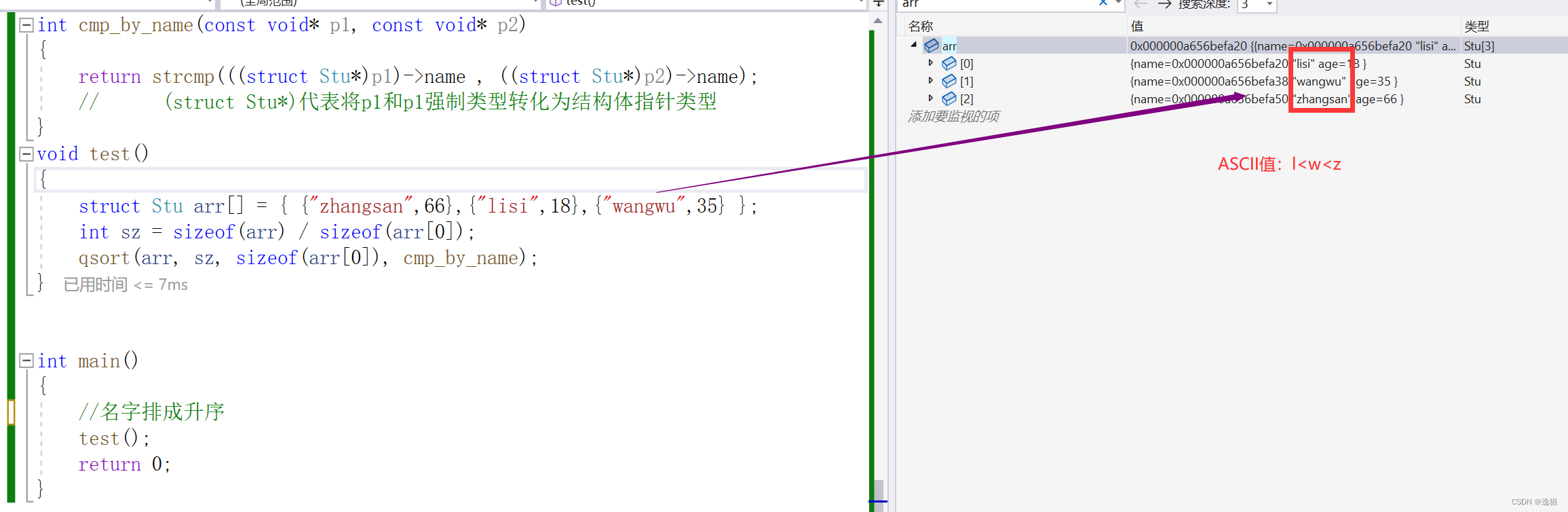
手撕qsort函数
前言 本篇主要讲解的是qsort函数细节以及运用实例。 紧跟我的脚步一起手撕qsort函数吧~ 欢迎关注个人主页:逸狼 更多优质内容: 拿捏c语言指针(上) 拿捏c语言指针(中) 拿捏c语言指针(下&…...

项目在linux上的简单部署
本文章只介绍项目的简单部署,暂时没有Docker部署。 项目部署有两种方式,一种是直接命令部署,第二种是用脚本,脚本本身也是将命令进行封装来执行。 命令 项目通过maven打包,启动命令: # 启动命令 nohup …...
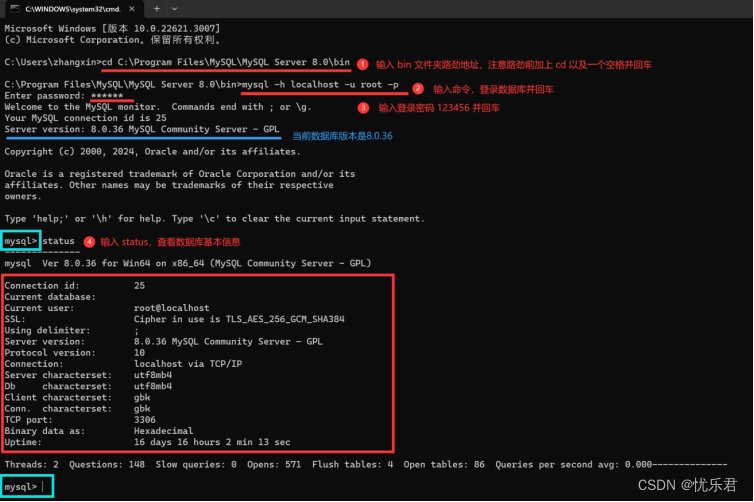
MySQL安装教程(详细版)
今天分享的是Win10系统下MySQL的安装教程,打开MySQL官网,按步骤走呀~ 宝们安装MySQL后,需要简单回顾一下关系型数据库的介绍与历史(History of DataBase) 和 常见关系型数据库产品介绍 呀,后面就会进入正式…...
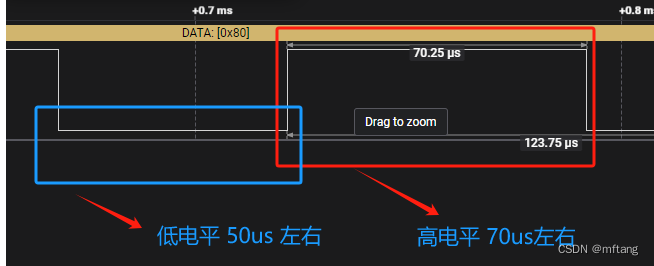
Linux platform tree下的单总线驱动程序设计(DHT11)
目录 概述 1 认识DHT11 1.1 DHT11特性 1.2 DHT11数据格式 1.3 DHT11与MCU通信 1.4 DHT11信号解析 1.4.1 起始信号 1.4.2 解析信号0 1.4.3 解析信号1 2 驱动开发 2.1 硬件接口 2.2 更新设备树 2.2.1 添加驱动节点 2.2.2 编译.dts 2.2.3 更新板卡中的.dtb 2.3 驱…...
)
自研爬虫框架的经验总结(理论及方法)
背景: 由于业务需要,承接一部分的数据采集工作。目前市场内的一些通用框架不太适合。故而进行了自研。 对比自研和目前成熟的框架,自研更灵活适配,可以自己组装核心方法;后者对于新场景的适配需要对框架本身有较高的理…...

配置基于 AWS CRT 的 HTTP 客户端
基于 AWS CRT 的 HTTP 客户端包括同步 AwsCrtHttpClient 和异步 AwsCrtAsyncHttpClient。基于 AWS CRT 的 HTTP 客户端具有以下 HTTP 客户端优势: 更快的 SDK 启动时间 更小的内存占用空间 降低的延迟时间 连接运行状况管理 DNS 负载均衡 SDK 中基于 AWS CRT …...
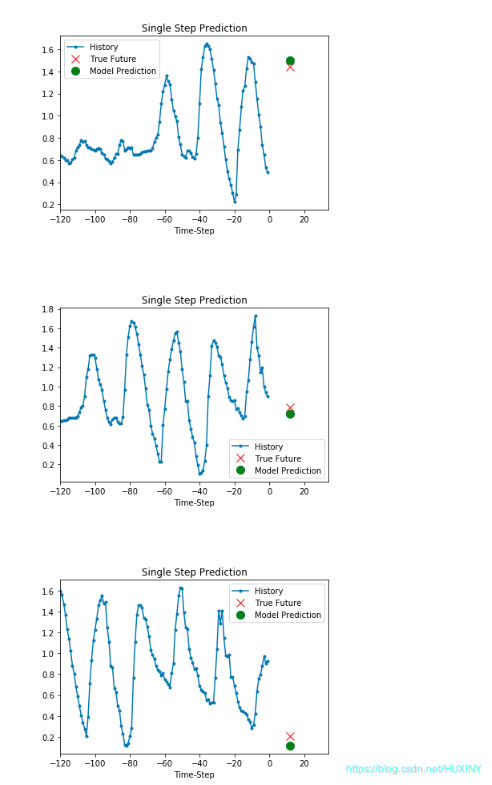
挑战杯 基于LSTM的天气预测 - 时间序列预测
0 前言 🔥 优质竞赛项目系列,今天要分享的是 机器学习大数据分析项目 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng-senior/po…...
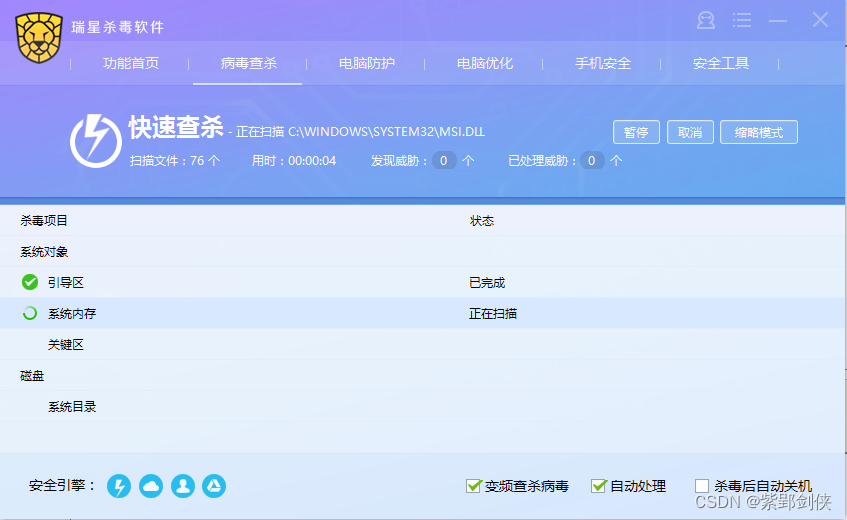
我为什么不喜欢关电脑?
程序员为什么不喜欢关电脑? 你是否注意到,程序员们似乎从不关电脑?别以为他们是电脑上瘾,实则是有他们自己的原因!让我们一起揭秘背后的原因,看看程序员们真正的“英雄”本色! 一、上大学时。 …...

Unity【角色/摄像机移动控制】【1.角色移动】
本文主要总结实现角色移动的解决方案。 1. 创建脚本:PlayerController 2. 创建游戏角色Player,在Player下挂载PlayerController脚本 3. 把Camera挂载到Player的子物体中,调整视角,以实现相机跟随效果 3. PlayerController脚本代码…...

Oracle12cR2之Job定时作业调度器详解
Oracle12cR2之Job定时作业调度器详解 文章目录 Oracle12cR2之Job定时作业调度器详解1.Oracle Job1. 关于Job2. 使用方法 2. Job详细说明1. 查看Job的相关视图2.SYS.DBA_JOBS视图字段详细说明 3. 创建及查看Job1. 创建Job2. 查看运行中的Job 1.Oracle Job 1. 关于Job 在 Oracle…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
