CSS的伪类选择器:nth-child()
CSS的伪类选择器:nth-child()
CSS的伪类选择器 :nth-child() 是一个非常强大的工具,它允许你根据元素在其父元素中的位置(序数)来选择特定的子元素。这个选择器可以应用于任何元素,并且可以与类型选择器、类选择器或ID选择器结合使用。
:nth-child() 选择器接受一个参数,该参数可以是整数、关键字(even 或 odd)或公式(如 an+b)。
- 正整数:直接选择第n个子元素。不能为负数, 不能倒数
例如p:nth-child(2)选择每个父元素中的第二个<p>子元素。th:nth-child(66)选择第66个<th>- 不能用 nth-child(-1)选择倒数第一
- 关键字:
even选择偶数子元素,odd选择奇数子元素。例如,tr:nth-child(even)选择表格中的偶数行。even等效2nodd等效2n+1
- 公式:使用形如
an+b的公式来选择元素。
a是整数。b是正整数, a可正负, b只能正,
an可以理解为步长, 正数n就是向后, 负数n就是向前, 零n如同省略n
例如,:nth-child(0n+1)等同:nth-child(1)等同:first-child选择第一个nth-child(n+5)等同:nth-child(1n+5)选择第五个到最后一个nth-child(-n+10)等同nth-child(-1n+10)倒选第十个到第一个- 合起来用
:nth-child(n+5):nth-child(-n+10)选第五到第十个 li:nth-child(2n+1)等同li:nth-child(odd)选择每个父元素中的奇数<li>子元素(即第1个、第3个、第5个等)。3n+1选择 1,4,7,10…4n+1选择 1,5,9,13…4n+2选择 2,6,10,14…-4n+16表示从16向前,步长为4, 选择 16,12,8,4
请注意,:nth-child() 选择器是基于1的索引,即第一个子元素的索引是1。css的:nth-child(1)相当于js的children[0]
下面是一些使用 :nth-child() 选择器的示例:
/* 选择每个父元素中的第三个子元素,如果它是一个<li>元素 */
ul li:nth-child(3) {color: red; /* 第三个列表项将显示为红色 */
}/* 选择每个父元素中的偶数子元素,如果它是一个<li>元素 */
ul li:nth-child(even) {background-color: lightgray; /* 偶数列表项将有灰色背景 */
}/* 使用公式选择子元素。这将选择第1个,第4个,第7个等... 如果它是一个<li>元素 */
ul li:nth-child(3n+1) {font-weight: bold; /* 符合公式的列表项将加粗显示 */
}
你也可以将 :nth-child() 选择器与其他选择器结合使用,以选择具有特定属性或属于特定类的元素的子元素。例如:
/* 选择类为.items的列表中的第三个<li>子元素 */
ul.items li:nth-child(3) {color: green; /* .items类中的第三个列表项将显示为绿色 */
}
在这个例子中,ul.items li:nth-child(3) 选择器将选择类为 .items 的 <ul> 元素中的第三个 <li> 子元素,并将其文本颜色设置为绿色。
CSS的伪类选择器:nth-child()的用法示例
n可以+- , 右边数字只能+
第一到第六的td : td:nth-child(n+1):nth-child(-n+6)
td:nth-child(n+1):nth-child(-n+6)
第二到第八的a : a:nth-child(n+2):nth-child(-n+8)
a:nth-child(n+2):nth-child(-n+8)
1等效0n+1 , 7等效0n+7 , 没有负数,不能倒数
第一个a : (1) 或 (0n+1)
a:nth-child(1)
a:nth-child(0n+1)
第七个a : (7) 或 (0n+7)
a:nth-child(7)
a:nth-child(0n+7)
想"-1",“0n-1”,“-7”,"0n-7"从倒数开始是行不通的
第三个及之后的a : (n+3)
a:nth-child(n+3)
前七个a, 第七个及之前的a : (-n+7)
a:nth-child(-n+7)
第三到第七之间的a : a:nth-child(n+3):nth-child(-n+7)
a:nth-child(n+3):nth-child(-n+7)
奇数行 : tr:nth-child(2n+1) 或 tr:nth-child(odd)
tr:nth-child(2n+1)
tr:nth-child(odd)
偶数行 : tr:nth-child(2n) 或 tr:nth-child(even)
tr:nth-child(2n)
tr:nth-child(even)
第2,12,22,32,42,52… 以10个递增 : 10n+2
:nth-child(10n+2)
第52个及之前: 2,12,22,32,42,52… 以10个递减 : -10n+52
:nth-child(-10n+52)
MDN Web 开发技术 :nth-child()
选择器示例
tr:nth-child(odd) or tr:nth-child(2n+1)
表示 HTML 表格中的奇数行:1、3、5……。
tr:nth-child(even) or tr:nth-child(2n)
表示 HTML 表格中的偶数行:2、4、6……。
:nth-child(7)
表示第 7 个元素。
:nth-child(5n)
表示第 5、10、15……个元素。第一个匹配的元素是 0 [=5x0],但由于元素的索引是从 1 开始的而 n 从 0 开始,所以不会匹配任何元素。这乍一看可能有点奇怪,但是当公式中的 B 部分为 >0 的值时,就会变得更有意义,就像下面的示例一样。
:nth-child(n+7)
表示第七个及其之后的元素:7 [=0+7]、8 [=1+7]、9 [=2+7],等等。
:nth-child(3n+4)
表示第 4 [=(3×0)+4]、7 [=(3×1)+4]、10 [=(3×2)+4]、13 [=(3×3)+4]……个元素。
:nth-child(-n+3)
表示前三个元素。[=-0+3、-1+3、-2+3]
p:nth-child(n)
表示兄弟元素列表中的每个 <p> 元素。这与简单的 p 选择器选择的元素相同(尽管具有更高的优先级)。
p:nth-child(1) 或 p:nth-child(0n+1)
表示每一个兄弟元素列表中的第一个 <p> 元素。这与 :first-child 选择器相同(并且具有相同的优先级)。
p:nth-child(n+8)``:nth-child(-n+15)
表示兄弟元素列表中的第 8 到第 15 个,且为 <p> 元素的元素。
相关文章:
)
CSS的伪类选择器:nth-child()
CSS的伪类选择器:nth-child() CSS的伪类选择器 :nth-child() 是一个非常强大的工具,它允许你根据元素在其父元素中的位置(序数)来选择特定的子元素。这个选择器可以应用于任何元素,并且可以与类型选择器、类选择器或ID选择器结合…...

python celery使用队列
在celery的配置方法中有个参数叫task_routes,是用来设置不同的任务 消费不同的队列(也就是路由)。 格式如下: { ‘task name’: { ‘queue’: ‘queue name’ }}直接上代码,简单明了,目录格式如下&#x…...

四非保研之旅
大家好,我是工藤学编程,虽有万分感概,但是话不多说,先直接进入正题,抒情环节最后再说,哈哈哈 写在开头 我的分享是来给大家涨信心的,网上的大佬们都太强了,大家拿我涨涨信心&#…...
基于Java+SpringBoot的旅游路线规划系统(源码+论文)
文章目录 目录 文章目录 前言 一、功能设计 二、功能实现 1.1 前端首页模块的实现 1.2 景点新闻 1.3 景点在线预订 1.4 酒店在线预订 1.5 管理员景点管理 1.6 管理员旅游线路管理 1.7 酒店信息管理 三、库表设计 前言 随着我国的经济的不断发展,现在的一些热门的景…...

AI与测试自动化:未来已来
AI与测试自动化注定融合。软件开发的速度和准确性要求已经远远超出了预期。测试自动化通过重复、详细和数据密集型测试来解决这个问题,确保敏捷和持续交付环境中的软件质量。AI的学习、适应和预测能力以完美的效率和准确性增强了测试自动化。复杂的算法现在充当质量…...
—张量》)
深度学习基础之《TensorFlow框架(6)—张量》
一、张量 1、什么是张量 张量Tensor和ndarray是有联系的,当我们print()打印值的时候,它返回的就是ndarray对象 TensorFlow的张量就是一个n维数组,类型为tf.Tensor。Tensor具有以下两个重要的属性: (1)typ…...

第三百六十六回
文章目录 1. 概念介绍2. 使用方法2.1 List2.2 Map2.3 Set 3. 示例代码4. 内容总结 我们在上一章回中介绍了"convert包"相关的内容,本章回中将介绍collection.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章回中介绍的内容是col…...
Fiddler工具 — 18.Fiddler抓包HTTPS请求(一)
1、Fiddler抓取HTTPS过程 第一步:Fiddler截获客户端发送给服务器的HTTPS请求,Fiddler伪装成客户端向服务器发送请求进行握手 。 第二步:服务器发回相应,Fiddler获取到服务器的CA证书, 用根证书(这里的根证…...

多租户数据库的缓冲区共享和预分配方案设计
多租户数据库的缓冲区共享和预分配方案设计 文章目录 多租户数据库的缓冲区共享和预分配方案设计简介初始化输入交互输出输入部分的输出交互部分的输出 评分注意点语言要求需要使用的模块系统框架图方案设计初始化阶段交互阶段 修改进度规划最终代码 简介 云计算技术使企业能够…...
C++:C++入门基础
创作不易,感谢三连 !! 一、什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机ÿ…...

利用System.Web.HttpRuntime.Cache制作缓存工具类
用到的依赖介绍 当谈到 ASP.NET 中的缓存管理时,常涉及到以下三个类:CacheDependency、HttpRuntime.Cache 和 System.Web.Caching。 CacheDependency(缓存依赖项): CacheDependency 类用于指定一个或多个文件或目录作…...
)
266.【华为OD机试真题】抢7游戏(深度优先搜索DFS-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-抢7游戏二.解题思路三.题解代码Python题解代码…...
工具分享:在线键盘测试工具
在数字化时代,键盘作为我们与计算机交互的重要媒介之一,其性能和稳定性直接影响到我们的工作效率和使用体验。为了确保键盘的每个按键都能正常工作,并帮助用户检测潜在的延迟、连点等问题,一款优质的在线键盘测试工具显得尤为重要…...
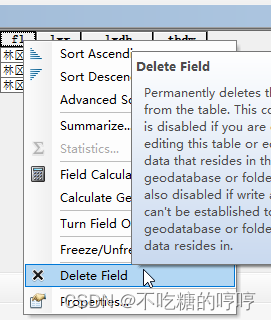
Arcmap excel转shp
使用excel表格转shp的时候,如果你的excel里面有很多字段,直接转很大概率会出现转换结果错误的情况,那么就需要精简一下字段的个数。将原来的表格文件另存一份,在另存为的文件中只保留关键的经度、纬度、和用于匹配的字段即可&…...

14. rk3588自带的RKNNLite检测yolo模型(python)
首先将文件夹~/rknpu2/runtime/RK3588/Linux/librknn_api/aarch64/下的文件librknnrt.so复制到文件夹/usr/lib/下(该文件夹下原有的文件librknnrt.so是用来测试resnet50模型的,所以要替换成yolo模型的librknnrt.so),如下图所示&am…...

心理辅导|高校心理教育辅导系统|基于Springboot的高校心理教育辅导系统设计与实现(源码+数据库+文档)
高校心理教育辅导系统目录 目录 基于Springboot的高校心理教育辅导系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、学生功能模块的实现 (1)学生登录界面 (2)留言反馈界面 (3)试卷列表界…...
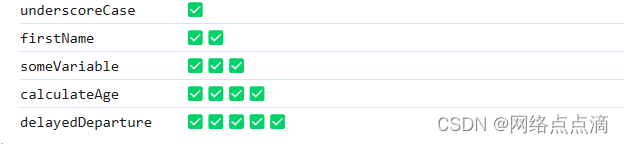
字符串方法挑战
题目 编写一个程序,接收一个使用下划线命名法(underscore_case)编写的变量名列表,并将它们转换为驼峰命名法(camelCase)。 输入将来自插入到DOM中的文本区域(请参见下面的代码)&…...

vivado FIR Filters
Vivado合成直接从RTL中推导出乘加级联来组成FIR滤波器。这种滤波器有几种可能的实现方式;一个例子是收缩滤波器在7系列DSP48E1 Slice用户指南(UG479)中进行了描述,并在8抽头偶数中显示对称收缩FIR(Verilog)…...

c# Contains方法-检查集合中是否包含指定的元素
Contains 是 .NET 集合框架中许多集合类(如 List、Array、HashSet 等)提供的一种方法,用于检查集合中是否包含指定的元素。对于 List<int> 类型,Contains 方法会遍历列表中的所有元素,并判断传入的方法参数是否存…...

【开源】在线办公系统 JAVA+Vue.js+SpringBoot+MySQL
目录 1 功能模块1.1 员工管理模块1.2 邮件管理模块1.3 人事档案模块1.4 公告管理模块 2 系统展示3 核心代码3.1 查询用户3.2 导入用户3.3 新增公告 4 免责声明 本文项目编号: T 001 。 \color{red}{本文项目编号:T001。} 本文项目编号:T001。…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
