面试经典150题——矩阵置零
"Dream it. Wish it. Do it." - Unknown

1. 题目描述

2. 题目分析与解析
2.1 思路一——暴力求解
思路一很简单,就是尝试遍历矩阵的所有元素,如果发现值等于0,就把当前行与当前列的值分别置为0。同时我们需要注意,因为如果出现下图所示的情况:

比如发现matrix[0][0]等于0,我们把第一列和第一行置为0,但是被置为0的行的最后一个元素如上红色框原本也为0,所以这一行与列也要置为0,如果我们单纯把当前行与列覆盖就不知道原来的位置是什么值。并且如果不使用额外空间,我们比如把某一行某一列都置为了0,那么我们在后续遍历时发现这一行这一列的所有元素都为0,都需要处理,那肯定是错误的。所以这就要求我们必须把原始矩阵存储起来。使用额外的O(MN)空间。
2.2 思路二——优化
因为题目中告诉我们仅需要把是matrix中值为0的所在行与所在列元素置为0,那么如果要减少额外的空间使用,我们是不是就可以先遍历matrix单独只存储为0的部分的行列值,然后再将这些为0的值的行列一个个设置为0?这样使用的额外空间就是根据矩阵中为0的元素的个数来计算的。
但是想象一下最坏的情况,如果所有矩阵元素都为0,那么我们是不是就需要M*N个行列,也就是 M*N*2的额外空间大小,那不是还没第一种方法用的额外空间小?
但是如果我们不存储行与列,而是存储当前行与列是否需要置为0的真假,可不可以?如果我们遇到某一个值为0,那么我们就将两个数组的对应第 i 和第二个数组的第 j 个位置置为true,表示我们 i 行,j 列需要置为0,那么即使后续遍历到了其它在当前行或者当前列的某一个值为0的元素,通过查看数组,肯定有一个值为true,只需要把它所单独在的行或者列对应数组的位置置为true就可以。
所以本质上这种方法就是采用两个数组,来表示哪一行需要置为0,哪一列需要置为0。然后再根据数组的真假,将对应行与列置为0。
这种方法会使用O(m + n) 的额外空间。
2.3 思路三——优化2
因为题目提示了
你能想出一个仅使用常量空间的解决方案吗?
那说明肯定有更好的方案,所以我们再想一想。
抓住问题的本质,我们问题的本质不是找哪个元素的值为0,我们的本质是需要将值为0的行于列的元素置为0。并且以前都是空间换时间,现在想要减小空间,那么是不是可以用时间换空间?
根据我的理解,时间与空间实际上就是对于信息的存储形式,而信息总量不变,因此时间增大那么空间就肯定可以变小,时间减小那么额外的信息就需要使用空间来存储。(当然这要建立在完美的算法上,并且也仅仅是个人的理解)
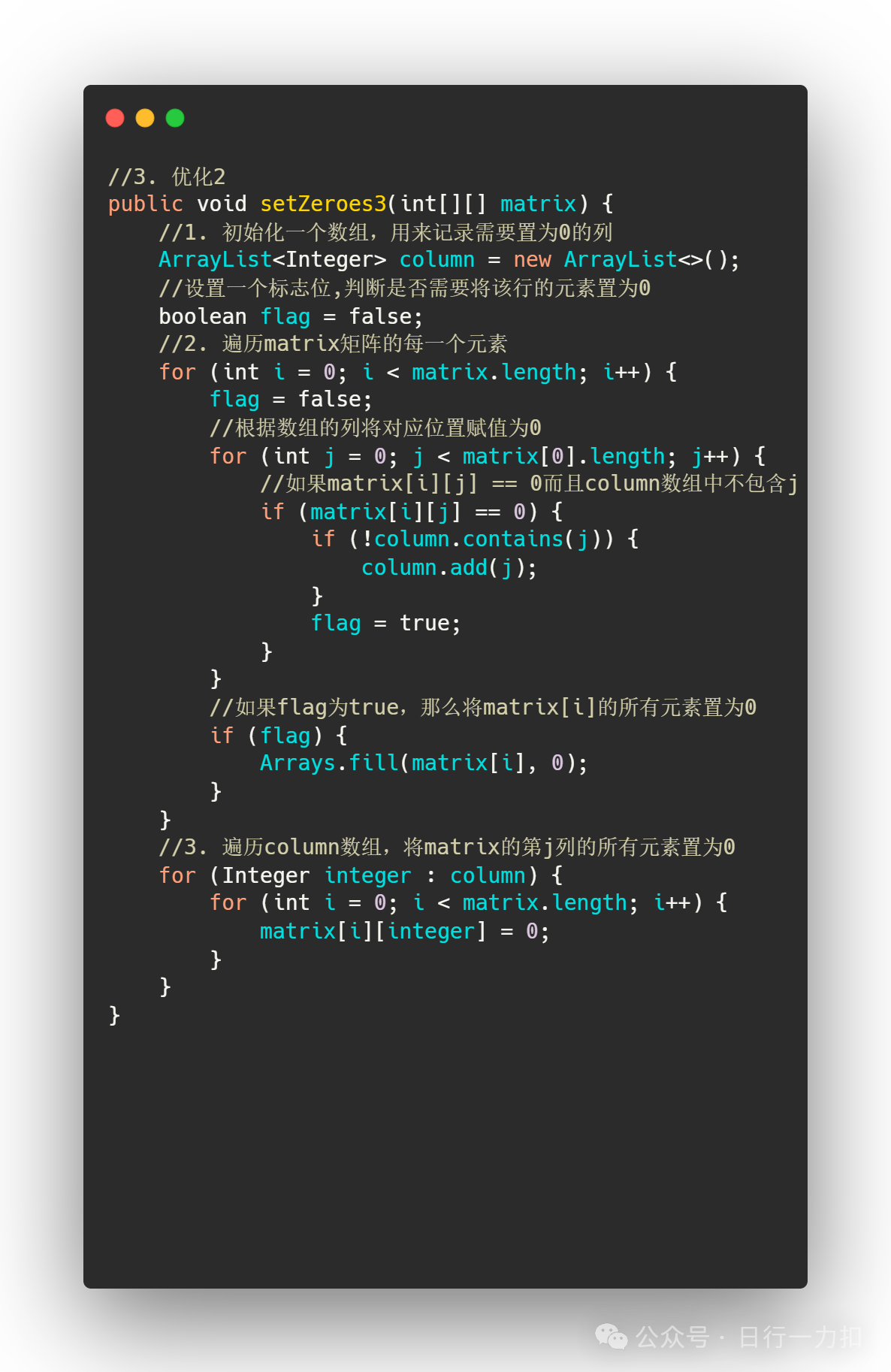
因此我们是不是可以直接不存储那个元素为0,我们只需要一行行遍历矩阵,发现某个元素为0,记录下它所在的列,等到改行遍历完毕,回过头把该行置为0(如果改行有0元素)。在遍历后续行的时候,我们就可以根据前面发现值为0的列将对应位置直接置为0。
代码思路:
-
初始化一个数组,用来记录需要置为0的列
-
遍历矩阵的第一行,发现值为0的元素,就将列值加入数组(如果数组不包含该列的话),然后再将该行所有元素赋值为0
-
如果该行没有值为0的元素,就直接遍历下一行
-
最后遍历column数组,将matrix的第j列的所有元素置为0
这样使用的空间:使用 ArrayList 来存储需要置0的列索引:O(N),在最坏的情况下,如果矩阵的每一列都至少有一个0,则需要存储所有列的索引。
2.4 思路四——优化3
这是我看官方的解析,官方很巧妙的将矩阵的第一行与第一列当作判定数组。其实本质上就和前面的思路2一样,采用两个数组,来表示哪一行需要置为0,哪一列需要置为0,但是这两个数组是用的矩阵原始的第一行与第一列。我将代码加了注释,所以直接读代码应该很清晰:
-
同时需要注意,有些人会问如果第一行或者第一列根本没有0,那你再用它当标志位,之前的值怎么办?
-
所以我需要解释一下:之所以使用第一行与第一列无需再存储它之前的值是因为我们仅仅修改在发现当前行者当前列为0的地方,也就是其它位置我是不动的,如下:
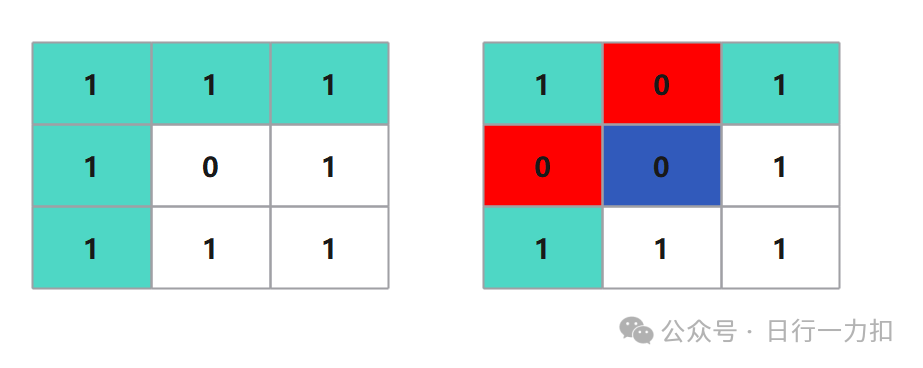
-
当我发现蓝色位置为0,我只更改红色位置的值,这些位置即使第一行与第一列没有0,也是需要更改的。而在结束时如果根据两个判定变量发现第一行与第一列本来没有0,就不需要在做更改了,因为根本没有更改不需要更改的部分。

可以看出这种方法效率还是很高的。
2.5 思路五——优化4
按照上面的官方解析,那就再把思路三种的ArrayList放在矩阵第一行,那也可以使用更少的空间。说做就做,在看了思路三的基础上直接看下面的代码吧


2.6 思路六——优化5——只使用一个变量
在思路五的基础上,我们的判断当前行是否需要置为0的flag是可以省略掉的,如下:
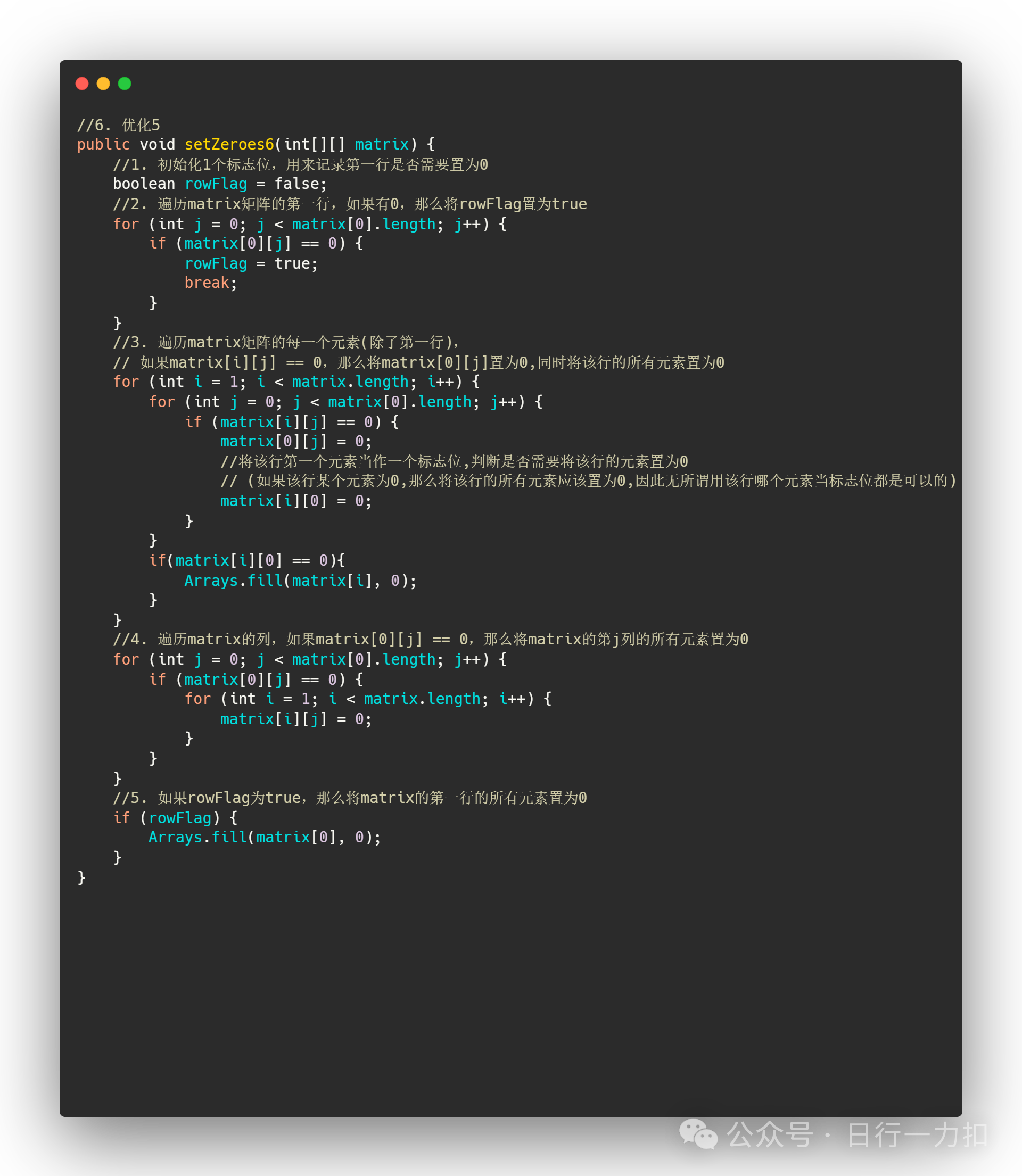
注意这一行:
将该行第一个元素当作一个标志位,判断是否需要将该行的元素置为0
(如果该行某个元素为0,那么将该行的所有元素应该置为0,因此无所谓用该行哪个元素当标志位都是可以的)
按照这种思路只需要使用一个布尔变量就可以完成任务,还是很巧妙的。
3. 代码实现
3.1 思路一

3.2 思路二

3.3 思路三
思路四五六见上
4. 相关复杂度分析
1. 暴力求解
-
时间复杂度: (O(M^2N + MN^2))。因为对于矩阵中的每一个元素,都可能需要遍历整行和整列来将它们置为0。
解释:
-
空间复杂度: (O(MN))。需要一个同样大小的矩阵来存储副本。
2. 优化
-
时间复杂度: (O(MN))。首先遍历一遍矩阵来标记需要置0的行和列,然后根据这些标记来置0,每个步骤都是线性的。
-
空间复杂度: (O(M + N))。使用两个额外的数组来记录需要置0的行和列。
3. 优化2
-
时间复杂度: (O(MN^2))。最坏情况下,对于矩阵的每一个元素,都可能需要遍历整个列索引列表来检查是否已经记录了该列。
-
空间复杂度: (O(N))。使用一个ArrayList来记录需要置0的列。
4. 优化3
-
时间复杂度: (O(MN))。遍历整个矩阵两次,一次用于标记,一次用于实际置0操作。
-
空间复杂度: (O(1))。利用矩阵的第一行和第一列来记录0的位置,除了两个额外的标志位以外不需要其他额外空间。
5. 优化4
-
时间复杂度: (O(MN))。虽然有多次遍历,但每次遍历都是线性的,关键操作还是依赖于矩阵的总元素数量。
-
空间复杂度: (O(1))。仅使用一个额外的标志位来记录第一行是否需要置0,直接在原矩阵上操作。
6. 优化5
-
时间复杂度: (O(MN))。和前一种方法类似,遍历矩阵来标记0的位置,然后根据这些标记来置0。
-
空间复杂度: (O(1))。使用矩阵的第一行和第一个元素来记录行和列是否需要置0,没有使用其他额外空间。
但显然,随着优化的进行,我们尽量减少了空间复杂度,直至达到常数空间复杂度的解法,同时保持了时间复杂度为线性。总之来说还是很有意思的。
相关文章:

面试经典150题——矩阵置零
"Dream it. Wish it. Do it." - Unknown 1. 题目描述 2. 题目分析与解析 2.1 思路一——暴力求解 思路一很简单,就是尝试遍历矩阵的所有元素,如果发现值等于0,就把当前行与当前列的值分别置为0。同时我们需要注意,…...

多端开发围炉夜话
文章目录 一、多端开发 一、多端开发 uni-app 官网 UNI-APP中的UI框架:介绍常用的UI框架及其特点 uView UIVant WeappColor UIMint UI uniapp嵌入android原生开发的功能 uniapp使用安卓原生sdk uni-app中的uni.requireNativePlugin...

分治算法总结(Java)
目录 分治算法概述 快速排序 练习1:排序数组 练习2:数组中的第K个最大元素 练习3:最小k个数 归并排序 练习4:排序数组 练习5:交易逆序对的总数 练习6:计算右侧小于当前元素的个数 练习7࿱…...
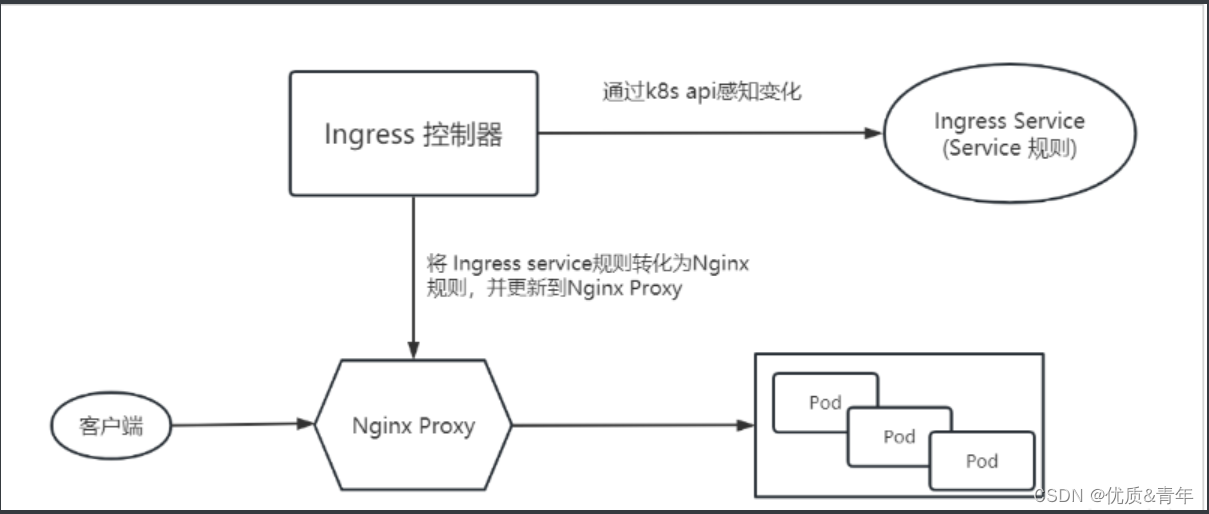
【云原生系列之kubernetes】--Ingress使用
service的缺点: 不支持基于URL等机制对HTTP/HTTPS协议进行高级路由、超时、重试、基于流量的灰度等高级流量治理机制难以将多个service流量统一管理 1.1ingress的概念 ingress是k8s中的一个对象,作用是如何将请求转发到service的规则ingress controlle…...

练习:鼠标类设计之2_类和接口
前言 续鼠标类设计之1,前面解决了鼠标信号问题,这里解决显示问题 引入 鼠标伴随操作系统而生,考虑在屏幕上怎样显示 思路 1>鼠标显示是一个动态效果,所以需要一个“动态效果类”对象,添加进鼠标类的属性里。 在面…...
【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson 15 At the Department Store 在百货商店
《美语从头学初级入门篇》 注意:被 删除线 划掉的不一定不正确,只是不是标准答案。 文章目录 Lesson 15 At the Department Store 在百货商店会话A会话B笔记 Lesson 15 At the Department Store 在百货商店 会话A A: Can you help me, please? B: Sur…...
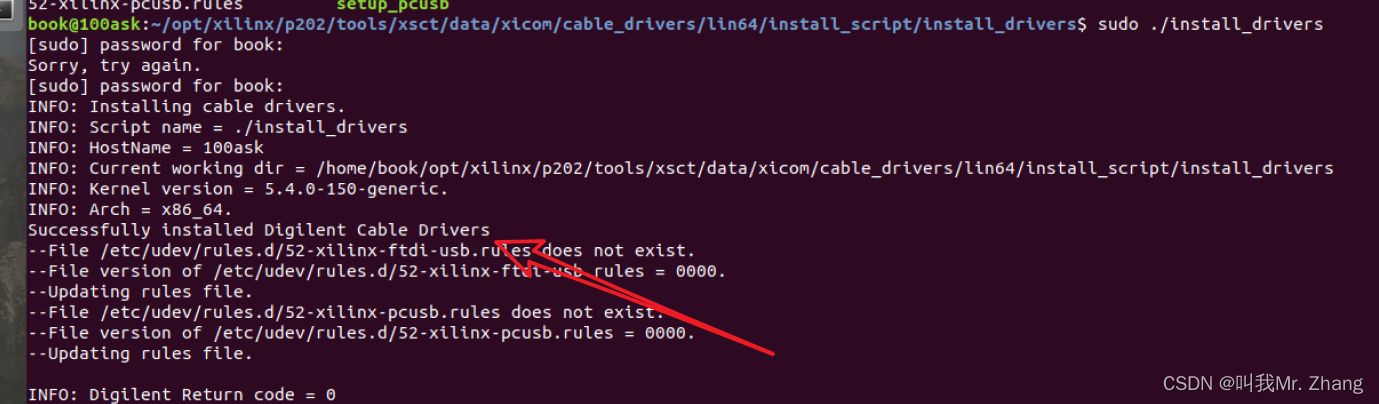
linux 安装、删除 JTAG驱动
安装 安装驱动需要sudo访问权限,所以得手动安装。 在petalinux安装目录下: 文件的路径。 cd tools/xsct/data/xicom/cable_drivers/lin64/install_script/install_drivers 然后执行文件 install_drivers。 sudo ./install_drivers安装成功。 删除 …...
)
CSS的伪类选择器:nth-child()
CSS的伪类选择器:nth-child() CSS的伪类选择器 :nth-child() 是一个非常强大的工具,它允许你根据元素在其父元素中的位置(序数)来选择特定的子元素。这个选择器可以应用于任何元素,并且可以与类型选择器、类选择器或ID选择器结合…...

python celery使用队列
在celery的配置方法中有个参数叫task_routes,是用来设置不同的任务 消费不同的队列(也就是路由)。 格式如下: { ‘task name’: { ‘queue’: ‘queue name’ }}直接上代码,简单明了,目录格式如下&#x…...

四非保研之旅
大家好,我是工藤学编程,虽有万分感概,但是话不多说,先直接进入正题,抒情环节最后再说,哈哈哈 写在开头 我的分享是来给大家涨信心的,网上的大佬们都太强了,大家拿我涨涨信心&#…...
基于Java+SpringBoot的旅游路线规划系统(源码+论文)
文章目录 目录 文章目录 前言 一、功能设计 二、功能实现 1.1 前端首页模块的实现 1.2 景点新闻 1.3 景点在线预订 1.4 酒店在线预订 1.5 管理员景点管理 1.6 管理员旅游线路管理 1.7 酒店信息管理 三、库表设计 前言 随着我国的经济的不断发展,现在的一些热门的景…...

AI与测试自动化:未来已来
AI与测试自动化注定融合。软件开发的速度和准确性要求已经远远超出了预期。测试自动化通过重复、详细和数据密集型测试来解决这个问题,确保敏捷和持续交付环境中的软件质量。AI的学习、适应和预测能力以完美的效率和准确性增强了测试自动化。复杂的算法现在充当质量…...
—张量》)
深度学习基础之《TensorFlow框架(6)—张量》
一、张量 1、什么是张量 张量Tensor和ndarray是有联系的,当我们print()打印值的时候,它返回的就是ndarray对象 TensorFlow的张量就是一个n维数组,类型为tf.Tensor。Tensor具有以下两个重要的属性: (1)typ…...

第三百六十六回
文章目录 1. 概念介绍2. 使用方法2.1 List2.2 Map2.3 Set 3. 示例代码4. 内容总结 我们在上一章回中介绍了"convert包"相关的内容,本章回中将介绍collection.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章回中介绍的内容是col…...
Fiddler工具 — 18.Fiddler抓包HTTPS请求(一)
1、Fiddler抓取HTTPS过程 第一步:Fiddler截获客户端发送给服务器的HTTPS请求,Fiddler伪装成客户端向服务器发送请求进行握手 。 第二步:服务器发回相应,Fiddler获取到服务器的CA证书, 用根证书(这里的根证…...

多租户数据库的缓冲区共享和预分配方案设计
多租户数据库的缓冲区共享和预分配方案设计 文章目录 多租户数据库的缓冲区共享和预分配方案设计简介初始化输入交互输出输入部分的输出交互部分的输出 评分注意点语言要求需要使用的模块系统框架图方案设计初始化阶段交互阶段 修改进度规划最终代码 简介 云计算技术使企业能够…...
C++:C++入门基础
创作不易,感谢三连 !! 一、什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机ÿ…...

利用System.Web.HttpRuntime.Cache制作缓存工具类
用到的依赖介绍 当谈到 ASP.NET 中的缓存管理时,常涉及到以下三个类:CacheDependency、HttpRuntime.Cache 和 System.Web.Caching。 CacheDependency(缓存依赖项): CacheDependency 类用于指定一个或多个文件或目录作…...
)
266.【华为OD机试真题】抢7游戏(深度优先搜索DFS-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-抢7游戏二.解题思路三.题解代码Python题解代码…...
工具分享:在线键盘测试工具
在数字化时代,键盘作为我们与计算机交互的重要媒介之一,其性能和稳定性直接影响到我们的工作效率和使用体验。为了确保键盘的每个按键都能正常工作,并帮助用户检测潜在的延迟、连点等问题,一款优质的在线键盘测试工具显得尤为重要…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
