分治算法总结(Java)
目录
分治算法概述
快速排序
练习1:排序数组
练习2:数组中的第K个最大元素
练习3:最小k个数
归并排序
练习4:排序数组
练习5:交易逆序对的总数
练习6:计算右侧小于当前元素的个数
练习7:翻转对
分治算法概述
分治:即 分而治之。也就是将一个大的问题拆分为若干个小问题,然后递归解决每个小问题,最终合并每个小问题的解得到原问题的解
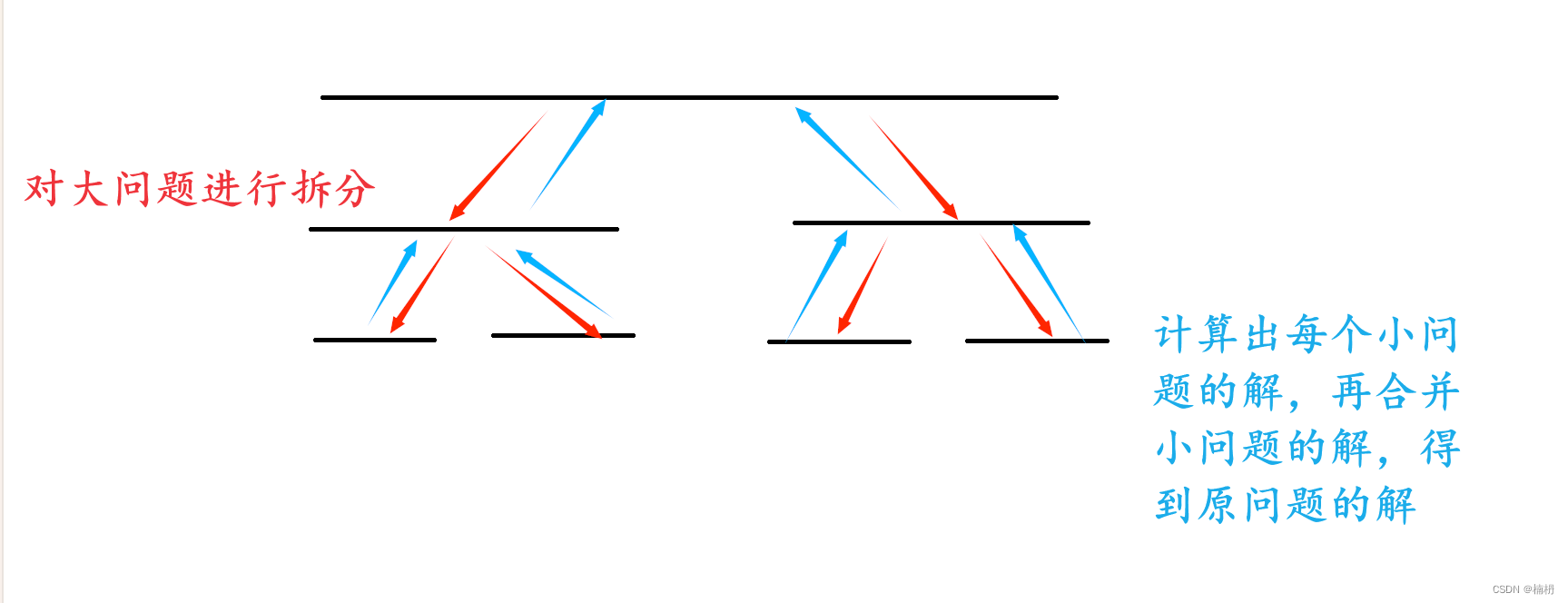
分治算法一般包含 三步:
1. 分割问题:将原问题分割为若干子问题,这些子问题应该是相互独立的,并且和原问题具有相同的结构。
2. 解决子问题:递归解决每个子问题,当子问题足够小时,直接求解
3. 合并子问题的解:将子问题的解合并成原问题的解。
分治的思想体现在 快速排序、归并、二分查找等 中,在本篇文章中,我们重点讲解其在 快速排序和 归并 中的使用。
快速排序
快速排序:用于对数组进行排序,其基本思想是选择一个基准元素,通过将数组中的其他元素按照 与基准元素的大小关系 分为两个(或三个)子数组,然后递归地对这两个(或三个)子数组进行排序,最终将整个数组排序完成。
在分割数组时,可以将数组中的其他元素按照与基准元素的大小关系分为两个子数组,一个子数组中的元素都小于基准元素,另一个子数组中的元素都大于等于基准元素。也可以分为三个子数组,其中,一个子数组中的元素都小于基准元素,一个子数组中的元素都等于基准元素,一个子数组中的元素都大于基准元素。

当将数组分为三块时,等于key区间内的元素已经有序,因此,只需递归排序左边部分和右边部分。当数据中有很多重复数据时,排序效率会大大提升
接下来,我们以一些练习来进一步掌握快速排序
练习1:排序数组
题目链接:
912. 排序数组 - 力扣(LeetCode)
题目描述:
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
思路分析:
在这里,我们使用 快速排序 来对数组进行排序,具体实现步骤为:
1. 选择基准元素:从数组中选择一个元素作为基准元素
那么,该如何选择基准元素呢?
我们可以选择第一个元素作为基准元素,也可以取中间元素作为基准元素,还可以比较第一个元素、中间元素和最后一个元素的大小,选择中间大小的元素作为基准元素。但,从数组中选择元素,我们应该做到随机选择一个元素,因此,我们可以使用随机数来选择基准元素。
2. 分割数组:在这里我们将数组分为三个子数组,其中元素分别为:小于基准元素、等于基准元素和大于基准元素
如何将当前数组中的元素划分为三个部分?
我们可以利用双指针的思想来进行划分,但仅仅使用两个指针无法完成三部分的划分,在这里,要使用三个指针。分别定义left和right,再定义变量i来遍历数组,因此这三个变量将数组划分为四个区间:

i扫描到的元素可能有三种情况:
1. 小于key:此时需要将其放入[l, left]区间内,因此需要将当前元素和left+1位置元素交换,再将left向后移动一位,即可将其放入[l, left]区间内。由于left+1位置元素是等于key的元素,将其交换到i位置后,left + 2到i位置的元素都等于key,此时即可将left向右移动一位,i也可以向右移动一位,继续扫描下一个元素

2. 等于key:此时需要将其放入[left + 1, i]区间内,因此只需将 i 向后移动一位(i++),即可将其放入[left + 1, i]区间内
3. 大于key:此时需要将其放入[right, r]区间内,因此需要将当前元素与right -1位置元素进行交换,此时再将right - 1,即可将其放入[right, r]区间内,但由于[i, right-1]区间内的元素是未排序元素,因此,不能移动i,要继续判断此时i位置上元素与key的大小关系
当i等于right时,此时数组被划分为三个区间,循环结束
3. 递归排序:由于等于基准元素的子数组已经有序,因此,我们只需对 小于基准元素 和 大于基准元素的子数组 分别递归应用快速排序算法,直到子数组的长度为1或者0,此时子数组已经有序。
4. 合并结果:将排序好的子数组合并,即可得到整个数组的有序序列。
代码实现:
class Solution {public int[] sortArray(int[] nums) {sort(nums, 0, nums.length - 1);return nums;}private void sort(int[] nums, int l, int r){if(l >= r) return;//递归结束int key = nums[new Random().nextInt(r - l + 1) + l];//利用随机数来选择基准元素//将数组分为三块int left = l - 1, right = r + 1, i = l;while(i < right){//注意:条件为 i < right,而不是i < nums.lengthif(nums[i] < key) swap(nums, ++left, i++);else if(nums[i] == key) i++;else swap(nums, --right, i);}//继续递归排序左区间和右区间sort(nums, l, left);sort(nums, right, r);}private void swap(int[] nums, int a, int b){int temp = nums[a];nums[a] = nums[b];nums[b] = temp;}
}练习2:数组中的第K个最大元素
题目链接:
215. 数组中的第K个最大元素 - 力扣(LeetCode)
题目描述:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
思路分析:
要求数组中第K个最大的元素,我们可以想到使用堆排序,建立 大小为k 的小根堆,遍历数组,若当前元素大于堆顶元素,就将堆顶元素弹出,再将该元素放入堆中,遍历完后,小根堆堆顶元素即为第K个最大的元素
堆排序代码实现:
class Solution {public int findKthLargest(int[] nums, int k) {//建立小根堆PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o1 - o2;}});for (int i = 0; i < nums.length; i++) {if(priorityQueue.size() < k){//当小根堆未满时,直接向其中添加元素priorityQueue.add(nums[i]);}else {//当小根堆满时,需判断是否需要更新元素if(priorityQueue.peek() < nums[i]){//若当前元素大于堆顶元素,弹出堆顶元素,放入当前元素priorityQueue.poll();priorityQueue.add(nums[i]);}}}return priorityQueue.peek();}
}我们也可以使用 快速排序 来找到数组中第K个最大的元素:
我们首先通过基准元素key将数组划分为三块,设三个区间内的元素个数分别为a b c

再判断第k个最大的数落在哪个区间内
由于要找的是最大的第K个数,因此,我们先判断右侧(包含较大数)的区间,再判断中间和左边
若k <= c:此时第K个最大的元素落在[right, r]区间内,我们需要继续在[right, r] 区间内找第K个最大的元素
若 k > c 且 k >= c + b,此时第K个最大的元素落在[left + 1, right - 1]区间内,即第k个最大的元素为基准元素key,直接返回即可
若k <= a,此时第K个最大的元素落在[l, left]区间内,我们需要继续在[l, left] 区间内找,但此时,我们要在[l, left]区间内找的是:第 k - a - b个最大的元素,即直接排除大于key和等于key的所有元素
代码实现:
class Solution {public int findKthLargest(int[] nums, int k) {return sort(nums, 0, nums.length - 1, k);}private int sort(int[] nums, int l, int r, int k){if(l >= r) return nums[l];//递归结束//随机选择基准元素int key = nums[new Random().nextInt(r - l + 1) + l];//将数组划分为三块int left = l - 1, right = r + 1, i = l;while(i < right){if(nums[i] < key) swap(nums, ++left, i++);else if(nums[i] == key) i++;else swap(nums, --right, i);}//判断第k个最大的元素在哪个区间int c = r - right + 1, b = right - left - 1;if(c >= k) return sort(nums, right, r, k);//在右区间继续寻找第k个最大的元素else if(c + b >= k) return key;//第k个最大的元素为k,直接返回else return sort(nums, l, left, k - b - c);//在左区间继续寻找}private void swap(int[] nums, int a, int b){int temp = nums[a];nums[a] = nums[b];nums[b] = temp;}
}练习3:最小k个数
题目链接:
面试题 17.14. 最小K个数 - 力扣(LeetCode)
题目描述:
设计一个算法,找出数组中最小的k个数。以任意顺序返回这k个数均可。
示例:
输入: arr = [1,3,5,7,2,4,6,8], k = 4 输出: [1,2,3,4]
提示:
0 <= len(arr) <= 1000000 <= k <= min(100000, len(arr))
思路分析:
同样的,这道题也可以利用 大根堆 来找到 最小的k个数
堆排序代码实现:
class Solution {public int[] smallestK(int[] arr, int k) {int[] ret = new int[k];//判断特殊情况if(arr.length <= 0 || k <= 0) return ret;//建立大根堆PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});for (int i = 0; i < arr.length; i++) {if(priorityQueue.size() < k){//当大根堆未满时,直接向其中添加元素priorityQueue.add(arr[i]);}else {//当大根堆满时,需判断是否需要更新元素if(priorityQueue.peek() > arr[i]){//若当前元素小于堆顶元素,弹出堆顶元素,放入当前元素priorityQueue.poll();priorityQueue.add(arr[i]);}}}for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}
}由于可以以 任意顺序 返回这k个数,因此,我们也可以利用 快速排序 来找到这最小的k个数,本题的解题思路与练习2类似,唯一不同的是:本题需要返回一个大小为k的数组
因此,我们创建一个大小为k的数组ret
同样的,通过基准元素key将数组划分为三块,设三个区间内的元素个数分别为a b c
接下来,在判断这k个数在哪个区间内:
由于我们要找的是最小的k个数,因此我们先判断左边(较小元素所在区间),再判断中间和右边
若 k < a,则最小的k个数都在小于key的区间内,因此我们继续在[l, left]区间内找最小k个数
若k >= a 且 k <= a + b,则最小的k个数包含[l, left]区间所有元素 和部分 [left + 1, right - 1]区间内元素,因此,我们只需将这k个元素放入ret中,就找到了最小k个数
若k > a + b,此时最小的k个数包含[l, right - 1]区间内所有元素,因此,我们先将这 a + b个元素放入ret中,再在[right, r]中找剩下k - a - b个数
由于经过快排后,数组中前k个元素就是最小的k个数,因此我们可以在快速排序结束后,将这k个数放入ret中并返回
代码实现:
class Solution {public int[] smallestK(int[] arr, int k) {findsmall(arr, 0, arr.length - 1, k);int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = arr[i];}return ret;}private void findsmall(int[] arr, int l, int r, int k){if(l >= r) return;//递归结束//随机选择基准元素int key = arr[new Random().nextInt(r - l + 1) + l];//数组分三块int left = l - 1, right = r + 1, i = l;while(i < right){if(arr[i] < key){swap(arr, ++left, i++);}else if(arr[i] == key){i++;}else {swap(arr, --right, i);}}//分情况讨论int a = left - l + 1, b = right - left - 1;if(k < a) findsmall(arr, l, left, k);else if(k <= a + b) return;else findsmall(arr, right, r, k - a - b);}private void swap(int[] nums, int i, int j){int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}
}归并排序
归并排序:用于对一个数组进行排序。它的基本思想是将数组划分为两个子数组,递归地对这两个子数组进行排序,最终将两个有序的子数组合并成一个有序的数组。
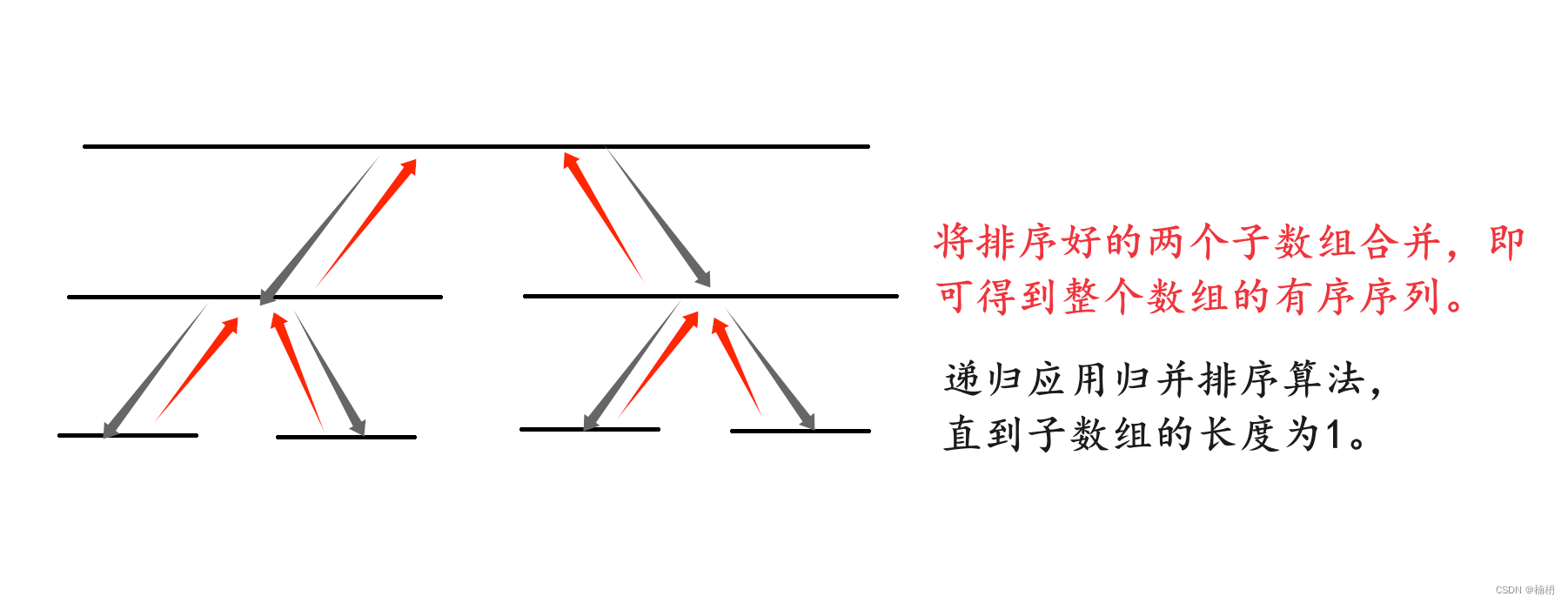
归并排序的解题步骤为:
1. 分割数组:将数组平均分成两个子数组,直到每个子数组只包含一个元素。
2. 递归排序:对两个子数组分别递归地应用归并排序算法,直到子数组的长度为1。
3. 合并结果::将排序好的两个子数组合并,即可得到整个数组的有序序列。在合并时,可使用双指针或额外数组来完成合并
接下来,我们以几道练习来进一步掌握归并排序
练习4:排序数组
题目链接:
912. 排序数组 - 力扣(LeetCode)
题目描述:
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 104-5 * 104 <= nums[i] <= 5 * 104
思路分析:
在这里,我们使用 归并排序 来解决本题。
首先我们进行拆分:将数组一分为二分为两部分,直到分解到数组的长度为1,使整个数组的排序过程被分为 左半部分排序 + 右半部分排序
接下来我们进行合并:将两个较短的有序数组合并成一个长的有序数组,一直合并到最初的长度
如何合并两个较短的有序数组?
我们可以使用一个新的数组保存临时结果,再使用两个指针分别指向两个较短数组的起始位置,然后判断两指针所指元素大小,谁小就将其放入临时数组中,再向后移动,这样,就将合并结果放入临时数组中,然后再将临时数组中的元素放入原数组中,即可合并两个有序数组

代码实现:
class Solution {int[] temp;//为了节省额外的空间开销,我们将临时数组定义为成员变量public int[] sortArray(int[] nums) {temp = new int[nums.length];mergerSort(nums, 0, nums.length - 1);return nums;}private void mergerSort(int[] nums, int left, int right){if(left >= right) return;//只有一个元素时,递归结束int mid = (left + right) / 2;//以中间元素划分左右区间mergerSort(nums, left, mid);//继续递归,将左右子区间排好序mergerSort(nums, mid + 1, right);int cur1 = left, cur2 = mid + 1, i = left;//合并两个有序数组while(cur1 <= mid && cur2 <= right){temp[i++] = nums[cur1] <= nums[cur2] ? nums[cur1++] : nums[cur2++];}//将未变量完的数组元素放入temp中while(cur1 <= mid) temp[i++] = nums[cur1++];while(cur2 <= right) temp[i++] = nums[cur2++];//将temp中数据更新到nums中for(int j = left; j <= right; j++){nums[j] = temp[j];}}
}练习5:交易逆序对的总数
题目链接:
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
题目描述:
在股票交易中,如果前一天的股价高于后一天的股价,则可以认为存在一个「交易逆序对」。请设计一个程序,输入一段时间内的股票交易记录 record,返回其中存在的「交易逆序对」总数。
示例 1:
输入:record = [9, 7, 5, 4, 6] 输出:8 解释:交易中的逆序对为 (9, 7), (9, 5), (9, 4), (9, 6), (7, 5), (7, 4), (7, 6), (5, 4)。
限制:
0 <= record.length <= 50000
思路分析:
首先我们可以想到暴力枚举,即计算每个数的逆序对,再相加,即可求出总的逆序对的个数。但其时间复制度为O(n^2),很有可能超出时间限制。接下来,我们考虑能否使用归并排序来解决该问题,我们可以利用归并排序中 两个较短的有序数组 来快速统计出逆序对的个数
若有序数组为升序:
由于要前一个元素大于后一个元素才能构成逆序对(a, b)且此时数组为升序,因此,我们可以以右半部分元素b为基准,找到左半部分所有大于当前元素a的元素。当左半部分第一次出现比b大的元素a时,说明左半部分中 当前元素 到 右边界的元素 都比b大,此时就可直接计算出b可以构成的逆序对,此时右半部分的指针再向后移动一位到元素c,左半部分的指针也不必回退到起始位置(由于a前面的元素都比b小,不能构成逆序对,c >= b,则a前面的元素也不可能和c构成逆序对)

即:nums[cur1] > nums[cur2] ret(逆序对总数) += (mid - cur1 + 1), cur2++
nums[cur1] <= nums[cur2] cur1++
能否以左半部分元素a为基准呢?
若以左半部分元素a为基准,我们需要在右半部分找到所有小于a的元素, 此时,当第一次出现大于或等于a的元素b,说明 b 到右边界 right 的所有元素均不能构成逆序对,因此小于a的元素为 mid+1 到 当前元素位置 - 1的所有元素,
即:nums[cur2] >= nums[cur1] ret += cur2 - (mid + 1) cur1++
nums[cur2] < nums[cur1] cur2++
但,若右半部分区域没有大于或等于a的元素b,此时cur2直接移动到最右端,此时退出循环,未统计所有逆序对,因此,若要使用这种方法,还需要判断边界情况,较为复杂,因此不推荐使用
若有序数组为降序:
同样的,由于要前一个元素大于后一个元素才能构成逆序对(a, b),且此时有序数组为降序,因此,我们以左半部分元素a为基准,找到右半部分中比a小的所有元素。当右半部分第一次出现小于a的元素b,则 右半部分当前元素cur2 到 右边界right 的所有元素都小于a,则可求出a能构成的逆序对。
因此:nums[cur2] < nums[cur1] ret(逆序对总数) += (right - cur2 + 1), cur1++
nums[cur2] >= nums[cur1] cur2++
代码实现:
升序:
class Solution {int[] temp;public int reversePairs(int[] record) {temp = new int[record.length];return mergerSort(record, 0, record.length - 1);}private int mergerSort(int[] nums, int left, int right){if(left >= right) return 0;//当只有一个元素或没有元素时,递归结束,此时无逆序对,返回0int mid = (left + right) / 2;int ret = 0;//计算总的逆序对个数//递归,求左半部分逆序对的个数 和 右半部分逆序对的个数ret += mergerSort(nums, left, mid);ret += mergerSort(nums, mid + 1, right);//求 左半部分 与 右半部分构成的逆序对,同时进行排序(此时为升序)int cur1 = left, cur2 = mid + 1, i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur1] > nums[cur2]){ret += mid - cur1 + 1;temp[i++] = nums[cur2++];}else{temp[i++] = nums[cur1++];}}//将剩余元素放入temp中while(cur1 <= mid) temp[i++] = nums[cur1++];while(cur2 <= right) temp[i++] = nums[cur2++];//将排序结果更新到nums中for(int j = left; j <= right; j++){nums[j] = temp[j];}return ret;}
}降序:
class Solution {int[] temp;public int reversePairs(int[] record) {temp = new int[record.length];return mergerSort(record, 0, record.length - 1);}private int mergerSort(int[] nums, int left, int right){if(left >= right) return 0;//当只有一个元素或没有元素时,递归结束,此时无逆序对,返回0int mid = (left + right) / 2;int ret = 0;//计算总的逆序对个数//递归,求左半部分逆序对的个数 和 右半部分逆序对的个数ret += mergerSort(nums, left, mid);ret += mergerSort(nums, mid + 1, right);//求 左半部分 与 右半部分构成的逆序对,同时进行排序(此时为降序)int cur1 = left, cur2 = mid + 1, i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur2] < nums[cur1]){ret += right - cur2 + 1;temp[i++] = nums[cur1++];}else{temp[i++] = nums[cur2++];}}//将剩余元素放入temp中while(cur1 <= mid) temp[i++] = nums[cur1++];while(cur2 <= right) temp[i++] = nums[cur2++];//将排序结果更新到nums中for(int j = left; j <= right; j++){nums[j] = temp[j];}return ret;}
}练习6:计算右侧小于当前元素的个数
题目链接:
315. 计算右侧小于当前元素的个数 - 力扣(LeetCode)
题目描述:
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
示例 1:
输入:nums = [5,2,6,1]
输出:[2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1)
2 的右侧仅有 1 个更小的元素 (1)
6 的右侧有 1 个更小的元素 (1)
1 的右侧有 0 个更小的元素
示例 2:
输入:nums = [-1] 输出:[0]
示例 3:
输入:nums = [-1,-1] 输出:[0,0]
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
思路分析:
本题与 练习5 类似,都要求后面的元素小于前面的元素,但不同的是,本题要返回一个新的数组,且数组中存放的是原数组中每个元素右侧小于 nums[i] 的元素数量
那么应该如何处理呢?
归并排序后会打乱数组原有的顺序,因此我们要解决的问题就是 如何找到数组元素原有的位置,在这里我们可以使用一个 下标数组index,来记录每个元素的下标,然后将下标数组 index 和原数组 nums 绑定在一起,一起移动,这样,就算数组重新进行排序,也能够通过下标数组找到元素原位置

此时我们创建一个新的数组ret 保存原nums[i]右侧小于nums[i]的元素数量,在合并两个有序数组时,计算出 nums[k] 的右侧小于当前元素的个数 count 后,利用数组下标找到该元素原有下标:index[k],再将结果更新到数组ret中:ret[index[k]] += count
代码实现:
class Solution {int[] ret;int[] index;//下标数组int[] tempNums;//临时数组int[] tempIndex;//临时下标数组public List<Integer> countSmaller(int[] nums) {int n = nums.length;//数组长度ret = new int[n];index = new int[n];tempNums = new int[n];tempIndex = new int[n]; //初始化下标数组for(int i = 0; i < n; i++){index[i] = i;}//归并排序mergerSort(nums, 0, n - 1);//将结果放入list中List<Integer> list = new ArrayList<>();for(int x: ret) list.add(x);return list;}private void mergerSort(int[] nums, int left, int right){if(left >= right) return;//当只有一个元素或没有元素时,没有小于该元素的元素,直接返回int mid = (left + right) / 2;//根据中间元素将数组划分为两个区间//递归处理左区间和右区间mergerSort(nums, left, mid);mergerSort(nums, mid+1, right);//求左半部分元素 在 右半部分中 有多少个元素比其小//因此我们对数组降序排列int cur1 = left, cur2 = mid + 1, i = left;while(cur1 <= mid && cur2 <= right){if(nums[cur1] > nums[cur2]){ret[index[cur1]] += right - cur2 + 1;//更新当前元素的 右侧小于该元素 的个数tempNums[i] = nums[cur1];//将元素放入临时数组中tempIndex[i++] = index[cur1++];//注意:该元素的下标也要同步进行保存}else{tempNums[i] = nums[cur2];tempIndex[i++] = index[cur2++];}}//将剩余元素放入临时数组中while(cur1 <= mid){tempNums[i] = nums[cur1];tempIndex[i++] = index[cur1++];}while(cur2 <= right){tempNums[i] = nums[cur2];tempIndex[i++] = index[cur2++];}//将数据更新到nums和index中for(int j = left; j <= right; j++){nums[j] = tempNums[j];index[j] = tempIndex[j];}}
}练习7:翻转对
题目链接:
493. 翻转对 - 力扣(LeetCode)
题目描述:
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
示例 1:
输入: [1,3,2,3,1] 输出: 2
示例 2:
输入: [2,4,3,5,1] 输出: 3
注意:
- 给定数组的长度不会超过
50000。 - 输入数组中的所有数字都在32位整数的表示范围内。
思路分析:
本题同样与练习5类似,但此时 nums[i] > 2*nums[j],即要满足当前元素 大于 右侧元素的两倍,或当前元素 小于 左侧元素的一半。在这里仍可以使用 归并排序 来解决该问题,此时我们使用降序排列,以左半部分元素为基准,在右半部分中找 小于该元素的所有元素。由于这里判断的条件为 nums[i] > 2*nums[j],因此,我们不能再 边计算结果边排序(当前元素小于右侧元素的2倍,但不一定小于右侧元素,如:5 < 2*3 但 5 > 3),因此,我们需要先计算翻转对的个数,再进行排序。
代码实现:
class Solution {int[] temp;public int reversePairs(int[] nums) {temp = new int[nums.length];return mergerSort(nums, 0, nums.length - 1);}private int mergerSort(int[] nums, int left, int right){if(left >= right) return 0;//递归结束int mid = (left + right) / 2;//继续递归int ret = 0;ret += mergerSort(nums, left, mid);ret += mergerSort(nums, mid + 1, right);//计算翻转对//当前元素后,有多少个元素的二倍小于当前元素int cur1 = left, cur2 = mid + 1, i = left;while(cur1 <= mid && cur2 <= right){//虽然所有元素的大小都在int类型范围内,但2倍后却有可能溢出,因此要使用long类型if((long)nums[cur1] > (long)2 * nums[cur2]){//也可以判断 当前元素的一半是否大于 右侧元素 nums[cur1] / 2.0 > nums[cur2]ret += (right - cur2 + 1);cur1++;}else{cur2++;}}//降序排序cur1 = left; cur2 = mid+1;while(cur1 <= mid && cur2 <= right){if(nums[cur1] > nums[cur2]){temp[i++] = nums[cur1++];}else{temp[i++] = nums[cur2++];}}//将剩余元素放入temp中while(cur1 <= mid){temp[i++] = nums[cur1++];}while(cur2 <= right){temp[i++] = nums[cur2++];}//将排序后的元素放入nums中for(int j = left; j <= right; j++){nums[j] = temp[j];}return ret;}
}相关文章:

分治算法总结(Java)
目录 分治算法概述 快速排序 练习1:排序数组 练习2:数组中的第K个最大元素 练习3:最小k个数 归并排序 练习4:排序数组 练习5:交易逆序对的总数 练习6:计算右侧小于当前元素的个数 练习7࿱…...
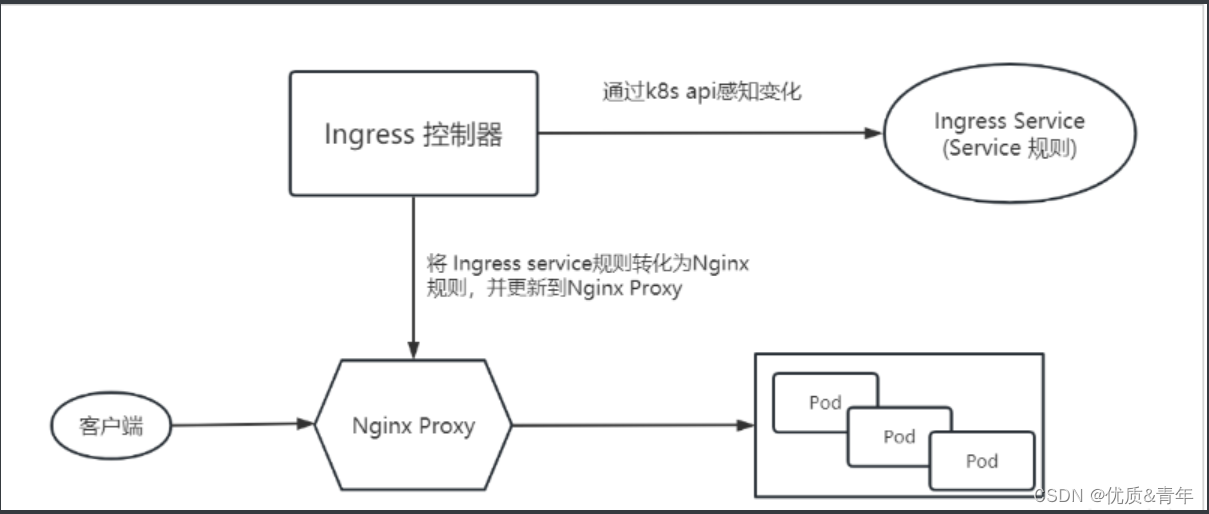
【云原生系列之kubernetes】--Ingress使用
service的缺点: 不支持基于URL等机制对HTTP/HTTPS协议进行高级路由、超时、重试、基于流量的灰度等高级流量治理机制难以将多个service流量统一管理 1.1ingress的概念 ingress是k8s中的一个对象,作用是如何将请求转发到service的规则ingress controlle…...

练习:鼠标类设计之2_类和接口
前言 续鼠标类设计之1,前面解决了鼠标信号问题,这里解决显示问题 引入 鼠标伴随操作系统而生,考虑在屏幕上怎样显示 思路 1>鼠标显示是一个动态效果,所以需要一个“动态效果类”对象,添加进鼠标类的属性里。 在面…...
【程序员英语】【美语从头学】初级篇(入门)(笔记)Lesson 15 At the Department Store 在百货商店
《美语从头学初级入门篇》 注意:被 删除线 划掉的不一定不正确,只是不是标准答案。 文章目录 Lesson 15 At the Department Store 在百货商店会话A会话B笔记 Lesson 15 At the Department Store 在百货商店 会话A A: Can you help me, please? B: Sur…...
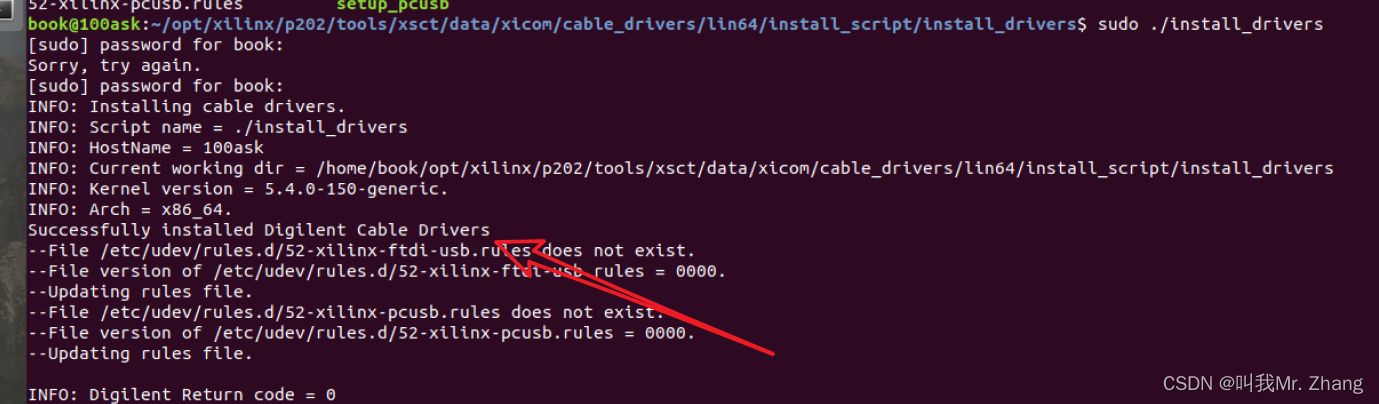
linux 安装、删除 JTAG驱动
安装 安装驱动需要sudo访问权限,所以得手动安装。 在petalinux安装目录下: 文件的路径。 cd tools/xsct/data/xicom/cable_drivers/lin64/install_script/install_drivers 然后执行文件 install_drivers。 sudo ./install_drivers安装成功。 删除 …...
)
CSS的伪类选择器:nth-child()
CSS的伪类选择器:nth-child() CSS的伪类选择器 :nth-child() 是一个非常强大的工具,它允许你根据元素在其父元素中的位置(序数)来选择特定的子元素。这个选择器可以应用于任何元素,并且可以与类型选择器、类选择器或ID选择器结合…...

python celery使用队列
在celery的配置方法中有个参数叫task_routes,是用来设置不同的任务 消费不同的队列(也就是路由)。 格式如下: { ‘task name’: { ‘queue’: ‘queue name’ }}直接上代码,简单明了,目录格式如下&#x…...

四非保研之旅
大家好,我是工藤学编程,虽有万分感概,但是话不多说,先直接进入正题,抒情环节最后再说,哈哈哈 写在开头 我的分享是来给大家涨信心的,网上的大佬们都太强了,大家拿我涨涨信心&#…...
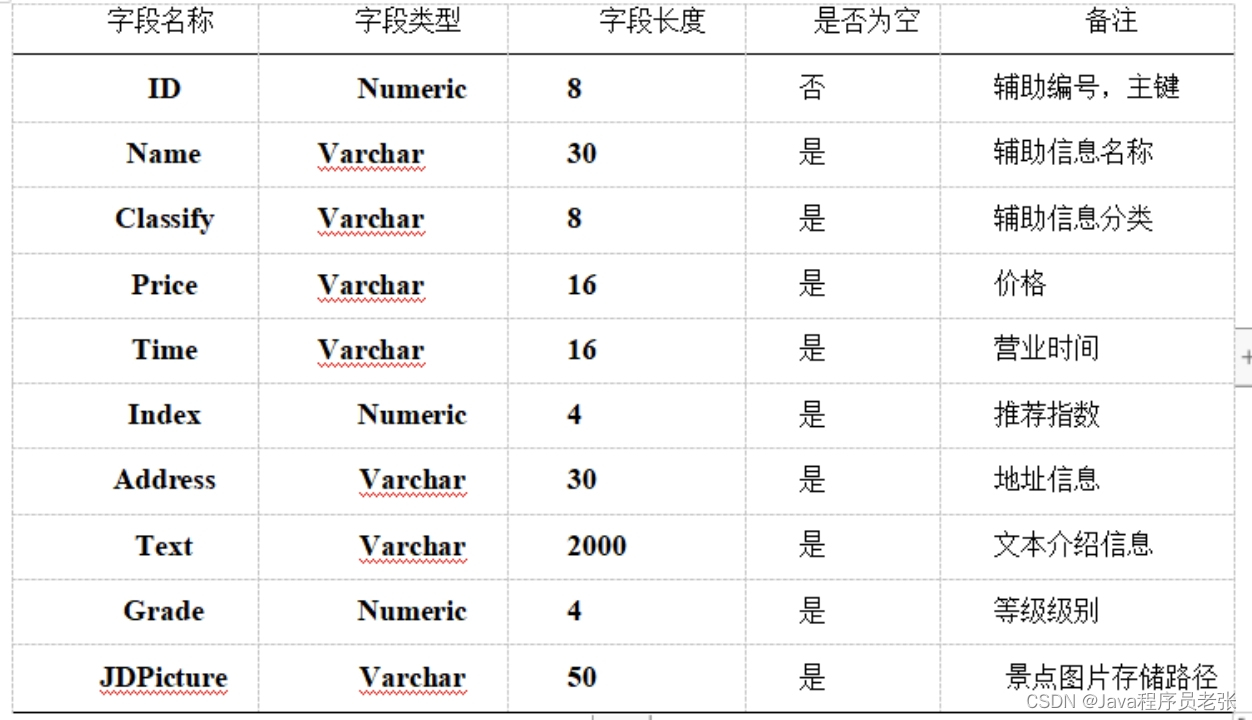
基于Java+SpringBoot的旅游路线规划系统(源码+论文)
文章目录 目录 文章目录 前言 一、功能设计 二、功能实现 1.1 前端首页模块的实现 1.2 景点新闻 1.3 景点在线预订 1.4 酒店在线预订 1.5 管理员景点管理 1.6 管理员旅游线路管理 1.7 酒店信息管理 三、库表设计 前言 随着我国的经济的不断发展,现在的一些热门的景…...

AI与测试自动化:未来已来
AI与测试自动化注定融合。软件开发的速度和准确性要求已经远远超出了预期。测试自动化通过重复、详细和数据密集型测试来解决这个问题,确保敏捷和持续交付环境中的软件质量。AI的学习、适应和预测能力以完美的效率和准确性增强了测试自动化。复杂的算法现在充当质量…...
—张量》)
深度学习基础之《TensorFlow框架(6)—张量》
一、张量 1、什么是张量 张量Tensor和ndarray是有联系的,当我们print()打印值的时候,它返回的就是ndarray对象 TensorFlow的张量就是一个n维数组,类型为tf.Tensor。Tensor具有以下两个重要的属性: (1)typ…...

第三百六十六回
文章目录 1. 概念介绍2. 使用方法2.1 List2.2 Map2.3 Set 3. 示例代码4. 内容总结 我们在上一章回中介绍了"convert包"相关的内容,本章回中将介绍collection.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章回中介绍的内容是col…...
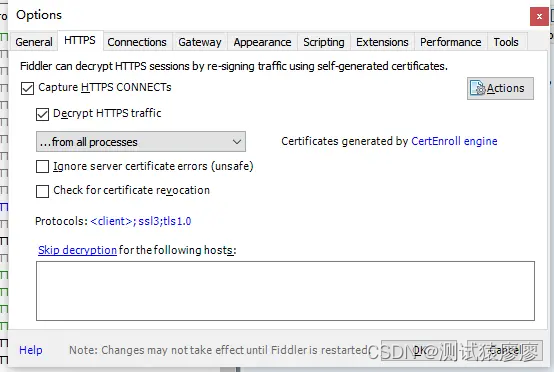
Fiddler工具 — 18.Fiddler抓包HTTPS请求(一)
1、Fiddler抓取HTTPS过程 第一步:Fiddler截获客户端发送给服务器的HTTPS请求,Fiddler伪装成客户端向服务器发送请求进行握手 。 第二步:服务器发回相应,Fiddler获取到服务器的CA证书, 用根证书(这里的根证…...

多租户数据库的缓冲区共享和预分配方案设计
多租户数据库的缓冲区共享和预分配方案设计 文章目录 多租户数据库的缓冲区共享和预分配方案设计简介初始化输入交互输出输入部分的输出交互部分的输出 评分注意点语言要求需要使用的模块系统框架图方案设计初始化阶段交互阶段 修改进度规划最终代码 简介 云计算技术使企业能够…...
C++:C++入门基础
创作不易,感谢三连 !! 一、什么是C C语言是结构化和模块化的语言,适合处理较小规模的程序。对于复杂的问题,规模较大的程序,需要高度的抽象和建模时,C语言则不合适。为了解决软件危机ÿ…...

利用System.Web.HttpRuntime.Cache制作缓存工具类
用到的依赖介绍 当谈到 ASP.NET 中的缓存管理时,常涉及到以下三个类:CacheDependency、HttpRuntime.Cache 和 System.Web.Caching。 CacheDependency(缓存依赖项): CacheDependency 类用于指定一个或多个文件或目录作…...
)
266.【华为OD机试真题】抢7游戏(深度优先搜索DFS-JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-抢7游戏二.解题思路三.题解代码Python题解代码…...
工具分享:在线键盘测试工具
在数字化时代,键盘作为我们与计算机交互的重要媒介之一,其性能和稳定性直接影响到我们的工作效率和使用体验。为了确保键盘的每个按键都能正常工作,并帮助用户检测潜在的延迟、连点等问题,一款优质的在线键盘测试工具显得尤为重要…...
Arcmap excel转shp
使用excel表格转shp的时候,如果你的excel里面有很多字段,直接转很大概率会出现转换结果错误的情况,那么就需要精简一下字段的个数。将原来的表格文件另存一份,在另存为的文件中只保留关键的经度、纬度、和用于匹配的字段即可&…...

14. rk3588自带的RKNNLite检测yolo模型(python)
首先将文件夹~/rknpu2/runtime/RK3588/Linux/librknn_api/aarch64/下的文件librknnrt.so复制到文件夹/usr/lib/下(该文件夹下原有的文件librknnrt.so是用来测试resnet50模型的,所以要替换成yolo模型的librknnrt.so),如下图所示&am…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
