【LeetCode】509. 斐波那契数(简单)——代码随想录算法训练营Day38
题目链接:509. 斐波那契数
题目描述
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
文章讲解:代码随想录
视频讲解:手把手带你入门动态规划 | LeetCode:509.斐波那契数_哔哩哔哩_bilibili
题解1:动态规划
思路:使用动态规划的思路来求解本题,学习动态规划的基本思路。
动态规划分析:
- dp 数组以及下标的含义:dp[i] 为第 i 个斐波那契数。
- 递推公式:dp[i] = dp[i - 1] + dp[i - 2]。
- dp 数组初始化:dp[0] = 0,dp[1] = 1。
- 遍历顺序:从前向后。
- 打印 dp 数组:0、1、1、2、3、......
/*** @param {number} n* @return {number}*/
var fib = function(n) {const dp = new Array(n + 1);dp[0] = 0;dp[1] = 1;for (let i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
};分析:时间复杂度为 O(n),空间复杂度为 O(n)。
题解2:动态规划优化
思路:可以看到 dp[i] 依赖于前2个状态,用2个变量记录前2个数,在循环中直接更新这2个变量。
/*** @param {number} n* @return {number}*/
var fib = function(n) {if (n === 0) {return 0;}if (n <= 2) {return 1;}let a = 1, b = 1;while (n-- > 2) {const c = a + b;a = b;b = c;}return b;
};分析:时间复杂度为 O(n),空间复杂度为 O(1)。
收获
动态规划5步曲:
- dp 数组以及下标的含义。
- 递推公式。
- dp 数组初始化。
- 遍历顺序。
- 打印 dp 数组。
相关文章:
——代码随想录算法训练营Day38)
【LeetCode】509. 斐波那契数(简单)——代码随想录算法训练营Day38
题目链接:509. 斐波那契数 题目描述 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n -…...
 函数对累积缓存设置)
[OpenGL教程05 ] glAccum() 函数对累积缓存设置
Accumulation Buffer:累积缓存 一、说明 openGL编程之所以困难,是因为它是三维图表示;简简单单加入一个Z轴,却使得几何遮挡、光线过度、运动随影等搞得尤其复杂。它的核心处理环节是像素缓存,本篇的积累缓存就是其一个…...

BeautifulSoup的使用与入门
1. 介绍 BeautifulSoup是用来从HTML、XML文档中提取数据的一个python库,安装如下: pip install beautifulsoup4 它支持多种解析器,包括python标准库、lxml HTML解析器、lxml XML解析器、html5lib等。结合稳定性和速度,这里推荐使用lxml HT…...
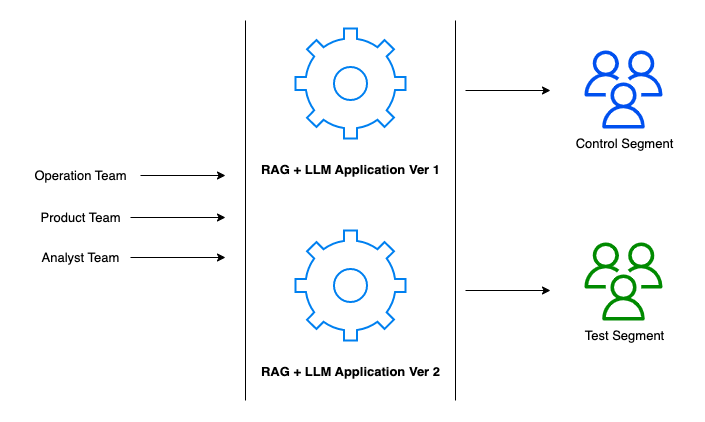
LLM之RAG实战(二十七)| 如何评估RAG系统
有没有想过今天的一些应用程序是如何看起来几乎神奇地智能的?这种魔力很大一部分来自于一种叫做RAG和LLM的东西。把RAG(Retrieval Augmented Generation)想象成人工智能世界里聪明的书呆子,它会挖掘大量信息,准确地找到…...

Linux Docker 关闭开机启动
说说自己为什么需要关闭自启动:Linux中安装Docker后,自启动会占用80和443端口,然后使用自己的SSL认证,导致自己Nginx配置的SSL认证失效,网站通过https打开显示不安全。 Docker是一个容器化平台,它可以让开…...
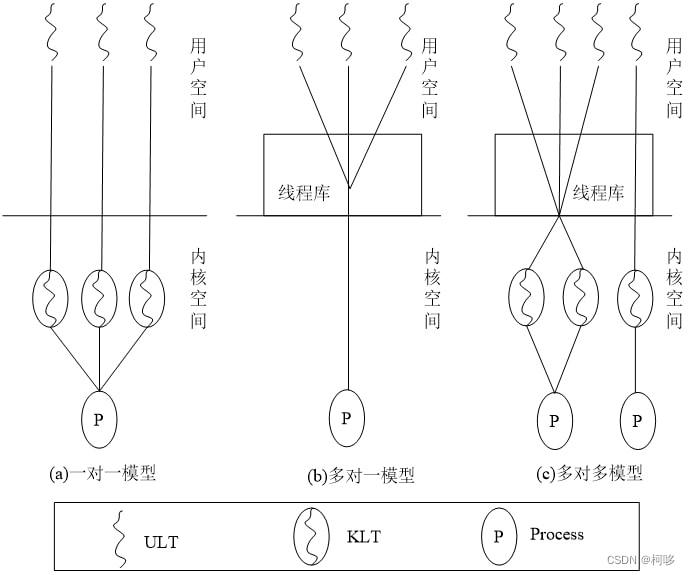
处理器管理补充——线程
传送门:操作系统——处理器管理http://t.csdnimg.cn/avaDO 1.1 线程的概念 回忆:[未引入线程前] 进程有两个基本属性:拥有资源的独立单位、处理器调度和分配的基本单位。 引入线程以后,线程将作为处理器调度和运行的基本单位&…...

RESTful 风格是指什么
RESTful(Representational State Transfer)是一种基于 HTTP 协议的软件架构风格,用于设计网络应用程序的接口。它的设计理念是利用 HTTP 协议中的方法(如 GET、POST、PUT、DELETE 等)来对资源进行 CRUD,使得…...

Python 二维矩阵加一个变量运算该如何避免 for 循环
Python 二维矩阵加一个变量运算该如何避免 for 循环 引言正文方法1------使用 for 循环方法2------不使用 for 循环引言 今天写代码的时候遇到了一个问题,比如我们需要做一个二维矩阵运算,其中一个矩阵是 2x2 的,另一个是 2x1 的。在这个二维矩阵中,其中各个参数会随着一个…...
Nginx 配置详解
官网:http://www.nginx.org/ 序言 Nginx是lgor Sysoev为俄罗斯访问量第二的rambler.ru站点设计开发的。从2004年发布至今,凭借开源的力量,已经接近成熟与完善。 Nginx功能丰富,可作为HTTP服务器,也可作为反向代理服务…...

python读写文件操作的三大基本步骤
目录 基本步骤 常用函数 open()函数 close()函数 read()函数 readlines()函数 readline()函数 write()函数 writelines()函数 with语句 读写操作的应用: 拷贝文件 with 语句的嵌套 逐行拷贝 基本步骤 1. 打开文件:open(filepath, mode, en…...

《Go 简易速速上手小册》第3章:数据结构(2024 最新版)
文章目录 3.1 数组与切片:Go 语言的动态队伍3.1.1 基础知识讲解3.1.2 重点案例:动态成绩单功能描述实现代码扩展功能 3.1.3 拓展案例 1:数据分析功能描述实现代码扩展功能 3.1.4 拓展案例 2:日志过滤器功能描述实现代码扩展功能 3…...

雷达模拟触摸屏,支持tuio\鼠标\Touch
案例展示: 雷达精度测试 星秒雷达互动软件测试 功能说明: 雷达互动系统支持各种品牌雷达,支持4-256点校准(校准点越大精度越高 ,而市场上基本都是4点校准 ,碰到大面积范围无法保证精准度)&…...
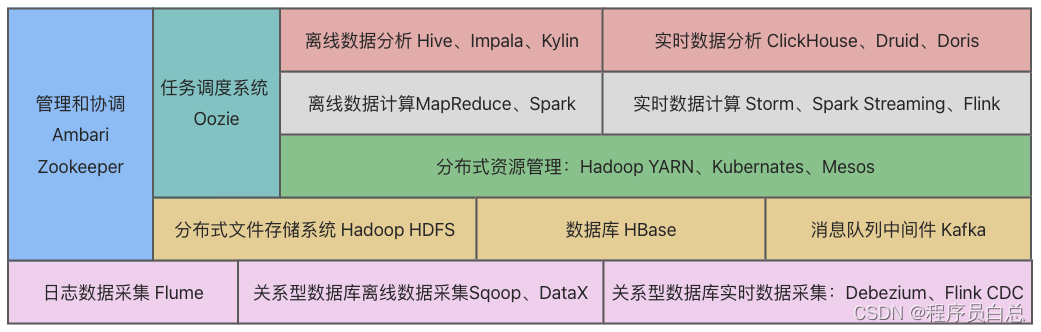
一文了解大数据生态
大数据一词最早指的是传统数据处理应用软件无法处理的过于庞大或过于复杂的数据集。 现在,对“大数据”一词的使用倾向于使用预测分析、用户行为分析或者其他一些从大数据中提取价值的高级数据分析方法,很少用于表示特定规模的数据集。 定义 大数据是…...
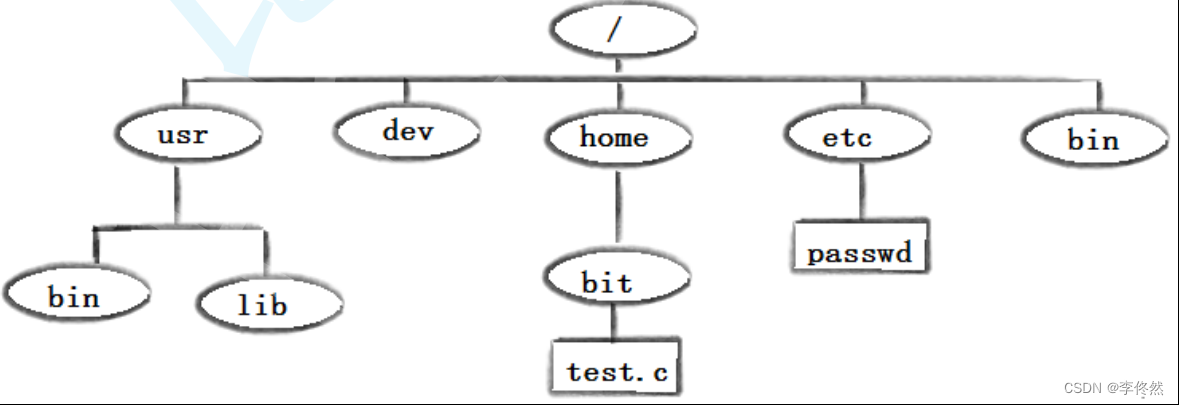
Linux篇:指令
一 基本常识: 1. 文件文件内容文件的属性 2. 文件的操作对文件内容的操作对文件属性的操作 3. 文件的类型: d:目录文件 -:普通文件 4. 指令是可执行程序,指令的代码文件在系统的某一个位置存在的。/u…...
)
Linux eject命令教程:如何控制可移动介质的弹出和收回(附案例详解和注意事项)
Linux eject命令介绍 eject命令在Linux中用于弹出可移动介质,通常是CD-ROM、软盘、磁带或JAZ或ZIP磁盘。您还可以使用此命令来控制一些多盘CD-ROM切换器,一些设备支持的自动弹出功能,以及关闭一些CD-ROM驱动器的光盘托盘。 Linux eject命令…...
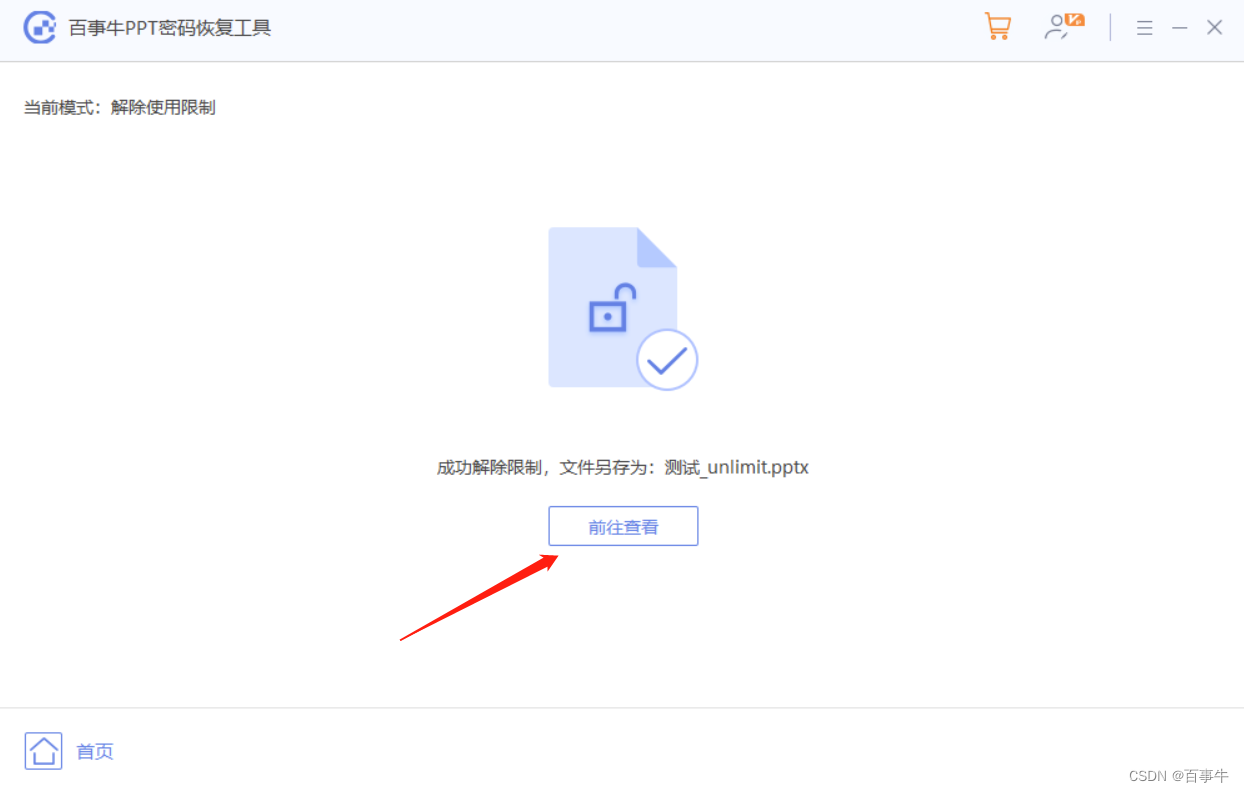
【已解决】PPT无法复制内容怎么办?
想要复制PPT文件里的内容,却发现复制不了,怎么办? 这种情况,一般是PPT文件被设置了以“只读方式”打开,“只读方式”下的PPT无法进行编辑更改,也无法进行复制粘贴的操作。 想要解决这个问题,我…...
六大设计原则 (SOLID)
一、设计原则概述 古人云: 有道无术,术可求.有术无道,止于术. 而设计模式通常需要遵循一些设计原则,在设计原则的基础之上衍生出了各种各样的设计模式。设计原则是设计要求,设计模式是设计方案,使用设计模式的代码则是具体的实现。 设计模式中主要有六大设计原则,简称为SOL…...

深度解析Sora的核心技术
Sora要解决的核心问题 Sora面临的挑战是将不同类型的视觉信息,如视频、文本、图像和声音等,整合为一种共同的表征形式。这种转换是实现统一训练过程的关键,旨在将各类数据集中到一个训练框架中,以便于进行大规模的统一学习。简而…...

设计模式面试系列-02
1. Java 中工厂模式有什么优势? 1、工厂模式是最常用的实例化对象模式,是用工厂方法代替new操作的一种模式。 2、利用工厂模式可以降低程序的耦合性,为后期的维护修改提供了很大的便利。 3、将选择实现类、创建对象统一管理和控制,从而将调用者跟我们的实现类解耦。 2. …...

MKdocs添加顶部公告栏
效果如图: docs/overrides下新建main.html ,针对main.html文件 树状结构如下: $ tree -a . ├── .github │ ├── .DS_Store │ └── workflows │ └── PublishMySite.yml ├── docs │ └── index.md │ └──overrides │…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
