【深度学习】Pytorch教程(八):PyTorch数据结构:2、张量的数学运算(6):高维张量:乘法、卷积(conv2d~四维张量;conv3d~五维张量)
文章目录
- 一、前言
- 二、实验环境
- 三、PyTorch数据结构
- 1、Tensor(张量)
- 1. 维度(Dimensions)
- 2. 数据类型(Data Types)
- 3. GPU加速(GPU Acceleration)
- 2、张量的数学运算
- 1. 向量运算
- 2. 矩阵运算
- 3. 向量范数、矩阵范数、与谱半径详解
- 4. 一维卷积运算
- 5. 二维卷积运算
- 6. 高维张量
- torch.matmul VS torch.mul
- 乘法计算原则
- 二维卷积conv2d(四维张量)
- 三维卷积conv3d(五维张量)
一、前言
卷积运算是一种在信号处理、图像处理和神经网络等领域中广泛应用的数学运算。在图像处理和神经网络中,卷积运算可以用来提取特征、模糊图像、边缘检测等。在信号处理中,卷积运算可以用来实现滤波器等操作。
二、实验环境
本系列实验使用如下环境
conda create -n DL python==3.11
conda activate DL
conda install pytorch torchvision torchaudio pytorch-cuda=12.1 -c pytorch -c nvidia
三、PyTorch数据结构
1、Tensor(张量)
Tensor(张量)是PyTorch中用于表示多维数据的主要数据结构,类似于多维数组,可以存储和操作数字数据。
1. 维度(Dimensions)
Tensor(张量)的维度(Dimensions)是指张量的轴数或阶数。在PyTorch中,可以使用size()方法获取张量的维度信息,使用dim()方法获取张量的轴数。
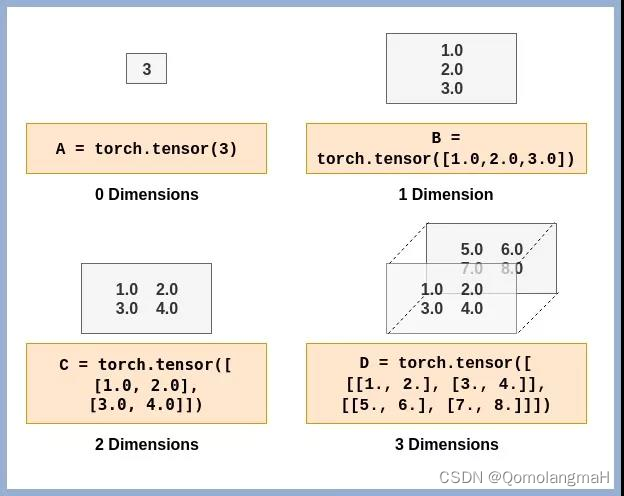
2. 数据类型(Data Types)
PyTorch中的张量可以具有不同的数据类型:
- torch.float32或torch.float:32位浮点数张量。
- torch.float64或torch.double:64位浮点数张量。
- torch.float16或torch.half:16位浮点数张量。
- torch.int8:8位整数张量。
- torch.int16或torch.short:16位整数张量。
- torch.int32或torch.int:32位整数张量。
- torch.int64或torch.long:64位整数张量。
- torch.bool:布尔张量,存储True或False。
【深度学习】Pytorch 系列教程(一):PyTorch数据结构:1、Tensor(张量)及其维度(Dimensions)、数据类型(Data Types)
3. GPU加速(GPU Acceleration)
【深度学习】Pytorch 系列教程(二):PyTorch数据结构:1、Tensor(张量): GPU加速(GPU Acceleration)
2、张量的数学运算
PyTorch提供了丰富的操作函数,用于对Tensor进行各种操作,如数学运算、统计计算、张量变形、索引和切片等。这些操作函数能够高效地利用GPU进行并行计算,加速模型训练过程。
1. 向量运算
【深度学习】Pytorch 系列教程(三):PyTorch数据结构:2、张量的数学运算(1):向量运算(加减乘除、数乘、内积、外积、范数、广播机制)
2. 矩阵运算
【深度学习】Pytorch 系列教程(四):PyTorch数据结构:2、张量的数学运算(2):矩阵运算及其数学原理(基础运算、转置、行列式、迹、伴随矩阵、逆、特征值和特征向量)
3. 向量范数、矩阵范数、与谱半径详解
【深度学习】Pytorch 系列教程(五):PyTorch数据结构:2、张量的数学运算(3):向量范数(0、1、2、p、无穷)、矩阵范数(弗罗贝尼乌斯、列和、行和、谱范数、核范数)与谱半径详解
4. 一维卷积运算
【深度学习】Pytorch 系列教程(六):PyTorch数据结构:2、张量的数学运算(4):一维卷积及其数学原理(步长stride、零填充pad;宽卷积、窄卷积、等宽卷积;卷积运算与互相关运算)
5. 二维卷积运算
【深度学习】Pytorch 系列教程(七):PyTorch数据结构:2、张量的数学运算(5):二维卷积及其数学原理
6. 高维张量
torch.matmul VS torch.mul
torch.matmul:用于执行两个张量的矩阵乘法操作,它要求两个张量的维度需要满足矩阵乘法的规则,例如对于两个三维张量,torch.matmul将在最后两个维度上执行矩阵乘法。
import torch# 创建两个张量
tensor1 = torch.randn(3, 4)
tensor2 = torch.randn(4, 5) # 矩阵乘法
result = torch.matmul(tensor1, tensor2)
print(result.shape)
-
torch.mul:用于对两个张量进行逐元素相乘,即*运算符,会将两个张量的每个元素进行相乘。要求两个张量的形状需要一致或者满足广播规则。 -
对比
import torchtensor1 = torch.tensor([[1, 2, 3],[4, 5, 6]]) # shape: (2, 3)tensor2 = torch.tensor([[7, 8],[9, 10],[11, 12]]) # shape: (3, 2)# 使用 torch.matmul 进行矩阵乘法
result_matmul = torch.matmul(tensor1, tensor2) # 结果为 shape (2, 2)
print("Matmul result:")
print(result_matmul)# 使用 torch.mul 进行逐元素相乘
result_mul = torch.mul(tensor1, tensor2.T) # 结果为逐元素相乘后的张量
print("\nMul result:")
print(result_mul)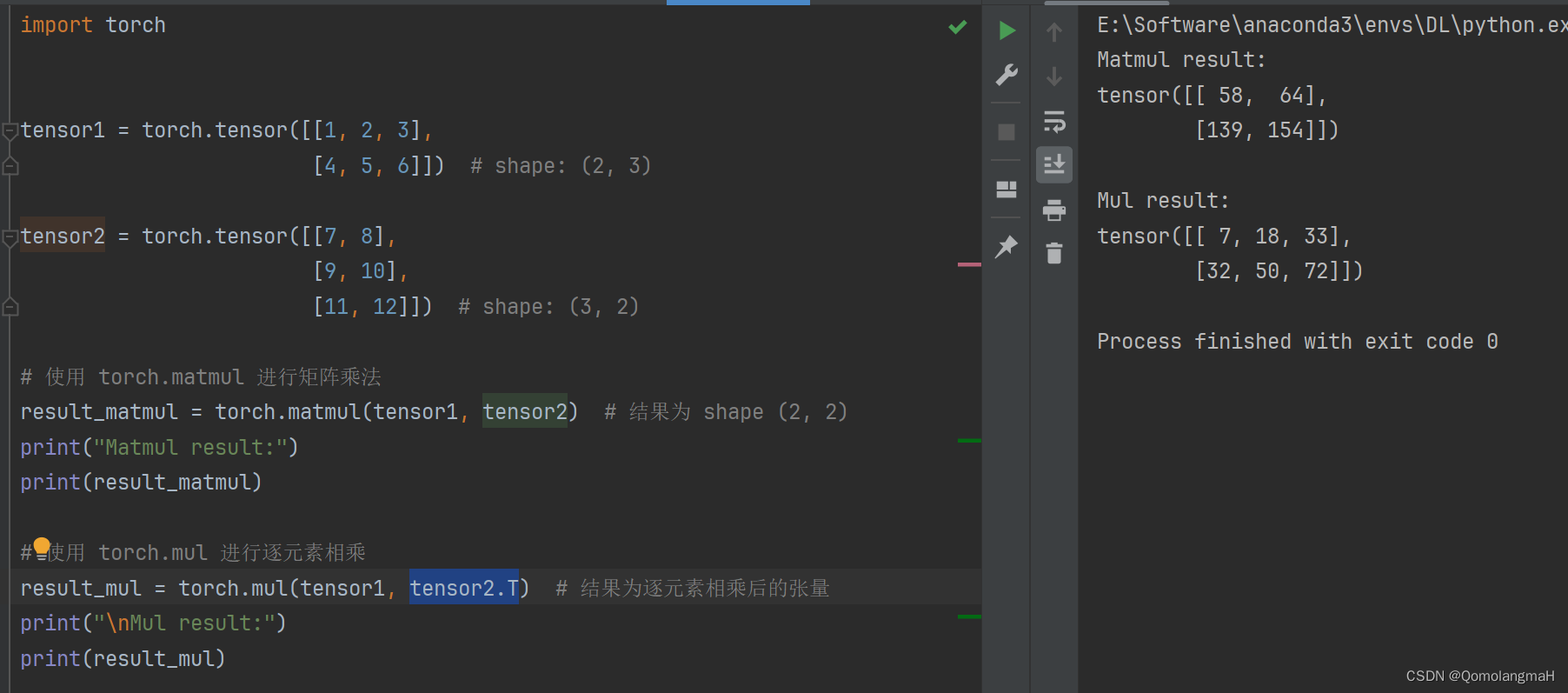
乘法计算原则
-
张量的维度匹配:两个张量进行乘法操作时,需要保证它们的维度匹配。例如,两个张量的维度分别为(a,b,c)和(c,d),那么它们可以进行乘法操作。
-
批量乘法:如果两个张量的维度不完全匹配,但它们在最后一维上相符,那么可以进行批量乘法。这意味着两个张量的前面维度需要匹配,并且其中一个张量的维度需要和另一个张量的倒数第二个维度相匹配。
import torchtensor1 = torch.randn(3, 4, 5) # 维度为 (3, 4, 5)
tensor2 = torch.randn(3, 5, 6) # 维度为 (3, 5, 6)
result = torch.matmul(tensor1, tensor2)print(result.size()) # 输出为 (3, 4, 6),说明两个张量进行了批量乘法
- 广播机制:如果两个张量的维度不完全匹配,但是可以通过广播机制进行维度的扩展以匹配,那么可以进行乘法操作。广播机制会自动将维度较小的张量扩展到维度较大的张量上。
import torchtensor1 = torch.tensor([[1, 2, 3],[4, 5, 6]]) # shape: (2, 3)tensor2 = torch.tensor([[7, 8],[9, 10],[11, 12]]) # shape: (3, 2)tensor3 = torch.cat([tensor1, tensor1], dim=1)# 通过 unsqueeze 添加新的维度来复制成三维张量
# tensor1_3d = tensor1.unsqueeze(0) # 在第一个维度上添加新的维度
# print(tensor1_3d.shape) # 输出:(1, 2, 3)
tensor1_3d = tensor1.expand(2, 2, 3) # 扩展维度
print(tensor1_3d.shape) # 输出:(2, 2, 3)
print(tensor1_3d)result_matmul1 = torch.matmul(tensor1, tensor2)
print(f"{tensor1.size()}*{tensor2.size()}={result_matmul1.size()}")
print(result_matmul1)result_matmul2 = torch.matmul(tensor1_3d, tensor2)
print(f"{tensor1_3d.size()}*{tensor2.size()}={result_matmul2.size()}")
print(result_matmul2)result_matmul3 = torch.matmul(tensor2, tensor1)
print(f"{tensor2.size()}*{tensor1.size()}={result_matmul3.size()}")
print(result_matmul3)result_matmul4 = torch.matmul(tensor2, tensor1_3d)
print(f"{tensor2.size()}*{tensor1_3d.size()}={result_matmul4.size()}")
print(result_matmul4)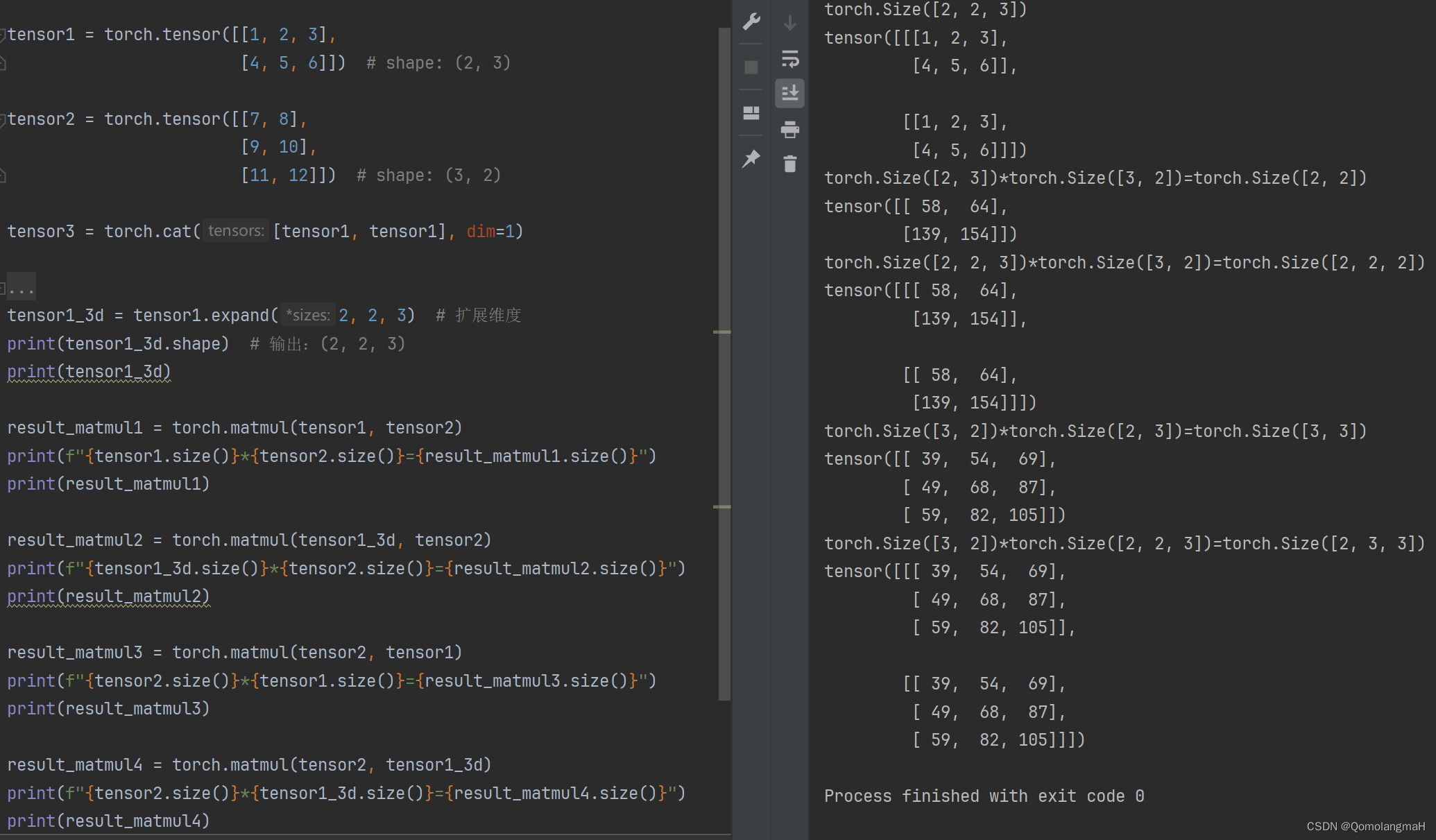
二维卷积conv2d(四维张量)
import torch
import torch.nn.functional as F# batch_size=2, channel=3, height=32, width=32
input_tensor = torch.randn(2, 3, 32, 32)# out_channels=4, in_channels=3, kernel_height=3, kernel_width=3
conv_kernel = torch.randn(4, 3, 3, 3)# 执行卷积操作
output = F.conv2d(input_tensor, conv_kernel, padding=1)print(output.size()) # 输出为 (2, 4, 32, 32)
-
通道匹配:卷积核的输入通道数必须与输入张量的通道数相同( 3 = 3 3=3 3=3),这样才能进行逐通道的卷积操作。
-
大小匹配:卷积核的大小必须小于或等于输入张量的大小( 3 < 32 3<32 3<32),否则无法在输入张量上进行卷积操作。
-
卷积参数:
- 步长:卷积时的步长参数需要考虑输入张量的大小;
- 填充:填充参数可以用来控制卷积操作的输出尺寸,用于保持输入和输出的尺寸一致。
三维卷积conv3d(五维张量)
import torch
import torch.nn.functional as F#batch_size=2, channel=3, depth=10, height=32, width=32
input_tensor = torch.randn(2, 3, 10, 32, 32)# out_channels=4, in_channels=3, kernel_depth=3, kernel_height=3, kernel_width=3
conv_kernel = torch.randn(4, 3, 3, 3, 3)
# 执行三维卷积操作
output = F.conv3d(input_tensor, conv_kernel, padding=1)print(output.size()) # 输出为 (2, 4, 10, 32, 32)
相关文章:

【深度学习】Pytorch教程(八):PyTorch数据结构:2、张量的数学运算(6):高维张量:乘法、卷积(conv2d~四维张量;conv3d~五维张量)
文章目录 一、前言二、实验环境三、PyTorch数据结构1、Tensor(张量)1. 维度(Dimensions)2. 数据类型(Data Types)3. GPU加速(GPU Acceleration) 2、张量的数学运算1. 向量运算2. 矩阵…...

Autosar-Mcal配置详解-GPT
3.3.1添加GPT模块 方法与添加Dio相似,可参加Dio模块添加方法。 3.3.2 创建、配置GPT通道 1)根据需求创建GPT通道(即创建几个定时器) 本例中创建了3个定时器通道:1ms,100us,OsTimer。 2)配置GPT通道 配置T…...
)
前端面试问题(jwt/布局/vue数组下标/扁平化/菜单树形/url api/新版本)
前端面试问题(jwt/布局/vue数组下标/扁平化/菜单树形/url api/新版本) 1. jwt鉴权逻辑 前端 JWT 鉴权逻辑通常涉及在发起请求时携带 JWT,并在接收到响应后处理可能的授权问题。 1. 用户登录: 用户提供凭证: 用户在登录界面输入用户名和密码…...
Learn HTML in 1 hour
website address https://www.youtube.com/watch?vHD13eq_Pmp8 excerpt All right, what’s going on? everybody. It’s your Bro, hope you’re doing well, and in this video I’m going to help you started with html; so sit back, relax and enjoy the show. If y…...

HashMap的put方法执行过程
根据Key通过哈希算法与与运算得出数组下标如果数组下标位置元素为空,则将key和value封装为Entry对象(JDK1.7中是Entry对象,JDK1.8中 是Node对象)并放⼊该位置如果数组下标位置元素不为空,则要分情况讨论 a. 如果是JDK1…...
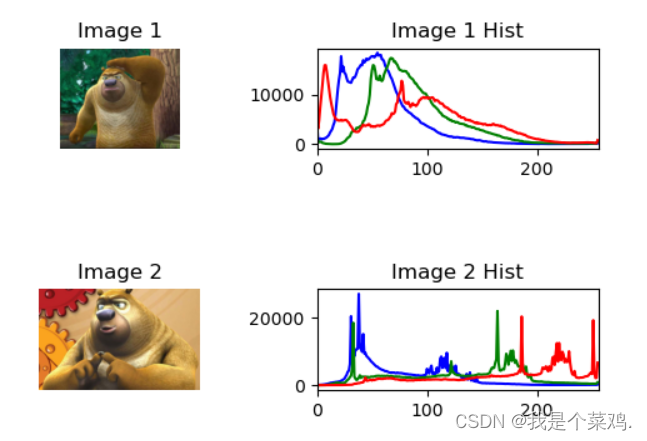
一、直方图相关学习
目录 1、灰度直方图1.1 基本概念和作用1.2 代码示例 2、BGR直方图2.1 基本概念和作用2.2 代码示例 3、灰度直方图均衡1. 基本概念和作用2. 代码示例 4、直方图变换(查找)4.1 基本概念和作用4.2 代码示例 5、直方图匹配5.1 基本概念和作用5.2 代码示例 6、…...

Linux 权限详解
目录 一、权限的概念 二、权限管理 三、文件访问权限的相关设置方法 3.1chmod 3.2chmod ax /home/abc.txt 一、权限的概念 Linux 下有两种用户:超级用户( root )、普通用户。 超级用户:可以再linux系统下做任何事情ÿ…...
零基础学习8051单片机(十五)
本次先看书学习,并完成了课后习题,题目出自《单片机原理与接口技术》第五版—李清朝 答: (1)当 CPU正在处理某件事情的时候,外部发生的某一件事件请求 CPU 迅速去处理,于是,CPU暂时中止当前的工…...

项目的一些难点
1.不用redis?分布式锁,如何防止用户重复点击? 1.乐观锁 乐观锁是一种在数据库层面上避免并发冲突的机制。它通常通过在数据库记录中添加一个版本号(或时间戳)来实现。每次更新记录时,都会检查版本号是否与数据库中的…...

Kubernetes 卷存储 NFS | nfs搭建配置 原理介绍 nfs作为存储卷使用
1、NFS介绍 NFS(Network File System)是一种分布式文件系统协议,允许客户端远程访问服务器上的文件,实现数据共享。它整合多个存储设备为统一文件系统,方便数据存储和管理,支持负载均衡和故障转移…...
开启智能互动新纪元——ChatGPT提示词工程的引领力
目录 提示词工程的引领力 高效利用ChatGPT提示词方法 提示词工程的引领力 近年来,随着人工智能技术的迅猛发展,ChatGPT提示词工程正逐渐崭露头角,为智能互动注入了新的活力。这一技术的引入,使得人机交流更加流畅、贴近用户需求&…...
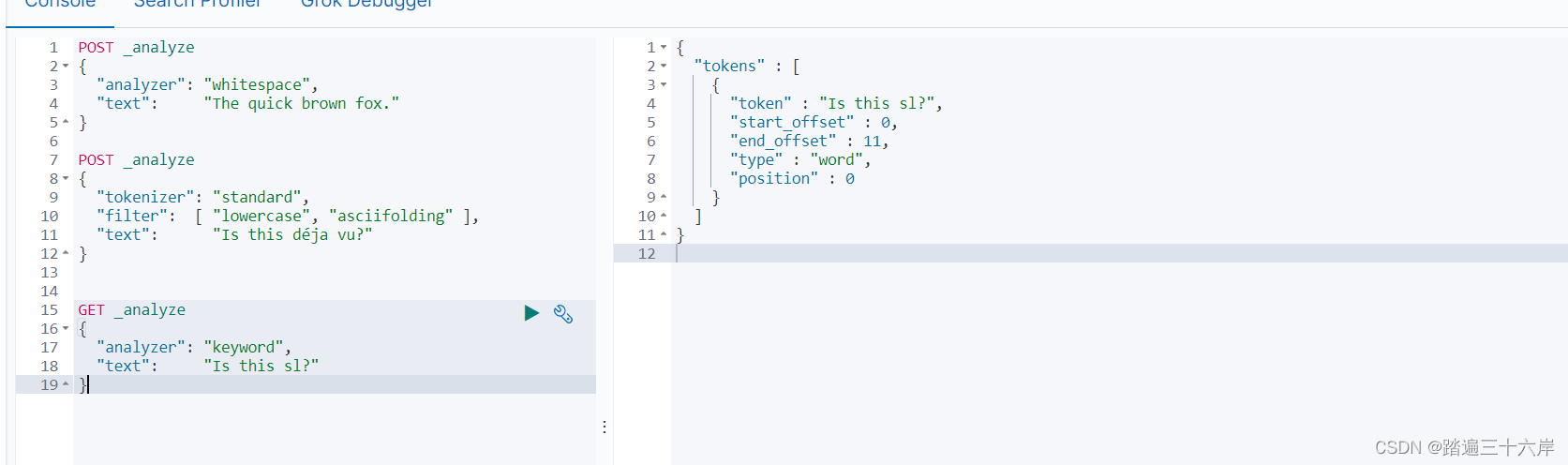
ElasticSearch语法
Elasticsearch 概念 入门学习: Index索引>MySQL 里的表(table)建表、增删改查(查询需要花费的学习时间最多)用客户端去调用 ElasticSearch(3 种)语法:SQL、代码的方法(4 种语法) ES 相比于 MySQL,能够自动帮我们做分词,能够非常高效、灵活地查询内…...

SMT贴片加工厂需要哪些加工资料
SMT贴片加工中在评估报价的时候需要给到SMT贴片加工厂以下资料,以便工程师和采购进行工艺和报价评估。 在SMT加工中如果需要供应商提供一站式的加工服务,那么在前期就需要更频繁的沟通和配合,包工包料服务是需要PCB制板资料和制板说明、BOM清…...
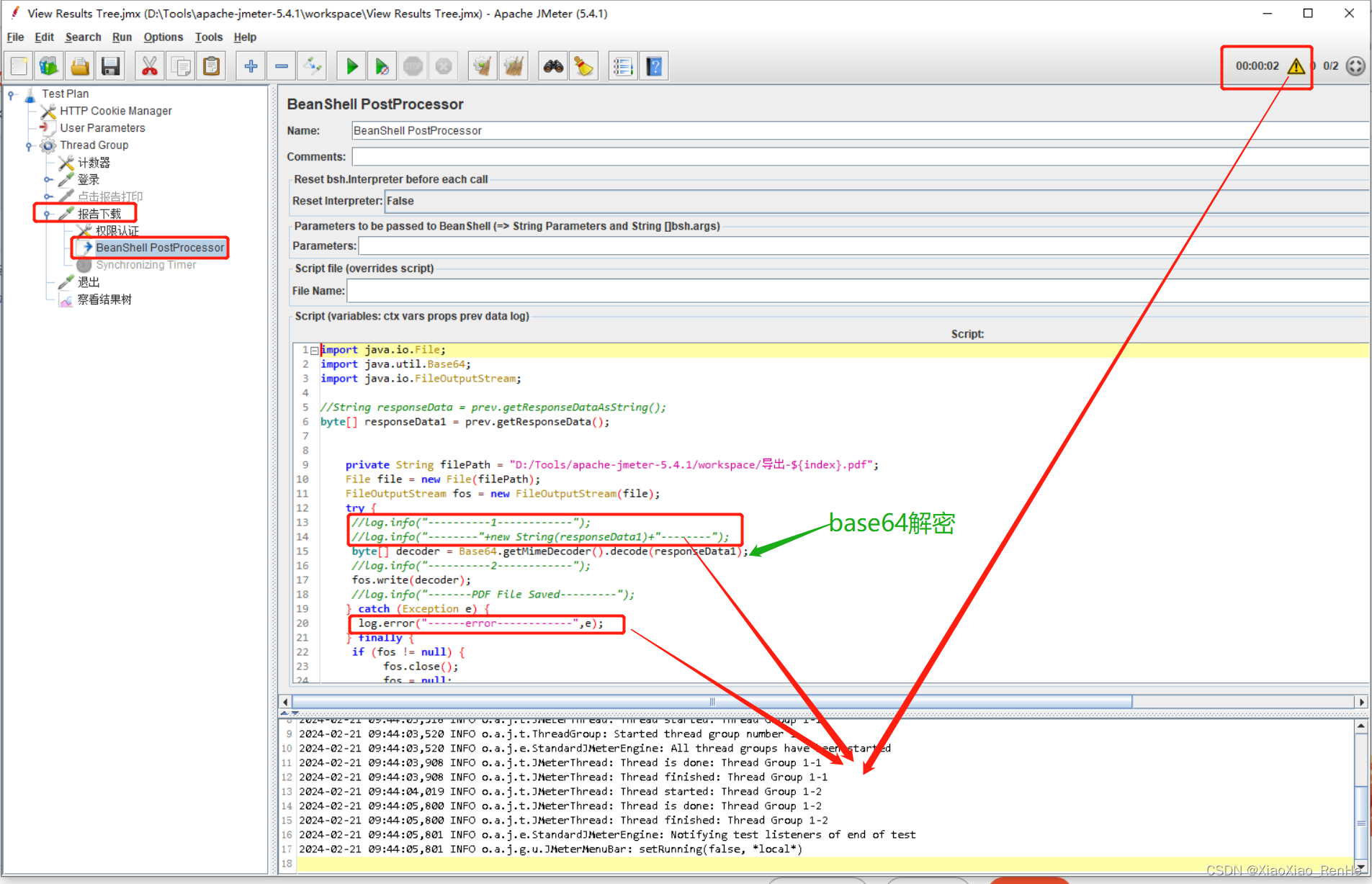
jmeter下载base64加密版pdf文件
一、何为base64加密版pdf文件 如下图所示,接口jmeter执行后,返回一串包含大小写英文字母、数字、、/、的长字符串,直接另存为pdf文件后,文件有大小,但是打不开;另存为doc文件后,打开可以看到和…...
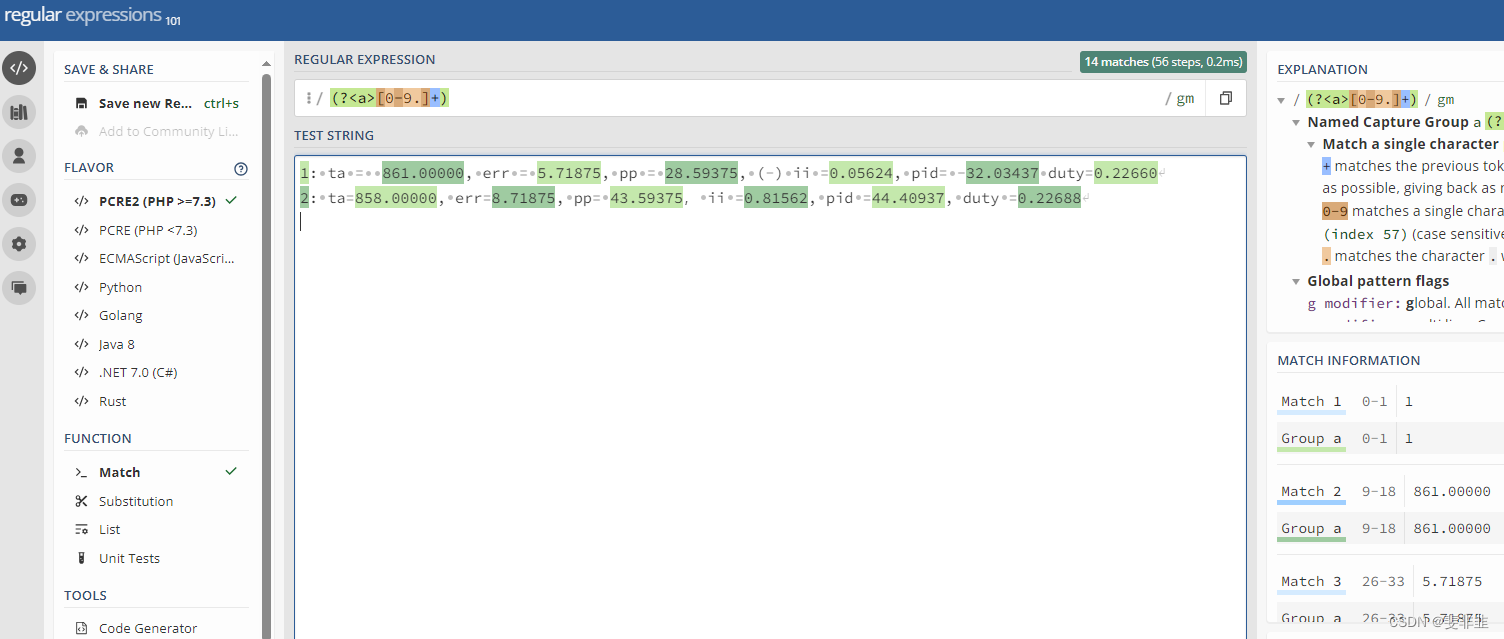
【regex】正则表达式
集合 [0-9.] [0-9.\-] 例子 正则表达式,按照规则写,写的时候应该不算困难,但是可读性差 不同语言中regex会有微小的差异 vim 需要转义, perl/python中不需要转义 锚位 \b am\b i am 命名 / 命名捕获组 ( 捕获组(…...

78.Spring和SpringBoot的关系和区别?
一、Spring和SpringBoot的关系和区别 SpringBoot是Spring生态的产品。 Spring Framework是一个容器框架 SpringBoot 它不是一个框架、它是一个可以快速构建基于Spring的脚手架(里面包含了Spring和各种框架),为开发Spring生态其他框架铺平道路࿰…...
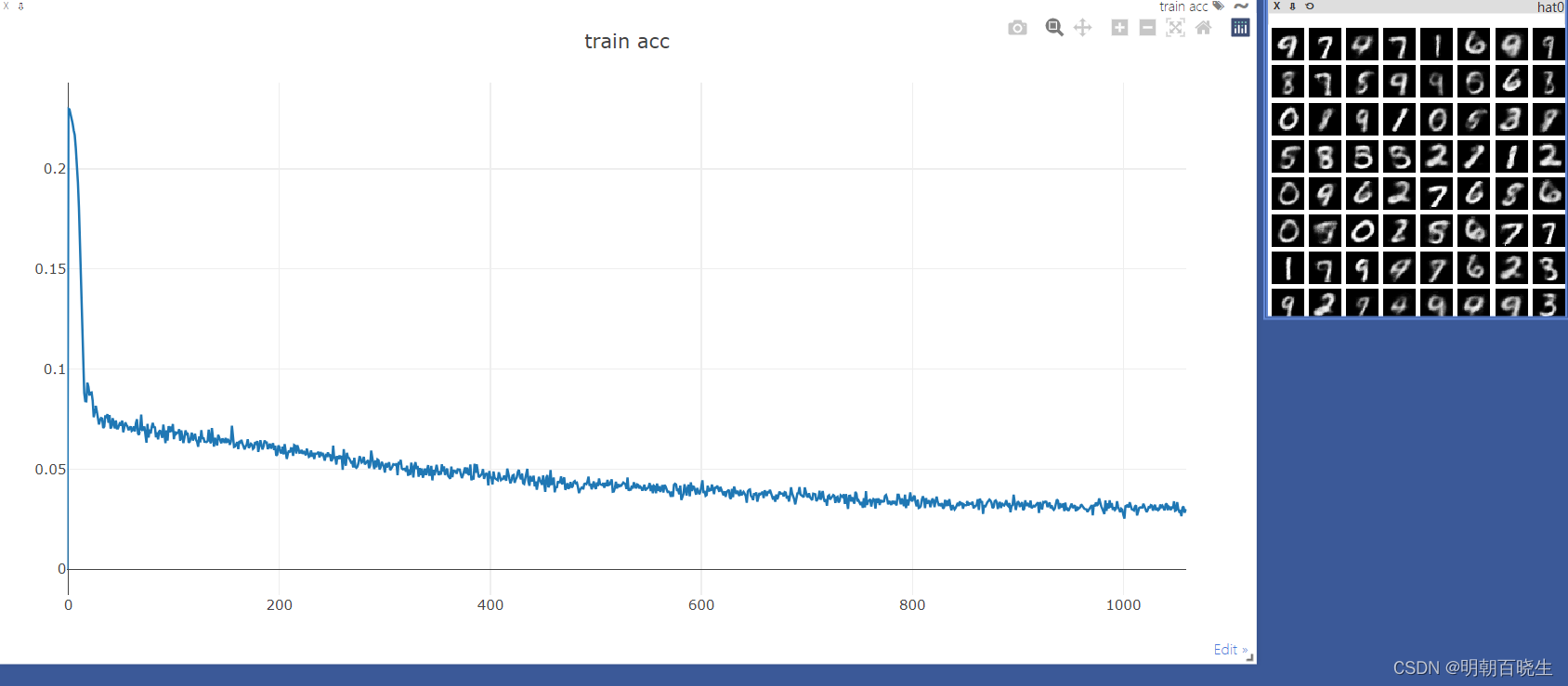
【PyTorch][chapter 17][李宏毅深度学习]【无监督学习][ Auto-encoder]
前言: 本篇重点介绍AE(Auto-Encoder) 自编码器。这是深度学习的一个核心模型. 自编码网络是一种基于无监督学习方法的生成类模型,自编码最大特征输出等于输入 Yann LeCun&Bengio, Hinton 对无监督学习的看法. 目录: AE 模型原…...

Modern C++ std::variant的实现原理
前言 std::variant是C17标准库引入的一种类型,用于安全地存储和访问多种类型中的一种。它类似于C语言中的联合体(union),但功能更为强大。与联合体相比,std::variant具有类型安全性,可以判断当前存储的实际…...

⭐北邮复试刷题LCR 018. 验证回文串__双指针 (力扣119经典题变种挑战)
LCR 018. 验证回文串 给定一个字符串 s ,验证 s 是否是 回文串 ,只考虑字母和数字字符,可以忽略字母的大小写。 本题中,将空字符串定义为有效的 回文串 。 示例 1: 输入: s “A man, a plan, a canal: Panama” 输出: true 解释…...

C++面试:数据库的权限管理数据库的集群和高可用
目录 一、数据库的权限管理 1. 用户和角色管理 用户管理 实例举例(以MySQL为例): 角色管理 实例举例(以MySQL为例): 总结 2. 权限和授权 用户和角色管理 用户管理 角色管理 权限和授权 权限 授…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
