【海贼王的数据航海:利用数据结构成为数据海洋的霸主】时间复杂度 | 空间复杂度
目录
1 -> 算法效率
1.1 -> 如何衡量一个算法的好坏?
1.2 -> 算法的复杂度
2 -> 时间复杂度
2.1 -> 时间复杂度的概念
2.2 -> 大O的渐进表示法
2.3 -> 常见时间复杂度计算
3 -> 空间复杂度
4 -> 常见复杂度对比

1 -> 算法效率
1.1 -> 如何衡量一个算法的好坏?
对于以下斐波那契数列:
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
using namespace std;long long fib(int N)
{if (N < 3)return 1;return fib(N - 1) + fib(N - 2);
}int main()
{return 0;
}用递归实现斐波那契数列,看上去代码十分简洁,但简洁一定就是好算法吗?如何衡量一个算法的好坏?
1.2 -> 算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机存储容量很小。所以对于空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要特别关注一个算法的空间复杂度。
2 -> 时间复杂度
2.1 -> 时间复杂度的概念
定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上来讲,是不能算出来的,只有把程序放在机器上跑起来才能知道。但是我们需要每个算法都上机测试吗?固然可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方法。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
#define _CRT_SECURE_NO_WARNINGS#include <iostream>
using namespace std;// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i)for (int j = 0; j < N; ++j)++count;for (int k = 0; k < 2 * N; ++k)++count;int M = 10;while (M--)++count;cout << count << endl;
}int main()
{return 0;
}Func1执行的基本操作数:
-> N = 10 F(N) = 130-> N = 100 F(N) = 10210-> N = 1000 F(N) = 1002010
实际我们在计算时间复杂度时,并不一定要计算精确的执行次数,只需要大概执行次数,所以我们使用大O的渐进表示法。
2.2 -> 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
- 在常数1取代运行时间中的所有加法常数;
- 在修改后的运行次数函数中,只保留最高阶项;
- 如果最高阶项存在且不为1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法后,Func1的时间复杂度为:
-> N = 10 F(N) = 100
-> N = 100 F(N) = 10000-> N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
- 最好情况:任意输入规模的最小运行次数(下界)
- 平均情况:任意输入规模的期望运行次数
- 最坏情况:任意输入规模的最大运行次数(上界)
例如:在一个长度为N的数组中搜索一个数据x
- 最好情况:1次找到
- 平均情况:N / 2次找到
- 最坏情况:N次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中的搜索数据时间复杂度为:
2.3 -> 常见时间复杂度计算
实例1:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k)++count;int M = 10;while (M--)++count;cout << count << endl;
}实例2:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k)++count;for (int k = 0; k < N; ++k)++count;cout << count << endl;
}实例3:
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; ++k)++count;cout << count << endl;
}实例4:
// 计算strchr的时间复杂度?
const char* strchr(const char* str, int character);实例5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}实例6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;// [begin, end]:begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}实例7:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}实例8:
// 计算斐波那契递归fib的时间复杂度?
long long fib(size_t N)
{if (N < 3)return 1;return fib(N - 1) + fib(N - 2);
}答案及分析:
1. 实例1基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)2. 实例2基本操作执行了M+N次,有两个未知数M和N,时间复杂度为 O(N+M)3. 实例3基本操作执行了10次,通过推导大O阶方法,时间复杂度为 O(1)4. 实例4基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)5. 实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N^2)6. 实例6基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(logN) ps:logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN。7. 实例7通过计算分析发现基本操作递归了N次,时间复杂度为O(N)。8. 实例8通过计算分析发现基本操作递归了2^N次,时间复杂度为O(2^N)。
3 -> 空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少byte的空间,因为意义不大,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本与时间复杂度类似,也是使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时显式申请的额外空间来确定。
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}实例2:
// 计算fib的空间复杂度?
// 返回斐波那契数列的前n项
long long* fib(size_t n)
{if (n == 0)return NULL;long long* arr = (long long*)malloc((n + 1) * sizeof(long long));arr[0] = 0;arr[1] = 1;for (int i = 2; i <= n; ++i)arr[i] = arr[i - 1] + arr[i - 2];return arr;
}实例3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}答案及分析:
1. 实例1使用了常数个额外空间,所以空间复杂度为 O(1)2. 实例2动态开辟了N个空间,空间复杂度为 O(N)3. 实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
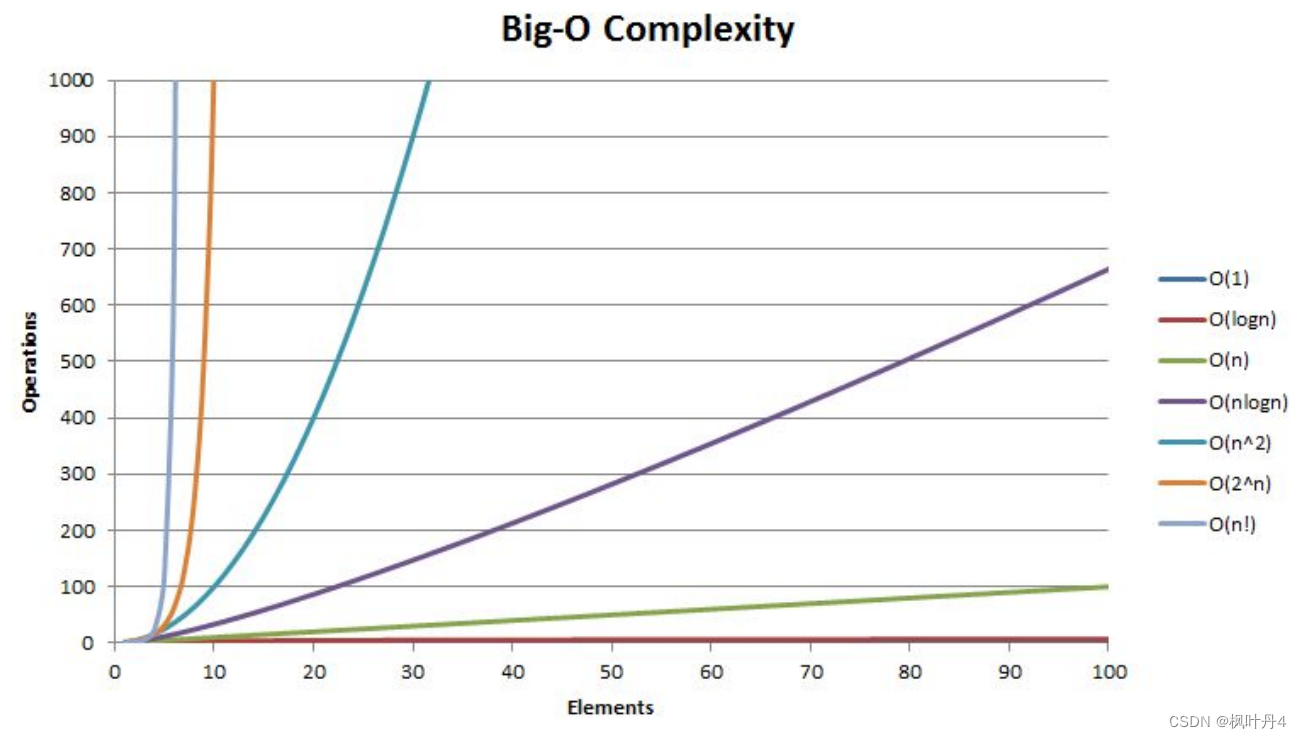
4 -> 常见复杂度对比
一般算法的常见复杂度:
| 5201314 | O(1) | 常数阶 |
| 3n + 4 | O(n) | 线性阶 |
| 3n ^ 2 + 4n + 5 | O(n ^ 2) | 平方阶 |
| 3log(2)n + 4 | O(logn) | 对数阶 |
| 2n + 3nlog(2)n + 4 | O(nlogn) | nlogn阶 |
| n ^ 3 + n ^ 2 + 3n + 4 | O(n ^ 3) | 立方阶 |
| 2 ^ n | O(2 ^ n) | 指数阶 |
感谢大佬们支持!!!
互三啦!!!
相关文章:

【海贼王的数据航海:利用数据结构成为数据海洋的霸主】时间复杂度 | 空间复杂度
目录 1 -> 算法效率 1.1 -> 如何衡量一个算法的好坏? 1.2 -> 算法的复杂度 2 -> 时间复杂度 2.1 -> 时间复杂度的概念 2.2 -> 大O的渐进表示法 2.3 -> 常见时间复杂度计算 3 -> 空间复杂度 4 -> 常见复杂度对比 1 -> 算法效…...

OpenTiny Vue 组件库适配微前端可能遇到的4个问题
本文由体验技术团队 TinyVue 项目成员岑灌铭同学创作。 前言 微前端是一种多个团队通过独立发布功能的方式来共同构建现代化 web 应用的技术手段及方法策略,每个应用可以选择不同的技术栈,独立开发、独立部署。 TinyVue组件库的跨技术栈能力与微前端十…...
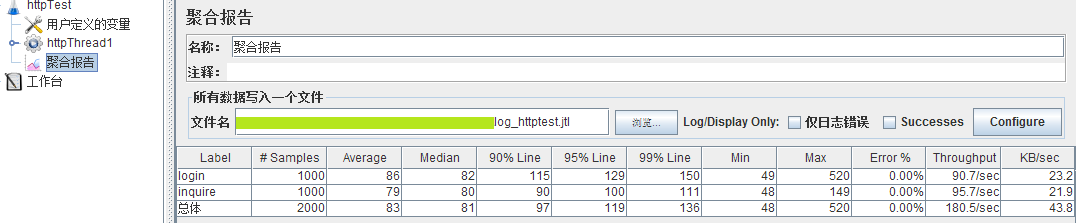
jmeter 命令行启动 动态参数化
[Jmeter命令行参数] 一、在linux中,使用非gui的方式执行jmeter。若需更改参数,必须先编辑jmx文件,找到对应的变量进行修改,比较麻烦。因此,可以参数化一些常用的变量,直接在Jmeter命令行进行设置 二、参数…...

C++跨模块释放内存
linux一个进程只有一个堆,不要考虑这些问题,但是windows一个进程可能有多个堆,要在对应的堆上释放。 一, MT改MD 一个进程的地址空间是由一个可执行模块和多个DLL模块构成的,这些模块中,有些可能会链接到…...

jQuery浅析
jQuery 是一个快速、简洁的 JavaScript 库,旨在简化 HTML 文档遍历、事件处理、动画以及 Ajax 交互等功能。由 John Resig 在2006年创建,它极大地简化了JavaScript开发人员在处理网页文档、选择DOM元素以及执行各种效果和功能时的工作。 核心特性&#x…...
)
分班问题 、幼儿园分班(C语言)
题目 幼儿园两个班的小朋友排队时混在了一起,每个小朋友都知道自己跟前面一个小朋友是不是同班,请你帮忙把同班的小朋友找出来 小朋友的编号为整数,与前面一个小朋友同班用Y表示,不同班用N表示 输入 输入为空格分开的小朋友编号…...

QT 如何让多语言翻译变得简单,提高效率?
一.QT多语言如何翻译的? 在QT的多语言翻译过程中,分为两个步骤:第一步生成ts文件,第二步将ts文件翻译为qm文件。如果我们在需要多语言的情况下,qml经常使用qstr或者qwidget中使用tr等等,遍布许多个文件夹,在需要更新新的翻译时会很麻烦。整个工程收索并修改,效率十分低…...

线性代数:线性方程组解的结构
目录 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3...

mysql之CRUD常见函数union查询
select select * from c insert 字段设置自增后,当我们指定增加一条数据后,往后增加的数据都会在该条数据后进行递增,但是可以认为的指定增加某条id不存在的数据 insert into c values(7,‘政治’) insert into c(c2) values(‘历史1’),(…...

开窗函数实践-实现两行记录之间计算时间差
一、需求背景 基于保密要求,不放原始表,新建测试表用来演示 insert into TEST0221 (采血人, 采血时间, 条码号, 病人ID) values (张三, to_date(21-02-2024 12:00:00, dd-mm-yyyy hh24:mi:ss), 2024001, 0001);insert into TEST0221 (采血人, 采血时间…...

String字符串的常见方法总结
目录 一、int length():返回字符串的长度 二、char charAt(int index):返回某索引处的字符 三、boolean isEmpty():判断字符串是否为空 四、String toUpperCase():将字符转换成大写 五、String toLowerCase():将字符转换成小写 六、String trim():去除首尾空白…...
Listen / Notify与事务的联动机制)
Postgresql源码(122)Listen / Notify与事务的联动机制
前言 Notify和Listen是Postgresql提供的不同会话间异步消息通信功能,例子: LISTEN virtual; NOTIFY virtual; Asynchronous notification "virtual" received from server process with PID 8448. NOTIFY virtual, This is the payload; Asy…...
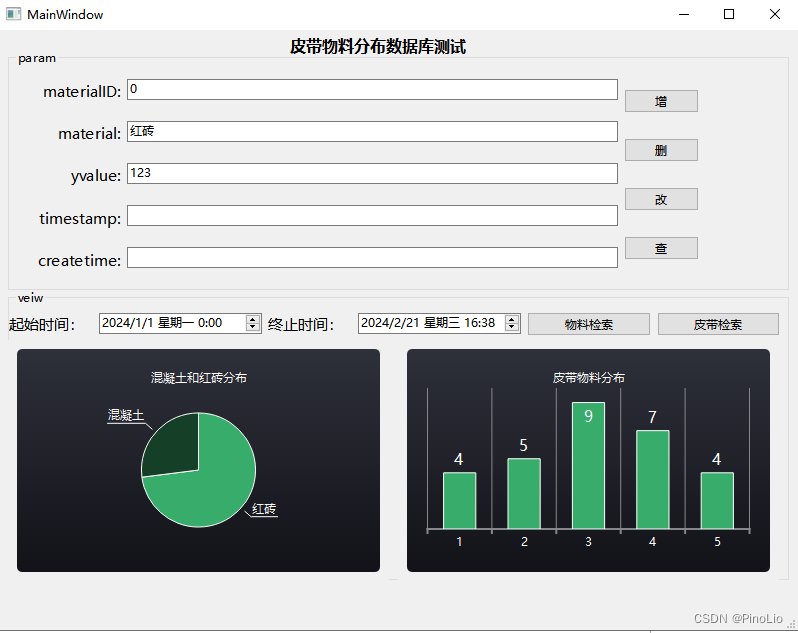
QT 数据库的增加操作和画图 Win
第一步、先配置CMakeLists.txt 在CMakeLists.txt中添加 find_package(Qt6 REQUIRED COMPONENTS Sql) find_package(Qt6 REQUIRED COMPONENTS Charts)target_link_libraries(${PROJECT_NAME} PRIVATE Qt6::Sql) target_link_libraries(${PROJECT_NAME} PRIVATE Qt6::Charts)避…...

【JS逆向学习】同花顺(q.10jqka)补环境
逆向目标 目标网址:https://q.10jqka.com.cn/ 目标接口: https://q.10jqka.com.cn/index/index/board/all/field/zdf/order/desc/page/3/ajax/1/ 目标参数:cookie 逆向过程 老规矩,先分析网络请求,发现是 cookie 加…...
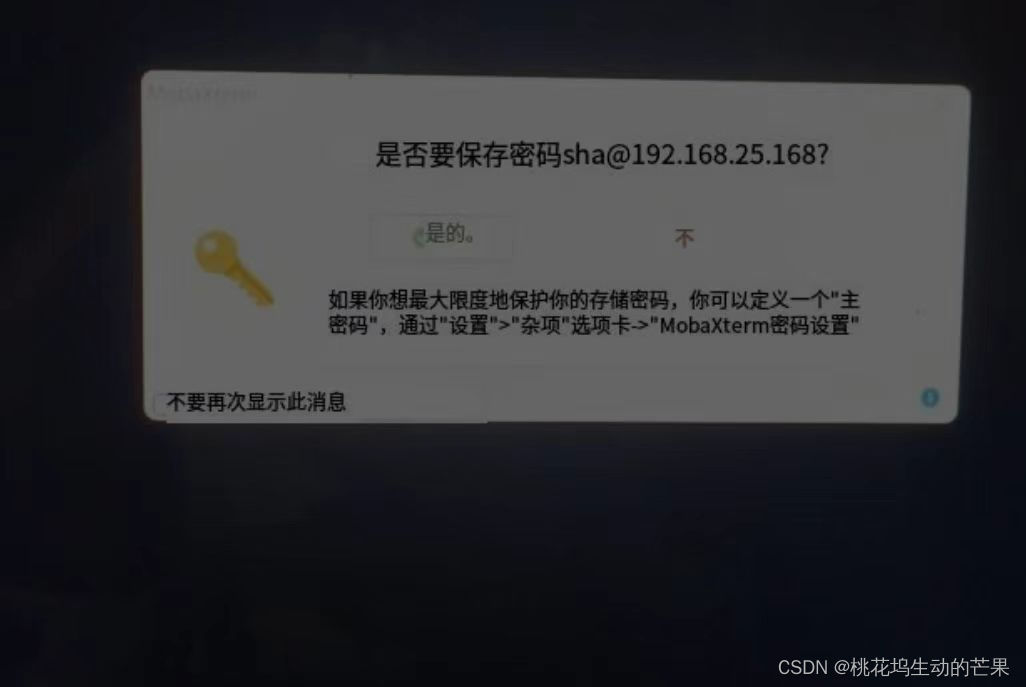
解决MobaXterm网络错误连接超时问题
报错页面: 报错原因: ①网络断开了 ②网络端口,端口号改变 解决办法: ①重新连接网络按R ②固定端口号 第一步:编辑------>虚拟机网络编辑器(我的Linux在虚拟机里) 第二步:用…...

突发!AI独角兽「竹间智能」被曝停工停产6个月
大家好我是二狗。 今天早上起来刷朋友圈,看到一张截图——AI创企竹间智能,宣称因为公司所处的经营环境艰难,部分部门和岗位将从即日起停工停产6个月。 图源:(企服科学) 下面是文字版: 由于公司…...

Qt应用软件【协议篇】GPIO控制LED灯
GPIO简介 GPIO(General Purpose Input/Output,通用输入输出)是一种通用的端口定义,在各种计算机、嵌入式系统和微控制器中广泛应用。通过GPIO,计算机或微控制器可以与外部世界进行交互,例如读取传感器数据或控制外部设备(如LED灯、电机等)。 GPIO的应用场景 按钮和开…...
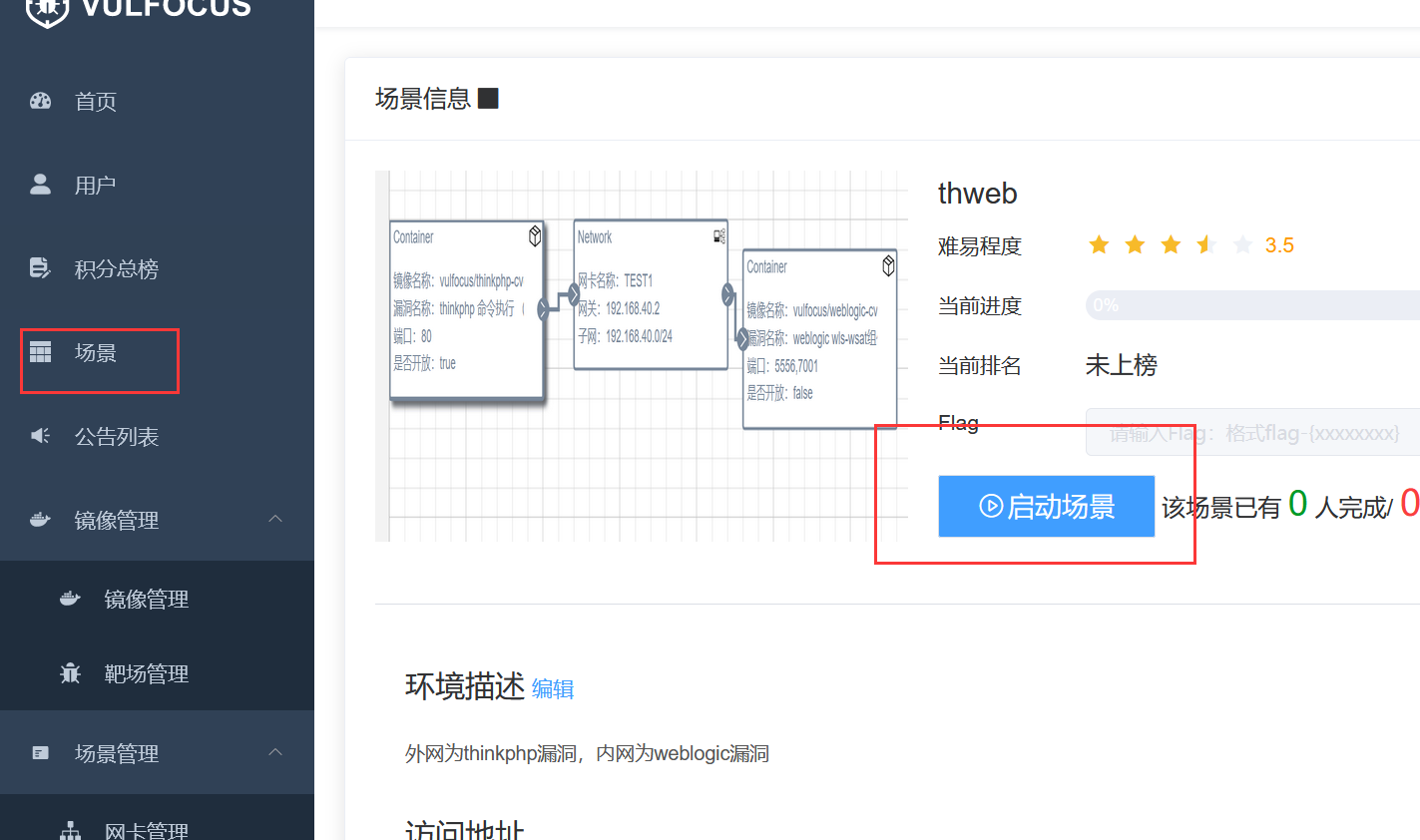
vulfocus靶场搭建
vulfocus靶场搭建 什么是vulfocus搭建教程靶场配置场景靶场编排靶场优化 什么是vulfocus Vulfocus 是一个漏洞集成平台,将漏洞环境 docker 镜像,放入即可使用,开箱即用,我们可以通过搭建该靶场,简单方便地复现一些框架…...

Swift基础知识:30.Swift访问控制
在 Swift 中,访问控制(Access Control)是一种用于限制代码模块对其他代码模块的访问权限的机制。通过访问控制,可以控制代码中各个部分的可见性和可访问性,以便于提高代码的安全性、可维护性和可复用性。 访问级别 S…...
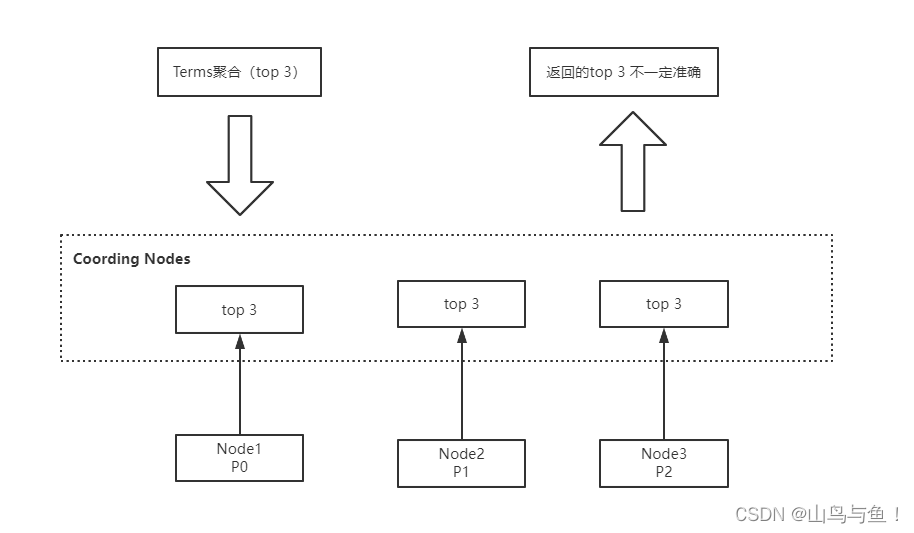
ElasticSearch聚合操作
目录 ElasticSearch聚合操作 基本语法 聚合的分类 后续示例数据 Metric Aggregation Bucket Aggregation ES聚合分析不精准原因分析 提高聚合精确度 ElasticSearch聚合操作 Elasticsearch除搜索以外,提供了针对ES 数据进行统计分析的功能。聚合(aggregation…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
