郑州大学2024年寒假训练 Day7:数论
感觉这一块讲的有点太少了,只有辗转相除法,拓展欧几里得定理,素数筛,快速幂和逆元五个内容。数论的内容远远不止这些。不过一个视频也讲不了太多东西,讲的还是数学,也是没有办法。一边看题一边说吧。
辗转相除法:
辗转相除法又叫欧几里得算法,用来求解两个数的最大公因数(GCD,Greatest Common Divisor)。内容是 g c d ( a , b ) = g c d ( b , a % b ) gcd(a,b)=gcd(b,a\%b) gcd(a,b)=gcd(b,a%b)。中国有一个类似的算法叫做更相减损术,内容是 g c d ( a , b ) = g c d ( a , a − b ) = g c d ( b , a − b ) gcd(a,b)=gcd(a,a-b)=gcd(b,a-b) gcd(a,b)=gcd(a,a−b)=gcd(b,a−b) 其实内容上和欧几里得算法是一个东西。
证明 g c d ( a , b ) = g c d ( b , a % b ) gcd(a,b)=gcd(b,a\%b) gcd(a,b)=gcd(b,a%b):
不妨假设 a > b a>b a>b。设 d = g c d ( a , b ) d=gcd(a,b) d=gcd(a,b) ,那么 a = k 1 ∗ d , b = k 2 ∗ d a=k_1*d,b=k_2*d a=k1∗d,b=k2∗d , 则有 a % b = a − m ∗ b = k 1 ∗ d − m ∗ k 2 ∗ d = ( k 1 − m ∗ k 2 ) ∗ d a\%b=a-m*b=k_1*d-m*k_2*d=(k_1-m*k_2)*d a%b=a−m∗b=k1∗d−m∗k2∗d=(k1−m∗k2)∗d,余数仍然是最大公因数 d d d 的倍数。
还有种证明方法是这样的: a = q ∗ b + r a=q*b+r a=q∗b+r,其中 0 ≤ r < b 0\le r\lt b 0≤r<b,那么 a % b = r a\%b=r a%b=r。因为 a , b a,b a,b 的最大公因数 d d d 可以整除 a , b a,b a,b,即 d ∣ a d|a d∣a 且 d ∣ b d|b d∣b ,所以 d ∣ ( q ∗ b ) d|(q*b) d∣(q∗b),所以 d ∣ ( r = a − q ∗ b ) d|(r=a-q*b) d∣(r=a−q∗b),也就是说明余数 r r r 是 d d d 的倍数。
而 ( a , b ) → ( b , a % b ) (a,b)\rightarrow(b,a\%b) (a,b)→(b,a%b) 是不断减小的,因此这样算下去的话,最终就会得到 a % b = 0 a\%b=0 a%b=0,此时的 a a a 就是最大公因数。这个辗转相除的过程最多不会超过 l o g log log 次,因此求解 g c d gcd gcd 的时间复杂度是 O ( l o g n ) O(logn) O(logn)
代码片段如下:
这里不需要判断ab谁大谁小并交换,因为再调用一次 gcd(b,a%b) 就实现了交换。
int gcd(int a,int b){return (b)?gcd(b,a%b):a;
}
更神秘的写法:
其实就是每次先对a模上b,然后交换ab,b^=a^=b^=实现的其实就是交换功能。
int gcd(int,a,int b){while(b)b^=a^=b^=a%=b;return a;
}
拓展欧几里得定理:
也就是exgcd(Extended gcd)。它主要是用来求解一次线性同余方程。也就是形如 a ∗ x ≡ c ( m o d p ) a*x\equiv c\pmod p a∗x≡c(modp) 求 x x x 的通解问题。这一篇讲的比较好
对这种问题,我们可以稍加转化,得到 a ∗ x + p ∗ y = c a*x+p*y=c a∗x+p∗y=c 的等式,换种写法就是 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c,变成了二元一次方程求通解问题。在解决这个问题之前,我们可以算出 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 问题的通解,然后通过这个算式可以得到我们所求算式的通解。那么怎么求 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 的通解呢。
贝祖定理( B e ˊ z o u t B\'ezout Beˊzout 定理)
内容是 :对任意整数 a , b a,b a,b,存在一对整数 x , y x,y x,y,满足方程 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 。
证明使用归纳法。当 b = 0 b=0 b=0 时, x = 1 , y = 0 x=1,y=0 x=1,y=0 显然是方程的一组解( g c d ( a , 0 ) = a gcd(a,0)=a gcd(a,0)=a)。
当 b > 0 b>0 b>0,设我们知道方程 b ∗ x + ( a % b ) ∗ y = g c d ( b , a % b ) = g c d ( a , b ) b*x+(a\%b)*y=gcd(b,a\%b)=gcd(a,b) b∗x+(a%b)∗y=gcd(b,a%b)=gcd(a,b) 的解,求 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 的解。 b ∗ x + ( a % b ) ∗ y = g c d ( b , a % b ) b*x+(a\%b)*y=gcd(b,a\%b) b∗x+(a%b)∗y=gcd(b,a%b) b ∗ x + ( a − b ∗ ⌊ a b ⌋ ) ∗ y = g c d ( a , b ) b*x+(a-b*\left\lfloor\frac ab\right\rfloor)*y=gcd(a,b) b∗x+(a−b∗⌊ba⌋)∗y=gcd(a,b) a ∗ y + b ∗ x − b ∗ ⌊ a b ⌋ ∗ y = g c d ( a , b ) a*y+b*x-b*\left\lfloor\frac ab\right\rfloor*y=gcd(a,b) a∗y+b∗x−b∗⌊ba⌋∗y=gcd(a,b) a ∗ y + b ∗ ( x − ⌊ a b ⌋ ∗ y ) = g c d ( a , b ) a*y+b*(x-\left\lfloor\frac ab\right\rfloor*y)=gcd(a,b) a∗y+b∗(x−⌊ba⌋∗y)=gcd(a,b)
设 b ∗ x + ( a % b ) ∗ y = g c d ( b , a % b ) b*x+(a\%b)*y=gcd(b,a\%b) b∗x+(a%b)∗y=gcd(b,a%b) 一组特解是 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) ,可以发现, a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 一组可行解就是 x = y 0 , y = x 0 − ⌊ a b ⌋ ∗ y 0 x=y_0,y=x_0-\left\lfloor\frac ab\right\rfloor*y_0 x=y0,y=x0−⌊ba⌋∗y0。我们用辗转相除法向下走到尽头,从最下面的 a ∗ 1 + b ∗ 0 = g c d ( a , 0 ) a*1+b*0=gcd(a,0) a∗1+b∗0=gcd(a,0) 一步一步向上推理,就可以得到原本式子的一组特解。
得到特解后会想得到 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 的通解,这个好说, a ∗ x a*x a∗x 多一个 a ∗ b g c d ( a , b ) \dfrac{a*b}{gcd(a,b)} gcd(a,b)a∗b,那么 b ∗ y b*y b∗y 就少一个 a ∗ b g c d ( a , b ) \dfrac{a*b}{gcd(a,b)} gcd(a,b)a∗b 就行了。也就是说, x x x 每加一个 b g c d ( a , b ) \dfrac{b}{gcd(a,b)} gcd(a,b)b, y y y 就减少一个 a g c d ( a , b ) \dfrac{a}{gcd(a,b)} gcd(a,b)a,可以维持等式不变。写成式子就是,通解 x ‾ = x + k ∗ b g c d ( a , b ) , y ‾ = y − k ∗ a g c d ( a , b ) \overline x=x+k*\dfrac{b}{gcd(a,b)},\overline y=y-k*\dfrac{a}{gcd(a,b)} x=x+k∗gcd(a,b)b,y=y−k∗gcd(a,b)a。令 t 1 = b g c d ( a , b ) t1=\dfrac{b}{gcd(a,b)} t1=gcd(a,b)b,那么就是 x ‾ = x + k ∗ t 1 \overline x=x+k*t1 x=x+k∗t1,这相当于通解模 t 1 t1 t1 同余特解,即 x ‾ ≡ x ( m o d t 1 ) \overline x\equiv x\pmod{t1} x≡x(modt1),因此求 x x x 的最小非负整数解就是 ( x % t 1 + t 1 ) % t 1 (x\%t1+t1)\%t1 (x%t1+t1)%t1,同理 y y y 的通解。
代码片段如下:
int exgcd(int a,int b,int &x,int &y){if(!b){x=1;y=0;return a;}int d=exgcd(b,a%b,x,y);int z=x;x=y;y=z-(a/b)*y;return d;
}
压行:
int exgcd(int a,int b,int &x,int &y){if(!b){x=1;y=0;return a;}int d=exgcd(b,a%b,y,x);//这里相当于交换了xy的值y-=a/b*x;return d;
}
另外提一嘴,对任意一个方程 a ∗ x + b ∗ y = d = g c d ( a , b ) a*x+b*y=d=gcd(a,b) a∗x+b∗y=d=gcd(a,b) ,等式两边同时除以最大公因数 d d d,就得到了 a d ∗ x + b d ∗ y = 1 \dfrac ad*x+\dfrac bd*y=1 da∗x+db∗y=1 ,解和上面是一样的。也就是说当 a , b a,b a,b 互质时 a ∗ x + b ∗ y = 1 a*x+b*y=1 a∗x+b∗y=1 一定有解。反之也成立(不然你 a , b a,b a,b 都是 d d d 的倍数, x , y x,y x,y 是整数,它们乘积的和也一定是 d d d 的倍数,但是 1 1 1 不包含任何大于1的因数,因此 a , b a,b a,b 不可能同时是任何一个 d d d 的倍数)。
拓展欧几里得值域分析:
因为在这里面无法取模,否则会导致出错,所以会担心运算过程中出现超大的数导致溢出。不过安心,所有x和y的中间值的绝对值都小于 ∣ m a x { a , b } ∣ |max\{a,b\}| ∣max{a,b}∣。证明还是数学归纳法。详细的证明步骤在上面给出的博客中详细证明了。不多赘述。
裴蜀定理
内容:设 a , b a,b a,b 为正整数,则关于 a , b a,b a,b 的方程 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c 有整数解当且仅当 c c c 是 g c d ( a , b ) gcd(a,b) gcd(a,b) 的倍数。
也就是说如果 c c c 不能被 g c d ( a , b ) gcd(a,b) gcd(a,b) 整除,方程无整数解,否则有整数解。不证明了。
我们通过上面的方式得到了 a ∗ x + b ∗ y = g c d ( a , b ) a*x+b*y=gcd(a,b) a∗x+b∗y=gcd(a,b) 一组特解,现在要得到 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c 通解。先算特解,再找到通解的之间的变化量即可。这个好说,假设 c = k ∗ d c=k*d c=k∗d ,那么在等式 a ∗ x + b ∗ y = d = g c d ( a , b ) a*x+b*y=d=gcd(a,b) a∗x+b∗y=d=gcd(a,b) 两边同时乘以 k = c d k=\dfrac cd k=dc 就完事了,式子就变成了 a ∗ ( c d ⋅ x ) + b ∗ ( c d ⋅ y ) = c a*(\dfrac cd\cdot x)+b*(\dfrac cd\cdot y)=c a∗(dc⋅x)+b∗(dc⋅y)=c。新的特解就是 x = c d ⋅ x , y = c d ⋅ y x=\dfrac cd\cdot x,y=\dfrac cd\cdot y x=dc⋅x,y=dc⋅y。不过由于系数没变,所以变化量是不变的,还是 t 1 = b d , t 2 = a d t1=\dfrac bd,t2=\dfrac ad t1=db,t2=da。
总结,通过拓展欧几里得算法可以算出等式 a ∗ x + b ∗ y = d = g c d ( a , b ) a*x+b*y=d=gcd(a,b) a∗x+b∗y=d=gcd(a,b) 一组特解 x 0 , y 0 x_0,y_0 x0,y0,那么等式 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c 一组特解是 x = c / d ∗ x 0 , y 0 = c / d ∗ y 0 x=c/d*x_0,y_0=c/d*y_0 x=c/d∗x0,y0=c/d∗y0,通解 x ‾ \overline x x 的变化量是 t 1 = b / d t1=b/d t1=b/d,通解 y ‾ \overline y y 的变化量是 t 2 = a / d t2=a/d t2=a/d。等式 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c 的通解为 x ‾ = x + k ∗ t 1 , y ‾ = y − k ∗ t 2 \overline x=x+k*t1,\overline y=y-k*t2 x=x+k∗t1,y=y−k∗t2
素数筛
试除法(开方暴力)
我们想要知道一个数 x x x 是不是素数,朴素的想法是枚举 2 ∼ x − 1 2\sim x-1 2∼x−1 ,暴力地尝试 x x x 能不能被其中一个整除。这样是 O ( n ) O(n) O(n) 的。一个显而易见的性质是,如果一个数 x x x 是合数,那么它一定存在一个质因数 p p p,而且 2 ≤ p ≤ x 2\le p \le \sqrt x 2≤p≤x。
反证法证明:假设合数 x x x 最小质因数为 p p p,如果上述性质不满足条件,说明 p > x p>\sqrt x p>x,因为 x x x 为合数,因此 x x x 存在至少一个另一个质因数 q q q,根据题设 p p p 是最小的质因数,因此 q > = q q>=q q>=q,那么有 p ∗ q ≥ p 2 > ( x ) 2 = x p*q\ge p^2>(\sqrt x)^2=x p∗q≥p2>(x)2=x,两个因数的乘积大于了这个数,矛盾,因此 2 ≤ p ≤ x 2\le p \le \sqrt x 2≤p≤x。
所以我们枚举 2 ∼ ⌊ x ⌋ 2\sim \lfloor\sqrt x\rfloor 2∼⌊x⌋ 就行了,时间复杂度是 O ( n ) O(\sqrt n) O(n)。代码如下:
bool isp(int x){if(x==1)return false;for(int i=2;i*i<=x;i++)if(x%i==0)return false;return true;
}
埃式筛
我们从 2 2 2 往后看每个数,如果这个数是质数,直接去标记一下它所有的倍数,这样就可以把有这个质因数的合数标记掉。如果一个数是合数,那么它一定存在小于它的质因子。如果我们对每个遇到的质因数都这样做,那么我们在看到一个合数之前,它一定会被标记掉。我们从前往后看到的所有没有标记的数都是素数。所以我们从 1 1 1 到 n n n 走一遍这种操作,就可以得到 1 ∼ n 1\sim n 1∼n 中所有的素数。
这种像筛子一样一次一次把合数筛出来的过程就是埃式筛,它筛数的次数约有: n / 2 + n / 3 + n / 5 + ⋯ + n / p + … ( p 是质数 ) ≤ n / 1 + n / 2 + n / 3 + ⋯ + n / n n/2+n/3+n/5+\dots+n/p+\dots\quad (p是质数)\le n/1+n/2+n/3+\dots+n/n n/2+n/3+n/5+⋯+n/p+…(p是质数)≤n/1+n/2+n/3+⋯+n/n ,当 n → ∞ n\rightarrow\infty n→∞ 时, n / 1 + n / 2 + n / 3 + ⋯ + n / n = n l o g n n/1+n/2+n/3+\dots+n/n=nlogn n/1+n/2+n/3+⋯+n/n=nlogn(这东西学名叫调和级数,想看证明可以搜),因此埃式筛的筛的次数也就是时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),而且是常数很小的 n l o g n nlogn nlogn。代码如下:
bool vis[maxn];
void eratosthenes(int n){vis[1]=true;for(int i=2;i<=n;i++){if(!vis[i])for(int j=2*i;j<=n;j+=i)vis[j]=true;}
}
欧拉筛
上面发现一个合数可能会被筛去多次,有没有办法使得每个数只被筛去一次?有。
我们想要一个合数只被它最小的质因数与和它对应的次大的因数(最大因数就是它本身)筛去。当我们看到一个数的时候,枚举目前已经找到的质数,质数与我们看到的这个数相乘得到的数就是以枚举的质数为最小质因子的数。当我们枚举的质数已经可以整除我们现在看到的这个数的时候,就说明后面的质数不再小于等于我们看到的这个数的最小质因数了,就可以退出了。
通过这种想法,任何一个合数都一定会被它最小的质因数与和它对应的次大的因数筛去一次。所以时间复杂度是 O ( n ) O(n) O(n) 的。代码如下。
int prime[maxn],cnt;
bool vis[maxn];
void Eular(int n){for(int i=2;i<=n;i++){if(!vis[i])prime[++cnt]=i;for(int j=1,p=prime[1];j<=cnt && i*p<=n;p=prime[++j]){vis[i*p]=true;if(i%p==0)break;}}
}
这个筛的过程一定要融会贯通,因为它每个筛到的数都一定是这个数最小的质因数来筛,这个性质很强,所以对这个东西略微修改就可以同时处理很多有用的信息。比如每个数的最小质因数,每个数所有的质因数,计算欧拉函数,莫比乌斯函数等等。
快速幂
普通算 a b a^b ab 的方式就是把 b b b 个 a a a 乘起来,时间复杂度是 O ( b ) O(b) O(b) 的。
发现一个东西,就是 a ∗ a = a 2 , a 2 ∗ a 2 = a 4 , a 4 ∗ a 4 = a 8 , . . . a*a=a^2,a^2*a^2=a^4,a^4*a^4=a^8,... a∗a=a2,a2∗a2=a4,a4∗a4=a8,... 通过这种方式可以快速算出指数很大的 a a a 的幂,然后我们再用预先算出来的这些幂指数去凑出答案的幂指数就行了。
举个例子,如果我们要算 a 10 a^{10} a10 ,那么我们可以先算出来 a 1 , a 2 , a 4 , a 8 a^1,a^2,a^4,a^8 a1,a2,a4,a8,然后 a 10 = a 2 ∗ a 8 a^{10}=a^2*a^8 a10=a2∗a8。当指数很大的时候,优势就更大了,比如 a 1025 = a 1024 ∗ a 1 a^{1025}=a^{1024}*a^1 a1025=a1024∗a1,而处理到 a 1024 a^{1024} a1024 只需要十次。
其实这东西有点像二进制,我们处理出来的是 a 1 ( 2 ) , a 1 0 ( 2 ) , a 10 0 ( 2 ) , a 100 0 ( 2 ) a^{1_{(2)}},a^{10_{(2)}},a^{100_{(2)}},a^{1000_{(2)}} a1(2),a10(2),a100(2),a1000(2) ,相乘其实就是幂指数相加,通过幂指数相加得到任何一个我们想要的幂指数。比如 a 10 = a 101 0 ( 2 ) = a 100 0 ( 2 ) + 1 0 ( 2 ) = a 100 0 ( 2 ) ∗ a 1 0 ( 2 ) a^{10}=a^{1010_{(2)}}=a^{1000_{(2)}+10_{(2)}}=a^{1000_{(2)}}*a^{10_{(2)}} a10=a1010(2)=a1000(2)+10(2)=a1000(2)∗a10(2)。想要凑出指数为 b b b,二进制位最多 l o g 2 b log_2b log2b 位,所以快速幂的时间复杂度为 O ( l o g 2 b ) O(log_2b) O(log2b)
代码如下:
ll qpow(ll a,ll b,ll mod){ll base=a%mod,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}
逆元
这个东西主要是为了解决模意义下不能相除的问题。那么我们怎么才能实现相除呢?
假设 b b b 在取模意义下相当于 1 a \dfrac 1a a1 或者说 a − 1 a^{-1} a−1,那么有 a ∗ b ≡ 1 ( m o d p ) a*b\equiv1\pmod p a∗b≡1(modp)。
费马小定理:
内容:若 p p p 是质数,且 a a a 不是 p p p 的倍数,则有: a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv1\pmod p ap−1≡1(modp)
它是欧拉定理的一个特例,不过在大部分情况下已经够用。这里要特别注意限定条件必须满足。因为 a p − 1 ≡ 1 ( m o d p ) a^{p-1}\equiv1\pmod p ap−1≡1(modp),所以 a p − 2 ∗ a ≡ 1 ( m o d p ) a^{p-2}*a\equiv1\pmod p ap−2∗a≡1(modp),这里 a p − 2 a^{p-2} ap−2 就实现了上面的 b b b 的功能,因此 a p − 2 ≡ 1 a ( m o d p ) a^{p-2}\equiv \dfrac 1a\pmod p ap−2≡a1(modp)。
简单来说,如果模数是质数 p p p,要除以 a a a,那么就直接乘以 a p − 2 a^{p-2} ap−2 就可以实现相同的作用了。
A - 最大公约数和最小公倍数问题
思路:
如果把 x 0 , y 0 x_0,y_0 x0,y0 质因数分解,就得到了 x 0 = p 1 c 1 ∗ p 2 c 2 ∗ p 3 c 3 ∗ ⋯ ∗ p i c i , y 0 = p 1 t 1 ∗ p 2 t 2 ∗ p 3 t 3 ∗ ⋯ ∗ p j t j x_0=p_1^{c_1}*p_2^{c_2}*p_3^{c_3}*\dots*p_i^{c_i},y_0=p_1^{t_1}*p_2^{t_2}*p_3^{t_3}*\dots*p_j^{t_j} x0=p1c1∗p2c2∗p3c3∗⋯∗pici,y0=p1t1∗p2t2∗p3t3∗⋯∗pjtj,而且 t i ≥ c i t_i\ge c_i ti≥ci。对 P , Q P,Q P,Q 来说,它们肯定都有 x 0 x_0 x0 的质因数部分,而从 x 0 x_0 x0 到 y 0 y_0 y0 的这一块质因数部分完全不重合。也就是说从 y 0 x 0 = p 1 m 1 ∗ p 2 m 2 ∗ p 3 m 3 ∗ ⋯ ∗ p j m j \frac {y_0} {x_0}=p_1^{m_1}*p_2^{m_2}*p_3^{m_3}*\dots*p_j^{m_j} x0y0=p1m1∗p2m2∗p3m3∗⋯∗pjmj ,取出若干种质因数 p k m k p_k^{m_k} pkmk 分给 P P P,剩下的分给 Q Q Q 就是一个可行的解。(每种质因数只能分给 P , Q P,Q P,Q 其中一个,否则分给 P , Q P,Q P,Q 的部分会出现重合)
因为一种质因数要么分给 P P P,要么分给 Q Q Q,每种质因数有两种选择,如果 y 0 x 0 \frac {y_0} {x_0} x0y0 有 x x x 种质因数,那么分法也就是答案就有 2 x 2^x 2x 种。
code:
#include <iostream>
#include <cstdio>
using namespace std;int x,y;int main(){cin>>x>>y;if(y%x){cout<<0;return 0;}x=y/x;int cnt=0;for(int i=2;i*i<=x;i++)if(x%i==0){cnt++;while(x%i==0)x/=i;}if(x>1)cnt++;cout<<(1ll<<cnt);return 0;
}
B - 二元一次不定方程 (exgcd)
思路:
求解形如 a ∗ x + b ∗ y = c a*x+b*y=c a∗x+b∗y=c 方程的通解已经在上面详细描述过了,这里尝试算出正整数解的个数和 x , y x,y x,y 的最大和最小正整数解。
假设我们已经算到了 x ‾ = x + k ∗ t 1 , y ‾ = y − k ∗ t 2 \overline x=x+k*t1,\overline y=y-k*t2 x=x+k∗t1,y=y−k∗t2。 x , y x,y x,y 的最小正整数解好算,先看 x x x ,因为是正整数解,不是非负整数解,不包括0,解的值域应该是 [ 1 , t 1 ] [1,t1] [1,t1],所以我们的计算式应该是 x m i n = ( ( x − 1 ) % t 1 + t 1 ) % t 1 + 1 x_{min}=((x-1)\%t1+t1)\%t1+1 xmin=((x−1)%t1+t1)%t1+1,同理 y m i n = ( ( y − 1 ) % t 2 + t 2 ) % t 2 + 1 y_{min}=((y-1)\%t2+t2)\%t2+1 ymin=((y−1)%t2+t2)%t2+1。
而 x x x 取到最大正整数解时, y y y 此时应该正好取到最小正整数解,因此我们把 y m i n y_{min} ymin 代入,算出此时的 x x x 即可。同理 y y y。
正整数解的个数其实就看一个变量就可以了。比如看 x x x ,其实就是 x m i n x_{min} xmin 和 x m a x x_{max} xmax 中间差了几个 t 1 t1 t1 。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;ll T,a,b,c;ll exgcd(ll a,ll b,ll &x,ll &y){if(!b){x=1;y=0;return a;}ll d=exgcd(b,a%b,x,y);ll z=x;x=y;y=z-(a/b)*y;return d;
}int main(){cin>>T;while(T--){scanf("%lld%lld%lld",&a,&b,&c);ll x,y,d=exgcd(a,b,x,y);if(c%d){printf("-1\n");continue;}x=c/d*x;y=c/d*y;ll t1=b/d,t2=a/d;ll xmi=((x-1)%t1+t1)%t1+1,ymi=((y-1)%t2+t2)%t2+1,xmx,ymx;xmx=(c-ymi*b)/a;ymx=(c-xmi*a)/b;if(xmx<=0 || ymx<=0){printf("%lld %lld\n",xmi,ymi);}else {printf("%lld %lld %lld %lld %lld\n",(xmx-xmi)/t1+1,xmi,ymi,xmx,ymx);}}return 0;
}
C - 质因数分解
思路:
枚举所有可能的因数,得到的第一个因数对应的另一个因数就是答案。
根据上面提到的性质,如果一个数 x x x 是合数,那么它一定存在一个质因数 p p p,而且 2 ≤ p ≤ x 2\le p \le \sqrt x 2≤p≤x。我们最多找到 x \sqrt x x 就能找到答案了。
code:
#include <iostream>
#include <cstdio>
using namespace std;int n;int main(){cin>>n;for(int i=2;i*i<=n;i++)if(n%i==0){cout<<n/i;return 0;}return 0;
}
D - 质数筛
思路:
写作素数筛,读作开方暴力,直接暴力验证每个数是不是质数就行了。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=105;int n,a[maxn];bool isp(int x){if(x==1)return false;for(int i=2;i*i<=x;i++)if(x%i==0)return false;return true;
}int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++)if(isp(a[i]))cout<<a[i]<<" ";return 0;
}
E - Prime Distance
题意:
给你两个数 L , U L,U L,U , 1 ≤ L < U ≤ 2147483647 1\le L< U\le 2147483647 1≤L<U≤2147483647 且 U − L ≤ 1000000 U-L\le 1000000 U−L≤1000000 。问 L ∼ U L\sim U L∼U 中相邻的两个质数中差值最小和最大的一对质数是什么。
思路:
直接跑筛法是跑不动的,但是根据一个数 x x x 如果是合数,那么一定存在一个小于等于 x \sqrt x x 的质因数的性质可以知道, L ∼ U L\sim U L∼U 中的所有合数最大的最小质因数不会超过 U \sqrt U U ,我们直接预处理处理 U \sqrt U U 以内的所有素数,然后对每个素数筛掉 L ∼ U L\sim U L∼U 中它的倍数, L ∼ U L\sim U L∼U 中剩下的没有被筛掉的数就是素数。
需要注意当 L = 1 L=1 L=1 时,会有一个 1 1 1 不会被筛掉,而它既不是素数也不是合数,因此需要特判去除。
code:
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn=1e5+5;
typedef long long ll;
const ll inf=1e18;ll L,U;int prime[maxn],cnt;
bool tvis[maxn*50];
void Eular(int n){tvis[1]=true;for(int i=2;cnt<=n;i++){if(!tvis[i])prime[++cnt]=i;for(int j=1,p=prime[1];j<=cnt && i*p<maxn*50;p=prime[++j]){tvis[i*p]=true;if(i%p==0)break;}}
}int main(){Eular(1e5);while(cin>>L>>U){vector<bool> vis(U-L+5);if(L==1)vis[0]=true;for(ll i=1,p=prime[1];i<=cnt && p*p<=U;p=prime[++i])for(ll j=max((L+p-1)/p,2ll);j*p<=U;j++)vis[j*p-L]=true;ll dmi=inf,dmx=0,l1,r1,l2,r2;for(ll i=0,lst=-1;i<=U-L;i++){if(!vis[i]){if(~lst){if(i-lst<dmi){dmi=i-lst;l1=lst;r1=i;}if(i-lst>dmx){dmx=i-lst;l2=lst;r2=i;}lst=i;}else lst=i;}}if(dmx)printf("%lld,%lld are closest, %lld,%lld are most distant.\n",L+l1,L+r1,L+l2,L+r2);else printf("There are no adjacent primes.\n");}return 0;
}
F - 线性筛素数
思路:
素数筛板子, p r i m e prime prime 数组中记录的就是从 1 ∼ n 1\sim n 1∼n 的所有素数, p r i m e [ k ] prime[k] prime[k] 就是第 k k k 大的素数。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e7+5;int n,q;int prime[maxn],cnt;
bool vis[maxn*10];
void Eular(int n){for(int i=2;i<=n;i++){if(!vis[i])prime[++cnt]=i;for(int j=1,p=prime[1];j<=cnt && i*p<=n;p=prime[++j]){vis[i*p]=true;if(i%p==0)break;}}
}int main(){cin>>n>>q;Eular(n);for(int i=1,k;i<=q;i++){cin>>k;cout<<prime[k]<<endl;}return 0;
}
G - 又是毕业季II
思路:
好题。洛谷 P1414 又是毕业季II看不懂可以去题解区翻题解看
取出 k k k 个数的最大公因数,我们算一遍 看 看 看 个人的最大公因数是 k ∗ l o g k*log k∗log 次数的,再枚举选择数…不用想了,复杂度爆炸。
那怎么得到 k k k 个人的最大公因数。如果我们知道前 k − 1 k-1 k−1 个人的最大公因数,如果第 k k k 个人有因数是这个最大公因数,那么最大公因数不变,否则是更小的需要所有人都有的因数。
嗯?如果我们一开始就对每个数标记一下以它为因数的人有几个不就好了,假设记录数组叫 v i s vis vis。这样处理一下的话,如果我们找 k k k 个人的最大公因数,就直接在 1 ∼ i n f = 1 0 6 1\sim inf=10^6 1∼inf=106 中找最大的 i i i,满足 v i s [ i ] ≥ k vis[i]\ge k vis[i]≥k 即可。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=1e4+5;
const int maxf=1e6+5;int n,vis[maxf];//是i的倍数的有多少个 int ans[maxn];int main(){cin>>n;for(int i=1,t;i<=n;i++){cin>>t;for(int p=1;p*p<=t;p++)if(t%p==0){vis[p]++;if(p*p!=t)vis[t/p]++;}}for(int i=1e6;i>=1;i--)if(!ans[vis[i]])ans[vis[i]]=i;for(int i=n,mx;i>=1;i--){mx=max(mx,ans[i]);ans[i]=mx;}for(int i=1;i<=n;i++)cout<<ans[i]<<endl;return 0;
}
H - 快速幂
思路:
快速幂板题
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;ll a,b,p;ll qpow(ll a,ll b,ll mod){ll base=a%mod,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}int main(){cin>>a>>b>>p;printf("%lld^%lld mod %lld=%lld\n",a,b,p,qpow(a,b,p));return 0;
}
I - Carmichael Numbers
题意:
Alvaro 认为,与传统海鲜饭相比,加密海鲜饭的主要优势在于,除了你自己,没人知道你吃的是什么。
一个合数如果能够通过费马素性检验: a n m o d n = a a^n\ mod\ n=a an mod n=a就认为他是个一个 C a r m i c h a e l n u m b e r Carmichael\ number Carmichael number。
现在给你一个数,问你它是不是 C a r m i c h a e l n u m b e r Carmichael\ number Carmichael number
思路:
可以先把合数筛出来。如果给的是合数,再进行一下费马素性检验,如果都能通过就输出 C a r m i c h a e l n u m b e r Carmichael\ number Carmichael number。
code:
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=65005;int n;int prime[maxn],cnt;
bool vis[maxn];
void Eular(int n){vis[1]=true;for(int i=2;i<=n;i++){if(!vis[i])prime[++cnt]=i;for(int j=1,p=prime[1];j<=cnt && i*p<=n;p=prime[++j]){vis[i*p]=true;if(i%p==0)break;}}
}ll qpow(ll a,ll b,ll mod){ll base=a%mod,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}int main(){Eular(65000);while(cin>>n,n){if(!vis[n]){printf("%d is normal.\n",n);continue;}bool f=true;for(int i=2;i<n;i++){if(qpow(i,n,n)!=i){f=false;//不满足素性检验 break;}}if(f)printf("The number %d is a Carmichael number.\n",n);else printf("%d is normal.\n",n);}return 0;
}
J - 因子和
思路:
洛谷 P1593 因子和
首先需要知道一个数 a a a 的所有因数和是多少。把 a a a 质因数分解,得到 a = p 1 c 1 ∗ p 2 c 2 ∗ p 3 c 3 ∗ ⋯ ∗ p m c m a=p_1^{c_1}*p_2^{c_2}*p_3^{c_3}*\dots*p_m^{c_m} a=p1c1∗p2c2∗p3c3∗⋯∗pmcm 那么它的所有因数的和就是 s u m = ( 1 + p 1 + p 1 2 + ⋯ + p 1 c 1 ) ⋅ ( 1 + p 2 + p 2 2 + ⋯ + p 2 c 2 ) ⋅ ⋯ ⋅ ( 1 + p m + p m 2 + ⋯ + p m c m ) sum=(1+p_1+p_1^2+\dots+p_1^{c_1})\cdot(1+p_2+p_2^2+\dots+p_2^{c_2})\cdot\\\dots\cdot (1+p_m+p_m^2+\dots+p_m^{c_m}) sum=(1+p1+p12+⋯+p1c1)⋅(1+p2+p22+⋯+p2c2)⋅⋯⋅(1+pm+pm2+⋯+pmcm)
这个式子可以这样理解:我们从第一个括号里随便取一项,和第二个括号里随便取一项,以此类推,一直取到最后一个括号,这样就可以得到一个因数。因数一共有 ∏ i = 1 m ( c i + 1 ) \prod_{i=1}^{m}(c_i+1) ∏i=1m(ci+1) 项,也正好是这些选取方案,取法和因数一一对应。
那么 a b a^b ab 的因数和就是: s u m = ( 1 + p 1 + p 1 2 + ⋯ + p 1 c 1 + ⋯ + p 1 b ∗ c 1 ) ⋅ ( 1 + p 2 + p 2 2 + ⋯ + p 2 b ∗ c 2 ) ⋅ ⋯ ⋅ ( 1 + p m + p m 2 + ⋯ + p m b ∗ c m ) sum=(1+p_1+p_1^2+\dots+p_1^{c_1}+\dots+p_1^{b*c_1})\cdot(1+p_2+p_2^2+\dots+p_2^{b*c_2})\cdot\\\dots\cdot (1+p_m+p_m^2+\dots+p_m^{b*c_m}) sum=(1+p1+p12+⋯+p1c1+⋯+p1b∗c1)⋅(1+p2+p22+⋯+p2b∗c2)⋅⋯⋅(1+pm+pm2+⋯+pmb∗cm)
第一个括号内是一个等比数列,首项为1,公比为 p 1 p_1 p1。因此第一个括号内的内容的总和 = 1 ∗ ( 1 − p 1 b ∗ c 1 + 1 ) 1 − p 1 = p 1 b ∗ c 1 + 1 − 1 p 1 − 1 =\dfrac {1*(1-p_1^{b*c_1+1})}{1-p_1}=\dfrac {p_1^{b*c_1+1}-1}{p_1-1} =1−p11∗(1−p1b∗c1+1)=p1−1p1b∗c1+1−1。对 p 1 b ∗ c 1 + 1 p_1^{b*c_1+1} p1b∗c1+1 求快速幂,对 p 1 − 1 p_1-1 p1−1 算逆元就能快速求解了,对一个数,处理出它所有的质因数和对应个数,每个质因数用这个过程算出答案,结果累乘起来即可。
不过 p 1 − 1 p_1-1 p1−1 可以计算逆元的前提条件是 p 1 − 1 ≢ 0 ( m o d 9901 ) p_1-1\not\equiv0\pmod {9901} p1−1≡0(mod9901),因此当 p 1 ≡ 1 ( m o d 9901 ) p_1\equiv1\pmod {9901} p1≡1(mod9901) 时的情况单独处理,发现原式子中这个数就等于 b ∗ c 1 + 1 b*c_1+1 b∗c1+1 。
注意 a = 0 a=0 a=0 的情况需要特判。
code:
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
const ll mod=9901;
#define pii pair<int,int>ll a,b;
vector<pii> t;ll qpow(ll a,ll b){b%=mod-1;ll base=a%mod,ans=1;while(b){if(b&1){ans*=base;ans%=mod;}base*=base;base%=mod;b>>=1;}return ans;
}
ll inv(ll x){return qpow(x,mod-2);}int main(){cin>>a>>b;if(a==0){cout<<0<<endl;return 0;}for(int i=2,cnt;i*i<=a;i++){if(a%i==0){cnt=0;while(a%i==0){a/=i;cnt++;}t.push_back(pii(i,cnt));}}if(a>1)t.push_back(pii(a,1));ll ans=1;for(auto x:t){ll p=x.first,c=x.second;if(p%mod!=1)ans=ans*(qpow(p%mod,b*c+1)-1)%mod*inv(p-1)%mod;else ans=ans*(b*c+1)%mod;}cout<<(ans%mod+mod)%mod;return 0;
}
相关文章:

郑州大学2024年寒假训练 Day7:数论
感觉这一块讲的有点太少了,只有辗转相除法,拓展欧几里得定理,素数筛,快速幂和逆元五个内容。数论的内容远远不止这些。不过一个视频也讲不了太多东西,讲的还是数学,也是没有办法。一边看题一边说吧。 辗转…...
“目标检测”任务基础认识
“目标检测”任务基础认识 1.目标检测初识 目标检测任务关注的是图片中特定目标物体的位置。 目标检测最终目的:检测在一个窗口中是否有物体。 eg:以猫脸检测举例,当给出一张图片时,我们需要框出猫脸的位置并给出猫脸的大小,如…...
springboot+vue的宠物咖啡馆平台(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
LaWGPT—基于中文法律知识的大模型
文章目录 LaWGPT:基于中文法律知识的大语言模型数据构建模型及训练步骤两个阶段二次训练流程指令精调步骤计算资源 项目结构模型部署及推理 LawGPT_zh:中文法律大模型(獬豸)数据构建知识问答模型推理训练步骤 LaWGPT:基…...

一文弄明白KeyedProcessFunction函数
引言 KeyedProcessFunction是Flink用于处理KeyedStream的数据集合,它比ProcessFunction拥有更多特性,例如状态处理和定时器功能等。接下来就一起来了解下这个函数吧 正文 了解一个函数怎么用最权威的地方就是 官方文档 以及注解,KeyedProc…...
alibabacloud学习笔记06(小滴课堂)
讲Sentinel流量控制详细操作 基于并发线程进行限流配置实操 在浏览器打开快速刷新会报错 基于并发线程进行限流配置实操 讲解 微服务高可用利器Sentinel熔断降级规则 讲解服务调用常见的熔断状态和恢复 讲解服务调用熔断例子 我们写一个带异常的接口:...

Code Composer Studio (CCS) - Licensing Information
Code Composer Studio [CCS] - Licensing Information 1. Help -> Code Composer Studio Licensing Information2. Upgrade3. Specify a license fileReferences 1. Help -> Code Composer Studio Licensing Information 2. Upgrade 3. Specify a license file …...

uniapp引入微信小程序直播组件
方法1.小程序跳转视频号直播 微信小程序跳转到视频号 1.1微信开放平台注册 https://open.weixin.qq.com/ 2.2 方法2.使用小程序提供的直播组件 参考 微信小程序跳转视频号直播 小程序直播官方文档 https://developers.weixin.qq.com/miniprogram/dev/component/live-play…...

五个简单的C#编程案例
案例一:Hello, World! csharp using System; class Program { static void Main() { Console.WriteLine("Hello, World!"); } } 这个案例是最基础的C#程序,它打印出“Hello, World!”到控制台。每个C#程…...

Zlibrary低调官宣2024年最新网址,国内可直接访问,免费下载海量电子书籍
最近过节,文章也没怎么写,明天要上班了,今天写篇文章做个预热。 春节期间,“知识大航海”群里,有位群友分享了一个Zlibrary的最新地址,感谢这位群友妹妹的热心分享,这个地址国内可以直接访问。 …...

Android 开机启动
一、添加权限 <uses-permission android:name"android.permission.RECEIVE_BOOT_COMPLETED"/> 二、写一个广播接收器 public class BootReceiver extends BroadcastReceiver {Overridepublic void onReceive(Context context, Intent intent) {if(Intent.ACT…...

二叉树相关算法需了解汇总-基础算法操作
文章目录 144.二叉树的前序遍历145.二叉树的后序遍历94.二叉树的中序遍历102.二叉树的层序遍历107.二叉树的层次遍历倒序199.二叉树的右视图637.二叉树的层平均值429.N叉树的层序遍历515.在每个树行中找最大值116.填充每个节点的下一个右侧节点指针104.二叉树的最大深度111.二叉…...
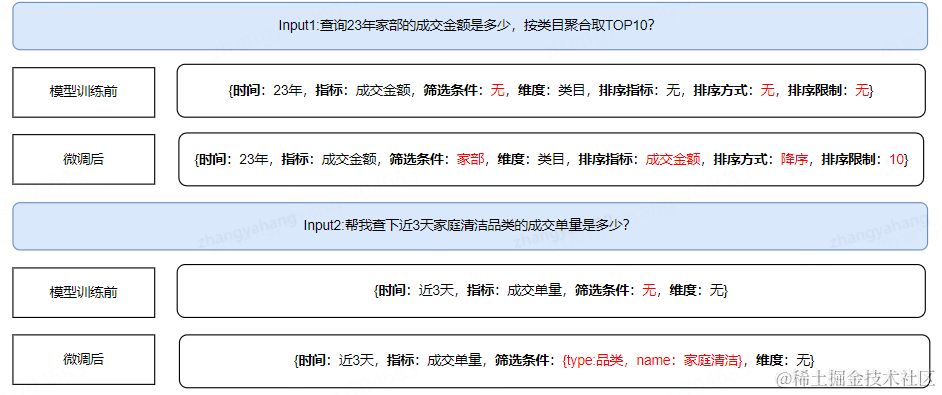
万字干货-京东零售数据资产能力升级与实践
开篇 京东自营和商家自运营模式,以及伴随的多种运营视角、多种组合计算、多种销售属性等数据维度,相较于行业同等量级,数据处理的难度与复杂度都显著增加。如何从海量的数据模型与数据指标中提升检索数据的效率,降低数据存算的成…...

探索前端框架的世界:一场前端之旅
在网络世界中,网页开发领域的一颗明星是前端框架。这些框架为开发者提供了丰富的工具和技术,帮助他们构建出漂亮、高效的网页应用。现在,让我们随着小明的故事一起来探索一下吧。 小明的梦想 小明是一位年轻有为的前端开发者,他…...

class complex
class complex from C_OOP_base1_houjie complex.h #ifndef __COMPLEX__ // 防卫式声明 guard; 名称自定义 #define __COMPLEX__// 0. forward declarations class complex;complex& __doapl (complex* ths, const complex& r);// 1. class declarations class compl…...

数据库系统概论整理与总结
数据库系统概论 第一章:绪论 四个基本概念 四个概念 数据:Data 数据库:DataBase 数据库管理系统:DBMS 数据库系统:DBS 打个比喻,比如说菜鸟物流: Data:快递 DB:物流厂库 DBMS:对…...
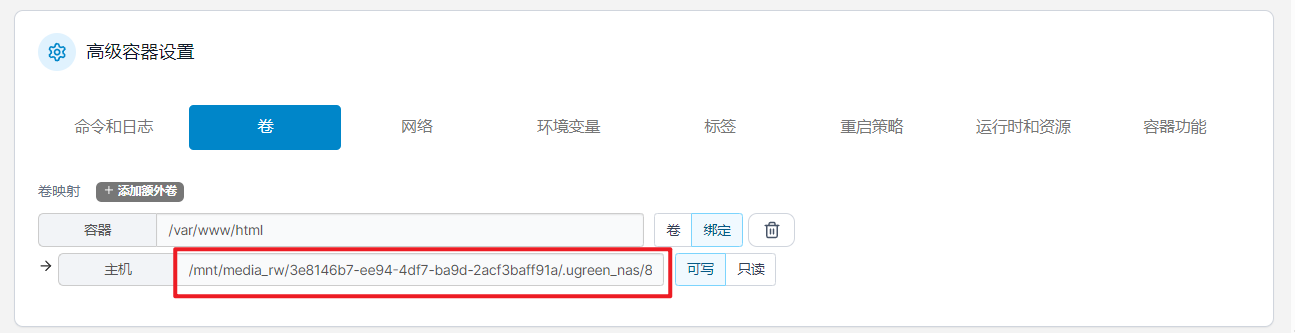
打通新势力NAS权限壁垒,绿联私有云安装Portainer,实现更强大的Docker功能
打通新势力NAS权限壁垒,绿联私有云安装Portainer,实现更强大的Docker功能 对于国产新势力NAS来说,因为安全问题并没有完全开放SSH权限,所以还不能和传统NAS那样直接通过Docker run命令来部署容器,同时,对于…...
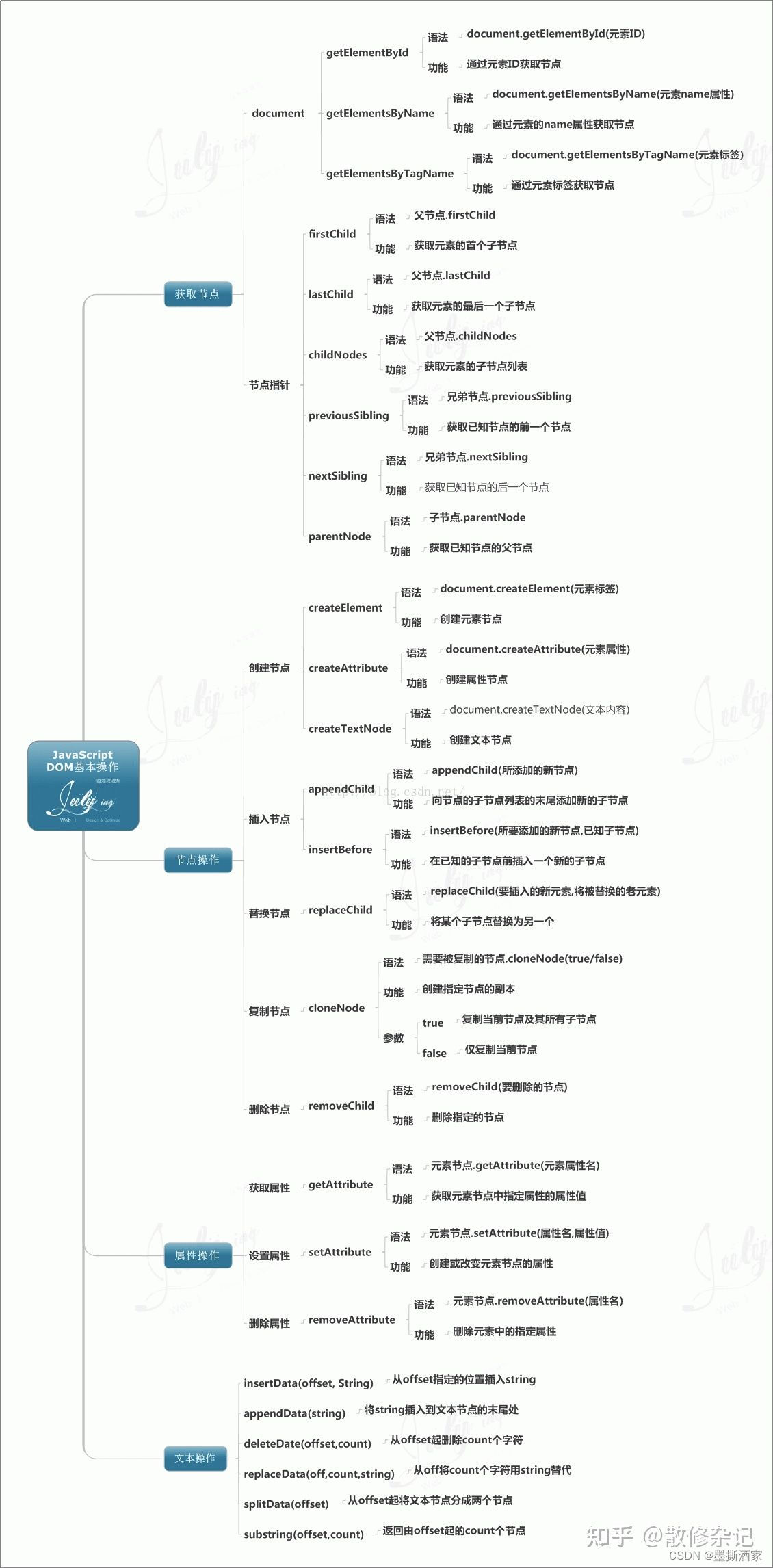
前端基础自学整理|DOM树
DOM,文档对象模型(Document Object Model),简单的说,DOM是一种理念,一种思想,一个与系统平台和编程语言无关的接口,一种方法, 使 Web开发人员可以访问HTML元素!不是具体方…...

RedisDesktopManager无法远程连接到Linux虚拟机中Redis的docker容器的一种解决方案
1.问题描述 除了RedisDesktopManager以外,使用java代码也无法连接到centos7虚拟机中的docker容器中的Redis ,按照网上其他博主的解决方案,在排除Linux防火墙问题,端口映射问题,redis.conf配置文件问题以后,…...

HarmonyOS 权限 介绍
权限说明 权限等级 根据权限对于不同等级应用有不同的开放范围,权限类型对应分为以下三种,等级依次提高。 normal权限 normal 权限允许应用访问超出默认规则外的普通系统资源。 这些系统资源的开放(包括数据和功能)对用户隐私以及…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
