十大基础排序算法
排序算法分类
排序:将一组对象按照某种逻辑顺序重新排列的过程。
-
按照待排序数据的规模分为:
- 内部排序:数据量不大,全部存在内存中;
- 外部排序:数据量很大,无法一次性全部存在内存中,因此排序中需要访问外存。
-
按照排序是否稳定分为:
- 稳定排序:相等的元素在排序前后的相对位置不变。例如,a等于b,且原序列a在b前,排序后a仍在b前,则为稳定排序。
- 不稳定排序:相等元素在排序前后的相对位置可能发生变化。
-
按照是否需要额外内存分为:
- 原地排序:在排序过程中不申请多余的存储空间,只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
- 非原地排序:需要额外内存空间存储数组副本以辅助排序。
-
按照排序方式分为:
- 比较类排序:通过比较来决定元素间的相对次序。
- 非比较类排序:不通过元素间的比较进行排序。

比较类排序
冒泡排序
冒泡排序是一种典型的交换排序。
算法原理:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。这一步结束后,排在最后的元素会是所有数据中最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
冒泡排序基本代码如下:
void BubbleSort(vector<int>& nums){const int size = nums.size();for(int i = 0; i < size; ++i)for(int j = 0; j < size-i-1; ++j)if(nums[j] > nums[j+1])swap(nums[j], nums[j+1]);
}
性能评价:
- 当
nums[j] == nums[j+1]时,我们并不交换它们。所以冒泡排序是稳定的; - 共循环了(n-1)+(n-2)+…+2+1=n(n-1)/2,所以时间复杂度是O(n^2)。
快速排序
快速排序是从冒泡排序演变而来的,实际上是在冒泡排序基础上的递归分治法。
快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分。
快排也用了分治策略,其本质框架类似二叉树的前序遍历。
其实现代码如下:
void QuickSort(std::vector<int>& nums, int left, int right){if(left >= right){return;}//"治"int i = left;int j = right;while(i < j){while(i < j && nums[j] > nums[left]) --j;while(i < j && nums[i] <= nums[left]) ++i;std::swap(nums[i], nums[j]);}std::swap(nums[i], nums[left]);//“分”QuickSort(nums, left, i - 1);QuickSort(nums, i + 1, right);
}
注意事项
- 如果选取数列的第一个元素为基准元素,则从right所指向的元素开始与基准元素进行比较;如果选取数列的最后一个元素为基准元素,则从left所指向的元素开始与基准元素进行比较。
- 如果选取数列的第一个元素为基准元素,left所指向的元素与基准元素第一次对比时,left下标与基准元素下标相等(即:判断条件中添加等号);如果选取数列的最后一个元素为基准元素,right所指向的元素与基准元素第一次对比时,right下标与基准元素下标相等。
时间复杂度:O(nlogn)
空间复杂度:O(1)
稳定性:不稳定
插入排序
基本思想:将待排序数据看成由已排序和未排序两部分组成。对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法流程:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
其实现代码如下:
void InsertSort(vector<int>& nums){const int size = nums.size();for(int i = 1; i < size; ++i){int curr = nums[i];int j = i - 1;while(j >= 0 && curr < nums[j]){nums[j+1] = nums[j];--j;}nums[j+1] = curr;}
}
性能评价:
- 插入排序是稳定的。
- 时间复杂度为O(n^2)。
希尔排序
在插入排序中,当需要插入的数是较小的数时,后移的次数明显增多,对效率有影响.
希尔排序是对插入排序的优化。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

其实现代码如下:
void ShellSort(std::vector<int>& nums){const int size = nums.size();for(int gap = size / 2; gap > 0; gap /= 2){for(int i = gap; i < size; ++i){int curr = nums[i];int j = i - gap;while(j >= 0 && curr < nums[j]){nums[j+gap] = nums[j];j -= gap;}nums[j+gap] = curr;}}
}
选择排序
基本思想:首先在未排序数据找到最小的数,然后把该最小数放到排序序列的末尾,直到所有数据排序完毕。
其实现代码如下:
void SelectionSort(vector<int>& nums){const int size = nums.size();for(int i = 0; i < size-1; ++i){int minIndex = i;for(int j = i+1; j < size; ++j)if(nums[j] < nums[minIndex])minIndex = j;swap(nums[i], nums[minIndex]);}
}
性能评价:
- 简单选择排序是不稳定排序;
- 无论什么数据进去,它的比较次数都是n(n-1)/2,所以时间复杂度是O(n^2)。
堆排序
首先将等待排序的数组构造成一个大根堆,构造结束后整个数组当中的最大值就是堆顶元素;
然后将堆顶元素与数组末尾元素交换位置,交换结束后数组末尾元素为最大值,剩下其他的待排序的数组个数为n-1个;
将剩余的n-1个数再次构造成一个大根堆,再将堆顶元素与数组第n-1个位置的元素交换位置,重复上述步骤可以最终得到一个有序数组。
其实现代码如下:
//堆调整
void Heapify(std::vector<int>& nums, int index, int heap_size){int parent_index = index;int leftChild_index = 2 * parent_index + 1;while(leftChild_index < heap_size){int maxValue_index = leftChild_index+1 < heap_size && nums[leftChild_index+1] > nums[leftChild_index] ? leftChild_index+1 : leftChild_index;maxValue_index = nums[maxValue_index] > nums[parent_index] ? maxValue_index : parent_index;if(maxValue_index == parent_index)return;std::swap(nums[maxValue_index], nums[parent_index]);parent_index = maxValue_index;leftChild_index = 2 * parent_index + 1;}
}
//堆排序
void HeapSort(std::vector<int>& nums){if(nums.size() < 2)return;int heap_size = nums.size();//从下标最大的父节点开始。(最后一个元素的下标是n-1,最后一个父节点的下标是n/2-1)for(int i = heap_size/2 - 1; i >= 0; --i)Heapify(nums, i, heap_size);std::swap(nums[0], nums[--heap_size]);while(heap_size > 0){Heapify(nums, 0, heap_size);std::swap(nums[0], nums[--heap_size]);}
}
时间复杂度:O(nlogn)
空间复杂度:O(1)
稳定性:不稳定
归并排序
简单归并排序即二路归并排序。
归并排序采用分治策略,其本质框架类似二叉树的后序遍历,左右子树的递归就是“分”,根结点的处理部分就是“治”。

其实现代码如下:
std::vector<int> temp;
void MergeSort(std::vector<int>& nums, int left, int right){if(left >= right){return;}int mid = left + (right - left) / 2;//“分”MergeSort(nums, left, mid);MergeSort(nums, mid + 1, right);//"治"int i = left;int j = mid + 1;int t = left;while(i <= mid && j <= right){if(nums[i] <= nums[j]){temp[t++] = nums[i++];}else{temp[t++] = nums[j++];}}while(i <= mid){temp[t++] = nums[i++];}while(j <= right){temp[t++] = nums[j++];}for(int k = left; k <= right; ++k){nums[k] = temp[k];}
}
时间复杂度:O(nlogn)
空间复杂度:O(n)
稳定性:稳定
非比较类排序
基数排序
计数排序
桶排序
总结

不稳定排序记忆口诀:一堆(堆排序)作业,心态不稳,快(快速排序)选择(选择排序)一些(希尔排序)朋友出去玩。
相关文章:

十大基础排序算法
排序算法分类 排序:将一组对象按照某种逻辑顺序重新排列的过程。 按照待排序数据的规模分为: 内部排序:数据量不大,全部存在内存中;外部排序:数据量很大,无法一次性全部存在内存中,…...
IP协议及相关技术协议
一、IP基本认识 1. IP的作用 IP在TCP/IP模型中处于网络层,网络层的主要作用是实现主机与主机之间的通信,而IP的作用是在复杂的网络环境中将数据包发送给最终目的主机。 2. IP与MAC的关系 简单而言,MAC的作用是实现“直连”的两个设备之通信…...

小红书x-s算法及补环境 单旋转验证码
前言 大家好呀!新的一年,先祝大家新年快乐咯.祝大家逆向,风控都一把过咯. 新年第一篇文章,后续会持续更新哦! 春晚见证了中国经济的新风口,今年春晚互联网企业赞助商就两家,小红书和京东.小红书类似国外的ins,有预感未来小红书会大火,所以写了这篇文章,有需要的加我,联系方式…...
代码检测规范和git提交规范
摘要:之前开发的项目,代码检测和提交规范都是已经配置好的,最近自己新建的项目就记录下相关配置过程。 1. ESlint配置 2013年6月创建开源项目,提供一个插件化的JavaScript代码检测工具,创建项目是生成的eslintrc.js文…...
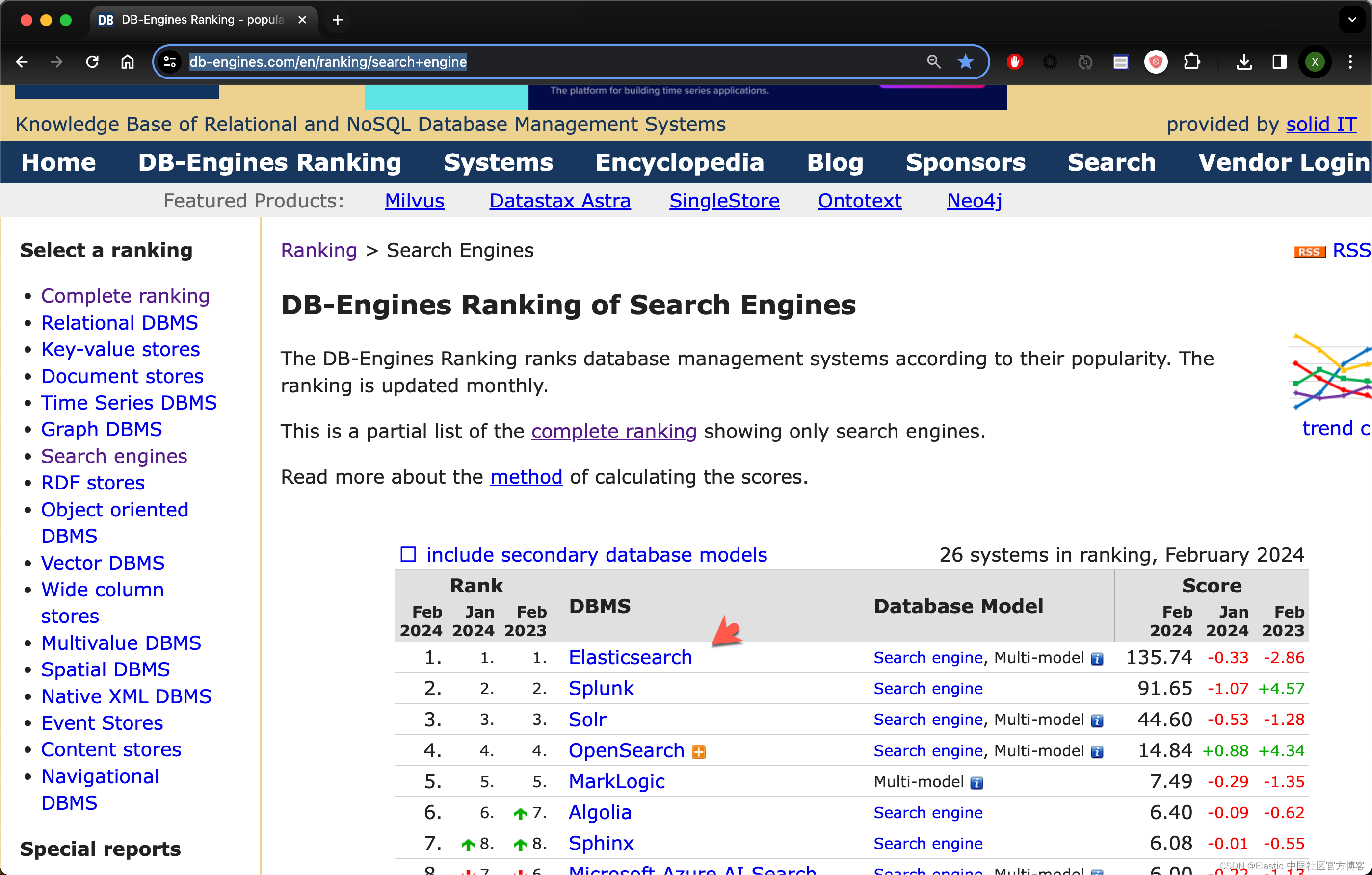
Elasticsearch:什么是搜索引擎?
搜索引擎定义 搜索引擎是一种软件程序或系统,旨在帮助用户查找存储在互联网或特定数据库中的信息。 搜索引擎的工作原理是对各种来源的内容进行索引和编目,然后根据用户的搜索查询向用户提供相关结果列表。 搜索引擎对于希望快速有效地查找特定信息的用…...

人工智能几个关键节点:深蓝,AlphaGo,ChatGPT,Sora
近30年,人工智能几个关键节点:深蓝,AlphaGo,ChatGPT,Sora 深蓝: 1997年,深蓝击败卡斯帕罗夫的比赛是通过一系列复杂的算法和策略实现的。深蓝的开发团队使用了一种名为“暴力搜索”的技术&…...

WordPres Bricks Builder 前台RCE漏洞复现(CVE-2024-25600)
0x01 产品简介 Bricks Builder是一款用于WordPress的开发主题,提供直观的拖放界面,用于设计和构建WordPress网站。它使用户能够轻松创建自定义的网页布局和设计,无需编写或了解复杂的代码。Bricks Builder具有用户友好的界面和强大的功能,使用户可以通过简单的拖放操作添加…...

代码随想录算法训练营总结 | 慢慢总结,想起啥就先写上
二叉树总结 二叉树的结构 stauct TreeNode {int val;TreeNode* left;TreeNode* right; }二叉树的递归函数分析 二叉树的递归函数当做只有一个根节点,一个左子树,一个右节点的数去看,这看着是个废话, 其实很重要 回溯…...

基于开源模型对文本和音频进行情感分析
应用场景 从商品详情页爬取商品评论,对其做舆情分析;电话客服,对音频进行分析,做舆情分析; 通过开发相应的服务接口,进一步工程化; 模型选用 文本,选用了通义实验室fine-tune的st…...

SQL中为什么不要使用1=1
最近看几个老项目的SQL条件中使用了11,想想自己也曾经这样写过,略有感触,特别拿出来说道说道。 编写SQL语句就像炒菜,每一种调料的使用都可能会影响菜品的最终味道,每一个SQL条件的加入也可能会影响查询的执行效率。那…...

python 几种常见的音频数据读取、保存方式
1. soundfile 库的使用 soundfile库是一个Python库,主要用于读取和写入音频文件。它支持多种音频格式,包括WAV、AIFF、FLAC和OGG等。通过soundfile库,用户可以方便地将numpy数组存储到音频文件或者将音频文件加载到numpy数组中。此外&#x…...

关于msvcr120.dll丢失怎样修复的详细解决步骤方法分享,msvcr120.dll文件的相关内容
在电脑使用过程中,我们经常遇到各种系统错误,其中msvcr120.dll丢失是一个常见问题。msvcr120.dll文件是Visual C Redistributable for Visual Studio 2015/2017的一个组件,主要用于支持某些应用程序的正常运行。当电脑出现msvcr120.dll丢失情…...
简单几步通过DD工具把云服务器系统Linux改为windows
简单几部通过DD安装其他系统,当服务器的web控制台没有我们要装的系统,就需要通过DD(Linux磁盘)工具来更改系统,(已知支持KVM系统) 本文如何简单的更换系统,不通过web控制台来更换&a…...

使用 package.json 配置代理解决 React 项目中的跨域请求问题
使用 package.json 配置代理解决 React 项目中的跨域请求问题 当我们在开发前端应用时,经常会遇到跨域请求的问题。为了解决这个问题,我们可以通过配置代理来实现在开发环境中向后端服务器发送请求。 在 React 项目中,我们可以使用 package…...

生成 Let‘s Encrypt 免费证书
文章目录 1. 安装 acme.sh2. 添加云服务商安全访问密钥并授权管理DNS记录3. 当前 Shell 添加安全访问密钥变量4. 生成证书5. 拷贝证书6. 清理安全访问密钥变量7. 打开脚本自动更新 代码仓库地址:https://github.com/Neilpang/acme.sh 1. 安装 acme.sh yum -y insta…...
)
int128的实现(基本完成)
虽然有一个声明叫_int128但是这并不是C标准: long long 不够用?详解 __int128 - FReQuenter - 博客园 (cnblogs.com) 网络上去找int128的另类实现方法,发现几乎都是在介绍_int128的 然后我就自己想了个办法,当时还没学C…...

【linux】使用 acme.sh 实现了 acme 协议生成免费的SSL 证书
acme.sh 实现了 acme 协议, 可以从 letsencrypt 生成免费的证书. 主要步骤: 安装 acme.sh生成证书copy 证书到 nginx/apache 或者其他服务更新证书更新 acme.sh出错怎么办, 如何调试 下面详细介绍. 1. 安装 acme.sh 安装很简单, 一个命令: curl https://get.acme.sh | sh…...

MACOS上面C/C++获取网卡索引,索引获取网卡接口名
依赖函数: if_nametoindex IF名字 to IF索引 if_indextoname IF索引 to IF名字 MACOS 10.7 版本支援(就是2011年发不OSX的第一个面向用的系统版本) int GetInterfaceIndex(const ppp::string& ifrName) noexcept{if (ifrName.empt…...

解决SSH远程登录开饭板出现密码错误问题
输入“adduser Zhanggong回车”,使用adduser命令创建开发板用户名为Zhanggong 输入密码“123456” 输入密码“123456”...

什么时候用ref和reactive
在Vue 3中,ref和reactive都是用于创建响应式数据的工具,但它们的使用场景有所不同。 使用ref的情况: 基本数据类型:当你需要响应式地处理基本数据类型(如数字、字符串、布尔值)时,应该使用ref…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
