Python 将二维数组或矩阵变为三维
Python 将二维数组或矩阵变为三维
- 引言
- 正文
- 基础
- 拓展
引言
之前,我们已经介绍过了 Python 将一维数组或矩阵变为三维。然而,很多时候,我们也需要对二维矩阵进行操作,这里特来介绍一下如何将二维矩阵扩展为三维。
阅读这一篇前推荐优先阅读 np.concatenate()函数。
正文
基础
import numpy as npsampling_points = 10001arr = np.array([[1, 2],[3, 4]])
arr_3D = arr.reshape(1, 2, 2)
print(arr_3D)
"""
result:
[[[1 2][3 4]]]
"""
采用 reshape 方法我们依然可以做到这一点。
reshape 方法扩展数组或者说矩阵维度几乎是万能的。
拓展
然而做到这一步还不够,如果我们此时有两个一维数组,我们如何将它们组合起来扩展为三维数组呢,这里,我们期望一维数组的元素排列方向朝向 z 轴。我们的想法是先将两个一维数组均扩展为三维的,然后再将它们连接起来。
import numpy as npsampling_points = 10001arr1 = np.array([1, 2])
arr2 = np.array([3, 4])arr1_3D = arr1.reshape(-1, 1, 1)
arr2_3D = arr2.reshape(-1, 1, 1)result = np.concatenate((arr1_3D, arr2_3D), axis=2)print(result)
"""
result:
[[[1 3]][[2 4]]]
"""
可以看到,至此,我们得到了我们想要的结果。
如果大家觉得有用,就请点个赞吧~
相关文章:

Python 将二维数组或矩阵变为三维
Python 将二维数组或矩阵变为三维 引言正文基础 拓展 引言 之前,我们已经介绍过了 Python 将一维数组或矩阵变为三维。然而,很多时候,我们也需要对二维矩阵进行操作,这里特来介绍一下如何将二维矩阵扩展为三维。 阅读这一篇前推…...

区块链与Solidity详细介绍及基本语法使用
一、区块链简介 区块链是一种分布式数据库技术,它以块的形式存储数据,并通过加密算法确保数据的安全性。每个块包含一系列交易,并通过哈希值与前一个块相连接,形成一个链式结构。这种结构使得数据难以被篡改,因为任何对…...

题目 1253: 老王赛马
题目描述: 赛马是一古老的游戏,早在公元前四世纪的中国,处在诸侯割据的状态,历史上称为“战国时期”。在魏国作官的孙膑,因为受到同僚庞涓的迫害,被齐国使臣救出后,到达齐国国都。 赛马是当时最受齐国贵族…...
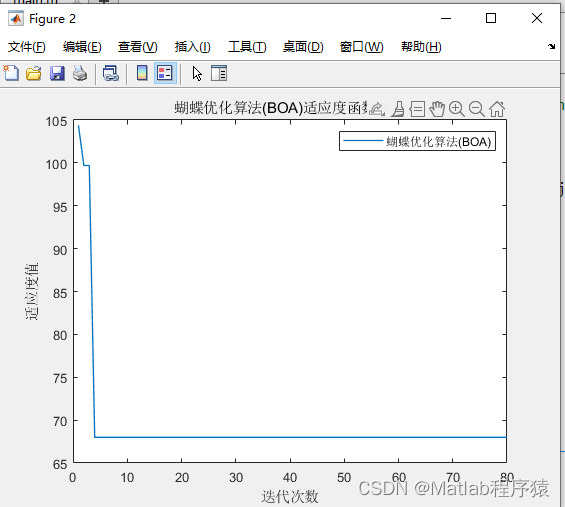
【MATLAB源码-第144期】基于matlab的蝴蝶优化算法(BOA)无人机三维路径规划,输出做短路径图和适应度曲线。
操作环境: MATLAB 2022a 1、算法描述 蝴蝶优化算法(Butterfly Optimization Algorithm, BOA)是基于蝴蝶觅食行为的一种新颖的群体智能算法。它通过模拟蝴蝶个体在寻找食物过程中的嗅觉导向行为以及随机飞行行为,来探索解空间…...
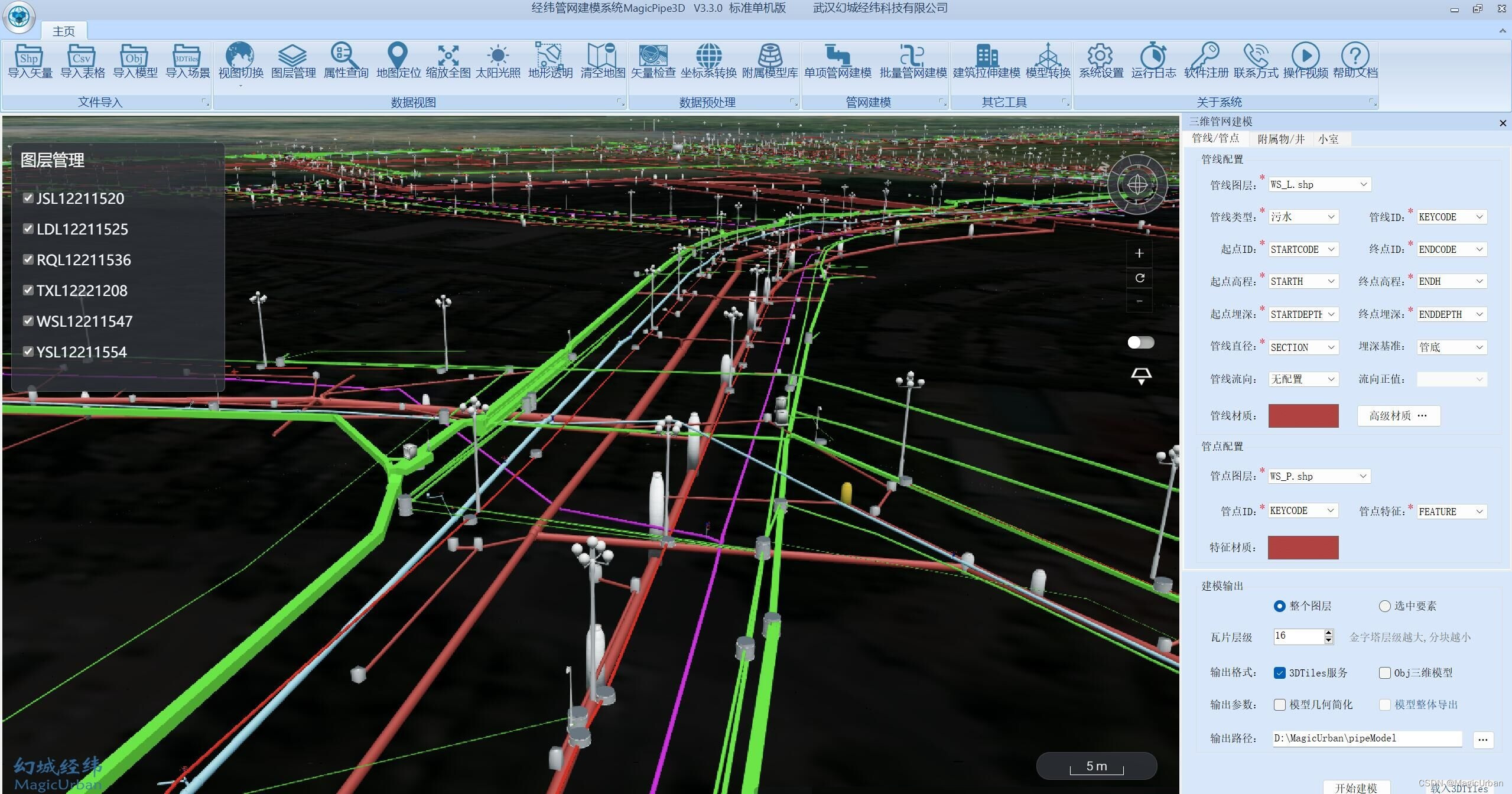
地下管线管网三维建模工具MagicPipe3D V3.4.2发布
经纬管网建模系统MagicPipe3D,本地离线参数化构建地下管网三维模型(包括管道、接头、附属设施等),输出标准3DTiles服务、Obj模型等格式,支持Cesium、Unreal、Unity、Osg等引擎加载进行三维可视化、语义查询、专题分析&…...
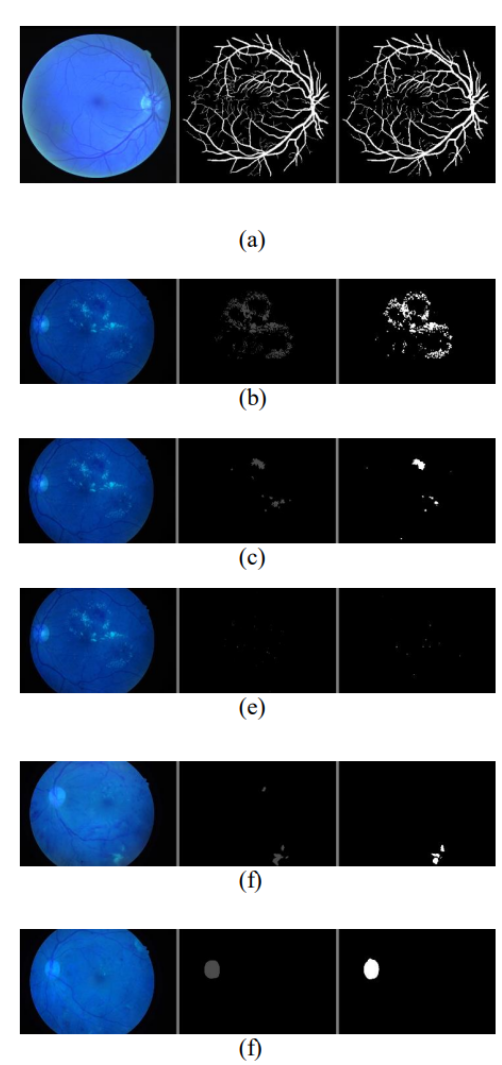
糖尿病性视网膜病变(DR)的自动化检测和分期
糖尿病性视网膜病变(DR)的自动化检测和分期 提出背景DR的阶段及其特征 历年解法计算机视觉方法多分类方法 新的解法深度学习方法迁移学习大模型多模型集成全流程分析 总结特征1:图像分割特征2:疾病分级特征3:治疗建议生…...
C 标准库 - <errno.h>
在C语言编程中,<errno.h> 头文件扮演着至关重要的角色,它提供了一个全局变量 errno 以及一系列预定义宏,用于指示系统调用或库函数执行过程中发生的错误。这些宏有助于程序员诊断和处理运行时错误。 errno 变量 extern int errno;err…...
基于springboot+vue的房屋租赁管理系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…...
Sora----打破虚实之间的最后一根枷锁----这扇门的背后是人类文明的晟阳还是最后的余晖
目录 一.Sora出道即巅峰 二.为何说Sora是该领域的巨头 三.Sora无敌的背后究竟有怎样先进的处理技术 1.Spacetime Latent Patches 潜变量时空碎片,建构视觉语言系统 2.扩散模型与Diffusion Transformer,组合成强大的信息提取器 3.DiT应用于潜变量时…...

C语言之static关键字详解
C语言之static关键字详解_c语言static-CSDN博客 1.变量 2.局部变量和全局变量 3.变量的作用域 4.变量的生命周期 二、static关键字的作用 三、static关键字修饰局部变量 四、static关键字修饰全局变量 五、static关键字修饰函数...
Redis高性能原理
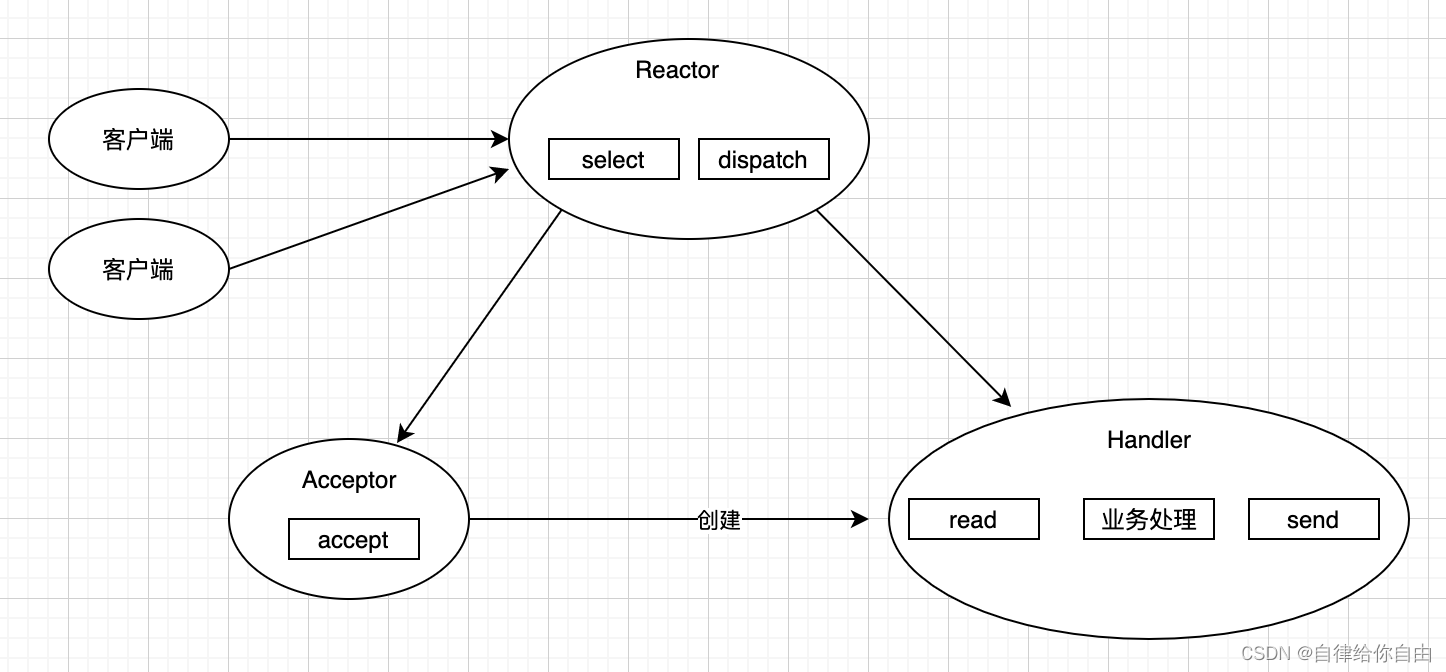
redis大家都知道拥有很高的性能,每秒可以支持上万个请求,这里探讨下它高性能的原理。单线程架构和io多路复用技术。 一,单线程架构 单线程架构指的是命令执行核心线程是单线程的,数据持久化、同步、异步删除是其他线程在跑的。re…...
MSS与cwnd的关系,rwnd又是什么?
慢启动算法是指数递增的 这种指数增长的方式是慢启动算法的一个核心特点,它确保了TCP连接在开始传输数据时能够快速地探测网络的带宽容量,而又不至于过于激进导致网络拥塞。具体来说: 初始阶段:当TCP连接刚建立时,拥…...
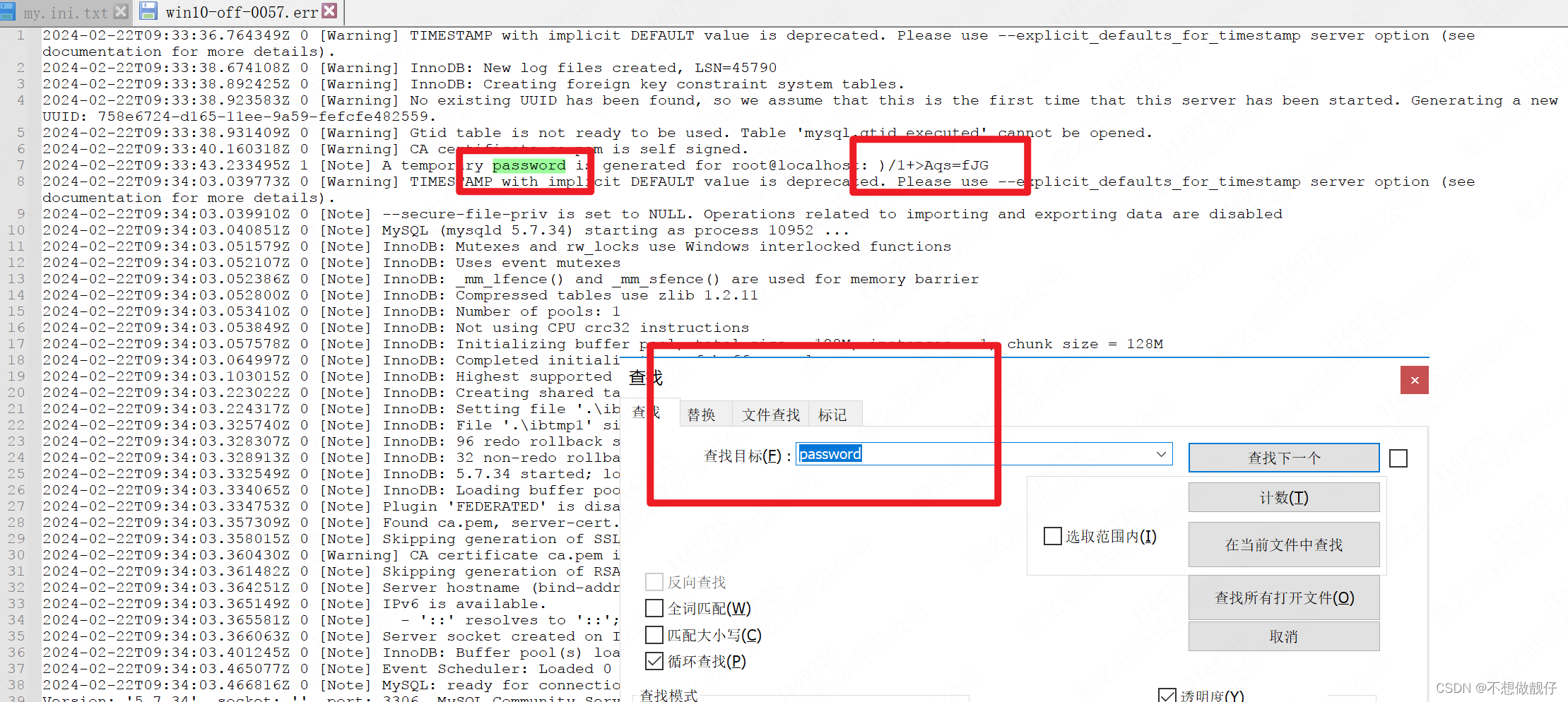
解决两个MySQL5.7报错
目录 1.启动不了MySQL,报错缺少MSVCR120.dll去官网下载vcredist_x64.exe运行安装进入管理员CMD 2.本地计算机 上的 mysql 服务启动后停止。某些服务在未由其他服务或程序使用时将自动停止,Fatal error: Can‘t open and lock privilege tables: Table ‘…...

[OpenAI]继ChatGPT后发布的Sora模型原理与体验通道
前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家:https://www.captainbed.cn/z ChatGPT体验地址 文章目录 前言OpenAI体验通道Spacetime Latent Patches 潜变量时空碎片, 建构视觉语言系统…...

机器人初识 —— 电机传动系统
一、背景 波士顿动力公司开发的机器人,其电机传动系统是其高性能和动态运动能力的核心部分。电机传动系统通常包括以下几个关键组件: 1. **电动马达**:波士顿动力的机器人采用了先进的电动马达作为主要的动力源,如伺服电机或步进…...
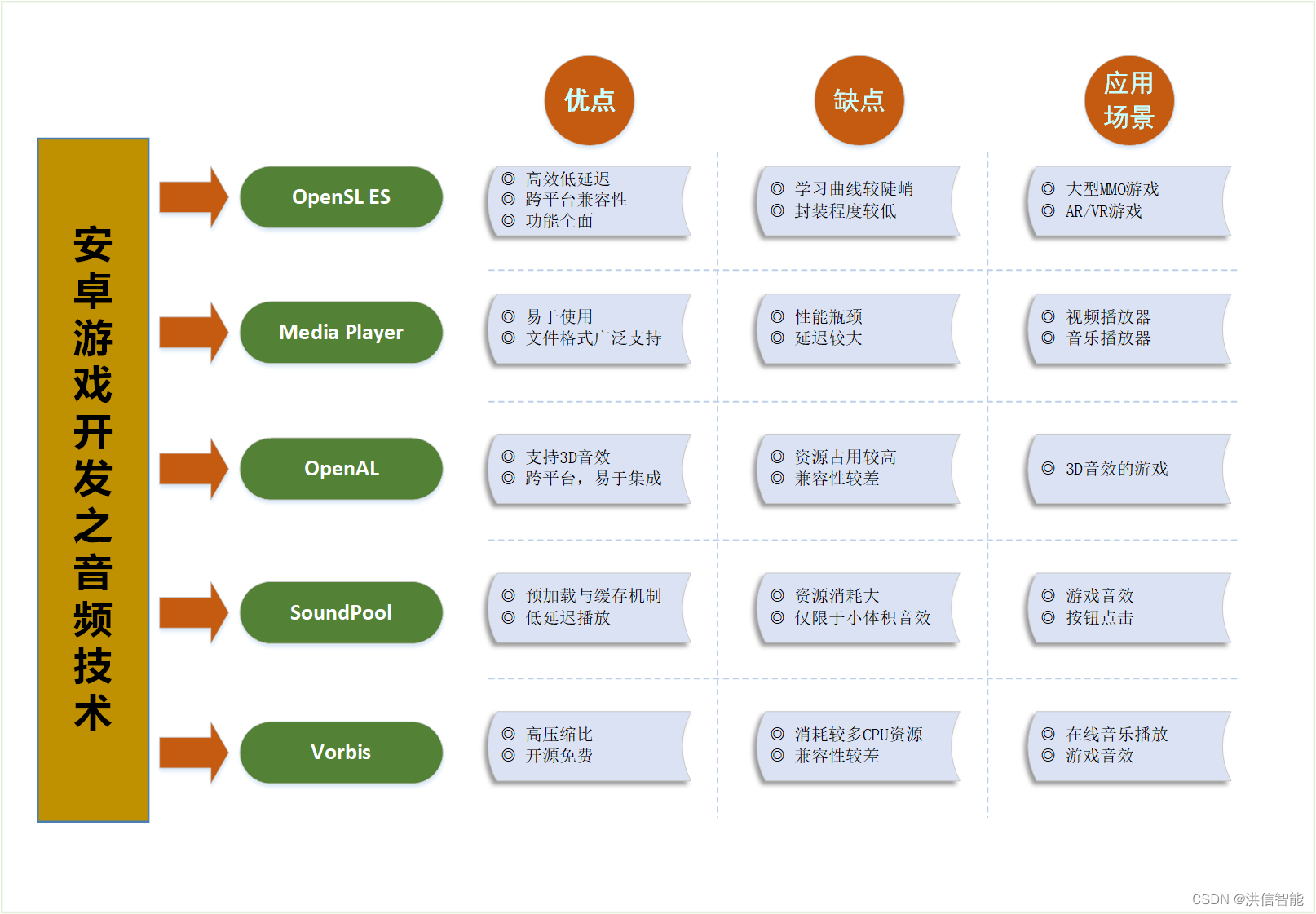
安卓游戏开发之音频技术优劣分析
一、引言 在安卓游戏开发中,音频处理技术扮演着至关重要的角色,它不仅能够增强游戏的沉浸感和玩家体验,还能通过声音效果传达关键的游戏信息。以下将对几种常见的安卓游戏音频处理技术进行优劣分析,并结合应用场景来阐述其特点。 …...

在C语言中,设置Linux系统时间
C 语言中使用 mktime 函数和 stime 函数来处理时间。 处理之前,需要先获取当前的时间戳。并使用当前的时间戳生成struct tm,struct tm是C语言中用于表示日期和时间的结构体,通常用于在程序中操作和处理日期时间信息。它包含了以下成员变量&a…...

golang k8s包管理工具
k8s包管理工具Helm Helm简介Helm基础概念Helm安装Helm命令Helm Chart(图表)Chart语法Chart变量替换Chart模板控制结构Chart模板函数Chart迭代和范围Helm Values(值)Helm Release(发布)Helm Repository&…...
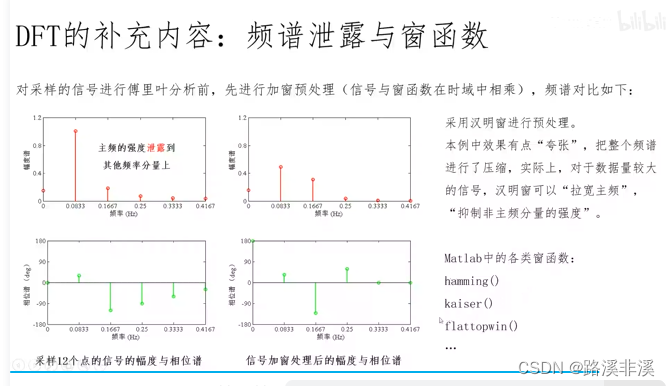
数字信号处理:傅里叶分析
本文主要参考视频如下: 数字信号处理9-1_线性时不变系统对复指数信号的响应_哔哩哔哩_bilibili 傅里叶分析的主要研究内容如下所示: 注意,计算机中使用的离散傅里叶变换并不是离散时间傅里叶变换; 前四种都是理论上的变换方式&…...

pat 甲级 1051 Pop Sequence
思想:如果要弹出一个数,那么说明比它小的数字已经进栈了,所以要在一个数num输入之后把比它小的数都输入到栈中,直到栈满或者valnum时结束入栈操作。如果valnum,将这个值弹出,否则说明整个序列存在问题,把fl…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
