Leetcode2583. 二叉树中的第 K 大层和
Every day a Leetcode
题目来源:2583. 二叉树中的第 K 大层和
解法1:层序遍历 + 排序
先使用层序遍历计算出树的每一层的节点值的和,保存在数组 levelSum 中。然后将数组进行排序,返回第 k 大的值。需要考虑数组长度小于 k 的边界情况。
代码:
/** @lc app=leetcode.cn id=2583 lang=cpp** [2583] 二叉树中的第 K 大层和*/// @lc code=start
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:long long kthLargestLevelSum(TreeNode *root, int k){if (root == nullptr)return -1;vector<long long> levelSum;queue<TreeNode *> q;q.push(root);while (!q.empty()){int size = q.size();long long sum = 0LL;for (int i = 0; i < size; i++){TreeNode *node = q.front();q.pop();sum += node->val;if (node->left)q.push(node->left);if (node->right)q.push(node->right);}levelSum.push_back(sum);}if (levelSum.size() < k)return -1;sort(levelSum.begin(), levelSum.end());return levelSum[levelSum.size() - k];}
};
// @lc code=end
结果:
复杂度分析:
时间复杂度:O(nlogn),其中 n 是二叉树的节点个数。
空间复杂度:O(n),其中 n 是二叉树的节点个数。
解法2:层序遍历 + 快速选择
也可以使用快速选择的算法快速定位第 k 大的元素。
代码:
// 层序遍历 + 快速选择class Solution
{
public:long long kthLargestLevelSum(TreeNode *root, int k){if (root == nullptr)return -1;vector<long long> levelSum;queue<TreeNode *> q;q.push(root);while (!q.empty()){int size = q.size();long long sum = 0LL;for (int i = 0; i < size; i++){TreeNode *node = q.front();q.pop();sum += node->val;if (node->left)q.push(node->left);if (node->right)q.push(node->right);}levelSum.push_back(sum);}int n = levelSum.size();if (k > n)return -1;ranges::nth_element(levelSum, levelSum.begin() + (n - k));return levelSum[n - k];}
};
结果:
复杂度分析:
时间复杂度:O(nlogn),其中 n 是二叉树的节点个数。
空间复杂度:O(n),其中 n 是二叉树的节点个数。
相关文章:

Leetcode2583. 二叉树中的第 K 大层和
Every day a Leetcode 题目来源:2583. 二叉树中的第 K 大层和 解法1:层序遍历 排序 先使用层序遍历计算出树的每一层的节点值的和,保存在数组 levelSum 中。然后将数组进行排序,返回第 k 大的值。需要考虑数组长度小于 k 的边…...
(六)激光线扫描-三维重建
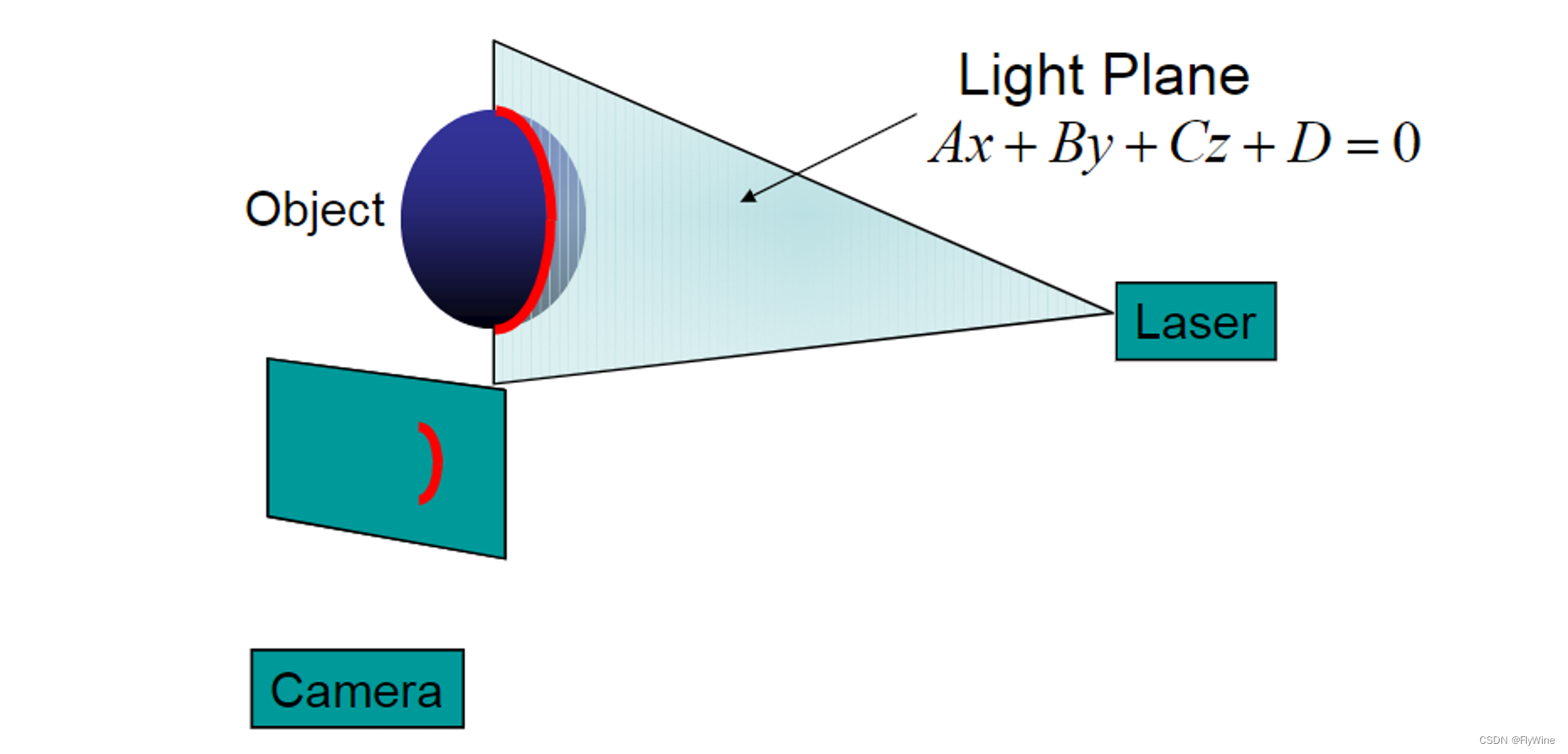
本篇文章是《激光线扫描-三维重建》系列的最后一篇。 1. 基础理论 1.1 光平面 在之前光平面标定的文章中,已经提到过了,是指 激光发射器投射出一条线,形成的一个扇形区域平面就是光平面。 三维空间中平面的公式是: A X + B Y + C Z + D = 0 A X+B Y+C Z+D=0...
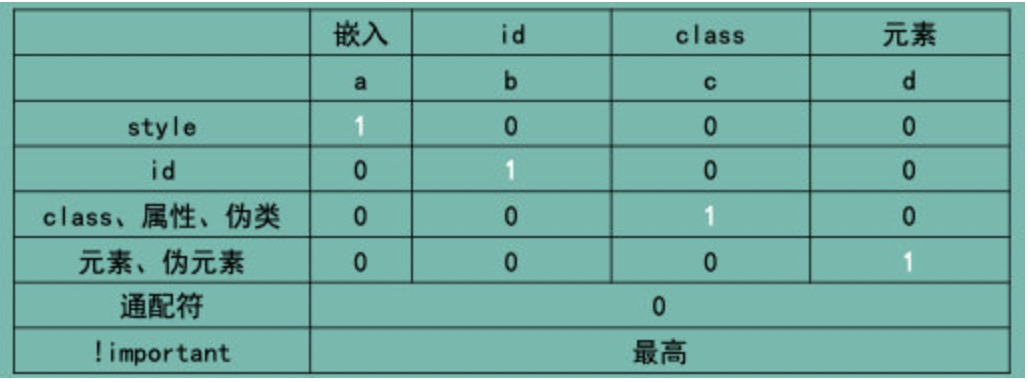
CSS 面试题汇总
CSS 面试题汇总 1. 介绍下 BFC 及其应 参考答案: 参考答案: 所谓 BFC,指的是一个独立的布局环境,BFC 内部的元素布局与外部互不影响。 触发 BFC 的方式有很多,常见的有: 设置浮动overflow 设置为 auto、scr…...
定制你的【Spring Boot Starter】,加速开发效率
摘要: 本文将介绍如何创建一个自定义的 Spring Boot Starter,让您可以封装常用功能和配置,并在多个 Spring Boot 项目中共享和重用。 1. 简介 Spring Boot Starter 是 Spring Boot 框架中的一种特殊的依赖项,它用于快速启动和配置…...
)
Vue源码系列讲解——生命周期篇【二】(new Vue)
目录 1. 前言 2. new Vue()都干了什么 3 . 合并属性 4. callHook函数如何触发钩子函数 5. 总结 1. 前言 上篇文章中介绍了Vue实例的生命周期大致分为4个阶段,那么首先我们先从第一个阶段——初始化阶段开始入手分析。从生命周期流程图中我们可以看到ÿ…...

JavaScript 设计模式之观察者模式
观察者模式 观察者模式又被称为发布-订阅模式,使用一个对象来收集订阅者,在发布时遍历所有订阅者,然后将信息传递给订阅者,可以这样来实现一个简单的模式 const Observable (function () {let __messages {}return {register:…...

数据结构D4作业
1.实现单向循环链表的功能 loop.c #include "loop.h" loop_p create_loop() { loop_p H(loop_p)malloc(sizeof(loop)); if(HNULL) { printf("创建失败\n"); return NULL; } H->len0; H->nextH; ret…...
springboot750人职匹配推荐系统
springboot750人职匹配推荐系统 获取源码——》公主号:计算机专业毕设大全...
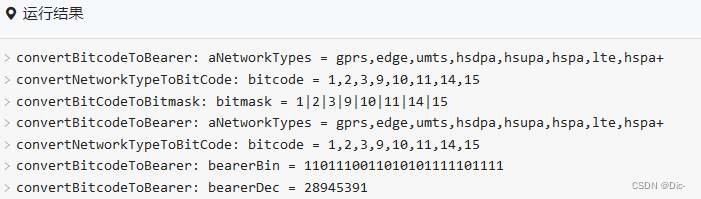
【笔记】【开发方案】APN 配置参数 bitmask 数据转换(Android KaiOS)
一、参数说明 (一)APN配置结构对比 平台AndroidKaiOS文件类型xmljson结构每个<apn>标签是一条APN,包含完成的信息层级数组结构,使用JSON格式的数据。最外层是mcc,其次mnc,最后APN用数组形式配置&am…...
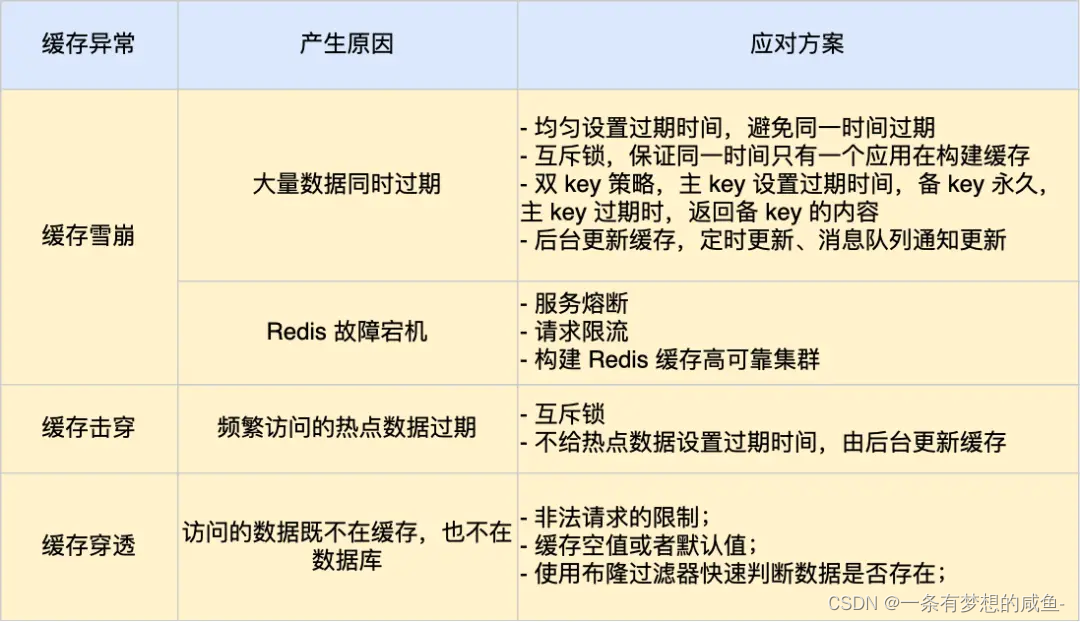
Redis篇之缓存雪崩、击穿、穿透详解
学习材料:https://xiaolincoding.com/redis/cluster/cache_problem.html 缓存雪崩 什么是缓存雪崩 在面对业务量较大的查询场景时,会把数据库中的数据缓存至redis中,避免大量的读写请求同时访问mysql客户端导致系统崩溃。这种情况下&#x…...

【深度学习笔记】3_2线性回归的从零实现
注:本文为《动手学深度学习》开源内容,仅为个人学习记录,无抄袭搬运意图 3.2 线性回归的从零开始实现 在了解了线性回归的背景知识之后,现在我们可以动手实现它了。尽管强大的深度学习框架可以减少大量重复性工作,但若…...

Apache Maven简介
Maven 简介 Apache Maven 是一个用于项目构建、依赖管理和项目信息管理的强大工具。它基于项目对象模型(Project Object Model,POM)进行构建,通过描述项目的结构和依赖关系来管理项目的构建过程。 以下是 Apache Maven 的一些关键原理和工作流程: 项目对象模型(POM)…...
#12解决request中getReader()和getInputStream()只能调用一次的问题
目录 1、背景 2、解决方案 2.1、自定义HttpServletRequestWrapper 2.2、JsonRequestHeaderParamsHelper 2.3、HttpServletRequestReplacedFilter 2.4、使用 1、背景 当前系统Content-Type为application/json,参数接收方式采用RequestBody和RequestParam&#…...

直接插入排序+希尔排序+冒泡排序+快速排序+选择排序+堆排序+归并排序+基于统计的排序
插入排序:直接插入排序、希尔排序 交换排序:冒泡排序、快速排序 选择排序:简单选择排序、堆排序 其他:归并排序、基于统计的排序 一、直接插入排序 #include<stdio.h> #include<stdlib.h> /* 直接插入排序&#…...
)
Java高级 / 架构师 场景方案 面试题(二)
1.双十一亿级用户日活统计如何用 Redis快速计算 在双十一这种亿级用户日活统计的场景中,使用Redis进行快速计算的关键在于利用Redis的数据结构和原子操作来高效地统计和计算数据。以下是一个基于Redis的日活统计方案: 选择合适的数据结构: …...
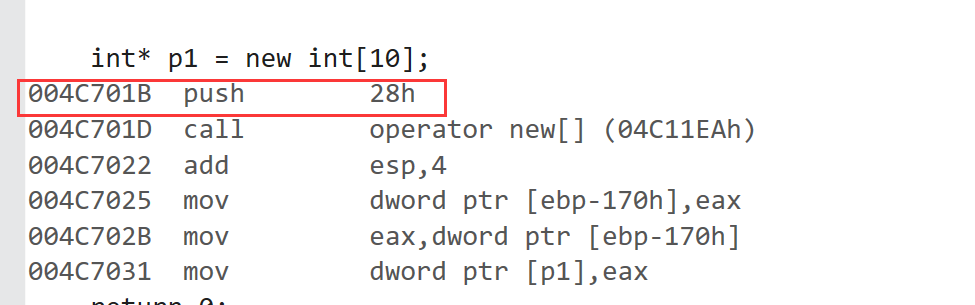
C/C++内存管理学习【new】
文章目录 一、C/C内存分布二、C语言中动态内存管理方式:malloc/calloc/realloc/free三、C内存管理方式3.1 new/delete操作内置类型3.2 new和delete操作自定义类型四、operator new与operator delete函数五、new和delete的实现原理5.1 内置类型 六、定位new表达式(pl…...

选择适合你的编程语言
引言 在当今瞬息万变的技术领域中,选择一门合适的编程语言对于个人职业发展和技术成长至关重要。每种语言都拥有独特的设计哲学、应用场景和市场需求,因此,在决定投入时间和精力去学习哪种编程语言时,我们需要综合分析多个因素&a…...

【力扣每日一题】力扣106从中序和后序遍历序列构造二叉树
题目来源 力扣106从中序和后序遍历序列构造二叉树 题目概述 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 思路分析 后序遍历序列的最末尾数…...

logback日志回滚原理
日志输出主要依赖RollingFileAppender、TimeBasedRollingPolicy、SizeAndTimeBasedFNATP。 RollingFileAppender 主要用于生成日志文件,格式化内容再输出到日志文件TimeBasedRollingPolicy 设置回滚策略,如果发现日志输出的时间超过单位时间,…...

[C#]winform基于opencvsharp结合pairlie算法实现低光图像增强黑暗图片变亮变清晰
【低光图像增强介绍】 在图像处理领域,低光图像增强是一个具有挑战性的任务。由于光线不足,这些图像往往呈现出低对比度、高噪声和细节丢失等问题,严重影响了图像的视觉效果和后续分析的准确性。因此,开发有效的低光图像增强方法…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
