jax可微分编程的笔记(2)
jax可微分编程的笔记(2)
第2章 自动微分
自动微分和符号求导有诸多的相似之处:它们同样依赖于计算图
的构建,同样依赖于求导的递归实现。从某种意义上来说,它们
甚至有完全相同的数据结构。不过,二者的区别也是显著的:
符号微分侧重于符号,而自动微分则侧重于数值。
自动微分是一种专门化的计算图网络。各种所谓的“神经网络”,
只不过是某种特殊的计算图结构,而由此引申出所谓的“深度学习”
的概念,不过是可微分编程框架的这一概念外延的子集。
2.1.1 前向模式的理论
自动微分的前向模式适用于函数输入参数个数较少,输出参数个数
较多的场合。
2.1.2 前向模式的二元数诠释
从数学的角度来看,我们可以将自动微分的前向模式理解为将函数
延拓到二元数域的结果。
从本质上来说,二元数幂零元E^2=0,承接了同调论中的重要结论
d。df=0 ,在这样的视角下,二元数与微分操作在数学结构上的相似
就成为了显然。
2.2 反向模式
直观上来看,反向模式的算法与前向模式相比显得极为不同,然而,
自动微分的反向模式与前向模式,其实具有相当的一致性。
2.2.1 反向模式的理论
对结点的处理将会沿着计算图构建顺序的相反方向执行,这样的求导
实现方式,称为自动微分的反向模式,由此引出的算法又称为反向
传播算法。
第一次反向传播,我们可以计算出雅可比矩阵的一行,因此,自动微分
的反向模式适用于函数的输入变量较多,而输出维数较少的场合。
在反向模式的代码现实中,要对计算图网络进行拓扑排序,用于拓扑排序
的卡恩算法是卡恩在1962年提出的.它允许我们尝试对任意的有向图
进行拓扑排序
2.2.2 反向模式与前向模式的统一
在前向模式时,如果将计算图所定义的函数f扩展到二元数域,其切值
中将包含着雅可比矩阵作用于x的结果。
当一个函数的输入x发生了变化时,函数的输出f将如何变化?在前向
模式中,在保留到一阶的情形下,x的微小变化 delta x 将会导致输出
的f产生变化 delta f.这样的响应关系将会随着正向的计算,穿过一
整张由函数f所定义的计算图,这样的数学行为被我们用二元数的运算
法则进行了严格的描述。
下面我们希望询问上述问题的反问题:当一个函数的输出f发生了变化
时,函数的输入x将如何变化?在一个机械臂的控制问题中,自动微分
的前向模式相当于根据每个机械节点的形态及转 速,控制机械臂末端
的状态;而自动微分的反向模式,则是通过机械臂终端节点的空间状态
及运动趋势,控制其每个关节的运动参数。
对于一个函数数值的计算,只有在它所有的输入的值全部完成计算后
才能进行计算,这样的计算顺序其实就是一种拓扑序。
相关文章:
)
jax可微分编程的笔记(2)
jax可微分编程的笔记(2) 第2章 自动微分 自动微分和符号求导有诸多的相似之处:它们同样依赖于计算图 的构建,同样依赖于求导的递归实现。从某种意义上来说,它们 甚至有完全相同的数据结构。不过,二者的区…...
在Linux服务器上部署一个单机项目
目录 一、jdk安装 二、tomcat安装 三、MySQL安装 四、部署项目 一、jdk安装 1. 上传jdk安装包 jdk-8u151-linux-x64.tar.gz 进入opt目录,将安装包拖进去 2. 解压安装包 这里需要解压到usr/local目录下,在这里我新建一个文件夹保存解压后的文件 [r…...
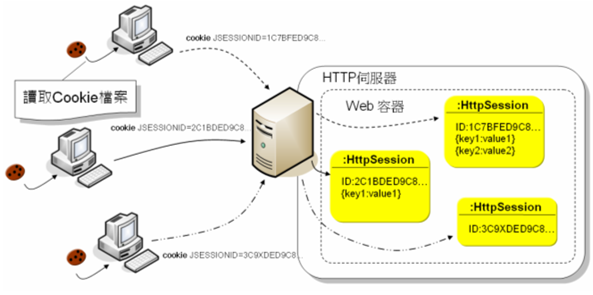
HTTP概要
文章目录 什么是HTTP?URL的结构请求报文结构请求方法GETHEADPOSTPUTDELETETRACEOPTIONSCONNECTPATCH解释 请求头字段 响应报文结构响应状态响应头字段 HTTP会话3次握手无状态协议 什么是HTTP? HTTP,即Hypertext Transfer Protocol(超文本传输协议) 它是一个”请…...
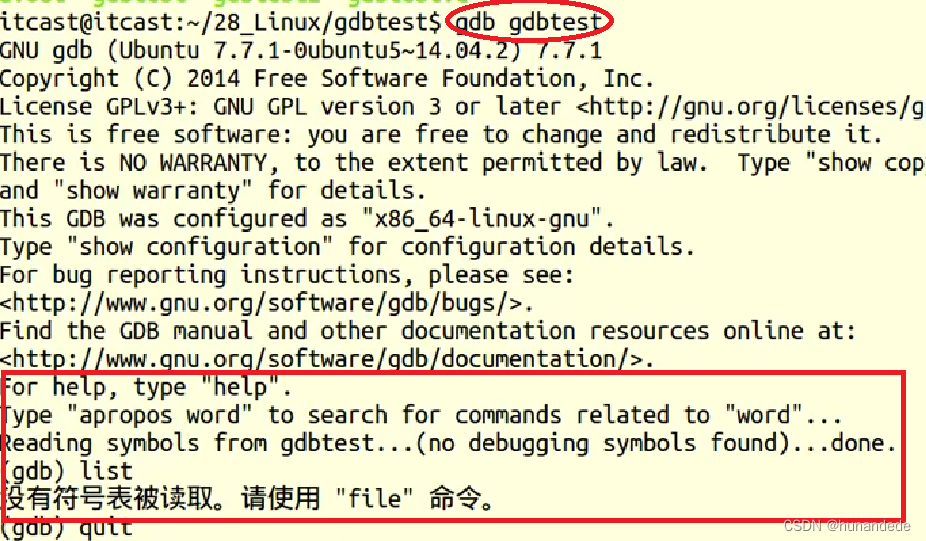
128 Linux 系统编程6 ,C++程序在linux 上的调试,GDB调试
今天来整理 GDB 调试。 在windows 上我们使用vs2017开发,可以手动的加断点,debug。 那么在linux上怎么加断点,debug呢?这就是今天要整理的GDB调试工具了。 那么有些同学可能会想到:我们在windows上开发,…...
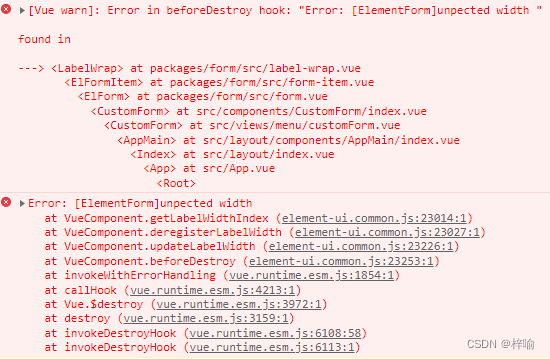
vue2的ElementUI的form表单报错“Error: [ElementForm]unpected width”修复
1. 问题 ElementUI的form表单,当动态切换显示表单时报错 Error: [ElementForm]unpected width。 翻译过来就是form表单的label宽度width出了问题。 2. 分析 参数说明类型可选值默认值label-width表单域标签的宽度,例如 ‘50px’。作为 Form 直接子元…...

Linux 网络命令指南
目录 配置IP地址和子网掩码 网络接口的详细信息 测试与目标主机的连通性 下载文件或内容 远程登录,进行远程管理和协作 CentOS / Red Hat(使用 firewalld) 关闭防火墙 开启防火墙 配置TCP端口(假设使用3306端口ÿ…...

vue3组件间的通信,通过props,emit,provide和inject把数据传递N个层级,expose和ref实现父组件调用子组件方法
文章目录 一、父组件数据传递N个层级的子组件vue3 provide 与 injectA组件名称 app.vueB组件名称 provideB.vueC组件名称 provideCSetup.vue 二、使用v-model指令实现父子组件的双向绑定父组件名称 app.vue子组件名称 v-modelSetup.vue 三、父组件props向子组件传值子组件 prop…...
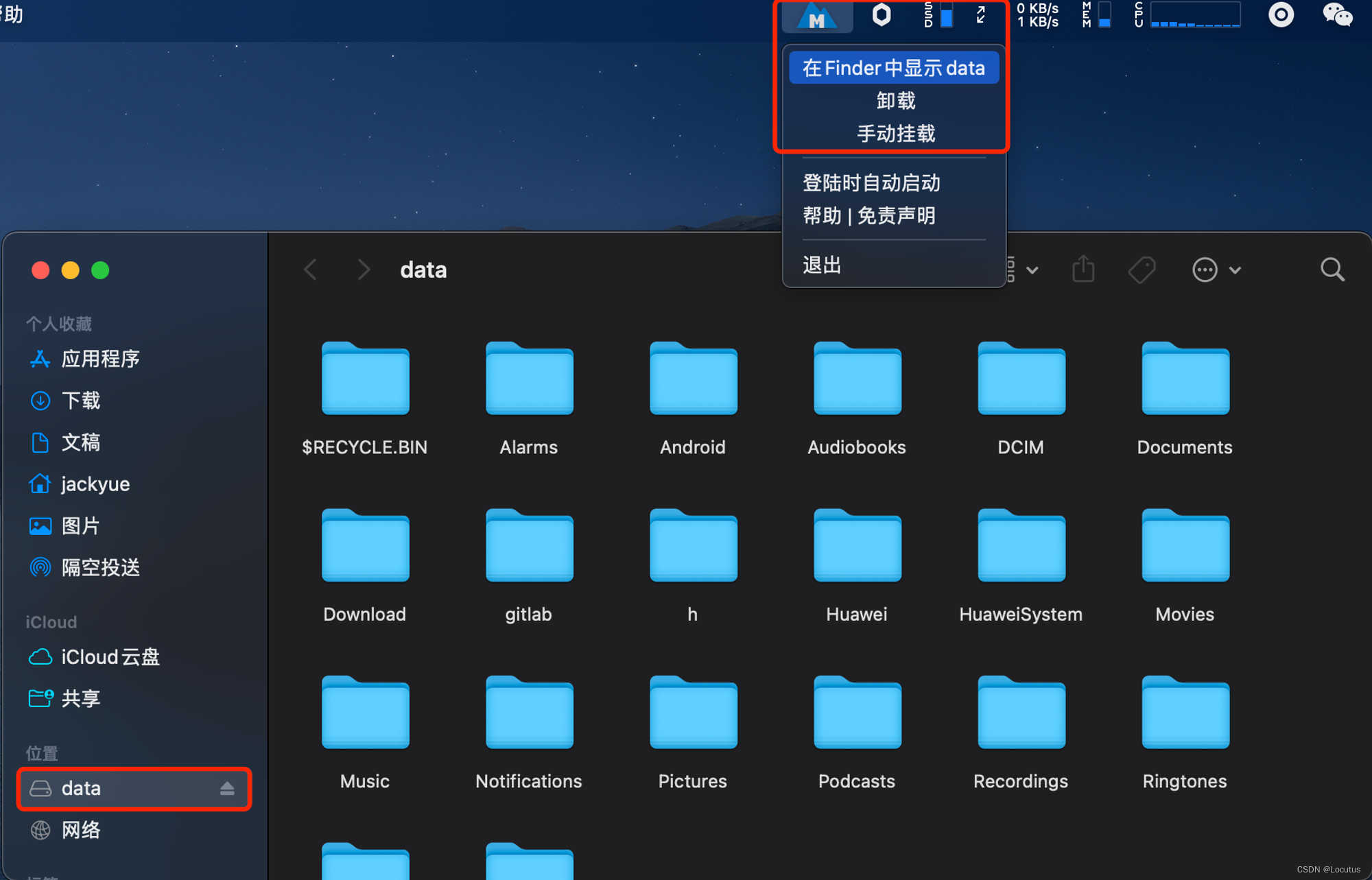
开源免费的NTFS for mac工具mounty
开源免费的NTFS for mac工具mounty 安装依赖 brew install gromgit/fuse/ntfs-3g-macbrew install --cask macfuse安装mounty 如果已经安装macFUSE和ntfs-3g-mac,可以直接点击下载的dmg安装包,安装升级。第一次启动mounty,你需要接受一系列…...

Sora-OpenAI 的 Text-to-Video 模型:制作逼真的 60s 视频片段
OpenAI 推出的人工智能功能曾经只存在于科幻小说中。 2022年,Openai 发布了 ChatGPT,展示了先进的语言模型如何实现自然对话。 随后,DALL-E 问世,它利用文字提示生成令人惊叹的合成图像。 现在,他们又推出了 Text-t…...
4 buuctf解题
[CISCN 2019 初赛]Love Math1 打开题目 题目源码 <?php error_reporting(0); //听说你很喜欢数学,不知道你是否爱它胜过爱flag if(!isset($_GET[c])){show_source(__FILE__); }else{//例子 c20-1$content $_GET[c];if (strlen($content) > 80) {die("…...
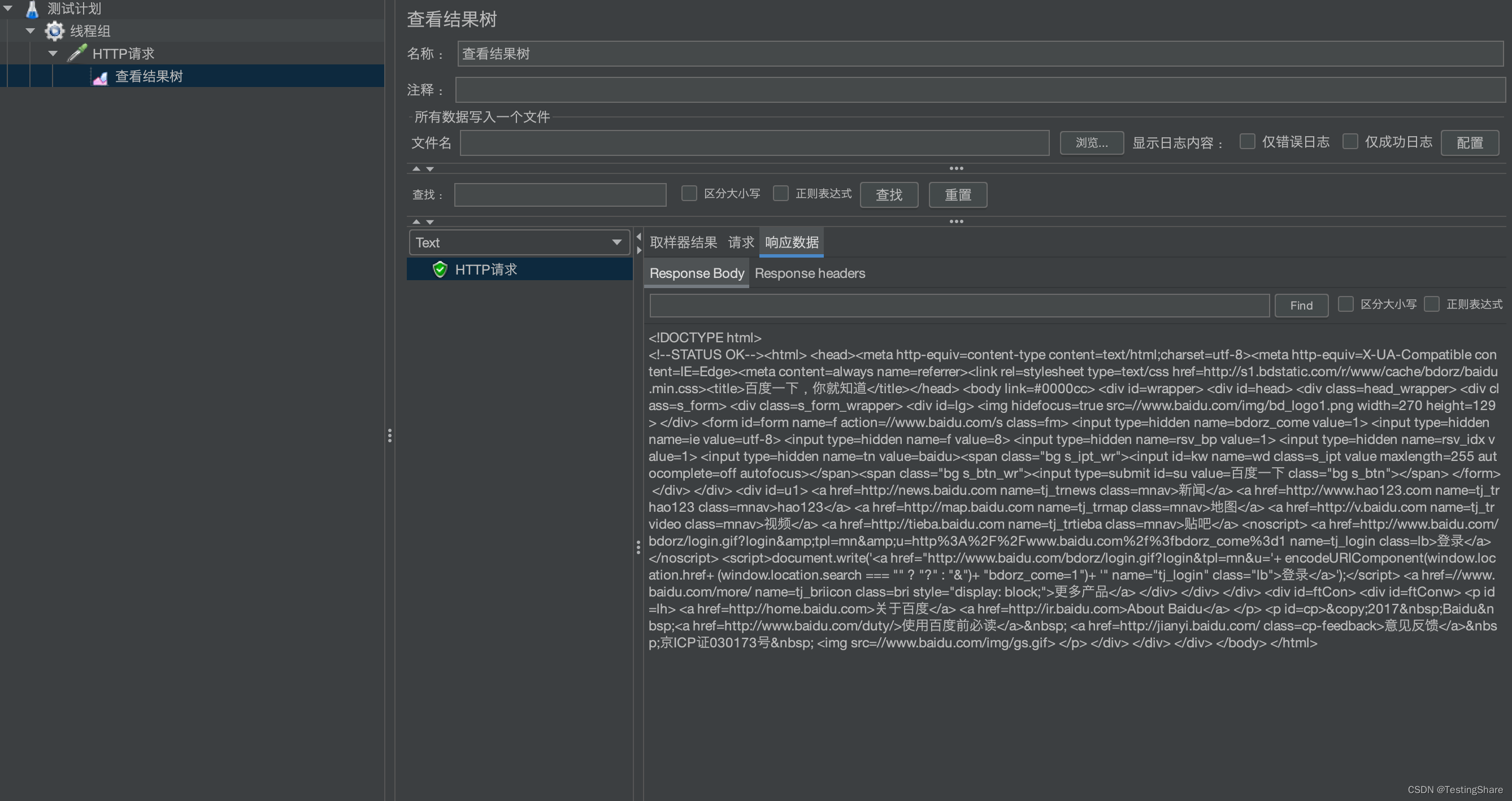
Jmeter基础(3) 发起一次请求
目录 Jmeter 一次请求添加线程组添加HTTP请求添加监听器 Jmeter 一次请求 用Jmeter进行一次请求的过程,需要几个步骤呢? 1、添加线程组2、添加HTTP请求3、添加监听器,查看结果树 现在就打开jmeter看下如何创建一个请求吧 添加线程组 用来…...
视频怎么变成gif动图?一招教你在线转换
MP4是一种常见的视频文件格式,它可以包含音频和视频数据,并支持高质量的视频压缩。MP4视频可以呈现连续的动态效果,可以包含平滑的运动、音频等多媒体元素。而GIF动图是由一系列静态图像组成的,通过快速连续播放这些帧来创造出动态…...
Leetcode2583. 二叉树中的第 K 大层和
Every day a Leetcode 题目来源:2583. 二叉树中的第 K 大层和 解法1:层序遍历 排序 先使用层序遍历计算出树的每一层的节点值的和,保存在数组 levelSum 中。然后将数组进行排序,返回第 k 大的值。需要考虑数组长度小于 k 的边…...
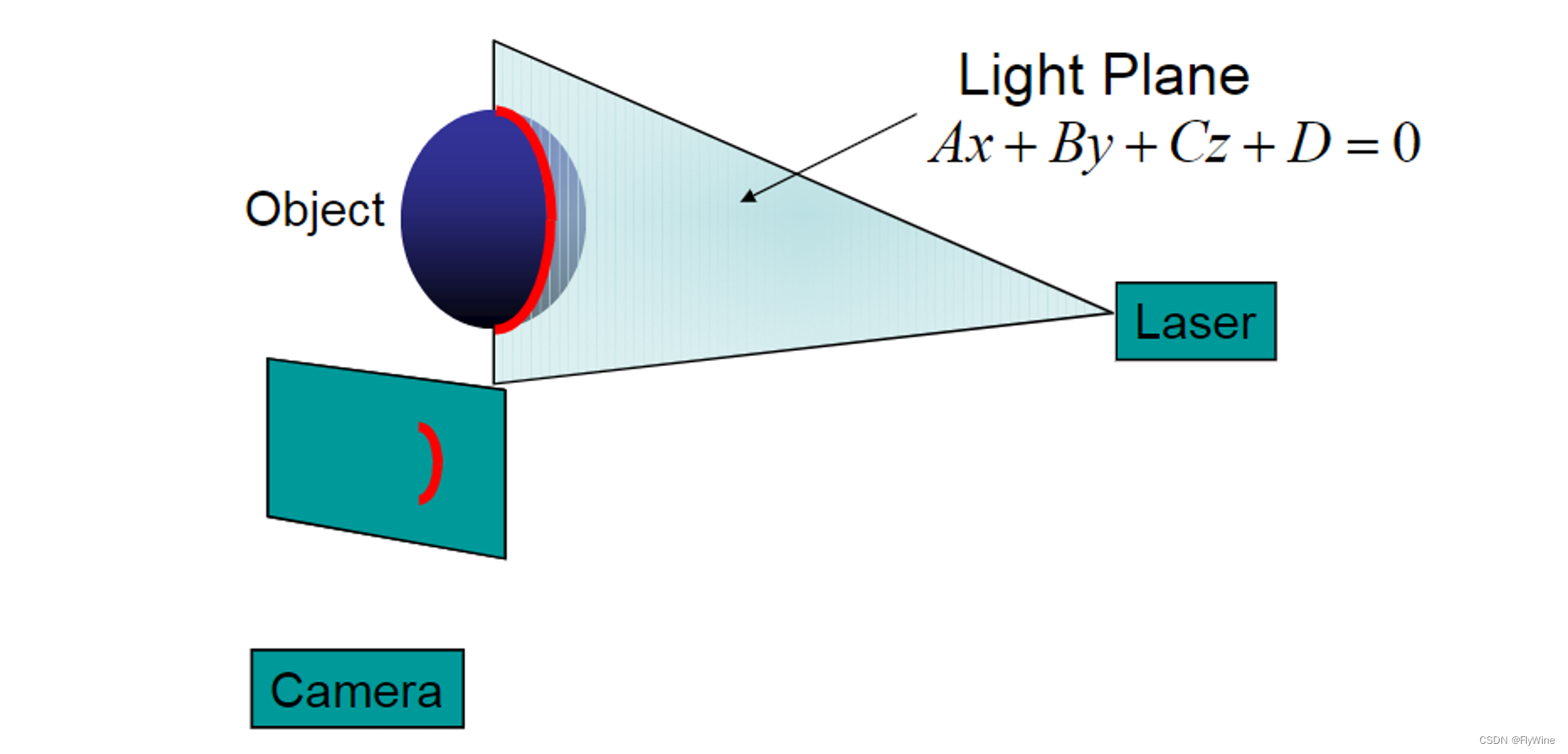
(六)激光线扫描-三维重建
本篇文章是《激光线扫描-三维重建》系列的最后一篇。 1. 基础理论 1.1 光平面 在之前光平面标定的文章中,已经提到过了,是指 激光发射器投射出一条线,形成的一个扇形区域平面就是光平面。 三维空间中平面的公式是: A X + B Y + C Z + D = 0 A X+B Y+C Z+D=0...
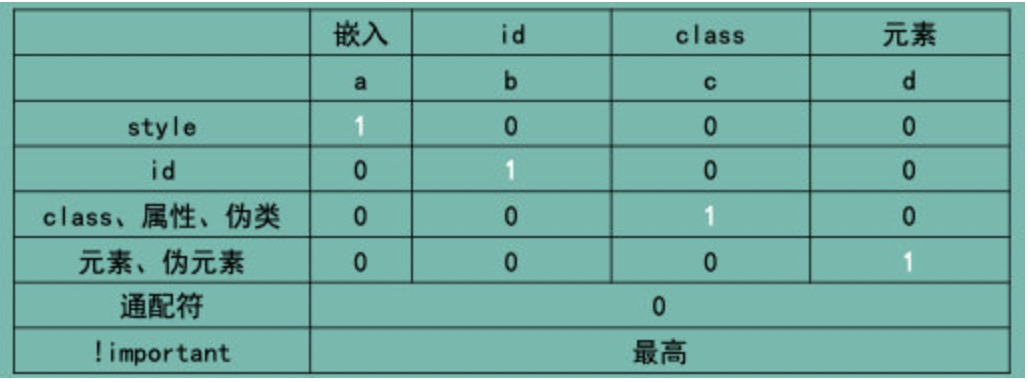
CSS 面试题汇总
CSS 面试题汇总 1. 介绍下 BFC 及其应 参考答案: 参考答案: 所谓 BFC,指的是一个独立的布局环境,BFC 内部的元素布局与外部互不影响。 触发 BFC 的方式有很多,常见的有: 设置浮动overflow 设置为 auto、scr…...
定制你的【Spring Boot Starter】,加速开发效率
摘要: 本文将介绍如何创建一个自定义的 Spring Boot Starter,让您可以封装常用功能和配置,并在多个 Spring Boot 项目中共享和重用。 1. 简介 Spring Boot Starter 是 Spring Boot 框架中的一种特殊的依赖项,它用于快速启动和配置…...
)
Vue源码系列讲解——生命周期篇【二】(new Vue)
目录 1. 前言 2. new Vue()都干了什么 3 . 合并属性 4. callHook函数如何触发钩子函数 5. 总结 1. 前言 上篇文章中介绍了Vue实例的生命周期大致分为4个阶段,那么首先我们先从第一个阶段——初始化阶段开始入手分析。从生命周期流程图中我们可以看到ÿ…...

JavaScript 设计模式之观察者模式
观察者模式 观察者模式又被称为发布-订阅模式,使用一个对象来收集订阅者,在发布时遍历所有订阅者,然后将信息传递给订阅者,可以这样来实现一个简单的模式 const Observable (function () {let __messages {}return {register:…...

数据结构D4作业
1.实现单向循环链表的功能 loop.c #include "loop.h" loop_p create_loop() { loop_p H(loop_p)malloc(sizeof(loop)); if(HNULL) { printf("创建失败\n"); return NULL; } H->len0; H->nextH; ret…...
springboot750人职匹配推荐系统
springboot750人职匹配推荐系统 获取源码——》公主号:计算机专业毕设大全...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
