普中51单片机学习(AD转换)
AD转换
分辨率
ADC的分辨率是指使输出数字量变化一个相邻数码所需输入模拟电压的变化量。常用二进制的位数表示。例如12位ADC的分辨率就是12位,或者说分辨率为满刻度的1/(2^12)。
一个10V满刻度的12位ADC能分辨输入电压变化最小值是10V×1/(2^12 )=2.4mV。
量化误差
ADC把模拟量变为数字量,用数字量近似表示模拟量,这个过程称为量化。量化误差是ADC的有限位数对模拟量进行量化而引起的误差。实际上,要准确表示模拟量,ADC的位数需很大甚至无穷大。一个分辨率有限的ADC的阶梯状转换特性曲线与具有无限分辨率的ADC转换特性曲线(直线)之间的最大偏差即是量化误差。
偏移误差
偏移误差是指输入信号为零时,输出信号不为零的值,所以有时又称为零值误差。假定ADC没有非线性误差,则其转换特性曲线各阶梯中点的连线必定是直线,这条直线与横轴相交点所对应的输入电压值就是偏移误差。
满刻度误差
满刻度误差又称为增益误差。ADC的满刻度误差是指满刻度输出数码所对应的实际输入电压与理想输入电压之差。
线性度
线性度有时又称为非线性度,它是指转换器实际的转换特性与理想直线的最大偏差。
绝对精度
在一个转换器中,任何数码所对应的实际模拟量输入与理论模拟输入之差的最大值,称为绝对精度。对于ADC而言,可以在每一个阶梯的水平中点进行测量,它包括了所有的误差。
转换速率
ADC的转换速率是能够重复进行数据转换的速度,即每秒转换的次数。而完成一次A/D转换所需的时间(包括稳定时间),则是转换速率的倒数。

逐次逼近式ADC的转换原理
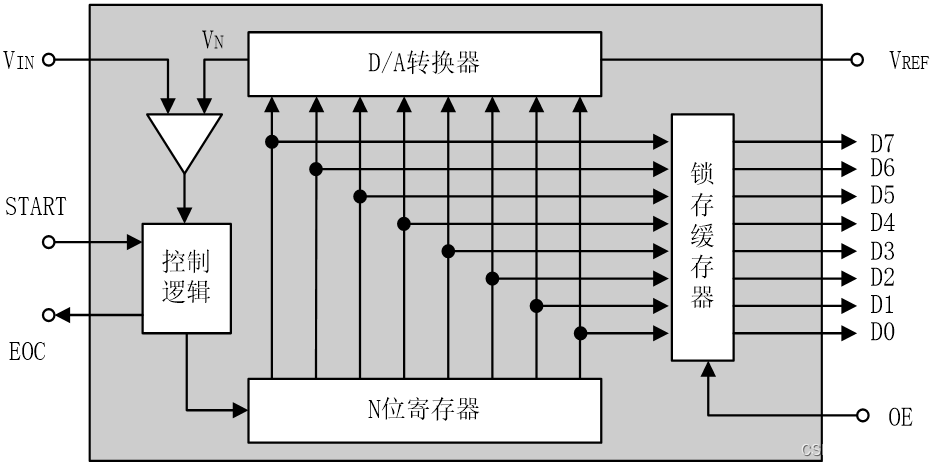
逐次逼近式AD转换器与计数式A/D转换类似,只是数字量由“逐次逼近寄存器SAR”产生。SAR使用“对分搜索法”产生数字量,以8位数字量为例,SAR首先产生8位数字量的一半,即10000000B,试探模拟量Vi的大小,若Vn>Vi,清除最高位,若Vn<Vi,保留最高位。在最高位确定后,SAR又以对分搜索法确定次高位,即以低7位的一半y1000000B(y为已确定位) 试探模拟量Vi的大小。在bit6确定后,SAR以对分搜索法确定bit5位,即以低6位的一半yy100000B(y为已确定位) 试探模拟量的大小。重复这一过程,直到最低位bit0被确定,转换结束。
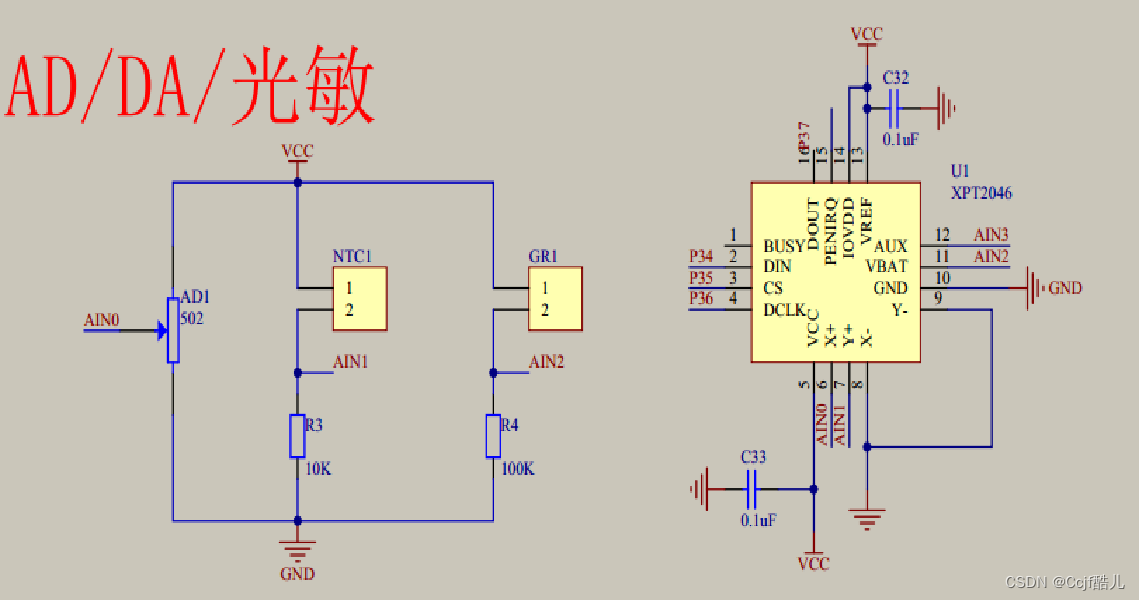
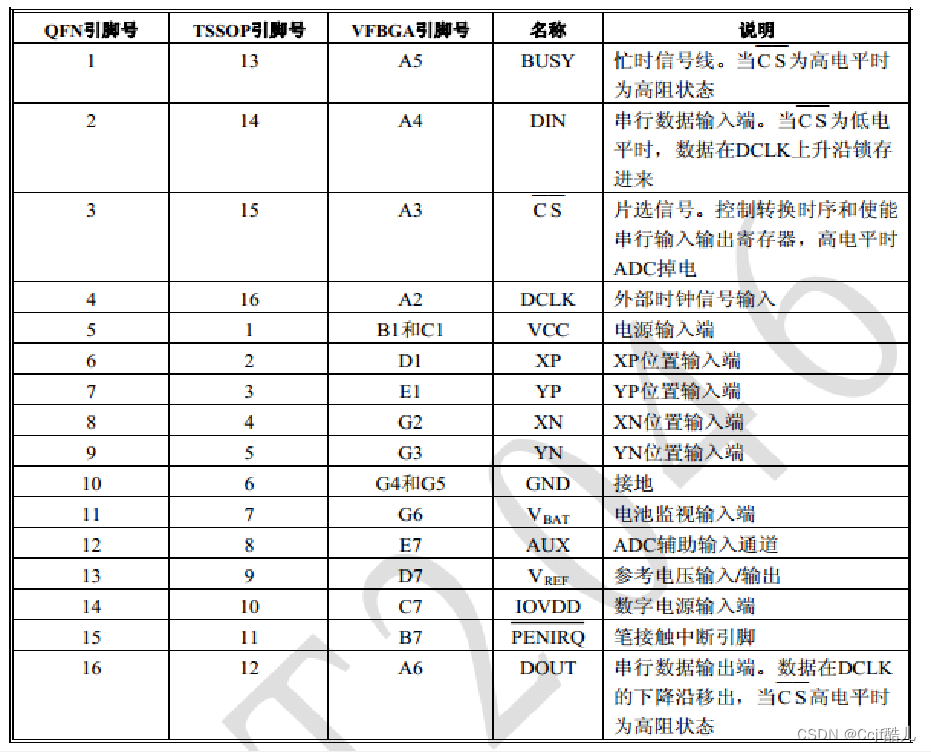
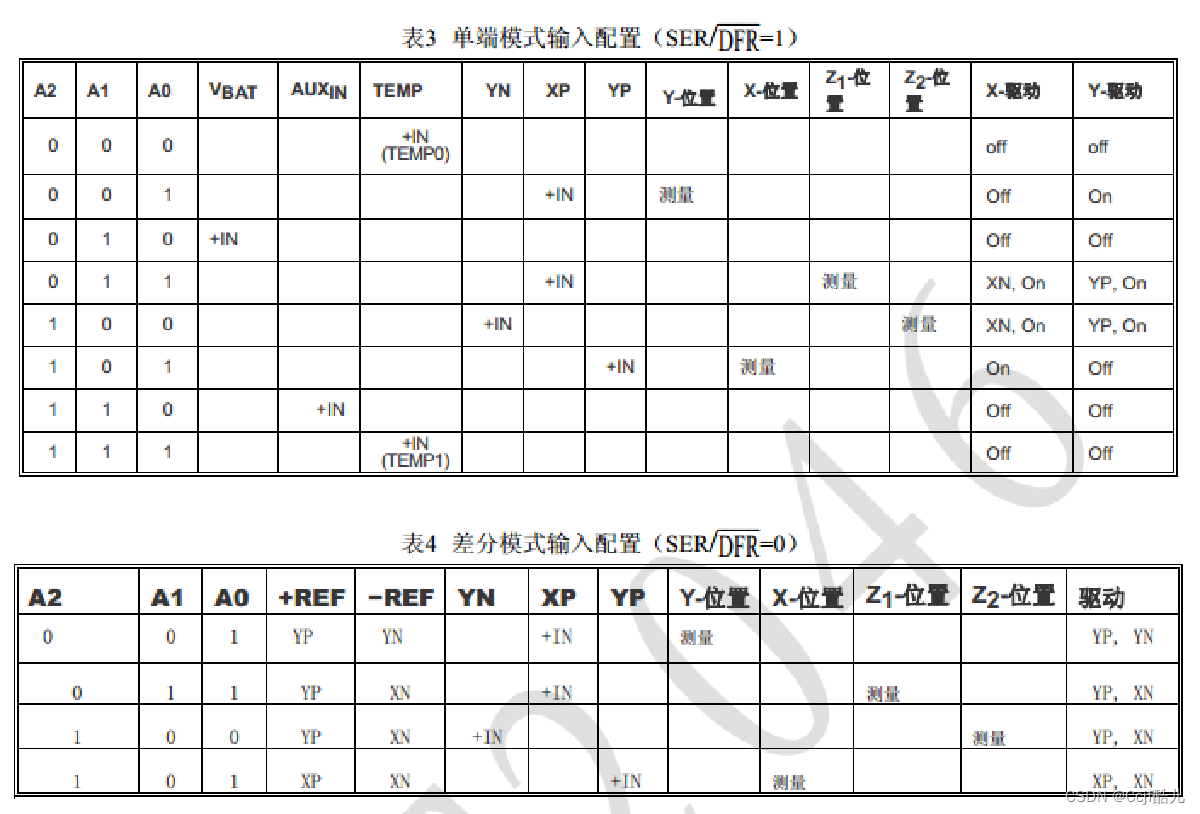
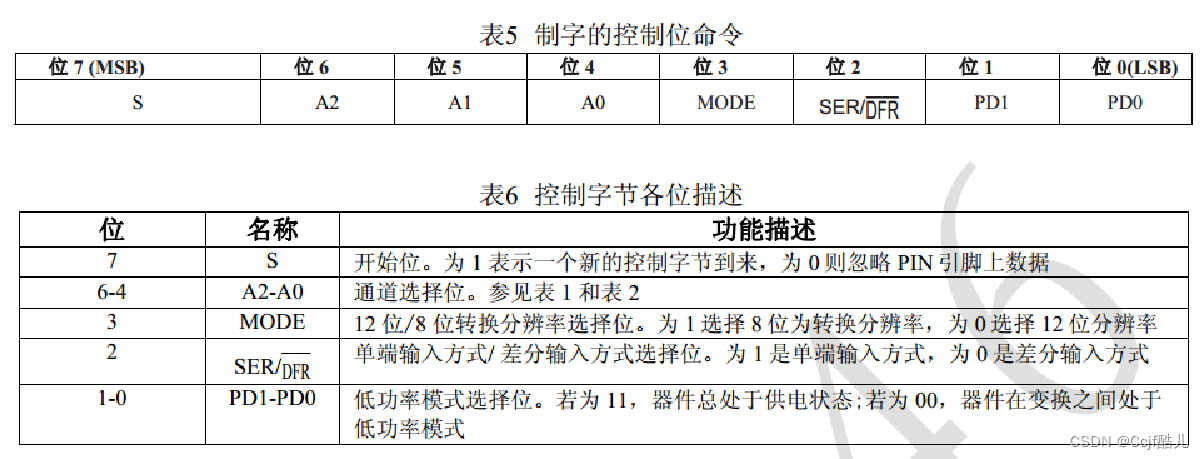
- 如果要检测转换电位器模拟信号,控制字命令寄存器值为0X94或者0XB4.
- 如果要检测转换热敏电阻模拟信号,控制字命令寄存器值为0XD4.
- 如果要检测转换光敏电阻模拟信号,控制字命令寄存器值为0XA4.
- 如果要检测转换AIN3通道上模拟信号,控制字命令寄存器值为0XE4.
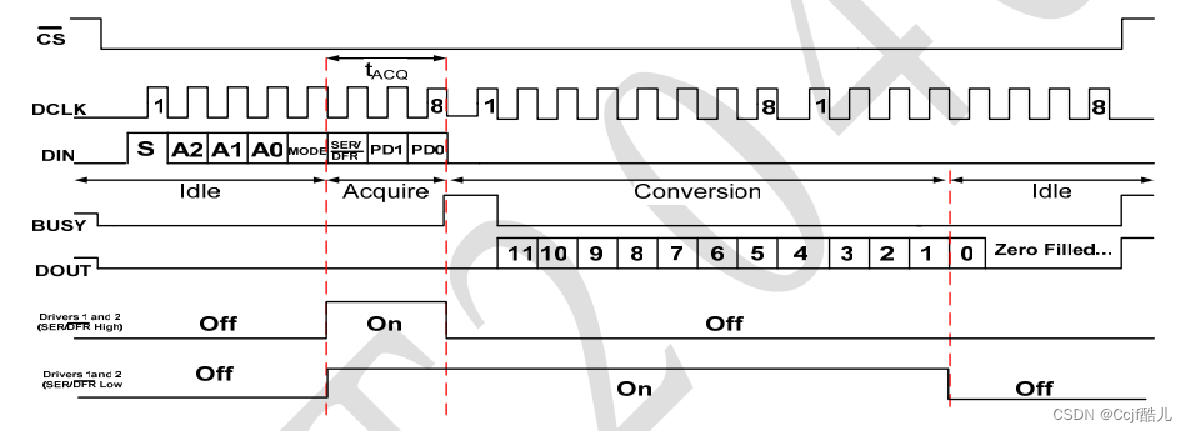
实验代码
XPT2046.h
#ifndef _XPT2046_H
#define _XPT2046_H#include "reg52.h"
#include "intrins.h"#ifndef uchar
#define uchar unsigned char
#endif#ifndef uint
#define uint unsigned int
#endifsbit DOUT=P3^7;
sbit CLK=P3^6;
sbit DIN=P3^4;
sbit CS=P3^5;uint Read_AD_Data(uchar cmd);
uint SPI_Read(void);
void SPI_Write(uchar dat);#endif
XPT2046.c
#include "XPT2046.h"void SPI_Write(uchar dat)
{uchar i;CLK=0;for(i=0;i<8;i++){DIN=dat>>7;dat<<=1;CLK=0;CLK=1;}
}uint SPI_Read(void)
{uint i,dat=0;CLK=0;for(i=0;i<12;i++){dat<<=1;CLK=1;CLK=0;dat|=DOUT;}return dat;
}uint Read_AD_Data(uchar cmd)
{uchar i;uint AD_Value;CLK=0;CS=0;SPI_Write(cmd);for(i=0;i<6;i++){ }CLK=1;_nop_();_nop_();CLK=0;_nop_();_nop_();AD_Value=SPI_Read();CS=1;return AD_Value;
}
main.c
#include "reg52.h"
#include "XPT2046.h"typedef unsigned int u16;
typedef unsigned char u8;sbit LSA=P2^2;
sbit LSB=P2^3;
sbit LSC=P2^4;u8 disp[4];
u8 code smgduan[10]={0x3f,0x06,0x5b,0x4f,0x66,0x6d,0x7d,0x07,0x7f,0x6f};void delay(u16 i)
{while(i--);
}void datapros()
{u16 temp;static u8 i;if(i==50){i=0;temp=Read_AD_Data(0x94);}i++;disp[0]=smgduan[temp/1000];disp[1]=smgduan[temp%1000/100];disp[2]=smgduan[temp%100/10];disp[3]=smgduan[temp%10];
}void DigDisplay()
{u8 i;for(i=0;i<4;i++){switch(i) //位选,选择点亮的数码管,{case(0):LSA=0;LSB=0;LSC=0; break;//显示第0位case(1):LSA=1;LSB=0;LSC=0; break;//显示第1位case(2):LSA=0;LSB=1;LSC=0; break;//显示第2位case(3):LSA=1;LSB=1;LSC=0; break;//显示第3位 }P0=disp[3-i];//发送数据delay(100); //间隔一段时间扫描 P0=0x00;//消隐}
}void main()
{while(1){datapros();DigDisplay();}
}
相关文章:

普中51单片机学习(AD转换)
AD转换 分辨率 ADC的分辨率是指使输出数字量变化一个相邻数码所需输入模拟电压的变化量。常用二进制的位数表示。例如12位ADC的分辨率就是12位,或者说分辨率为满刻度的1/(2^12)。 一个10V满刻度的12位ADC能分辨输入电压变化最小值是10V1/(2^12 )2.4mV。 量化误差 …...

YoloV8改进策略:主干网络改进|MogaNet——高效的多阶门控聚合网络
文章目录 摘要1、简介2、相关工作2.1、视觉Transformers2.2、ViT时代的卷积网络3、从多阶博弈论交互的角度看表示瓶颈4、方法论4.1、MogaNet概述4.2、多阶门控聚合4.3、通过通道聚合进行多阶特征重新分配4.4、实现细节5、实验5.1、ImageNet分类5.2、密集预测任务5.3、消融实验和…...

Sora:OpenAI引领创新浪潮的AI视频模型
Sora:OpenAI引领创新浪潮的AI视频模型 OpenAI作为人工智能领域的佼佼者,接下来,让我们一起深入了解Sora的技术特点、应用场景以及它对未来创作方式的潜在影响。 首先,让我们来探讨Sora的技术特点。Sora是一种基于深度学习的视频生…...

torch报错:[winerror 126] 找不到指定的模块torch_python.dll“ or one of its dependencies.
[winerror 126] 找不到指定的模块。 error loading "d:\miniconda\envs\action_env\lib\site-packages\torch\lib\torch_python.dll" or one of its dependencies. 在使用这个yolov5模块的时候发现了这个错误,错误原因是因为python版本和torch版本冲突。…...
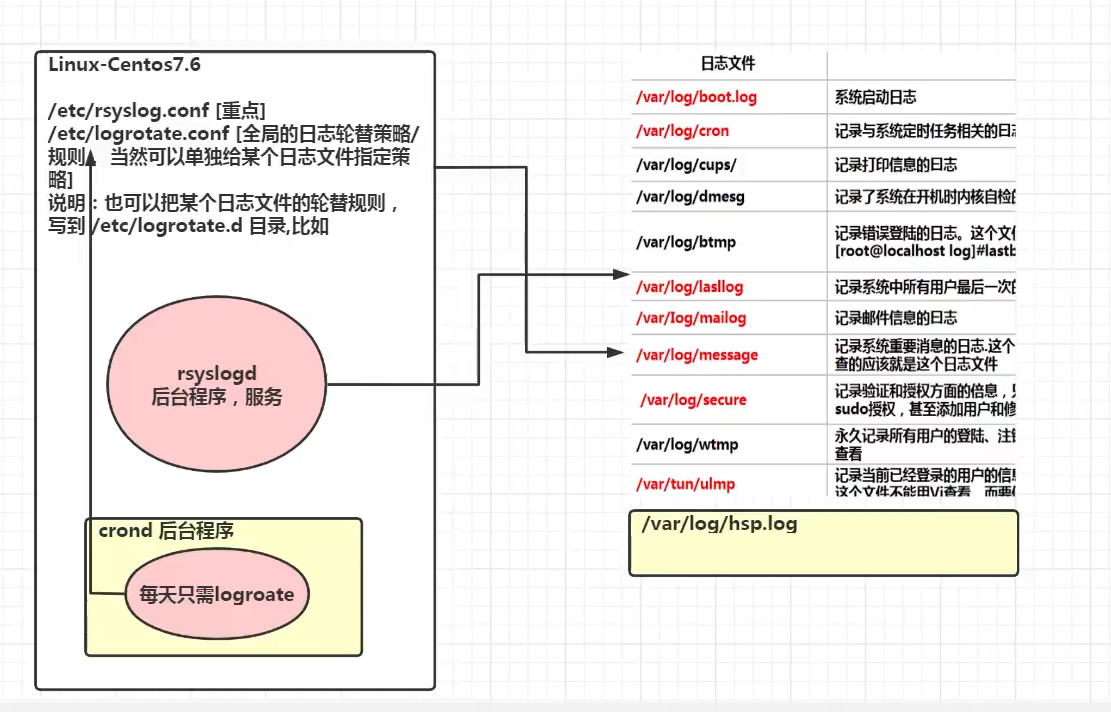
Linux日志轮替
文章目录 1. 基本介绍2. 日志轮替文件命名3. logrotate 配置文件4. 把自己的日志加入日志轮替5. 日志轮替机制原理6. 查看内存日志 1. 基本介绍 日志轮替就是把旧的日志文件移动并改名,同时建立新的空日志文件,当旧日志文件超出保存的范围之后ÿ…...

Docker Container(容器)
"在哪里走散,你都会找到我~" Docker 容器 什么是容器? 通俗来讲,容器是镜像运行的实体。我们对于镜像的认知是,“存储在磁盘上的只读文件”。当我们启动一个容器的本质,就是启动一个进程,即容器…...

week04day03(爬虫 beautifulsoup4、)
一. 使用bs4解析网页 下载bs4 - pip install beautifulsoup4 使用的时候 import bs4专门用于解析网页的第三方库 在使用bs4的时候往往会依赖另一个库lxml pip install lxml 网页代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><…...
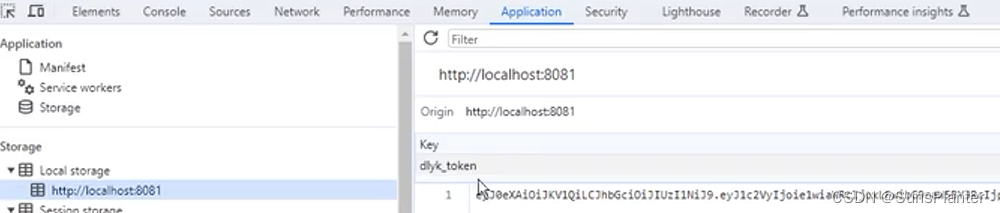
04 动力云客之登录后获取用户信息+JWT存进Redis+Filter验证Token + token续期
1. 登录后获取用户信息 非常好实现. 只要新建一个controller, 并调用SS提供的Authentication对象即可 package com.sunsplanter.controller;RestController public class UserController {GetMapping(value "api/login/info")public R loginInfo(Authentication a…...

RISC-V知识总结 —— 指令集
资源1: RISC-V China – RISC-V International 资源2: RISC-V International – RISC-V: The Open Standard RISC Instruction Set Architecture 资源3: RV32I, RV64I Instructions — riscv-isa-pages documentation 1. 指令集架构的类型 在讨论RISC-V或任何处理器架构时&…...
基于Java jsp+mysql+Spring的汽车出租平台租赁网站平台设计和实现
基于Java jspmysqlSpring的汽车出租平台租赁网站平台设计和实现 博主介绍:5年java开发经验,专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐留…...
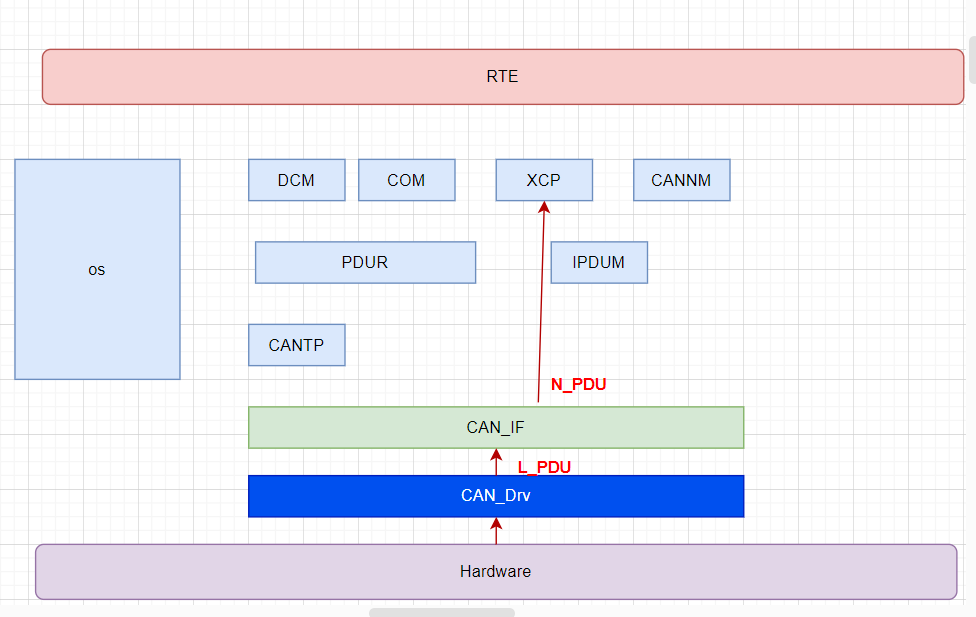
[AutoSar]BSW_Com 01 Can通信入门
目录 关键词平台说明一、车身CAN简介二、相关模块三、Can报文分类及信号流路径3.1 应用报文3.2 应用报文(多路复用multiplexer)3.3 诊断报文3.4 网络管理报文3.5 XCP报文(标定报文) 关键词 嵌入式、C语言、autosar、OS、BSW 平台…...

离散数学 第七单元 tree
目录 树的定义 树的特点 Spanning Tree 生成树(重要!) 生成树算法 DFS 深度优先 BFS 广度优先 Minimun Spanning Tree 最小生成树 Kruscal算法 Prim算法 根树 根数的遍历 前序遍历 中序遍历 后序遍历 表达式的二叉树 中缀…...
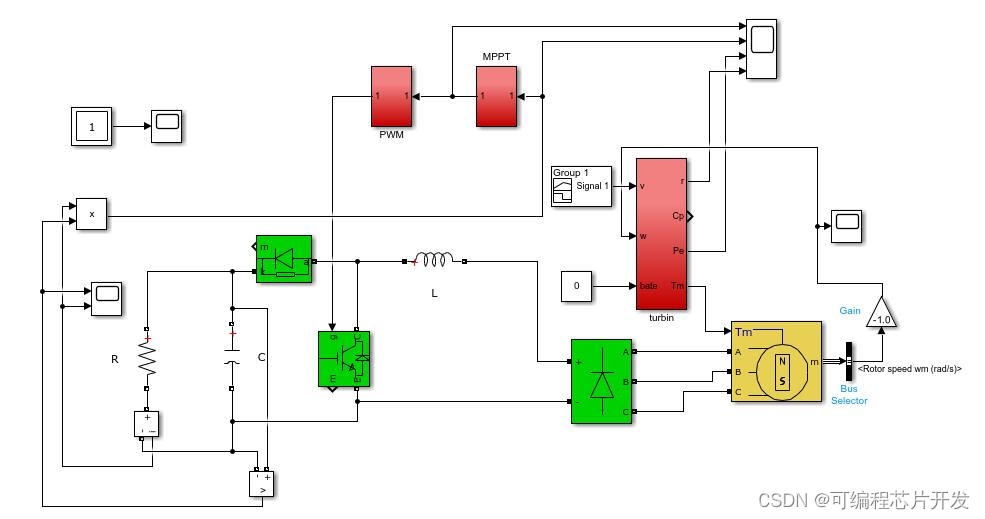
基于MPPT最大功率跟踪算法的涡轮机控制系统simulink建模与仿真
目录 1.课题概述 2.系统仿真结果 3.核心程序与模型 4.系统原理简介 5.完整工程文件 1.课题概述 基于MPPT最大功率跟踪算法的涡轮机控制系统simulink建模与仿真.mppt采用爬山法实现,仿真输出MPPT控制效果,功率,转速等。 2.系统仿真结果 …...

Hbase和Clickhouse对比简单总结
Hbase和Clickhouse是两种不同的数据库系统,它们各自适用于不同的场景。以下是两者之间的对比: 数据模型: HBase 是一种基于列的存储系统,它适合处理大规模的数据集,特别是那些需要快速随机访问的场景。ClickHouse 则是…...
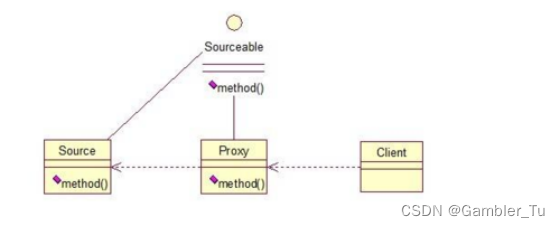
Spring基础之AOP和代理模式
文章目录 理解AOPAOP的实现原理 AOP代理模式静态代理动态代理1-JDK动态代理2-CGLIB动态代理 总结 理解AOP OOP - - Object Oriented Programming 面向对象编程 AOP - - Aspect Oriented Programming 面向切面编程 AOP是Spring提供的关键特性之一。AOP即面向切面编程࿰…...

二层交换机和三层交换机区别
01、二层交换机 二层交换机,也被称为数据链路层交换机,是在OSI模型的数据链路层(第二层)进行数据交换的设备。它基于MAC(Media Access Control)地址来转发数据包,实现局域网内部的数据传输 1、…...
【Java程序设计】【C00267】基于Springboot的在线考试系统(有论文)
基于Springboot的在线考试系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 本系统是基于Springboot的在线考试系统;本系统主要分为管理员、教师和学生三种角色; 管理员登录系统后,可以对首页&#x…...
——代码随想录算法训练营Day41)
【LeetCode】416. 分割等和子集(中等)——代码随想录算法训练营Day41
题目链接:416. 分割等和子集 题目描述 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释&#x…...

51单片机学习(4)-----独立按键进一步控制LED灯
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 目录 一. 独立按键灵活控制LED 程序一:单个独立按键控制多个…...

Redis 学习笔记 3:黑马点评
Redis 学习笔记 3:黑马点评 准备工作 需要先导入项目相关资源: 数据库文件 hmdp.sql后端代码 hm-dianping.zip包括前端代码的 Nginx 启动后端代码和 Nginx。 短信登录 发送验证码 PostMapping("code") public Result sendCode(RequestP…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
代理服务器-LVS的3种模式与调度算法
作者介绍:简历上没有一个精通的运维工程师。请点击上方的蓝色《运维小路》关注我,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 我们上一章介绍了Web服务器,其中以Nginx为主,本章我们来讲解几个代理软件:…...
