神经网络系列---感知机(Neuron)
文章目录
- 感知机(Neuron)
- 感知机(Neuron)的决策函数可以表示为:
- 感知机(Neuron)的学习算法主要包括以下步骤:
- 感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。
感知机(Neuron)
感知机(Neuron)是一种简单而有效的二分类算法,用于将输入数据划分为两个类别。它是机器学习中最早的分类算法之一,由罗森布拉特(Rosenblatt)在1957年提出。
感知机(Neuron)的基本思想是通过一个决策函数将输入数据映射到特定的输出类别。它通过对输入向量进行加权求和,并将结果传递给一个激活函数来产生输出。感知机(Neuron)的学习过程主要涉及确定合适的权重,以便对不同的输入样本进行正确的分类。
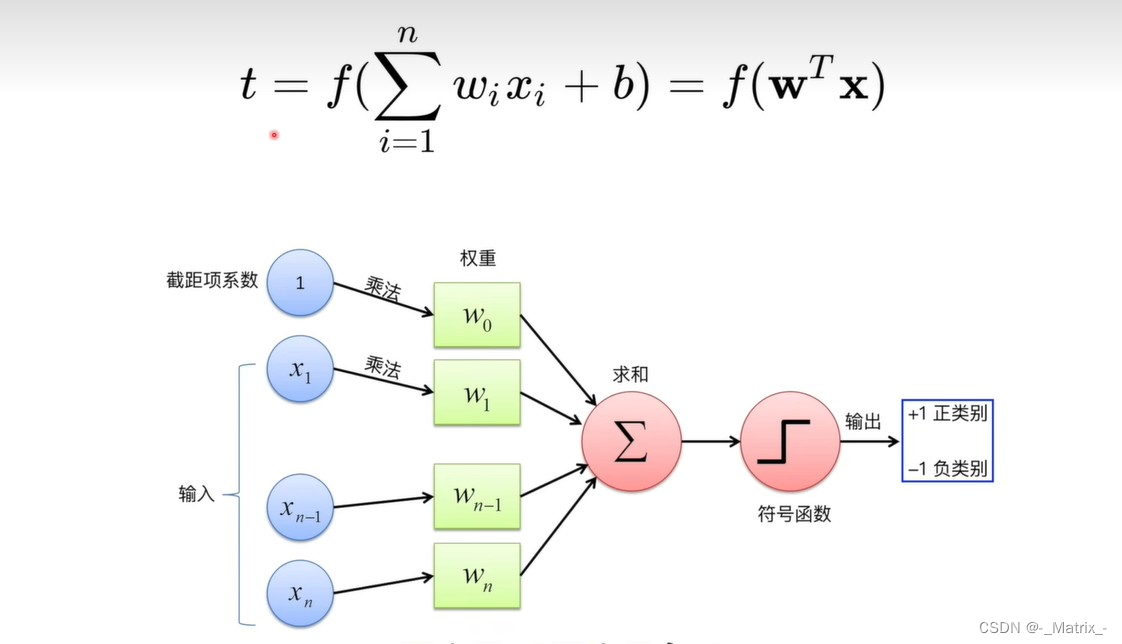
感知机(Neuron)的决策函数可以表示为:
f(x) = sign(w * x + b)sign(x) = {+1, if x >= 0,-1, if x < 0}
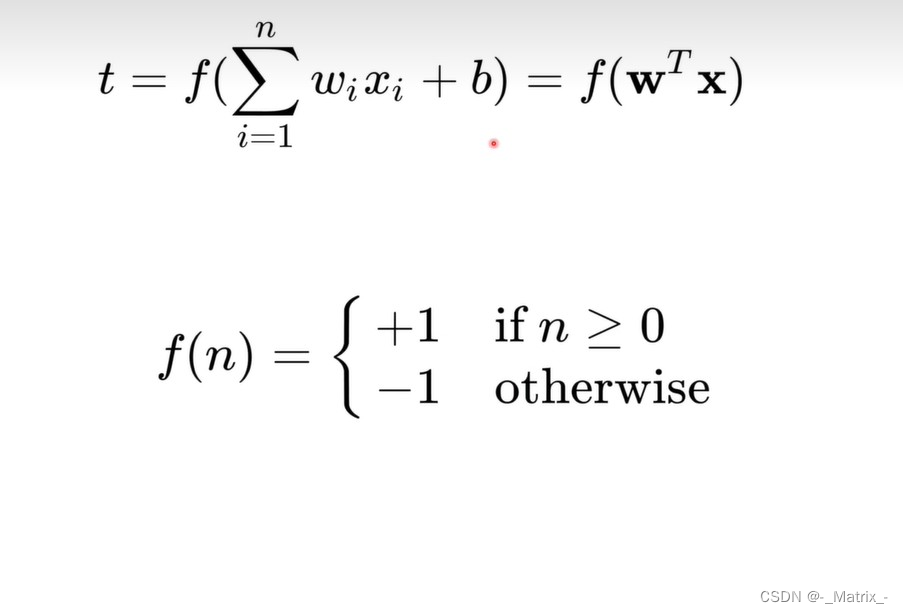
它将大于等于0的值映射为+1,小于0的值映射为-1。在感知机(Neuron)中,"sign"函数被用于判断输入的加权和是否超过了某个阈值,从而确定输入被分类为哪个类别。
其中,x是输入向量,w是权重向量,b是偏置项,sign是符号函数,将输入的实数映射为+1或-1,表示两个不同的类别。
感知机(Neuron)的学习算法主要包括以下步骤:
- 初始化权重向量和偏置项。
- 针对训练数据中的每个样本,计算决策函数的输出。
- 根据实际输出和期望输出之间的差异,更新权重向量和偏置项。
- 重复步骤2和步骤3,直到所有训练样本都被正确分类或达到停止条件。
需要注意的是,感知机(Neuron)只适用于线性可分的问题,即可以通过一个超平面将两个类别的数据完全分开。对于线性不可分的问题,感知机(Neuron)算法无法收敛。
虽然感知机(Neuron)算法在解决简单分类问题上很有用,但它对于复杂问题的处理能力有限。后续发展出了更多强大的分类算法,如支持向量机(Support Vector Machine)和神经网络(Neural Networks)。
y=ax+c ==> ax +(-y)+c =0 //表示一条线 一维形式z=ax+by+d ==> ax +by+(-z)+d =0 //表示一个平面 二维形式
类似于神经网络中的 权重和偏置
ax +by+c =0 //表示所有数据都在这一条线上
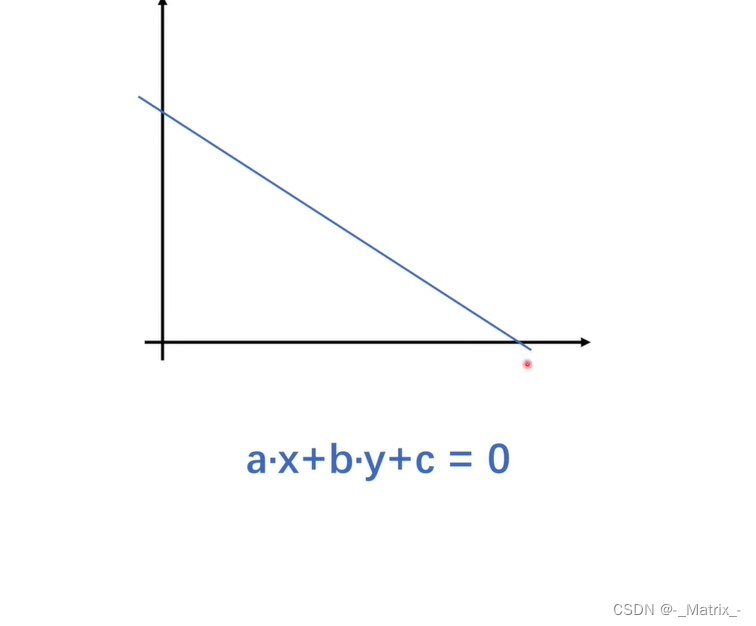
ax +by+c > 0 //表示所有数据都在这一条线的上方
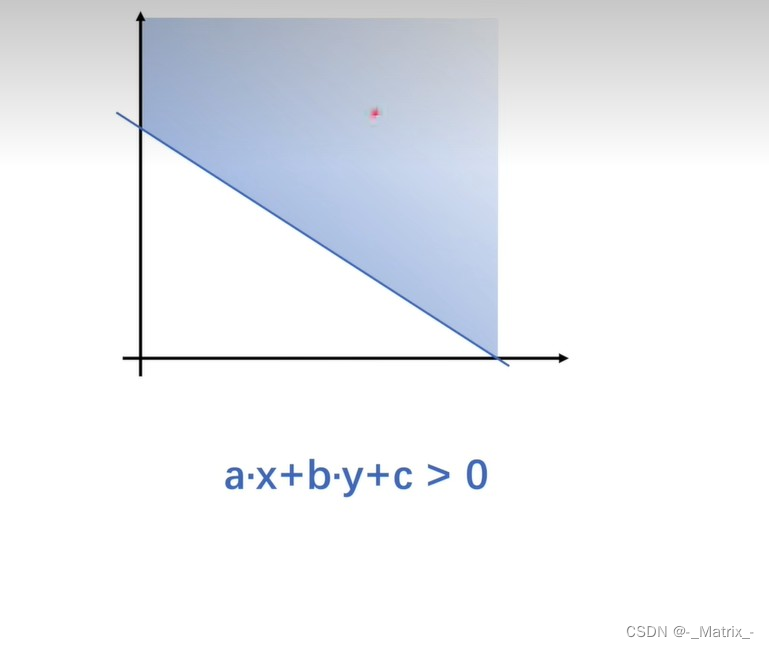
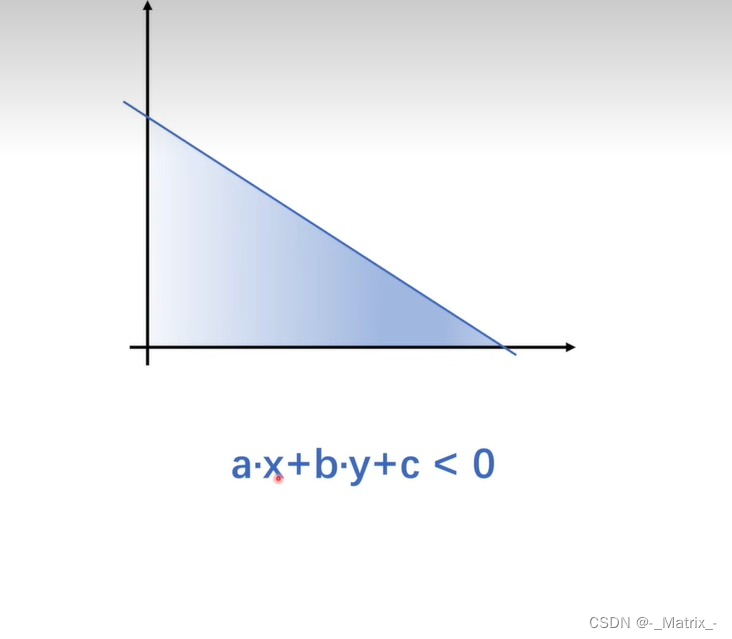
ax +by+c < 0 //表示所有数据都在这一条线的上下方
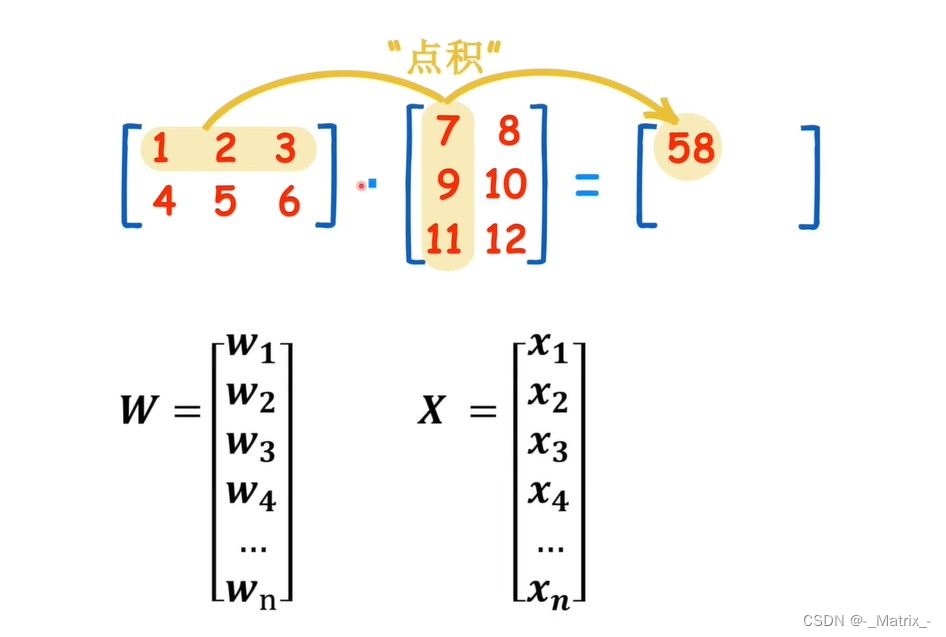
多维度表示:相乘在相加
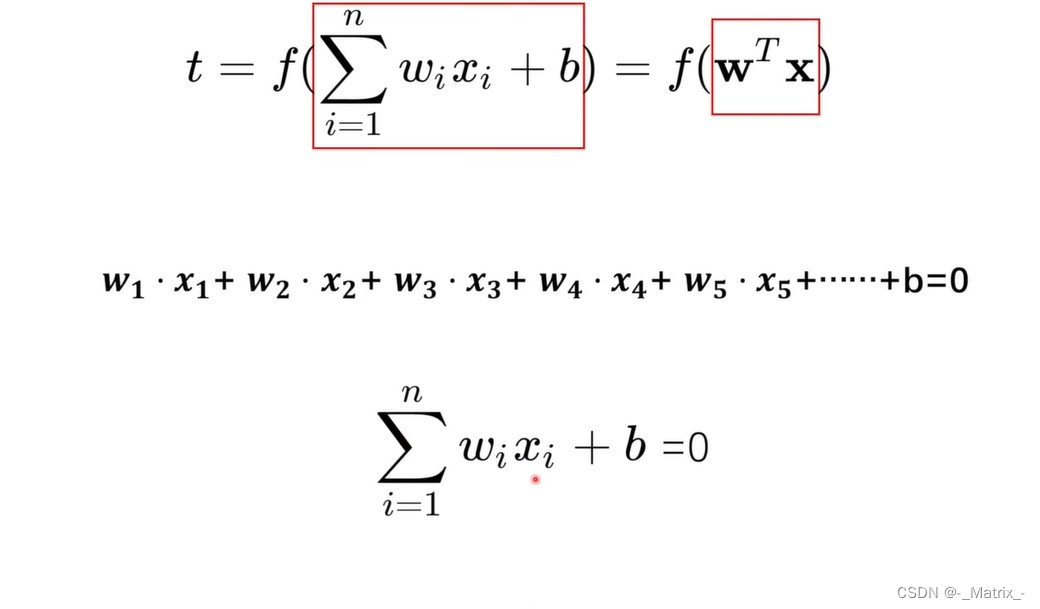
用矩阵表示
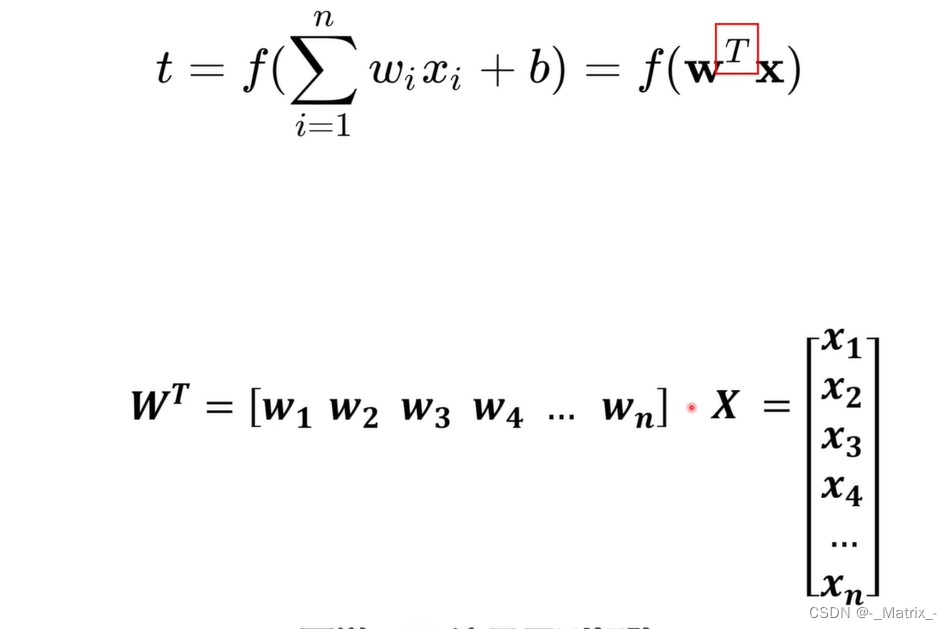

下面用感知机(Neuron) 表达 与(AND)、 或(OR) 、非(NOT) 、异或(XOR) 、 运算。
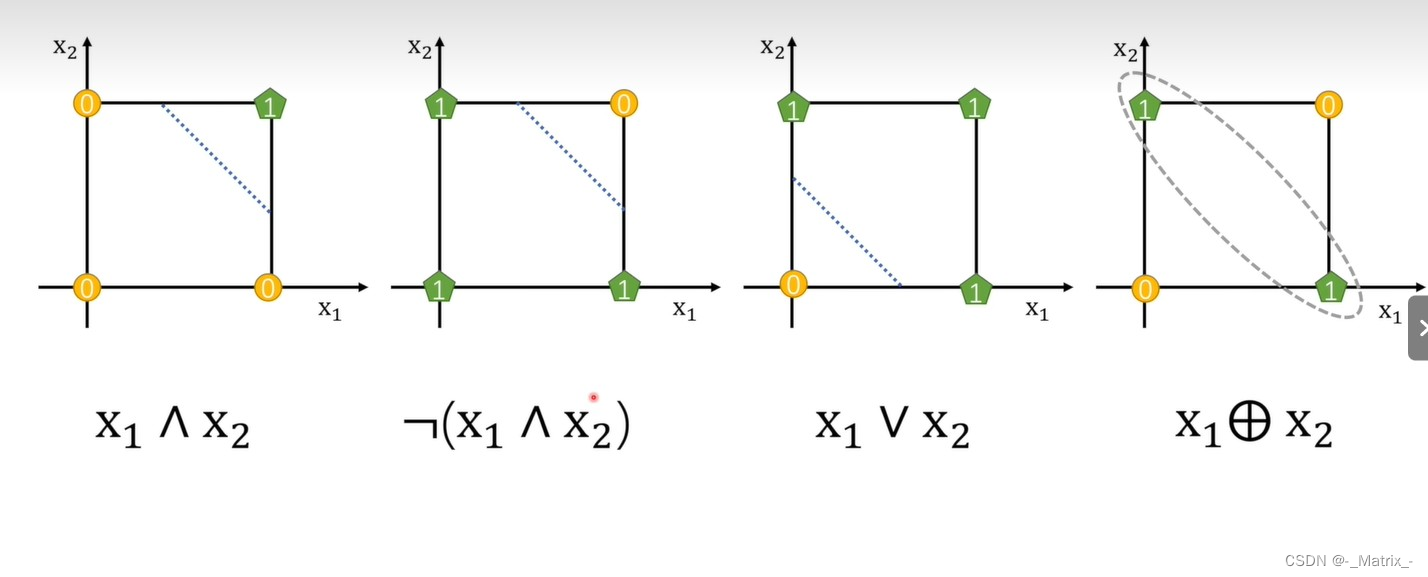
感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。
这里我将为你详细说明如何使用感知机实现这些逻辑运算。
- AND运算:
AND运算是一个二元运算,当且仅当两个输入都为1时,输出为1,否则输出为0。使用感知机可以实现AND运算,具体步骤如下:
- 设置权重向量为 w = [1, 1],偏置项为 b = -1.5。
- 对于输入向量 x = [x1, x2],计算加权和:z = w * x + b。
- 使用符号函数(sign)作为激活函数,即 f(x) = sign(z)。也就是f(x) = sign(x1 + x2 - 1.5),其中sign函数将大于等于0的值映射为1,小于0的值映射为-1。
- 当且仅当 f(x) = 1 时,表示 AND 运算结果为真,否则为假。
- OR运算:
OR运算也是一个二元运算,当两个输入中至少一个为1时,输出为1,否则输出为0。使用感知机可以实现OR运算,具体步骤如下:
- 设置权重向量为 w = [1, 1],偏置项为 b = -0.5。
- 对于输入向量 x = [x1, x2],计算加权和:z = w * x + b。
- 使用符号函数(sign)作为激活函数,即 f(x) = sign(z)。也就是f(x) = sign(x1 + x2 - 0.5),其中sign函数将大于等于0的值映射为1,小于0的值映射为-1。
- 当且仅当 f(x) = 1 时,表示 OR 运算结果为真,否则为假。
- NOT运算:
NOT运算是一个一元运算,当输入为1时,输出为0,当输入为0时,输出为1。使用感知机可以实现NOT运算,具体步骤如下:
- 设置权重向量为 w = [-1],偏置项为 b = 0.5。
- 对于输入 x,计算加权和:z = w * x + b。
- 使用符号函数(sign)作为激活函数,即 f(x) = sign(z)。也就是f(x) = sign( -x + 0.5),其中sign函数将大于等于0的值映射为1,小于0的值映射为-1。
- 当且仅当 f(x) = 1 时,表示 NOT 运算结果为真,否则为假。
异或运算 一个感知机无法实现
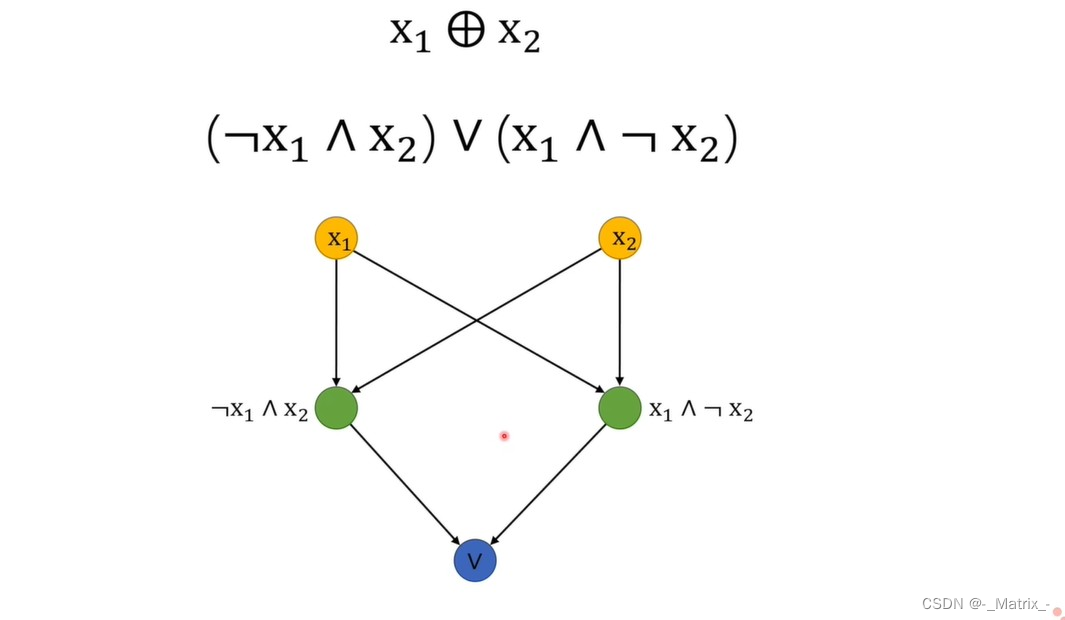
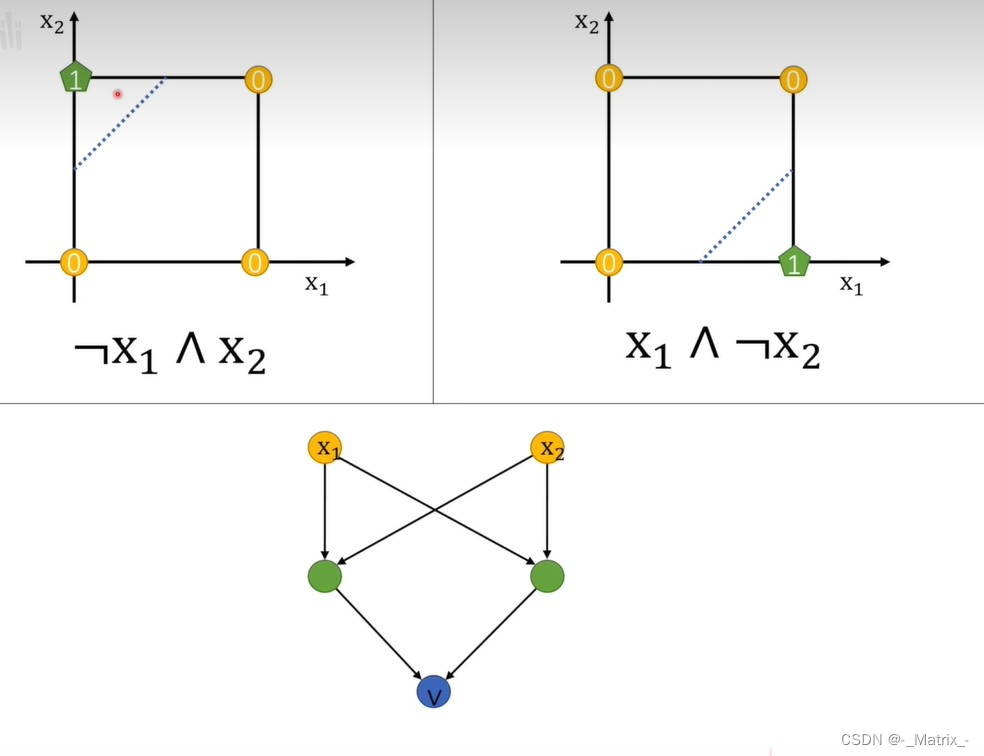
- 描述上图 异或(XOR)运算:
异或运算是一个二元运算,当两个输入相同时,输出为0;当两个输入不同时,输出为1。使用单个感知机无法直接实现异或运算,因为它不是线性可分的。但可以通过组合多个感知机实现。具体步骤如下:
一种常用的方法是使用两个感知机构建一个多层感知机(Multi-Layer Perceptron,MLP)。MLP由输入层、隐藏层和输出层组成,每个层都由多个感知机(神经元)组成。以下是使用MLP实现异或运算的具体步骤:
- 构建输入层和隐藏层:
- 输入层有两个神经元,表示输入的两个二进制位
(x1和x2)。 - 隐藏层有两个神经元,用于引入非线性映射,帮助解决异或运算的非线性可分性。
- 设置隐藏层的权重和偏置项:
-
第一个隐藏层神经元,先对
x1进行非(NOT)运算,也就是0为1,非0为0。 -
然后再进行
与(AND)运算。(h1)的权重向量为 w1 = [1, 1],偏置项为 b1 = -1.5。即:f(x) = sign(x1 + x2 - 1.5)。 -
第二个隐藏层神经元,先对
x2进行非(NOT)运算,也就是0为1,非0为0。 -
然后再进行
与(AND)运算。(h2)的权重向量为 w2 = [1, 1],偏置项为 b2 = -1.5。即:f(x) = sign(x1 + x2 - 1.5)。
- 设置输出层的权重和偏置项:
- 输出层有一个神经元(y),表示异或运算的结果。
- 输出层进行
或(OR)运算,权重向量为 w3 = [1, 1],偏置项为 b3 = -0.5。
- 计算前向传播:
- 对于输入向量 x = [x1, x2],首先计算隐藏层神经元的输出:
h1 = sign(w1 * x + b1)
h2 = sign(w2 * x + b2) - 然后,将隐藏层神经元的输出作为输入传递给输出层神经元:
y = sign(w3 * [h1, h2] + b3)
- 输出结果:
- 当 y = 1 时,表示异或运算的结果为真(1)。
- 当 y = -1 时,表示异或运算的结果为假(0)。
通过这样的多层感知机结构和非线性激活函数(如符号函数),可以实现异或运算。这个例子中使用了一个隐藏层,但在实际应用中可能需要更多的隐藏层和神经元来处理更复杂的问题。这种多层感知机结构是神经网络的基础,也被称为前馈神经网络(Feedforward Neural Network)。
5. 第二种 异或(XOR)运算:
异或运算是一个二元运算,当两个输入相同时,输出为0;当两个输入不同时,输出为1。使用单个感知机无法直接实现异或运算,因为它不是线性可分的。但可以通过组合多个感知机实现。具体步骤如下:一种常用的方法是使用两个感知机构建一个多层感知机(Multi-Layer Perceptron,MLP)。MLP由输入层、隐藏层和输出层组成,每个层都由多个感知机(神经元)组成。以下是使用MLP实现异或运算的具体步骤:1. 构建输入层和隐藏层:
- 输入层有两个神经元,表示输入的两个二进制位(x1和x2)。
- 隐藏层有两个神经元,用于引入非线性映射,帮助解决异或运算的非线性可分性。2. 设置隐藏层的权重和偏置项:
- 第一个隐藏层神经元(h1)的权重向量为 w1 = [1, 1],偏置项为 b1 = -0.5。
- 第二个隐藏层神经元(h2)的权重向量为 w2 = [-1, -1],偏置项为 b2 = 1.5。3. 设置输出层的权重和偏置项:
- 输出层有一个神经元(y),表示异或运算的结果。
- 输出层的权重向量为 w3 = [1, 1],偏置项为 b3 = -1.5。4. 计算前向传播:
- 对于输入向量 x = [x1, x2],首先计算隐藏层神经元的输出:h1 = sign(w1 * x + b1)h2 = sign(w2 * x + b2)
- 然后,将隐藏层神经元的输出作为输入传递给输出层神经元:y = sign(w3 * [h1, h2] + b3)5. 输出结果:
- 当 y = 1 时,表示异或运算的结果为真(1)。
- 当 y = -1 时,表示异或运算的结果为假(0)。
相关文章:

神经网络系列---感知机(Neuron)
文章目录 感知机(Neuron)感知机(Neuron)的决策函数可以表示为:感知机(Neuron)的学习算法主要包括以下步骤:感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。 感知机(Neuron) 感知机(Neuron)是一种简单而有效的二分类算法,用于将输入…...

k8s(2)
目录 一.二进制部署k8s 常见的K8S安装部署方式: k8s部署 二进制与高可用的区别 二.部署k8s 初始化操作: 每台node安装docker: 在 master01 节点上操作; 准备cfssl证书生成工具:: 执行脚本文件: 拉入etcd压缩包…...
利用nginx内部访问特性实现静态资源授权访问
在nginx中,将静态资源设为internal;然后将前端的静态资源地址改为指向后端,在后端的响应头部中写上静态资源地址。 近期客户对我们项目做安全性测评,暴露出一些安全性问题,其中一个是有些静态页面(*.html&…...
fly-barrage 前端弹幕库(1):项目介绍
fly-barrage 是我写的一个前端弹幕库,由于经常在 Bilibili 上看视频,所以对网页的弹幕功能一直蛮感兴趣的,所以做了这个库,可以帮助前端快速的实现弹幕功能。 项目官网地址:https://fly-barrage.netlify.app/ÿ…...

jetcache如果一个主体涉及多个缓存时编辑或者删除时如何同时失效多个缓存
在实际使用过程中,可能会遇到这种情形:一个主体会有多个缓存,比如用户基础信息缓存、用户详情缓存,那么当删除用户信息后就需要同时失效多个缓存中该主体数据,那么jetcache支持这种应用场景么,答案是支持&a…...

uni-app 实现拍照后给照片加水印功能
遇到个需求需要实现,研究了一下后写了个demo 本质上就是把拍完照后的照片放到canvas里,然后加上水印样式然后再重新生成一张图片 代码如下,看注释即可~使用的话记得还是得优化下代码 <template><view class"content"&g…...

【ArcGIS】利用DEM进行水文分析:流向/流量等
利用DEM进行水文分析 ArcGIS实例参考 水文分析通过建立地表水文模型,研究与地表水流相关的各种自然现象,在城市和区域规划、农业及森林、交通道路等许多领域具有广泛的应用。 ArcGIS实例 某流域30m分辨率DEM如下: (1)…...

论文阅读笔记——PathAFL:Path-Coverage Assisted Fuzzing
文章目录 前言PathAFL:Path-Coverage Assisted Fuzzing1、解决的问题和目标2、技术路线2.1、如何识别 h − p a t h h-path h−path?2.2、如何减少 h − p a t h h-path h−path的数量?2.3、哪些h-path将被添加到种子队列?2.4、种…...

C语言中各种运算符用法
C语言中有许多不同的运算符,用于执行各种不同的操作。 以下是C语言中常见的运算符及其用法: 算术运算符: 加法运算符():用于将两个值相加。减法运算符(-):用于将一个值减…...
pythonJax小记(五):python: 使用Jax深度图像(正交投影和透视投影之间的转换)(持续更新,评论区可以补充)
python: 使用Jax深度图像(正交投影和透视投影之间的转换) 前言问题描述1. 透视投影2. 正交投影 直接上代码解释1. compute_projection_parameters 函数a. 参数解释b. 函数计算 2. ortho_to_persp 函数a. 计算投影参数:b. 生成像素坐标网格&am…...
web安全学习笔记【16】——信息打点(6)
信息打点-语言框架&开发组件&FastJson&Shiro&Log4j&SpringBoot等[1] #知识点: 1、业务资产-应用类型分类 2、Web单域名获取-接口查询 3、Web子域名获取-解析枚举 4、Web架构资产-平台指纹识别 ------------------------------------ 1、开源-C…...
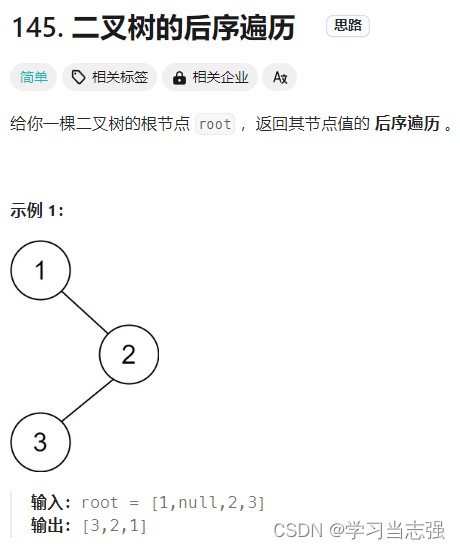
145.二叉树的后序遍历
// 定义一个名为Solution的类,用于解决二叉树的后序遍历问题 class Solution { // 定义一个公共方法,输入是一个二叉树的根节点,返回一个包含后序遍历结果的整数列表 public List<Integer> postorderTraversal(TreeNode root) { /…...

ssh远程连接免密码访问
我们在远程登录的时候,经常需要输入密码,密码往往比较复杂,输入比较耗费时间,这种情况下可以使用ssh免密码登录。 一般的教程是需要生成ssh密钥后,然后把密钥复制到server端完成配置,这里提供一个简单的方…...

Vue-Json-Schema-Form: 如何基于模板定制前端页面
本人从事的是工业物联网, 面对工业设备的通讯难题是各大设备都有各自的通讯协议, 如果想要用一款硬件去和所有设备做通讯的话, 就得面对怎么把自己想要采集的配置下发给自己的采集器的问题, 以前都是采用各种模型去尝试构建配置项, 但是因为配置可能会有深层次嵌套, 而且…...

保存Json对象到数据库
文章目录 背景实现方式1. 直接以 Json 对象保存到数据库2. 以 String 类型保存到数据库 背景 项目过程中可能需要保存 Json 对象到数据库中。 实现方式 有两种实现方式,一种是直接保存 Json 对象到数据库,这种方式在创建实体类以及编写 Mapper XML 脚本…...
《Docker 简易速速上手小册》第3章 Dockerfile 与镜像构建(2024 最新版)
文章目录 3.1 编写 Dockerfile3.1.1 重点基础知识3.1.2 重点案例:创建简单 Python 应用的 Docker 镜像3.1.3 拓展案例 1:Dockerfile 优化3.1.4 拓展案例 2:多阶段构建 3.2 构建流程深入解析3.2.1 重点基础知识3.2.2 重点案例:构建…...
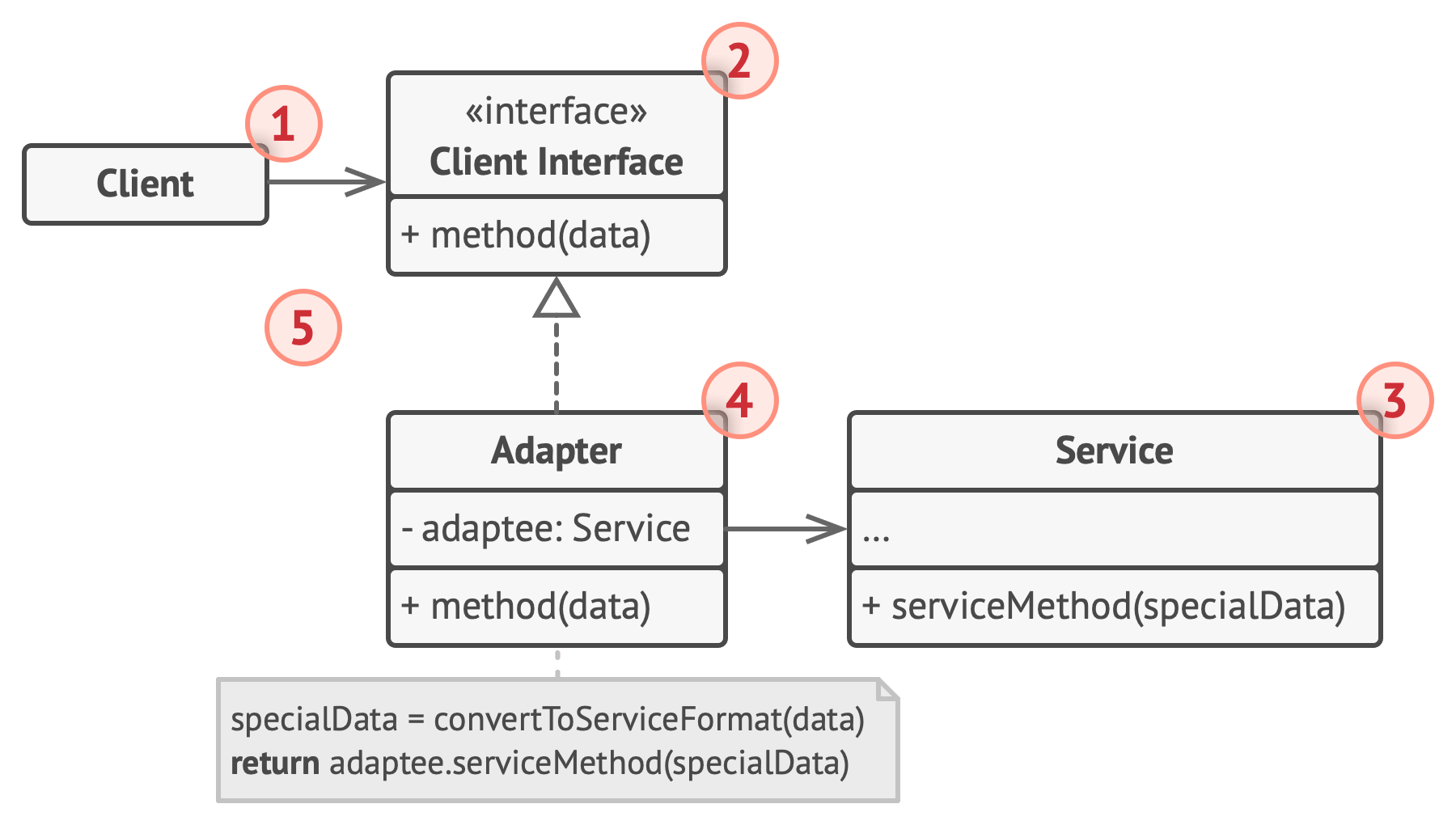
【Python笔记-设计模式】适配器模式
一、说明 适配器模式是一种结构型模式,它使接口不兼容的对象能够相互合作 (一) 解决问题 主要解决接口不兼容问题 (二) 使用场景 当系统需要使用现有的类,但类的接口不符合需求时当需要一个统一的输出接口,但输入类型不可预知时当需要创…...

二分算法(c++版)
二分的本质是什么? 很多人会认为单调性是二分的本质,但其实其本质并非单调性,只是说,有单调性的可以进行二分,但是有些题目没有单调性我们也可以进行二分。其本质其实是一个边界问题,给定一个条件…...

【C#】用于基于 UV DLP 的 3D 打印机的切片软件源码解析(一)DLP原理 GUI
0. 原理 基于 UV DLP 的 3D 打印机的工作原理是这样的: UV DLP 是一种使用数字光处理(Digital Light Processing)技术的 3D 打印方法,它利用紫外光(UV)来固化液态树脂,从而形成实体物体。UV DLP…...

Javase补充-Arrays类的常用方法汇总
文章目录 一 . 排序方法二 . 查找方法三 . 判断是否相等的方法四 . 拷贝方法五 . 填充方法 一 . 排序方法 我们第一个要介绍的就是sort方法 这个排序实现的底层逻辑应该是十分复杂的,以我们目前的水平体系应该无法理解,我们今天尝试用我们可以理解的一种排序算法,插入排序来模…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
