服务区智慧公厕
在如今追求智能化、便捷化的社会背景下,高速公路服务区智慧公厕正成为人们关注的焦点。作为高速公路上的必要设施,公厕的提升已经不再局限于简单的清洁卫生,而是更多地涉及到智能化、舒适度和用户体验。本文以智慧公厕源头厂家广州中期科技有限公司,大量精品案例项目,包括黄山服务区、龙游服务区、泾县服务区等超高端智慧卫生间项目,实景实图解读服务区智慧公厕的特点。
首先,智慧公厕的建设离不开科技的支撑。现代技术的运用让公厕变得更加智能化,在公厕的入口处安装智能感应的无接触开关门设备,(@ZonTree中期科技)能够自动开启、关闭门窗,实现触碰即用,无需直接接触公共设施。公厕内部还配备智能洗手台和更换感应纸巾机,避免了因直接接触带来的交叉感染风险,提升了使用的便捷性和卫生标准。
其次,服务区智慧公厕注重舒适度。感应取纸机、感应洗手液机、感应垃圾桶、感应烘手机、感应照明系统、感应通风换气设备、感应水龙头、感应开关门装置、感应背景音乐等,让用户在使用公厕时能够感受到家的温暖。(@ZonTree中期科技)而且通过智慧公厕云管理平台,实现公共厕所的环境监测与调控、厕位占用监测与引导、消耗品监测与缺失提示、安全防范与管理、自动化清洁与服务、跨区域跨平台的远程监测控等管理功能,大大提升服务区智慧公厕的管理效率。
再者,公厕的环保节能也是智慧公厕的重要特点之一。智慧公厕采用节能环保的照明系统和水电设备,降低了资源的浪费和能源的消耗。(@ZonTree中期科技)一些智慧公厕还配备了环保节能的粪便处理系统,包括真空粪便处理系统和生物降解粪便处理系统,为环境保护做出了贡献。
综上所述,服务区智慧公厕的建设不仅关乎公共卫生和用户体验,更体现了现代科技在生活中的应用和环境保护的重要性。随着科技的不断发展,智慧公厕必将成为未来服务区的新风向,给人们带来更加便捷、舒适和环保的使用体验。




相关文章:

服务区智慧公厕
在如今追求智能化、便捷化的社会背景下,高速公路服务区智慧公厕正成为人们关注的焦点。作为高速公路上的必要设施,公厕的提升已经不再局限于简单的清洁卫生,而是更多地涉及到智能化、舒适度和用户体验。本文以智慧公厕源头厂家广州中期科技有…...

mysql数据库 - 统诉
1、DDL - 数据库操作 show databases; create database 数据库名 use 数据库名 select database() drop database 数据库名 2、DDL- 表操作 show tables; create table desc 表名 show create table 表名 alter table 表名 add/modify/change/rename drop table 表名 3、DML …...

Python入门必学:单引号、双引号与三引号的差异与应用
Python入门必学:单引号、双引号与三引号的差异与应用 🌈 个人主页:高斯小哥 🔥 高质量专栏:Matplotlib之旅:零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程 👈 希望得…...

spring缓存的使用
Spring缓存使用 缓存注解 对于Spring,缓存组件例如EhCache是可拔插的,而缓存注解是通用的。 Cacheable 标记在方法或者类上,标识该方法或类支持缓存。Spring调用注解标识方法后会将返回值缓存到redis,以保证下次同条件调用该方…...
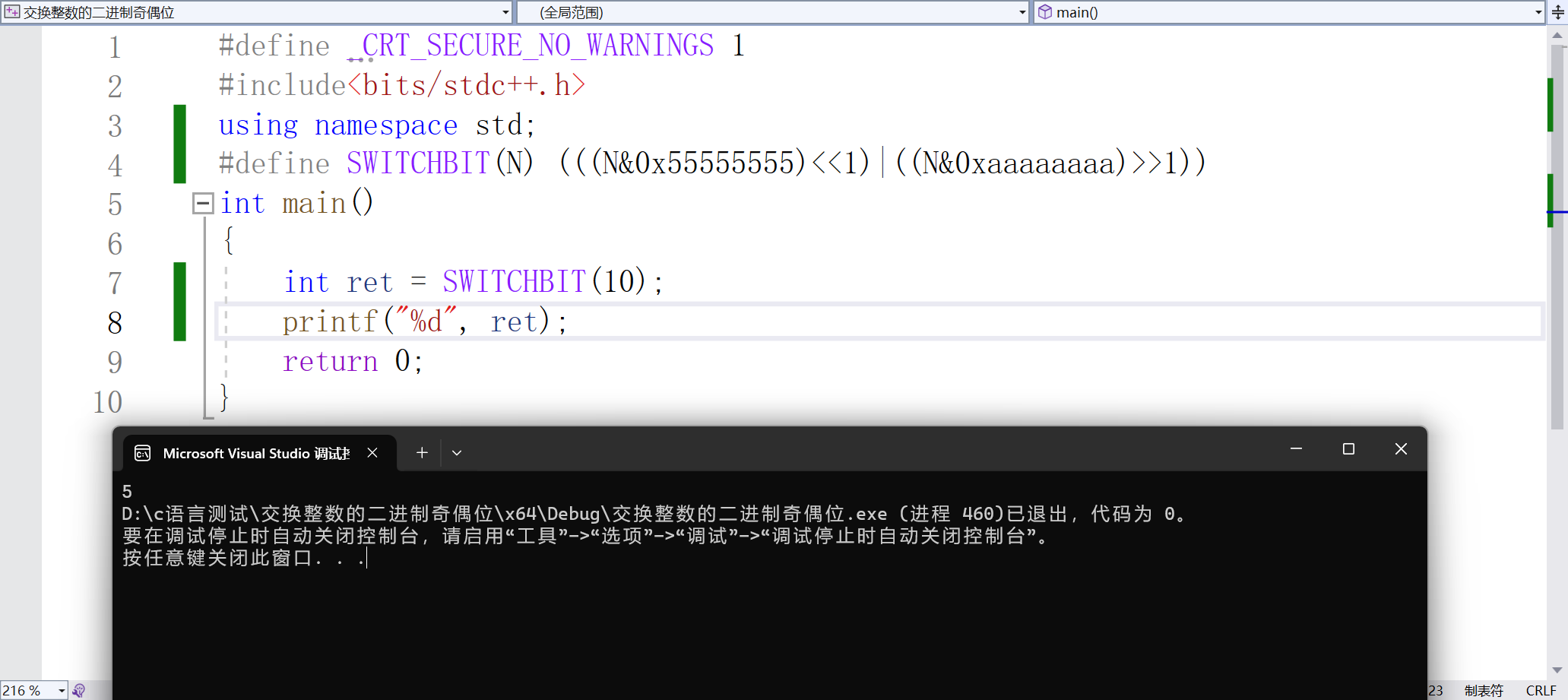
交换整数的二进制奇偶位
题目:写一个宏,可以将一个整数的二进制位的奇数位和偶数位交换。 假设我们举例:10 那么他的二进制就是:00000000 00000000 00000000 00001010 交换以后组成的新的数就是 5 怎么用写这个宏呢? 1.分别拿出奇数位和偶数位…...

在做了frp的实验室服务器不同端口间传输文件
背景 实验室有两台服务器,使用的是一个IP,两个端口,给人看上去是一台服务器的两个端口,实际是两台服务器。 现在我需要从一个端口传输一个文件夹到另外一个端口,实际上是从一个机器传输到另外一个机器。 操作 在两台…...
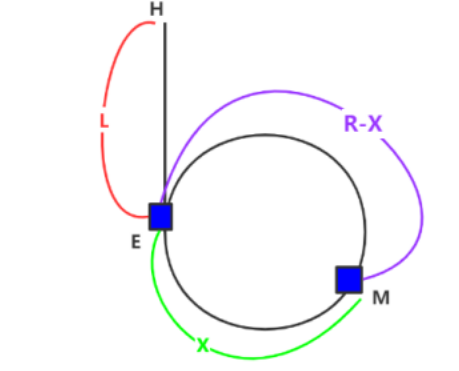
数据结构链表力扣例题AC(3)——代码以及思路记录
160. 相交链表 给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。 AC写法一 struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {//思…...
C++初阶:容器适配器priority_queue常用接口详解及模拟实现、仿函数介绍
介绍完了stack和queue的介绍以及模拟的相关内容后:C初阶:容器适配器介绍、stack和queue常用接口详解及模拟实现 接下来进行priority_queue的介绍以及模拟: 文章目录 1.priority_queue的介绍和使用1.1priority_queue的初步介绍1.2priority_que…...

提取淘宝店铺联系方式的爬虫工具
随着电子商务的快速发展,淘宝成为了许多人购物的首选平台。而对于一些商家来说,获取淘宝店铺的联系方式是非常重要的,以便建立更加直接和有效的沟通渠道。本文将介绍一种基于Python的爬虫工具,可以帮助我们提取淘宝店铺的联系方式…...

Eureka服务搭建
1️⃣搭建服务 引入依赖 <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-netflix-eureka-server</artifactId></dependency>启动类加注解 EnableEurekaServer SpringBootApplication public…...

SORA技术报告
文档链接:https://openai.com/research/video-generation-models-as-world-simulators 文章目录 Video generation models as world simulatorsTurning visual data into patchesVideo compression networkSpacetime latent patchesScaling transformers for video …...

Python Web开发记录 Day1:HTML
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 一、HTML1、前端引入和HTML标签①前端引入②浏览…...

六、回归与聚类算法 - 模型保存与加载
目录 1、API 2、案例 欠拟合与过拟合线性回归的改进 - 岭回归分类算法:逻辑回归模型保存与加载无监督学习:K-means算法 1、API 2、案例...
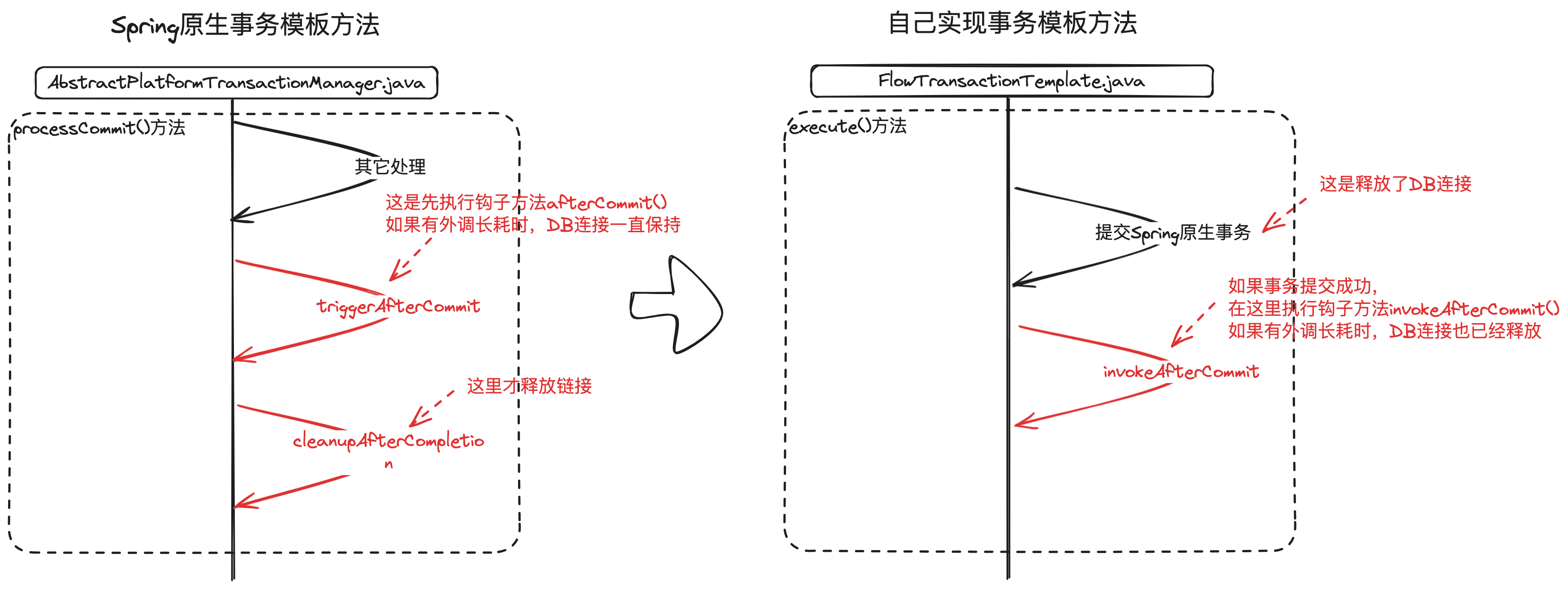
Spring事务模板及afterCommit存在的坑
大家好,我是墨哥(隐墨星辰)。今天的内容来源于两个线上问题,主要和大家聊聊为什么支付系统中基本只使用事务模板方法,而不使用声明式事务Transaction注解,以及使用afterCommit()出现连接未按预期释放导致的…...
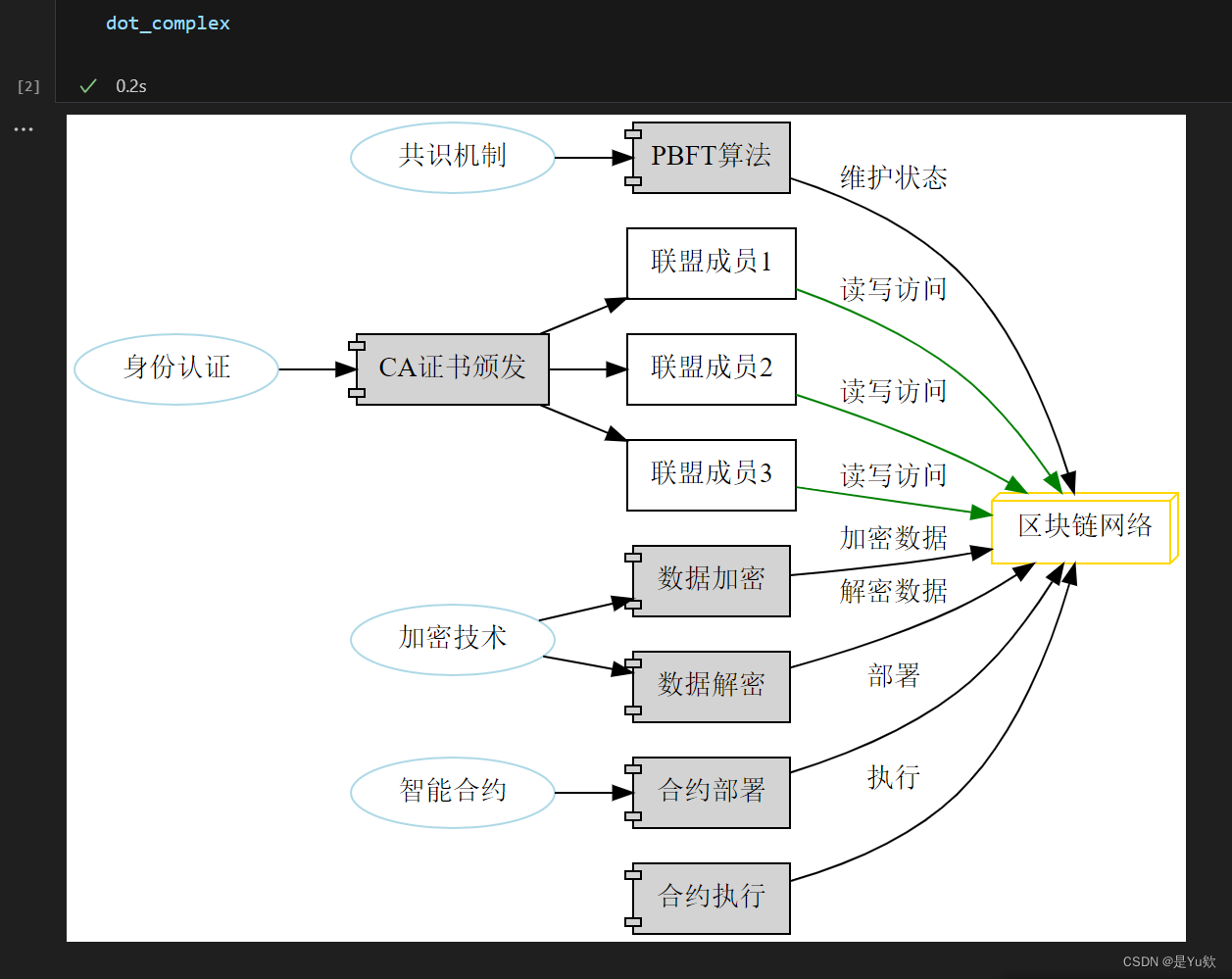
【区块链】联盟链
区块链中的联盟链 写在最前面**FAQs** 联盟链:区块链技术的新兴力量**联盟链的定义****联盟链的技术架构**共识机制智能合约加密技术身份认证 **联盟链的特点**高效性安全性可控性隐私保护 **联盟链的应用场景****金融服务****供应链管理****身份验证****跨境支付**…...

Oracle case when end和decode的区别
Oracle中的CASE WHEN和DECODE都是条件表达式,但它们在某些方面有所不同。 CASE WHEN: CASE WHEN是一个条件表达式,允许您基于条件返回不同的值。它具有以下结构: sql CASE WHEN condition1 THEN result1 WHEN condition2 THE…...

Java导出pdf格式文件
Java实现导出pdf |word |ppt 格式文件 controller层: ApiOperation("导出")GetMapping("/download")public void download(RequestParam("userId") Long userId ,HttpServletResponse response) {reportResul…...
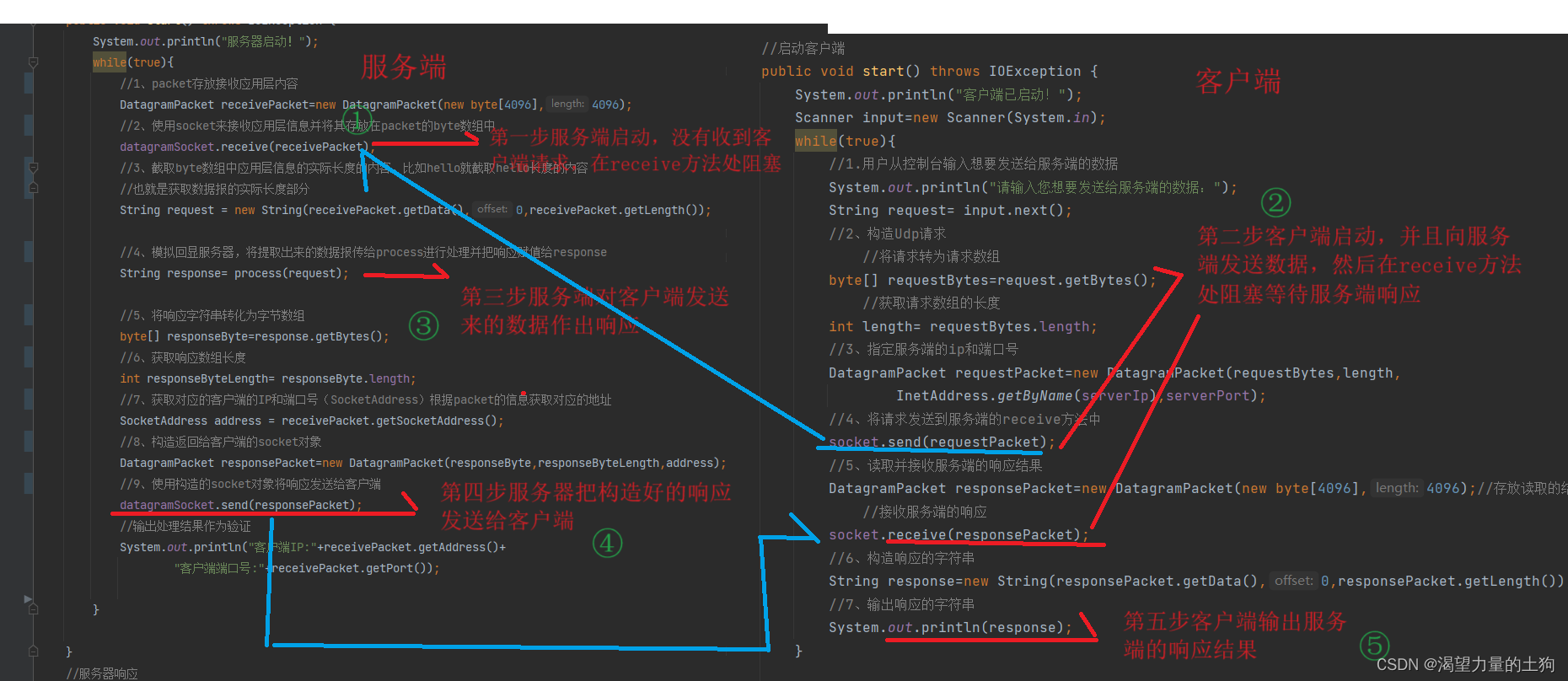
Socket、UDP、TCP协议和简单实现基于UDP的客户端服务端
目录 Socket TCP和UDP区别 UDP:无连接,不可靠传输,面向数据报,全双工 TCP:有连接,可靠传输,面向字节流,全双工 无连接和有连接 可靠传输和不可靠传输 面向数据报和面向字节流…...
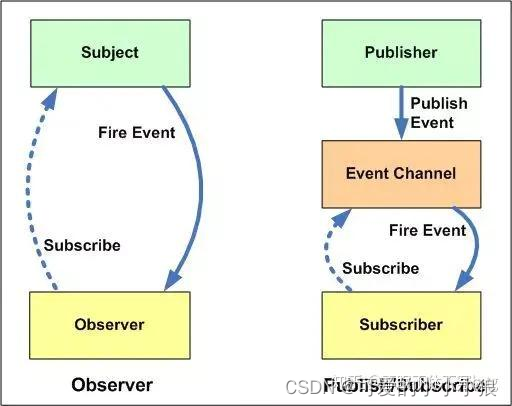
发布订阅模式:观察者模式的一种变体
发布-订阅模型(Publish-Subscribe Model)的底层机制通常基于观察者模式。 发布-订阅模型是观察者模式的一种变体。 在观察者模式中,主题(或被观察者)维护了一组观察者,当主题的状态发生变化时,…...
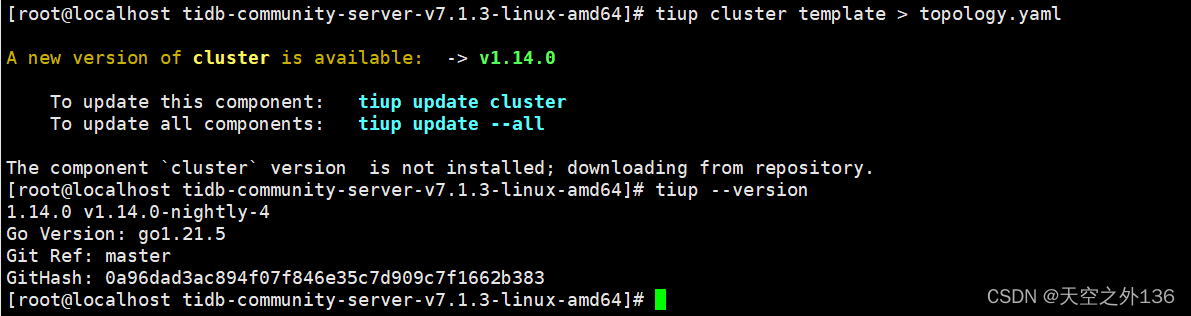
TiDB离线部署、Tiup部署TiDB
先做tidb准备工作: 部署 TiDB 前的环境检查操作:TiDB 环境与系统配置检查 | PingCAP 文档中心 1.查看数据盘 fdisk -l (2,3)本人的分区已经是 ext4 文件系统不用分区,具体官方文档的分区: 4.查看数据盘…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...

【题解-洛谷】P10480 可达性统计
题目:P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M,接下来 M M M 行每行两个整数 x , y x,y x,y,表示从 …...
