LeetCode 第41天 | 背包问题 二维数组 一维数组 416.分割等和子集 动态规划
46. 携带研究材料(第六期模拟笔试)
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
输入描述
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。
输出描述
输出一个整数,代表小明能够携带的研究材料的最大价值。
输入示例
6 1
2 2 3 1 5 2
2 3 1 5 4 3
输出示例
5
提示信息
小明能够携带 6 种研究材料,但是行李空间只有 1,而占用空间为 1 的研究材料价值为 5,所以最终答案输出 5。
数据范围:
1 <= N <= 5000
1 <= M <= 5000
研究材料占用空间和价值都小于等于 1000
思路:纯正的01背包问题
二维数组方法:dp[i][j]中i表示第几个物品,j表示容量[0, n],当背包容量大于当前物品权重时,递推公式为:
dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]),即从左上方推出;
容量小于当前物品权重时直接从上方赋值,即dp[i][j] = dp[i-1][j]。初始化时第一列表示容量为0的最大价值,初始化为0,第一行中如果当前容量大于等于第1个物品的权重value[0]时,初始化为value[0],否则为value[1]。
这样就可以从左上方来推啦。
#include<iostream>
#include<vector>
#include <bits/stdc++.h>
using namespace std;
int solve(int M, int N) {vector<int> weight(M,0);vector<int> value(M,0);for (int i = 0; i<M; i++) {cin>>weight[i];}for (int i = 0; i<M; i++) {cin>>value[i];}vector<vector<int>> dp(M, vector<int>(N+1, 0));for (int j = weight[0]; j<=N; j++) {dp[0][j] = value[0];}for (int i = 1; i<M; i++) {for (int j = 0; j<=N; j++) {if (j < weight[i])dp[i][j] = dp[i-1][j];elsedp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);}}cout<<dp[M-1][N];
}
int main() {int M,N;while(cin>>M>>N){solve(M,N);}return 0;
}
一维dp思路:二维数组压缩成一维数组,即滚动数组,可以节省空间。因为观察递推公式:dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]),可以看到,本行的递推所需数据均在上一行,且均在左侧,因此可以把上一行的数据复制到本行接着使用。因此定义一个dp[n+1]的数组即可保存完毕。dp[j]表示容量为j的最大价值,递推公式类似二维:
dp[j] = max(dp[j], dp[j-weight[i]]+value[i])。可以看到如果其实本质思想还是二维数组,但是巧妙地运用方法使二维数组变为一维数组,节省空间,代码简洁。注意遍历顺序,在二维数组中可以先物品,在容量,亦可以反过来;但是一维由于压缩,只可以先物品,后容量,容量遍历顺序必须从后向前,否则会造成数据覆盖,某些物品权重多加。
// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;int main() {// 读取 M 和 Nint M, N;cin >> M >> N;vector<int> costs(M);vector<int> values(M);for (int i = 0; i < M; i++) {cin >> costs[i];}for (int j = 0; j < M; j++) {cin >> values[j];}// 创建一个动态规划数组dp,初始值为0vector<int> dp(N + 1, 0);// 外层循环遍历每个类型的研究材料for (int i = 0; i < M; ++i) {// 内层循环从 N 空间逐渐减少到当前研究材料所占空间for (int j = N; j >= costs[i]; --j) {// 考虑当前研究材料选择和不选择的情况,选择最大值dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);}}// 输出dp[N],即在给定 N 行李空间可以携带的研究材料最大价值cout << dp[N] << endl;return 0;
}
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
思路:这个题就是寻找两个集合,使其子集的和相等,即各为数组总和的一半。如果使用回溯,就会是指数级的时间复杂度,因此需要用背包问题来看待。物品价值和权重的值相等,总容量为target = sum/2。递推公式为:
dp[j] = max(dp[j], dp[j-nums[i]] + nums[i]);其余循环遍历顺序等和简单01背包相同。最后只需要返回是否可以满足条件,就是判断dp[target] == target的bool值。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;// 计算数组总价值量for (auto num : nums) {sum += num;}// 如果价值量为奇数,不可以平均分成两份,因此必为falseif (sum % 2 == 1) return false;int target = sum / 2;// 初始化dp数组为全0vector<int> dp(target + 1, 0);// 虽然是一维数组做dp但是还是要两层循环,外层表示物品个数,内层表示容量for (int i = 0; i<nums.size(); i++) {for (int j = target; j >= nums[i]; j--) {// 物品的价值和权重时一样的。均为1dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);}}// 如果容量等于dp最后得到的状态值,返回真if (target == dp[target]) {return true;}else {return false;}}
};
相关文章:

LeetCode 第41天 | 背包问题 二维数组 一维数组 416.分割等和子集 动态规划
46. 携带研究材料(第六期模拟笔试) 题目描述 小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实…...
Ubuntu20.04和Windows11下配置StarCraft II环境
1.Ubuntu20.04 根据下面这篇博客就可以顺利安装: 强化学习实战(九) Linux下配置星际争霸Ⅱ环境https://blog.csdn.net/weixin_39059031/article/details/117247635?spm1001.2014.3001.5506 Ubuntu下显示游戏界面目前还没有解决掉。 大家可以根据以下链接看看能…...
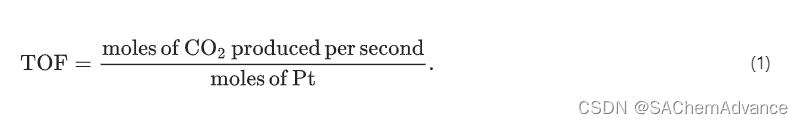
【NCom】:通过高温气相合成调节Pt-CeO2相互作用以提高晶格氧的还原性
摘要:在这项工作中,我们比较了通过两种方法制备的 Pt 单原子催化剂(SAC)的 CO 氧化性能:(1)传统的湿化学合成(强静电吸附strong electrostatic adsorption–SEA)…...

git 将一个分支的提交移动到另一个分支
假设想把分支A上的最后一部分commit移动到分支B之上: 首先切到分支B git checkout B然后执行如下指令,commit id 为A分支上,需要移动的那些提交 git cherry-pick <commit id> ( <commit id> 可多个)中途可能遇到一些…...

vue3 实现 el-pagination页面分页组件的封装以及调用
示例图 一、组件代码 <template><el-config-provider :locale"zhCn"><el-pagination background class"lj-paging" layout"prev, pager, next, jumper" :pager-count"5" :total"total":current-page"p…...
#FPGA(IRDA)
1.IDE:Quartus II 2.设备:Cyclone II EP2C8Q208C8N 3.实验:IRDA(仿真接收一个来自0x57地址的数据0x22 (十进制34)) 4.时序图: 5.步骤 6.代码: irda_receive.v module irda_receive ( input wire…...

Sora—openai最新大模型文字生成视频
这里没办法发视频,发几个图片感受感受吧 OpenAI发布了Sora,一种文字生成视频的技术,从演示看,效果还是相当不错的。 Sora的强大之处在于其能够根据文本描述,生成长达 60秒的视频,其中包含精细复杂的场景…...
介绍(网络电话、ip电话))
VoIP(Voice over Internet Protocol 基于IP的语音传输)介绍(网络电话、ip电话)
文章目录 VoIP(基于IP的语音传输)1. 引言2. VoIP基础2.1 VoIP工作原理2.2 VoIP协议 3. VoIP的优势和挑战3.1 优势3.2 挑战 4. VoIP的应用5. 总结 VoIP(基于IP的语音传输) 1. 引言 VoIP,全称Voice over Internet Prot…...

编程笔记 Golang基础 027 结构体
编程笔记 Golang基础 027 结构体 一、结构体的定义二、结构体的实例化1. 直接初始化2. 使用键值对初始化(即使字段顺序不一致也能正确赋值)3. 部分初始化(未指定的字段会得到它们类型的零值)4. 使用var声明和初始化5. 结构体字面量…...

opencascade15解析导出为step格式
#include "DisplayScene.h" // 包含显示场景的头文件 #include "Viewer.h" // 包含查看器的头文件// OpenCascade 包含 #include <BRepPrimAPI_MakeCylinder.hxx> // 创建圆柱体 #include <BinXCAFDrivers.hxx> // 二进制XCAF驱动程序 #includ…...

【软件设计模式之模板方法模式】
文章目录 前言一、什么是模板方法模式?二、模板方法模式的结构1. 抽象类定义2. 具体实现 三、模板方法模式的应用场景1. 算法重用2. 操作中的固定步骤3. 扩展框架的功能4. 提供回调方法5. 遵循开闭原则 四、模板方法模式的优缺点1. 优点代码复用扩展性好符合开闭原则…...
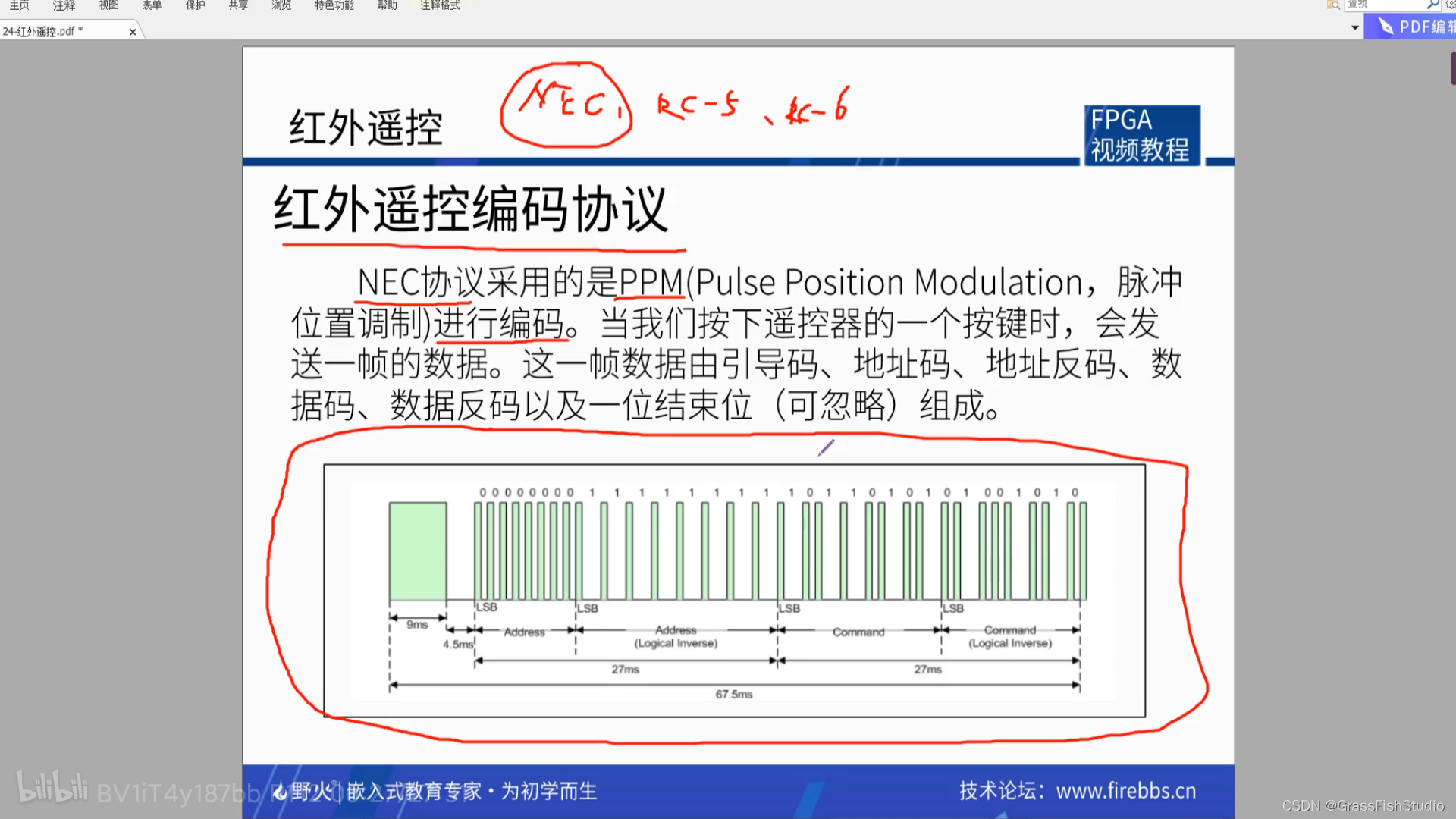
Spring Boot项目怎么对System.setProperty(key, value)设置的属性进行读取加解密
一、前言 之前我写过一篇文章使用SM4国密加密算法对Spring Boot项目数据库连接信息以及yaml文件配置属性进行加密配置(读取时自动解密),对Spring Boot项目的属性读取时进行加解密,但是没有说明对System.setProperty(key, value)设…...
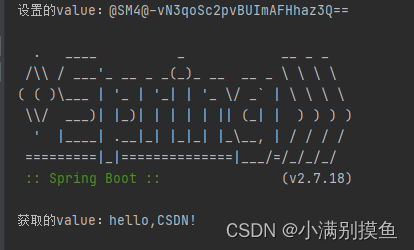
Linux理解
VMware安装Linux安装 目录 VMware安装Linux安装 1.1 什么是Linux 1.2 为什么要学Linux 1.3 学完Linux能干什么 2.1 主流操作系统 2.2 Linux系统版本 VMware安装Linux安装 1.1 什么是Linux Linux是一套免费使用和自由传播的操作系统。 1.2 为什么要学Linux 1). 企业用人…...
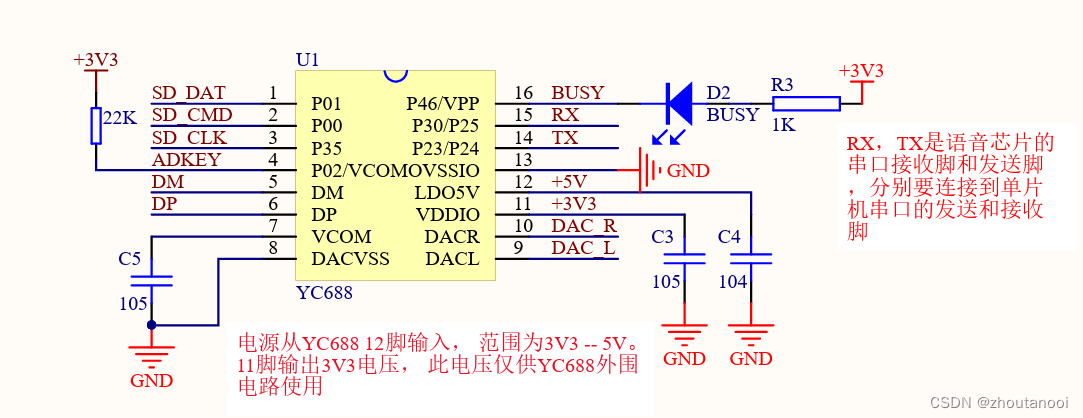
常用芯片学习——YC688语音芯片
YC688 广州语创公司语音芯片 使用说明 YC688是一款工业级的MP3语音芯片 ,完美的集成了MP3、WAV的硬解码。支持SPI-Flash、TF卡、U盘三种存储设备。可通过电脑直接更新SPI-Flash的内容,无需上位机软件。通过简单的串口指令即可完成三种存储设备的音频插…...

C语言:指针的进阶讲解
目录 1. 二级指针 1.1 二级指针是什么? 1.2 二级指针的作用 2. 一维数组和二维数组的本质 3. 指针数组 4. 数组指针 5. 函数指针 6. typedef的使用 7. 函数指针数组 7.1 转移表 1. 二级指针 如果了解了一级指针,那二级指针也是可以很好的理解…...
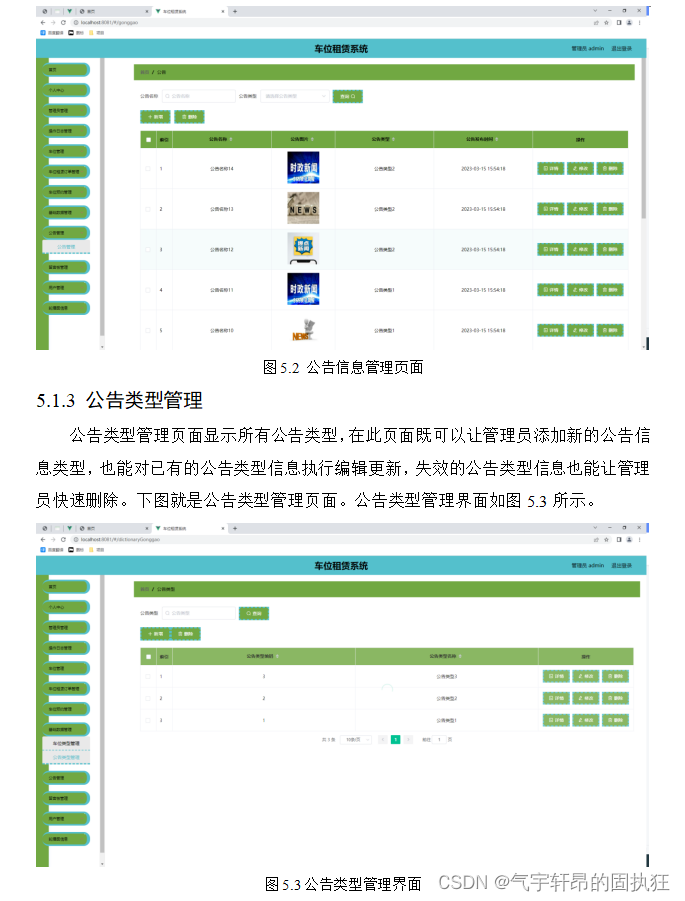
基于SSM的车位租赁系统(有报告)。Javaee项目。ssm项目。
演示视频: 基于SSM的车位租赁系统(有报告)。Javaee项目。ssm项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构,通过Spring Spri…...

Java pyhon C C++ R JS 主流语言的区别-03
以下是对这几种语言的数据类型进行简要归纳: Java的数据类型: 基本数据类型:包括整数类型(byte、short、int、long)、浮点数类型(float、double)、字符类型(char)和布尔…...
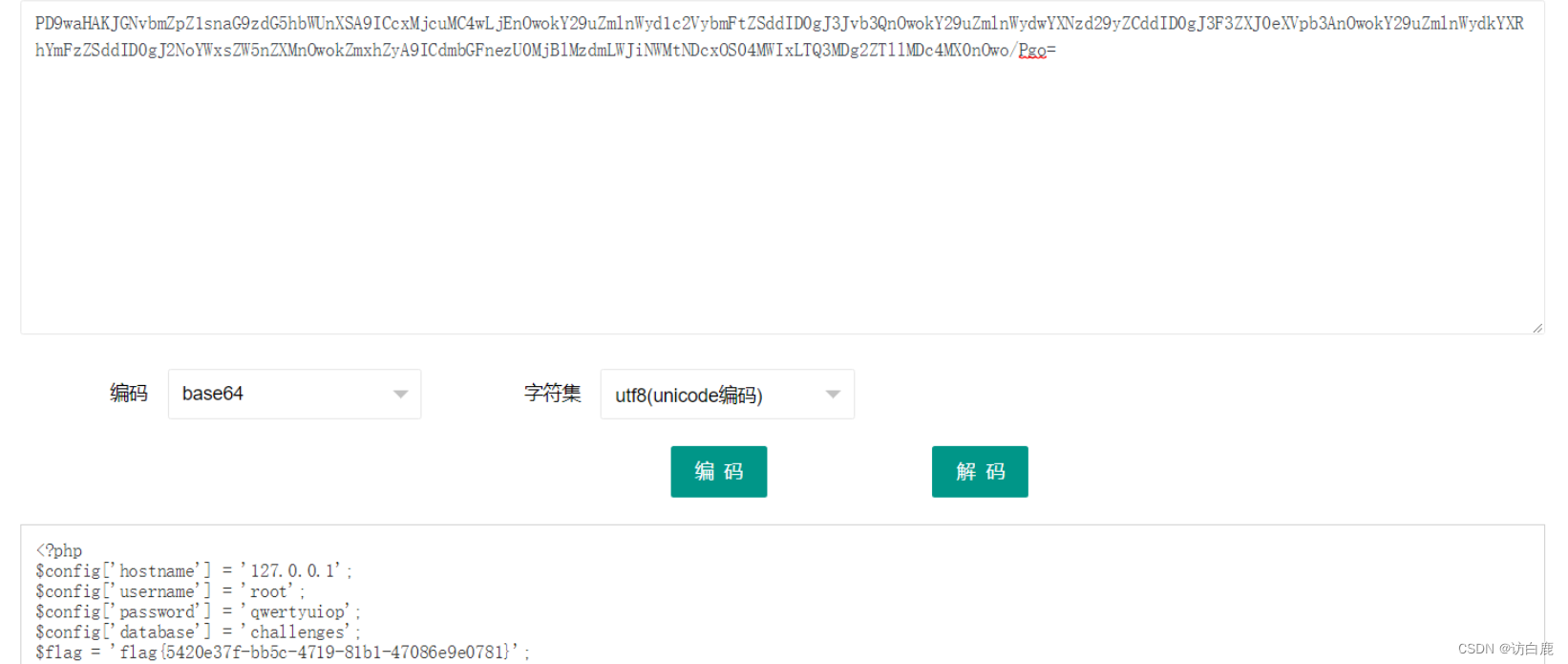
5 buuctf解题
命令执行 [BJDCTF2020]EasySearch1 打开题目 尝试弱口令,发现没有用 扫描一下后台,最后用御剑扫描到了index.php.swp 访问一下得到源码 源码如下 <?phpob_start();function get_hash(){$chars ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstu…...
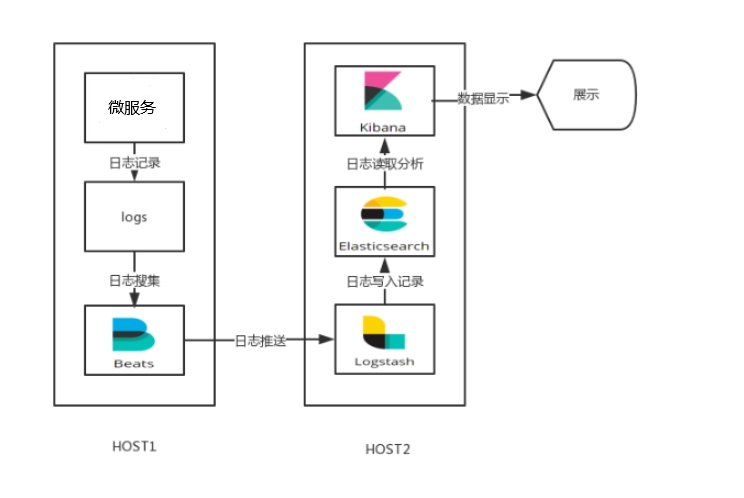
微服务三十五关
1.微服务有什么好处? 微服务优点很多,但是我们通常说一个东西好肯定会跟另一个东西比较, 通常说微服务好会和单体项目进行比较。以下是微服务相对于单体项目的一些显著好处: 首先,让我们讨论单体项目的一些主要缺点&a…...
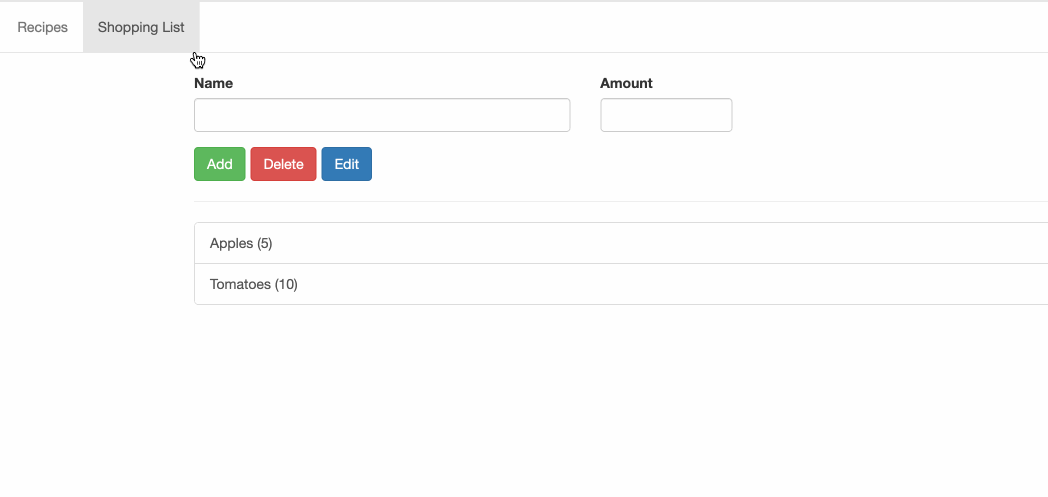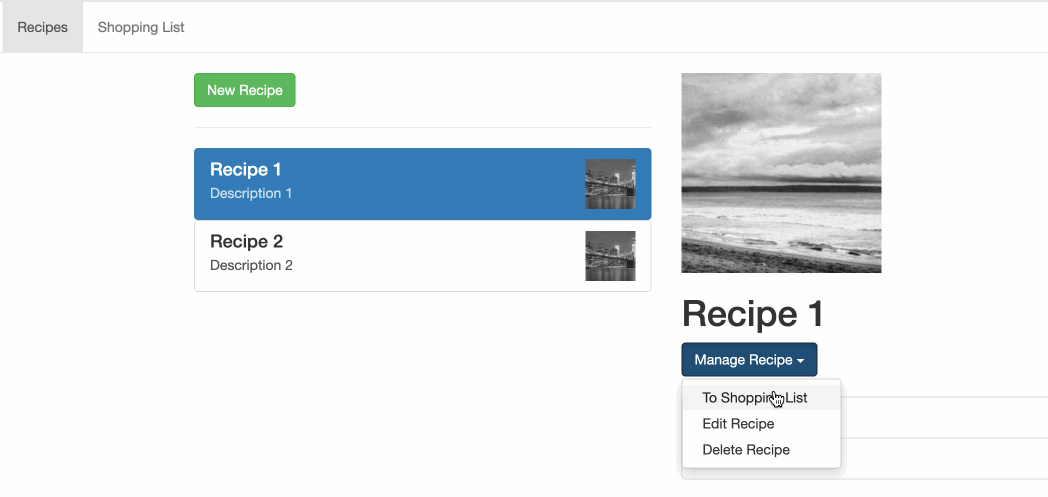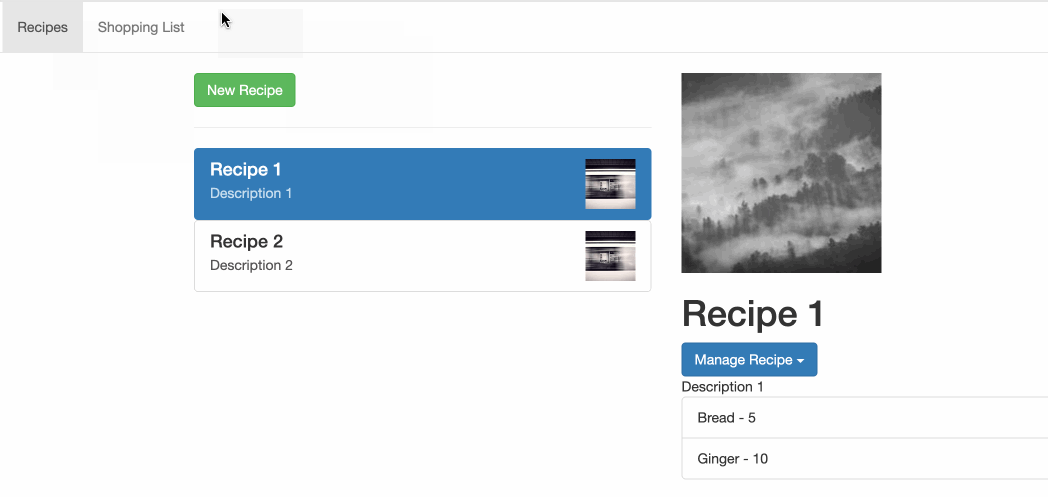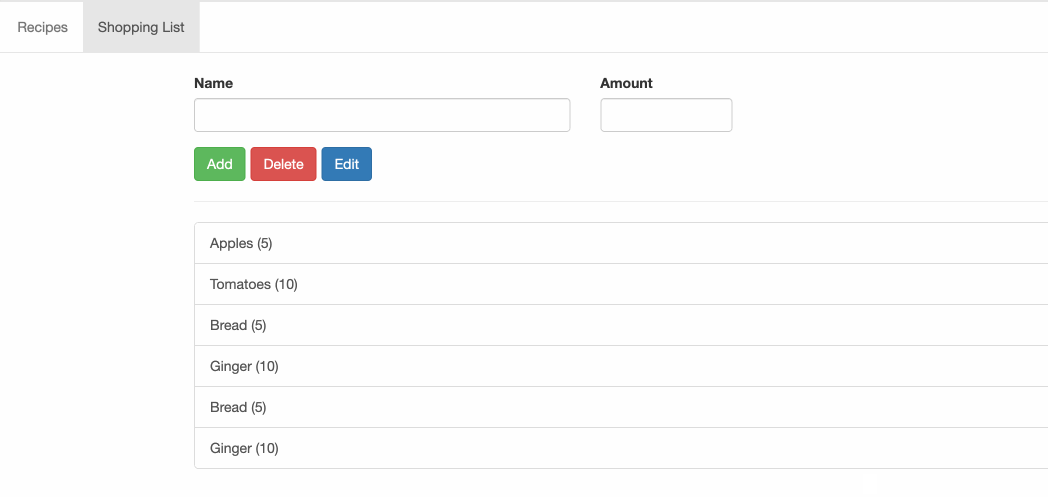
第一个 Angular 项目 - 添加服务
第一个 Angular 项目 - 添加服务 这里主要用到的内容就是 [Angular 基础] - service 服务 提到的 前置项目在 第一个 Angular 项目 - 动态页面 这里查看 想要实现的功能是简化 shopping-list 和 recipe 之间的跨组件交流 回顾一下项目的结构: ❯ tree src/app/…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...
