七、矩阵的初等变换
目录
-1. 介绍
0、增广矩阵:
1、初等变换的性质:
编辑2、矩阵初等变换的分类:
2.1 普通的行阶梯矩阵:
2.2 、行最简形矩阵:
2.3、标准形矩阵:
3、初等变换的定理:
4、初等变换的应用:
4.1 利用初等行变换求解逆矩阵:
4.2 利用初等行变换求解方程组的解:
-1. 介绍
注意:矩阵换行与行列式换行不同(行列式的换行值的符号会发生变化)
矩阵的 初等列变换 与 初等行变换 统称为初等变换。
可以通过 初等行变换 转化为 E 的方阵为可逆方阵,否则为奇异矩阵。
初等变换的顺序:
将哪行下面(上面)的数值化为零就将 该行 数乘整数 加到下面(上面)的行上
矩阵初等变换的理解:线性方程组加减消元。

初等变换的三种方式:

0、增广矩阵:
记做: B = (A,b)

1、初等变换的性质:

2、矩阵初等变换的分类:
2.1 普通的行阶梯矩阵:

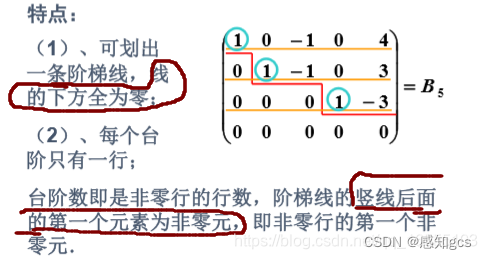
2.2 、行最简形矩阵:




2.3、标准形矩阵:
特性:



3、初等变换的定理:
其中: PA = B 是初等变化的 代数 表达形式。P是某个可逆方阵。

方阵可逆的充要条件:

4、初等变换的应用:
4.1 利用初等行变换求解逆矩阵:
例:求解A 的逆矩阵:
思路:将A 与 E 创建 增广矩阵 B , B= (A,E) >>>>> 通过初等行变换 >>>>>> (E,P) P 就
是A的 可逆矩阵:P * A = E。
4.2 利用初等行变换求解方程组的解:
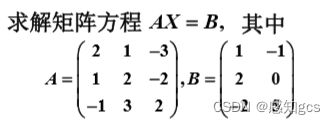
思路:类似上述求解逆矩阵的方法: ![]()

解法:增广矩阵:
相关文章:

七、矩阵的初等变换
目录 -1. 介绍 0、增广矩阵: 1、初等变换的性质: 编辑2、矩阵初等变换的分类: 2.1 普通的行阶梯矩阵: 2.2 、行最简形矩阵: 2.3、标准形矩阵: 3、初等变换的定理: 4、初等变换的应用&…...

CSS background-size
background-size 菜鸟教程 CSS3 background-size 属性 MDN Web 开发技术>CSS:层叠样式表>background-size CSS的background 背景图片自动适应元素大小,实现img的默认效果 background-size:100% 100%; 在CSS中,background-size属性用…...

【机器学习】特征工程之特征选择
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:机器学习 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

Java中PDF文件传输有哪些方法?
专栏集锦,大佬们可以收藏以备不时之需: Spring Cloud 专栏:http://t.csdnimg.cn/WDmJ9 Python 专栏:http://t.csdnimg.cn/hMwPR Redis 专栏:http://t.csdnimg.cn/Qq0Xc TensorFlow 专栏:http://t.csdni…...
前后端分离Vue+ElementUI+nodejs蛋糕甜品商城购物网站95m4l
本文主要介绍了一种基于windows平台实现的蛋糕购物商城网站。该系统为用户找到蛋糕购物商城网站提供了更安全、更高效、更便捷的途径。本系统有二个角色:管理员和用户,要求具备以下功能: (1)用户可以修改个人信息&…...

Pytorch 复习总结 3
Pytorch 复习总结,仅供笔者使用,参考教材: 《动手学深度学习》Stanford University: Practical Machine Learning 本文主要内容为:Pytorch 多层感知机。 本文先介绍了多层感知机的用法,再就训练过程中经常出现的过拟…...

2024年危险化学品经营单位主要负责人证考试题库及危险化学品经营单位主要负责人试题解析
题库来源:安全生产模拟考试一点通公众号小程序 2024年危险化学品经营单位主要负责人证考试题库及危险化学品经营单位主要负责人试题解析是安全生产模拟考试一点通结合(安监局)特种作业人员操作证考试大纲和(质检局)特…...

go使用trpc案例
1.go下载trpc go install trpc.group/trpc-go/trpc-cmdline/trpclatest 有报错的话尝试配置一些代理(选一个) go env -w GOPROXYhttps://goproxy.cn,direct go env -w GOPROXYhttps://goproxy.io,direct go env -w GOPROXYhttps://goproxy.baidu.com/…...
nodejs+vue+ElementUi废品废弃资源回收系统
系统主要是以后台管理员管理为主。管理员需要先登录系统然后才可以使用本系统,管理员可以对系统用户管理、用户信息管理、回收站点管理、站点分类管理、站点分类管理、留言板管理、系统管理进行添加、查询、修改、删除,以保障废弃资源回收系统系统的正常…...

【Java程序设计】【C00277】基于Springboot的招生管理系统(有论文)
基于Springboot的招生管理系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的招生管理系统 本系统分为系统功能模块、管理员功能模块以及学生功能模块。 系统功能模块:在系统首页可以查看首页、专业…...

汇编语言与接口技术实践——秒表
1. 设计要求 基于 51 开发板,利用键盘作为按键输入,将数码管作为显示输出,实现电子秒表。 功能要求: (1)计时精度达到百分之一秒; (2)能按键记录下5次时间并通过按键回看 (3)设置时间,实现倒计时,时间到,数码管闪烁 10 次,并激发蜂鸣器,可通过按键解除。 2. 设计思…...

【数据结构与算法】(19)高级数据结构与算法设计之 图 拓扑排序 最短路径 最小生成树 不相交集合(并查集合)代码示例
目录 6) 拓扑排序KahnDFS 7) 最短路径DijkstraBellman-FordFloyd-Warshall 8) 最小生成树PrimKruskal 9) 不相交集合(并查集合)基础路径压缩Union By Size 图-相关题目 6) 拓扑排序 #mermaid-svg-MQhLsXiMwnlUL3q4 {font-family:"trebuchet ms"…...

OSCP靶场--Nickel
OSCP靶场–Nickel 考点(1.POST方法请求信息 2.ftp,ssh密码复用 3.pdf文件密码爆破) 1.nmap扫描 ┌──(root㉿kali)-[~/Desktop] └─# nmap 192.168.237.99 -sV -sC -p- --min-rate 5000 Starting Nmap 7.92 ( https://nmap.org ) at 2024-02-22 04:06 EST Nm…...

新建工程——库函数版
新建工程——库函数版 s t e p I : 新建工程文件夹 \bf{stepI:新建工程文件夹} stepI:新建工程文件夹 s t e p I I : K e i l 5 新建工程 \bf{stepII:Keil5新建工程} stepII:Keil5新建工程 s t e p I I I : 最终得到工程文件 \bf{stepIII:最终得到工程文件} stepIII:最终得到工…...
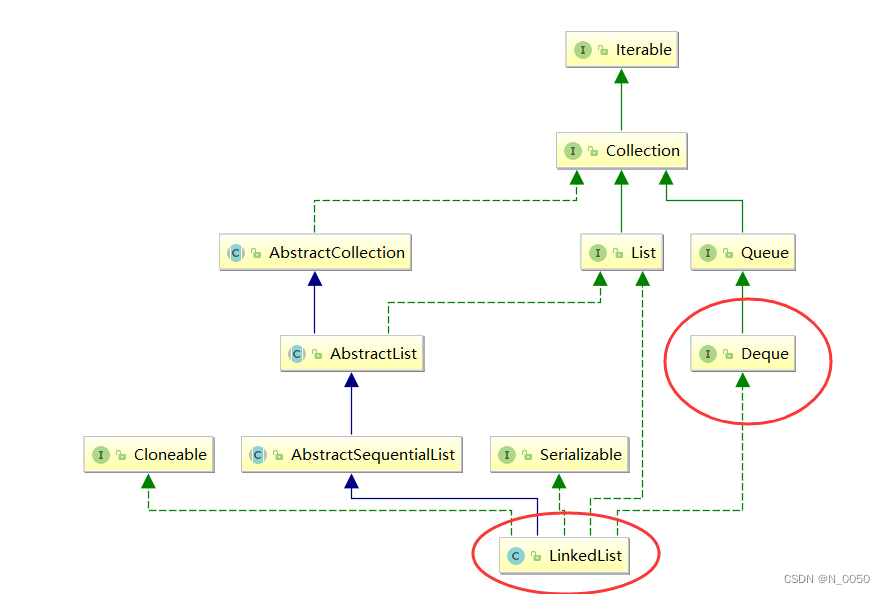
java 数据结构栈和队列
目录 栈(Stack) 栈的使用 栈的模拟实现 栈的应用场景 队列(Queue) 队列的使用 队列模拟实现 循环队列 双端队列 用队列实现栈 用栈实现队列 栈(Stack) 什么是栈? 栈 :一种特殊的线性表,其 只允许在固定的一端进行插入和删除元素操…...

#LLM入门|Prompt#1.8_聊天机器人_Chatbot
聊天机器人设计 以会话形式进行交互,接受一系列消息作为输入,并返回模型生成的消息作为输出。原本设计用于简便多轮对话,但同样适用于单轮任务。 设计思路 个性化特性:通过定制模型的训练数据和参数,使机器人拥有特…...
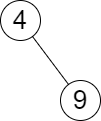
LeetCode 2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
【LetMeFly】2476.二叉搜索树最近节点查询:中序遍历 二分查找 力扣题目链接:https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/ 给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 qu…...

选座位 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 疫情期间,需要大家保证一定的社交距离,公司组织开交流会议,座位有一排共N个座位,编号分别为[0…N-1],要…...
【微服务】mybatis typehandler使用详解
目录 一、前言 二、TypeHandler简介 2.1 什么是TypeHandler 2.1.1 TypeHandler特点 2.2 TypeHandler原理 2.3 mybatis自带的TypeHandler 三、环境准备 3.1 准备一张数据表 3.2 搭建一个springboot工程 3.2.1 基础依赖如下 3.2.2 核心配置文件 3.2.3 测试接口 四、T…...

计网 - 深入理解HTTPS:加密技术的背后
文章目录 Pre发展历史Http VS HttpsHTTPS 解决了 HTTP 的哪些问题HTTPS是如何解决上述三个风险的混合加密摘要算法 数字签名数字证书 Pre PKI - 数字签名与数字证书 PKI - 借助Nginx 实现Https 服务端单向认证、服务端客户端双向认证 发展历史 HTTP(超文本传输协…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
