C语言每日一题(61)盛最多水的容器
题目链接
力扣 11 盛最多水的容器
题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
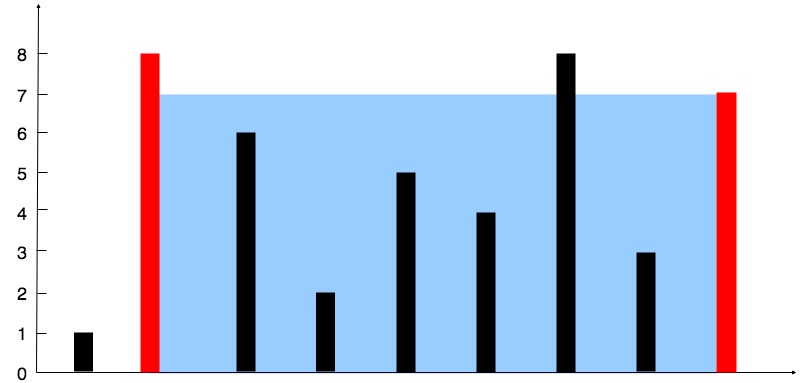
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
思路分析
知识点:双指针
解析:
典型的双指针题,先说做法:
定义左右两个指针分别向数组中间走,可以看出,容器的容量就是两个指针指向的值中最小的那个值乘以两个指针之间的距离,可以用木桶效应来解释,即桶的容量取决于最短的那块木板。
第一次结果出来后,值较小的指针往中间走,这期间更新最大值,直到俩指针相遇。
int maxArea(int* height, int heightSize) {int left=0,right=heightSize-1;int ans=0;while(left<right){int area=fmin(height[left],height[right])*(right-left);ans=fmax(area,ans);if(height[left]<height[right]){left++;}else{right--;}}return ans;}拓展:
为什么不移动最大值而是移动最小值?
可以看看力扣官方的题解,下面是我根据题解总结出来的:
关于无论怎样移动右指针,左指针都不会成为容器的边界(左指针最小)了这句话,我有点稀里糊涂,我的理解可能就在于左指针的值对于容器容量不起决定性作用了,因为无论右指针大还是小,移动后的容量肯定比之前的少(题解有证明),万一一开始的容量不是最大该怎么办?所以只能移动右指针
相关文章:

C语言每日一题(61)盛最多水的容器
题目链接 力扣 11 盛最多水的容器 题目描述 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水…...

uni-app 经验分享,从入门到离职(四)——页面栈以及页面跳转的 API(开发经验总结)
文章目录 📋前言⏬关于专栏 🎯什么是页面栈🧩页面跳转方法📌 uni.navigateTo(OBJECT)📌 uni.redirectTo(OBJECT)📌 uni.reLaunch(OBJECT)📌 uni.switchTab(OBJECT)📌 uni.navigateBa…...

Go Module常用命令
Go Module常用命令TOC Go Module常用命令 go mod init #初始化go.mod go mod tidy #更新依赖文件 go mod download #下载依赖文件 go mod vendor #将依赖转移至本地的vendor文件 go mod edit #手…...

ubuntu压缩和解压
-c 创建 -x 解压 -v 显示过程 -f 文件名 xz格式 tar -tf arm-linux-gnueabi-5.4.0.tar.xz 查看压缩包的内容 tar -xf arm-linux-gnueabi-5.4.0.tar.xz -C / 解压 gz格式 t…...

华为HCIP Datacom H12-831 卷24
多选题 1、如图所示,某园区部署OSPF实现网络互通,其中Area1部署为NSSA区域。某工程师为了实现R1访问R4的环回口地址,在R4的OSPF进程中引入直连路由。以下关于该场景的描述,错误的有哪些项? A、在R4引入直连路由后,R1通过转换后的…...

react + Typescript 中 react有多少内置的类型 分别是什么
react Typescript 中 react有多少内置的类型 分别是什么 React 和 TypeScript 结合使用时,React 提供了一系列的内置类型(也称为类型定义或类型别名)来帮助你在 TypeScript 中编写类型安全的代码。这些类型定义涵盖了 React 的各个方面&…...
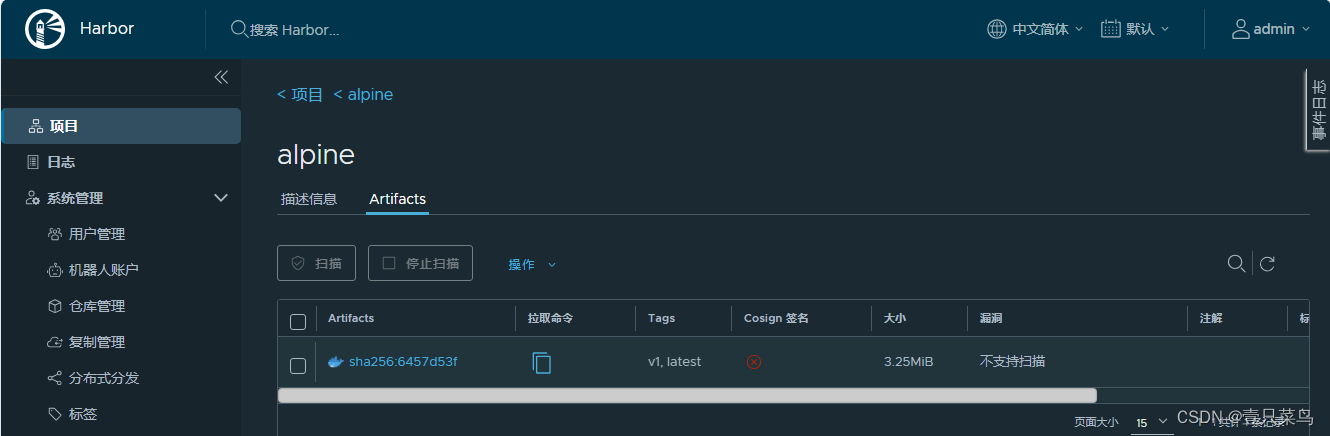
harbor(docker仓库)仓库部署 - 高可用
harbor(docker仓库)仓库部署 - 高可用 1. harbor高可用1.1 方案说明1. 双主复制2. 多harbor实例共享后端存储 1.2 部署高可用(多harbor实例共享后端存储)1. 服务器划分2. 安装harbor(先部署一套Harbor,用于…...

题目 1262: 邮局选址问题
题目描述: 在一个按照东西和南北方向划分成规整街区的城市里,n个居民点散乱地分布在不同的街区中。用x 坐标表示东西向,用y坐标表示南北向。各居民点的位置可以由坐标(x,y)表示。街区中任意2 点(x1,y1)和(x2,y2)之间的距离可以用数值|x1-x2||y1-y2|度量…...

内核内存回收关键隐藏变量之page引用计数
在分析内核内存回收源码时,page引用计数并不显眼,但是page引用计数对page的内存回收至关重要。本文基于linux-4.18.0-240版本内核源码,总结下文件页page的引用计数的相关细节。首先是get_page()和put_page()函数,分别令page引用计…...

数据结构---链表的基本操作
头插法遍历链表尾插法头删法尾删法按位置插入数据按位置删除数据直接插入排序 链表翻转快慢指针 linklist.c #include <stdio.h> #include <stdlib.h> #include "./linklist.h"linklist* create_linklist(void) {linklist* head (linklist*)malloc(siz…...

异步框架Celery在Django中的运用
参考博客:https://www.cnblogs.com/pyedu/p/12461819.html 参考视频:01 celery的工作机制_哔哩哔哩_bilibili 定义:简单灵活、处理大量消息的分布式系统,专注于实时处理异步队列,支持任务调度 主要架构: …...
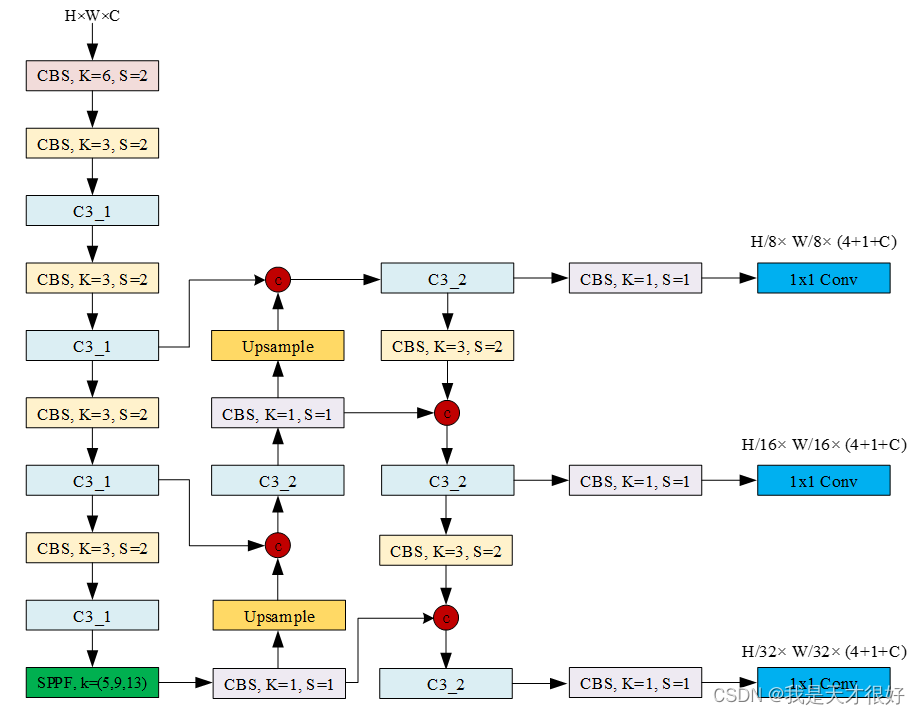
YOLOv5代码解读[02] models/yolov5l.yaml文件解析
文章目录 YOLOv5代码解读[02] models/yolov5l.yaml文件解析yolov5l.yaml文件检测头1--->耦合头检测头2--->解耦头检测头3--->ASFF检测头Model类解析parse_model函数 YOLOv5代码解读[02] models/yolov5l.yaml文件解析 yolov5l.yaml文件 # YOLOv5 🚀 by Ult…...

智能搬运机器人|海格里斯将如何持续推进工业和物流的智能化升级与发展?
存取、搬运、分拣是物流行业中的通用功能,但具体到每个行业又十分不同,例如:新能源电池领域,它所搬运的东西是电池,50KG~200KG;快递行业领域,所要处理的物料是那种扁平件和信封等等,…...
linux之前后端项目部署与发布
目录 前言 简介 一、安装Nginx 二、后端部署 2.1多个tomcat负载均衡 2.2 负载均衡 2.3 后端项目部署 三、前端部署 1.解压前端 2.Nginx配置文件修改 3.IP域名映射 4.重启Nginx服务 前言 上篇博主已经讲解过了单机项目的部署linux之JAVA环境配置JDK&Tomcat&a…...

Python 高级语法:一切皆对象
1 “一切皆对象”是一种核心设计哲学 在编程领域,特别是面向对象编程(OOP)中,“一切皆对象”是一种核心设计哲学。这种哲学主张,无论是数据、函数、还是更复杂的结构,都可以被视为对象,并赋予…...
python jupyter notebook打开页面方便使用
如果没安装jupyter, 请安装: pip install jupyter notebook 运行jupyter notebook jupyter-notebook...
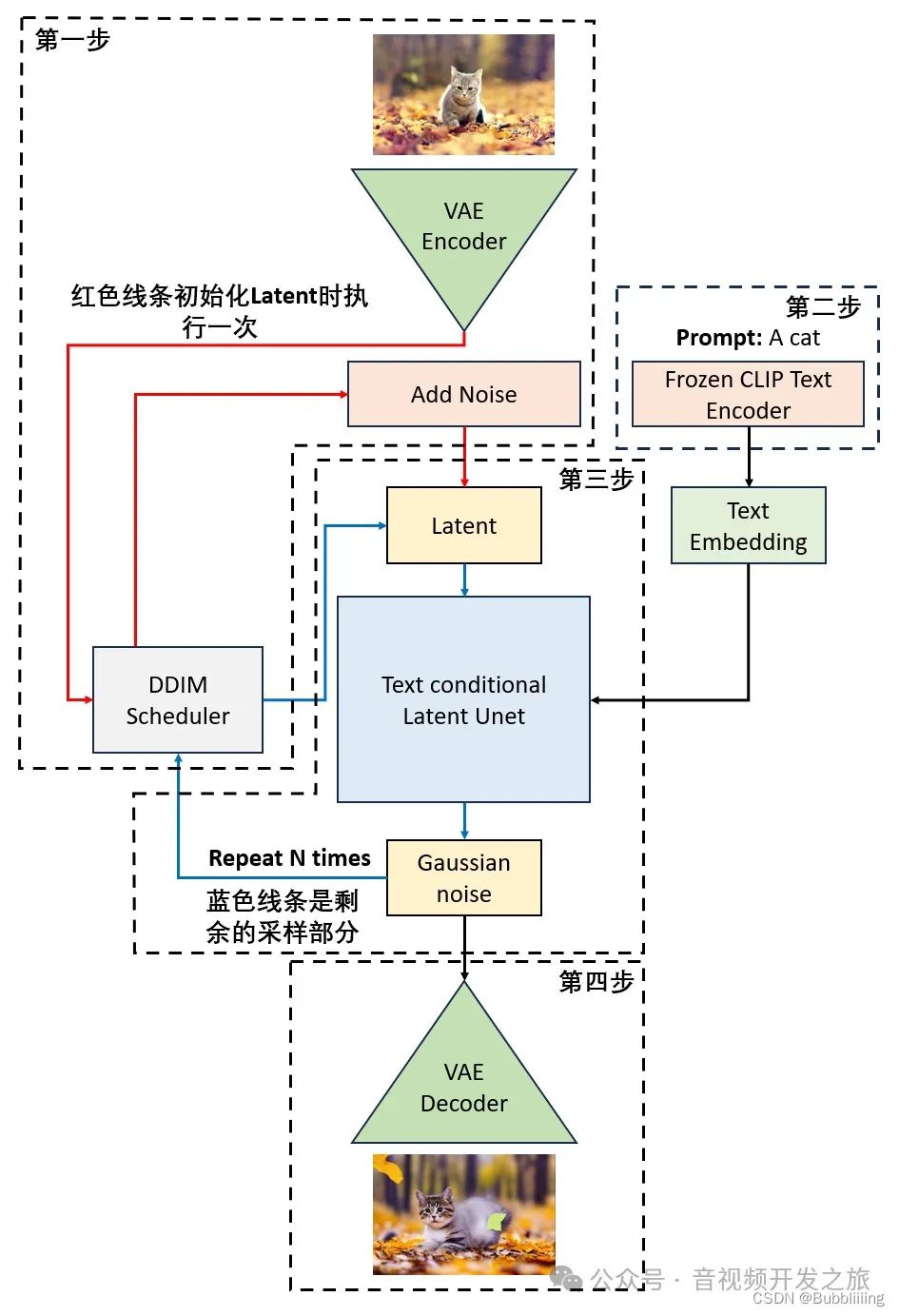
音视频开发之旅(69)-SD图生图
目录 1. 效果展示 2. ControlNet介绍 3. 图生图流程浅析 4. SDWebui图生图代码流程 5. 参考资料 一、效果展示 图生图的应用场景非常多,比较典型的应用场景有风格转化(真人与二次元)、线稿上色、换装和对图片进行扩图等,下面…...
)
數據集成平台:datax將hive數據步到mysql(全部列和指定列)
數據集成平台:datax將hive數據步到mysql(全部列和指定列) 1.py腳本 傳入參數: target_database:數據庫 target_table:表 target_columns:列 target_positions:hive列的下標&#x…...
pikachu靶场-File Inclusion
介绍: File Inclusion(文件包含漏洞)概述 文件包含,是一个功能。在各种开发语言中都提供了内置的文件包含函数,其可以使开发人员在一个代码文件中直接包含(引入)另外一个代码文件。 比如 在PHP中,提供了&…...

[今天跟AI聊聊职场] ~你能接受你的直接领导能力不如你,年纪还比你小很多吗?
知乎问题: 弟弟今年35岁,刚换了一份工作,直接领导小A比他小5岁,各方面经验没有他成熟。难的工作都是弟弟在做,功劳都被直接领导小A抢走了,有时候还要被直接领导小A打压。弟弟感觉升职加薪无望。现在找工作不…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
