Educational Codeforces Round 160 (Rated for Div. 2) E. Matrix Problem(费用流)
原题链接:E. Matrix Problem
题目大意:
给出一个 n n n 行 m m m 列的 0 / 1 0/1 0/1 矩阵,再给出一些限制条件:一个长为 n n n 的数组 a a a,和一个长为 m m m 的数组 b b b 。
其中 a i a_{i} ai 表示第 i i i 行要有 恰好 a i a_{i} ai 个 1 1 1 , b j b_{j} bj 表示第 j j j 列要有 恰好 b j b_{j} bj 个 1 1 1 ,保证 1 ≤ a i ≤ m , 1 ≤ b j ≤ n 1 \leq a_{i} \leq m,1 \leq b_{j} \leq n 1≤ai≤m,1≤bj≤n 。
你可以使用 任意多次 操作,将一个 0 0 0 翻转成 1 1 1 ,或将 1 1 1 翻转成 0 0 0 。
问最少的操作次数是多少,才能使得这个矩阵满足以上 a , b a,b a,b 限制,如果怎么操作都不能满足以上限制则输出 − 1 -1 −1 。
解题思路:
套路的,我们将行和列看成点,行为左部,列为右部,而每个位置 ( i , j ) (i,j) (i,j) 的信息看成是一条 i i i 和 j j j 的边,这样我们的矩阵就会形成一张天然的二分图。
回到这一题,首先要是连 ∑ i = 1 n a i ≠ ∑ i = 1 m b i \sum_{i=1}^{n} a_{i} \neq \sum_{i=1}^{m} b_{i} ∑i=1nai=∑i=1mbi 了,那肯定无论如何都不会满足的,但只有这个条件是不够的,而且很容易找出反例,但我们可以先判掉,使得接下来 ∑ i = 1 n a i = ∑ i = 1 m b i \sum_{i=1}^{n} a_{i} = \sum_{i=1}^{m} b_{i} ∑i=1nai=∑i=1mbi ,方便后续讨论。
考虑全是 0 0 0 我们怎么做,本质上就是每条边流量为 1 1 1 ,源点 S → [ 1 , 2 , . . . , n ] S \rightarrow [1,2,...,n] S→[1,2,...,n] 连一条流量为 a i a_{i} ai 的边, [ 1 , 2 , . . . , m ] → [1,2,...,m] \rightarrow [1,2,...,m]→ 汇点 T T T 连一条流量为 b i b_{i} bi 的边,然后跑一个最大流即可。
当我们发现最大流和 ∑ i = 1 n a i \sum_{i=1}^{n} a_{i} ∑i=1nai 不等,那么显然无论如何操作也是不行的。
(其实本质上就是在做一个匹配的操作:点 A A A 可以匹配 a i a_{i} ai 个人,点 B B B 可以匹配 b i b_{i} bi 个人,看是否使得每个人都能匹配完全)
但是这一题是带操作次数的条件的,我们要最小操作次数,而且矩阵初始值也不是全为 0 0 0 ,这要怎么办?
首先考虑 0 0 0 的位置的影响,如果某个地方的 0 0 0 无论如何都要翻转为 1 1 1 的,那么这个 0 0 0 对操作的贡献是固定为 1 1 1 的,我们直接操作就好。而其他无所谓的 0 0 0 显然去操作只会让操作数变多,不优。
再考虑 1 1 1 的位置的影响,无论如何我们都要把多余的 1 1 1 给删掉,我们不妨先全部删除了,操作数就是 1 1 1 的个数。再考虑哪些 1 1 1 是可以作为选择的,然后反悔我们的删除操作,把这个 1 1 1 加回来即可,这样对我们操作的贡献是为 − 1 -1 −1 的。
按照上面的转化,假设矩阵为 g n , m g_{n,m} gn,m 那么:
- 先假设矩阵全为 0 0 0 ,统计 1 1 1 的个数。
- 当 g i , j = 1 g_{i,j}=1 gi,j=1 时,我们添加边 i → j i \rightarrow j i→j ,流量为 1 1 1,费用为 − 1 -1 −1 (反悔)。
- 当 g i , j = 0 g_{i,j}=0 gi,j=0 时,我们添加边 i → j i \rightarrow j i→j ,流量为 1 1 1,费用为 1 1 1 (固定)。
- S S S 向 i i i 连上流量为 a i a_{i} ai,费用为 0 0 0 的边, j j j 向 T T T 连上流量为 b j b_{j} bj,费用为 0 0 0 的边。
- 这里的 i , j i,j i,j 分别指的是 左部 的点的编号和 右部 的点的编号。
如果最大流不为 ∑ i = 1 n a i \sum_{i=1}^{n} a_{i} ∑i=1nai 说明不能匹配完全,输出 − 1 -1 −1 。
否则我们所需要的最小操作次数就是 ∑ i = 1 n ∑ j = 1 m g i , j + \sum_{i=1}^{n}\sum_{j=1}^{m}g_{i,j}+ ∑i=1n∑j=1mgi,j+ 最小费用 (固定 + + + 反悔的和)。
代码使用的是 S p f a + D i n i c Spfa+Dinic Spfa+Dinic 的费用流。
时间复杂度: O ( n 3 m 3 ) O(n^{3}m^{3}) O(n3m3) (伪多项式复杂度,可以通过)
AC代码:
#include <bits/stdc++.h>
using namespace std;using PII = pair<int, int>;
using i64 = long long;template<class Ty>
struct MCmaxFlow {const Ty INF = numeric_limits<Ty>::max();int S, T, n; Ty MF = 0, MC = 0;struct Edge {int v, nxt; Ty f, w;Edge() : Edge(0, 0, 0, 0) {};Edge(int v, int nxt, Ty f, Ty w) : v(v), nxt(nxt), f(f), w(w) {};};vector<Ty> dist;vector<int> cur, h;vector<bool> vis;vector<Edge> E;MCmaxFlow(int _) : n(_) { init(_); };void init(int _) {dist.resize(_ + 1);vis.resize(_ + 1);cur.resize(_ + 1);h.resize(_ + 1);E.resize(2);}void add(int u, int v, Ty f, Ty w) {E.emplace_back(v, h[u], f, w), h[u] = int(E.size()) - 1;}void addEdge(int u, int v, Ty f, Ty w) {add(u, v, f, w), add(v, u, 0, -w);}bool SPFA() {dist.assign(n + 1, INF);queue<int> que;dist[S] = 0, cur[S] = h[S];que.push(S);while (que.size()) {int u = que.front(); que.pop();vis[u] = false;for (int i = h[u]; i; i = E[i].nxt) {auto& [v, nxt, f, w] = E[i];if (f && dist[v] > dist[u] + w) {dist[v] = dist[u] + w;if (!vis[v]) {vis[v] = true;cur[v] = h[v];que.push(v);}}}}return dist[T] != INF;}Ty DFS(int u, Ty flow) {if (u == T) return flow;Ty last = flow;vis[u] = true;for (int i = cur[u]; i && last; i = E[i].nxt) {cur[u] = i;auto& [v, nxt, f, w] = E[i];if (f && !vis[v] && dist[v] == dist[u] + w) {Ty cost = DFS(v, min(f, last));if (!cost) dist[v] = INF;E[i].f -= cost, E[i ^ 1].f += cost;last -= cost;}}vis[u] = false;return flow - last;}void work() {while (SPFA()) {Ty flow = DFS(S, INF);MC += dist[T] * flow;MF += flow;}}
};void solve() {int n, m;cin >> n >> m;MCmaxFlow<int> G(n + m + 2);vector g(n + 1, vector<int>(m + 1));int ans = 0;// i -> j 连边for (int i = 1; i <= n; ++i) {for (int j = 1; j <= m; ++j) {cin >> g[i][j];if (g[i][j]) {G.addEdge(i, n + j, 1, -1);++ans;} else {G.addEdge(i, n + j, 1, 1);}}}G.S = n + m + 1, G.T = G.S + 1;int suma = 0, sumb = 0;// S -> i 连边for (int i = 1; i <= n; ++i) {int x; cin >> x;G.addEdge(G.S, i, x, 0);suma += x;}// j -> T 连边for (int i = 1; i <= m; ++i) {int x; cin >> x;G.addEdge(n + i, G.T, x, 0);sumb += x;}//先特判 sum a != sum bif (suma != sumb) {cout << -1 << '\n';return;}G.work();//再特判 maxFlow != sum aif (G.MF != suma) {cout << -1 << '\n';return;}//答案就是 sum g[i][j] + minCostcout << ans + G.MC << '\n';
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1; //cin >> t;while (t--) solve();return 0;
}
相关文章:
 E. Matrix Problem(费用流))
Educational Codeforces Round 160 (Rated for Div. 2) E. Matrix Problem(费用流)
原题链接:E. Matrix Problem 题目大意: 给出一个 n n n 行 m m m 列的 0 / 1 0/1 0/1 矩阵,再给出一些限制条件:一个长为 n n n 的数组 a a a,和一个长为 m m m 的数组 b b b 。 其中 a i a_{i} ai 表示第 …...
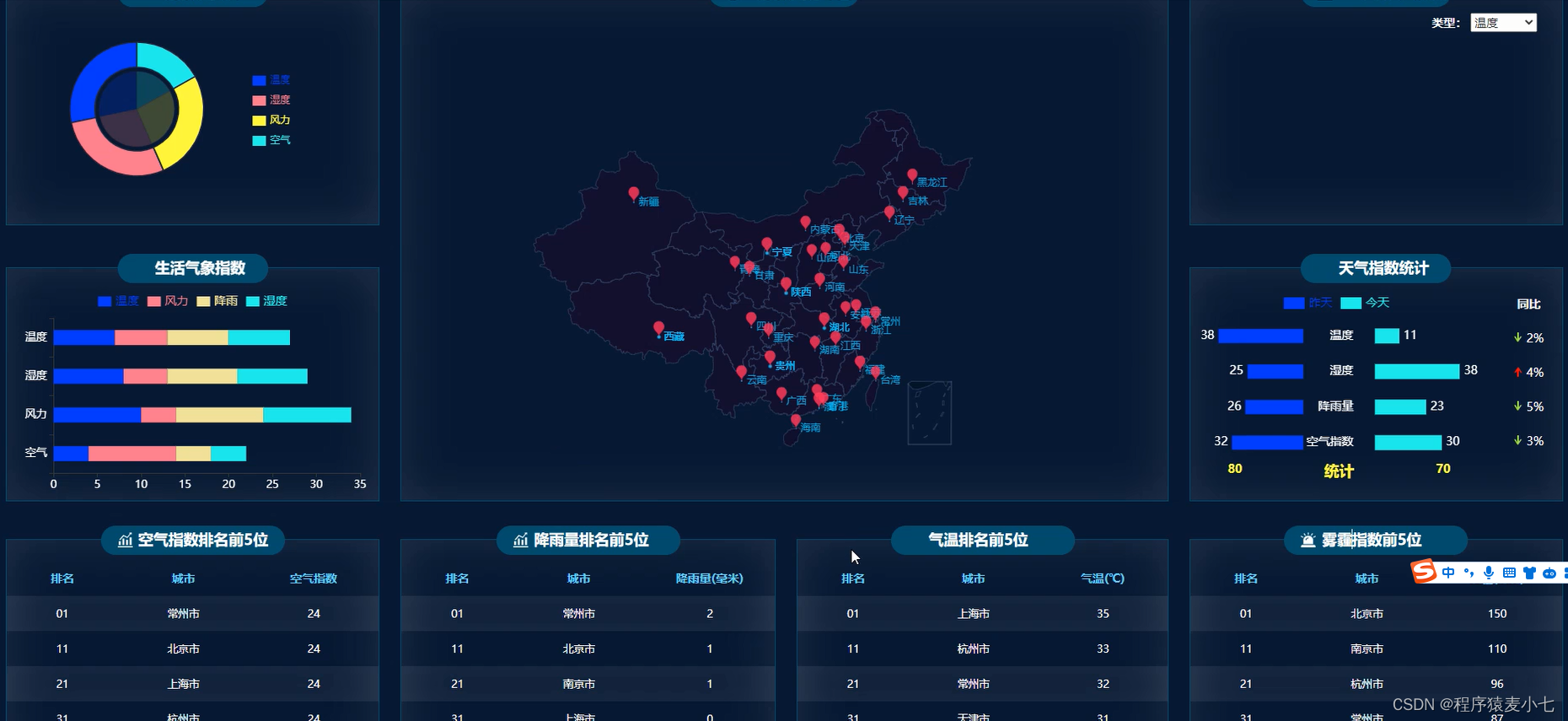
基于SpringBoot的气象数据监测分析大屏
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...

关于硅的制造芯片的过程
芯片是如何制作的? 先将硅融化制成硅晶片,再用光刻机印压电路。 bilibili芯片制作视频 硅晶片作为现代芯片的主要元件,广泛用于集成电路。 首先将多晶硅放入特制的密封炉,排除其中空气后加热到1420摄氏度,将融化的硅放…...

【深度学习笔记】3_10 多层感知机的PyTorch实现
注:本文为《动手学深度学习》开源内容,仅为个人学习记录,无抄袭搬运意图 3.10 多层感知机的简洁实现 下面我们使用PyTorch来实现上一节中的多层感知机。首先导入所需的包或模块。 import torch from torch import nn from torch.nn import …...

输入法在 Android13上候选词 候选区域 不显示的问题
背景 自研的输入法发现在 Android13 平台上不显示候选区域,在之前平台上以及需求是输入英文时不显示,中文需要显示。 最终解决办法:setExtractViewShown(false) Override public View onCreateCandidatesView() {...setExtractViewShown(f…...

Java 面向对象进阶 18 JDK8、9开始新增的方法;接口的应用;适配器设计模式;内部类(黑马)
一、JDK8开始新增的方法 默认方法不是抽象方法,所以不强制被重写: 但是如果被重写,就要去掉default关键字: public可以省略,但是default不可以省略: public是灰色的,代表可以省略 但是default是…...
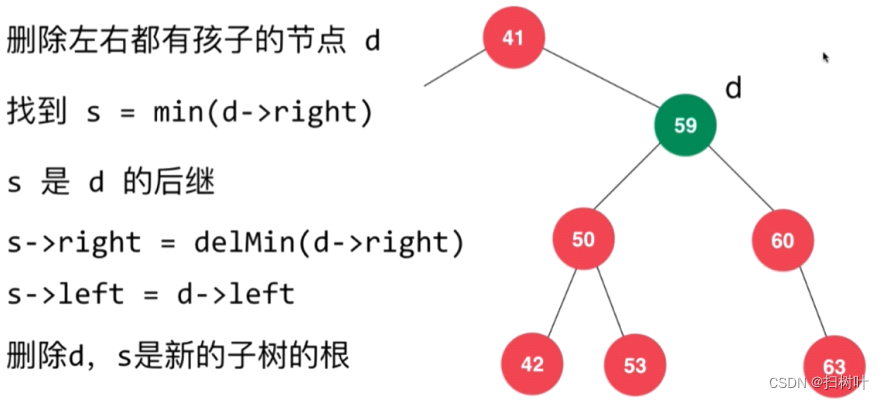
数据结构-二分搜索树(Binary Search Tree)
一,简单了解二分搜索树 树结构: 问题:为什么要创造这种数据结构 1,树结构本身是一种天然的组织结构,就好像我们的文件夹一样,一层一层的. 2,树结构可以更高效的处理问题 二,二分搜索树的基础 1、二叉树 2,二叉树的重要特性 满二叉树 总结: 1. 叶子结点出现在二叉树的最…...

YOLO如何训练自己的模型
目录 步骤 一、打标签 二、数据集 三、跑train代码出模型 四、跑detect代码出结果 五、详细操作 步骤 一、打标签 (1)在终端 pip install labelimg (2)在终端输入labelimg打开 如何打标签: 推荐文章…...
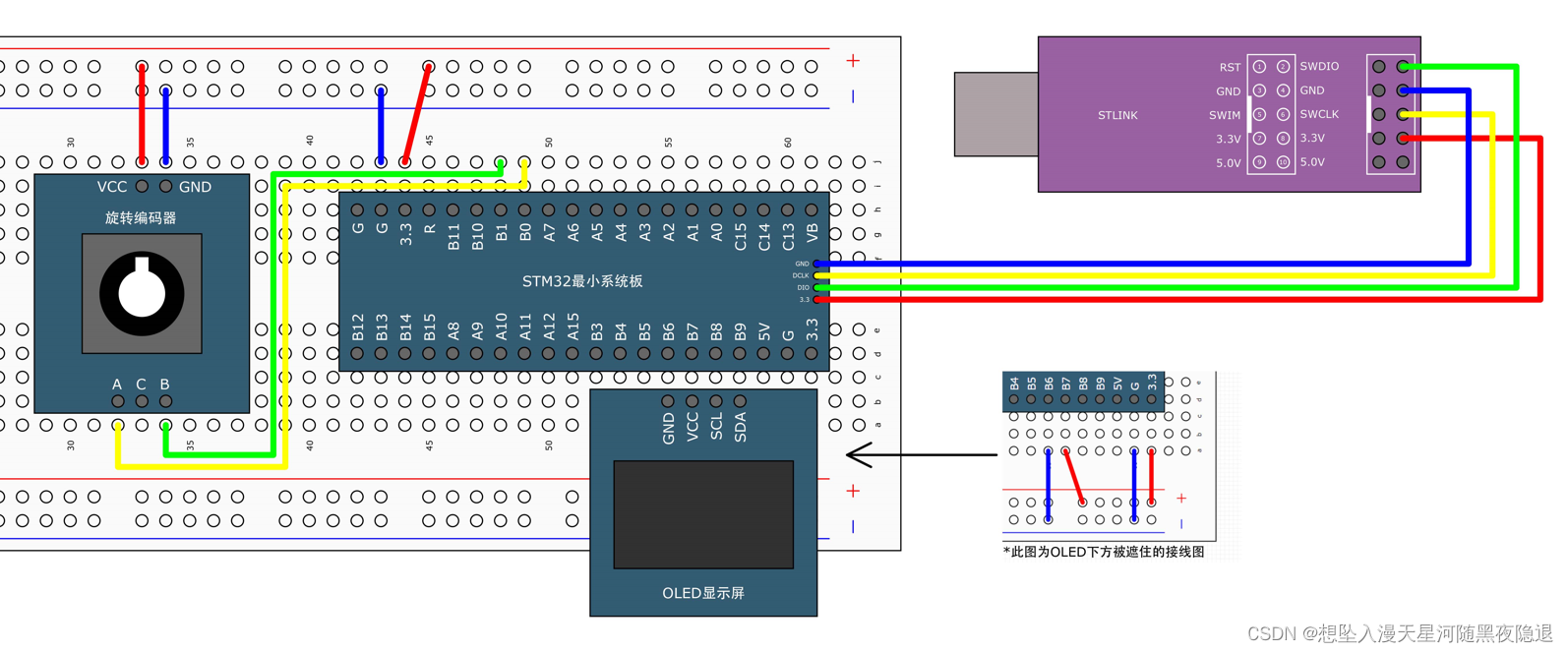
05 EXTI外部中断
一、中断系统 中断系统:管理和执行中断的逻辑结构。中断:在主程序运行过程中,出现了特定的中断触发条件——中断源,使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继…...

2024.2.23
1.1.1 信号默认、捕获、忽略处理(普通信号) #include <myhead.h> void handler(int signo) {if(signoSIGINT){printf("用户键入 ctrlc\n");} } int main(int argc, const char *argv[]) {//忽略信号if(signal(SIGINT,SIG_IGN)SIG_ERR){perror("signal er…...

PHP实现分离金额和其他内容便于统计计算
得到的结果可以粘贴到excel计算 <?php if($_GET["x"] "cha"){ $tips isset($_POST[tips]) ? $_POST[tips] : ; $pattern /(\d\.\d|\d)/; $result preg_replace($pattern, "\t\${1}\t", $tips); echo "<h2><strong>数…...

基础数据结构和算法《》
递归 1.递归应该一种比较常见的实现一些特殊代码逻辑时需要做的,但常常也是最绕的一种方式,在解释递归 之前,我们用循环和递归来做个比较1.1.如果你打开一扇门后,同样发现前方也有一扇们,紧接着你又打开下一扇门...直…...
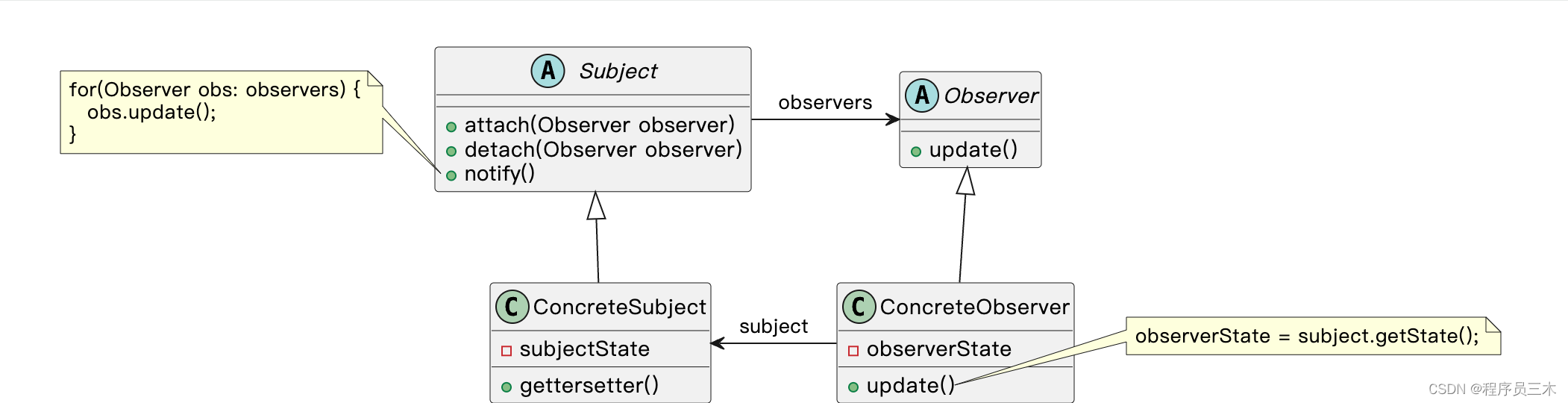
[设计模式Java实现附plantuml源码~行为型]对象间的联动~观察者模式
前言: 为什么之前写过Golang 版的设计模式,还在重新写Java 版? 答:因为对于我而言,当然也希望对正在学习的大伙有帮助。Java作为一门纯面向对象的语言,更适合用于学习设计模式。 为什么类图要附上uml 因为很…...
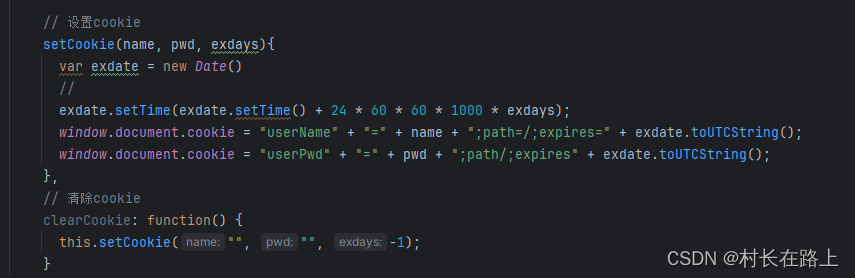
vue3+js 实现记住密码功能
常见的几种实现方式 1 基于spring security 的remember me 功能 localStorage 除非主动清除localStorage 里的信息 ,不然永远存在,关闭浏览器之后下次启动仍然存在 存放数据大小一般为5M 不与服务器进行交互通信 cookies 可以…...

基于单片机的太阳能电池板自动跟踪系统的研究
摘要 伴随着人类社会的发展,人口基数越来越大,电量消耗巨大,传统发电原 料污染环境的同时,可用量日益减少,给人类未来生产生活带来了一定的威胁, 因而解决日益剧增的用电量,寻求一种新能源显得极其重要。论文正是基于此 背景下,针对当前太阳能电池板采光率低、自动化水…...

React 模态框的设计(二)
自定义组件是每个前端开发者必备的技能。我们在使用现有框架时难免有一些超乎框架以处的特别的需求,比如关于弹窗,每个应用都会用到,但是有时我们使用的框架中提供的弹窗功能也是功能有限,无法满足我们的应用需求,今天…...

操作符详解3
✨✨ 欢迎大家来到莉莉的博文✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 前面我们已经讲过算术操作符、赋值操作符、逻辑操作符、条件操作符和部分的单目操作 符,今天继续介绍一部分。 目录 1.操作符的分类 2…...

【C语言基础】:操作符详解(一)
文章目录 操作符详解1. 操作符的分类2. 二进制和进制转换2.1 什么是二进制、八进制、十进制、十六进制2.1.1 二进制和进制转换2.1.2 二进制转十进制2.2.3 二进制转八进制2.2.4 二进制转十六进制 3. 源码、反码、补码4. 移位操作符4.1 左移操作符4.2 右移操作符 5. 位操作符&…...
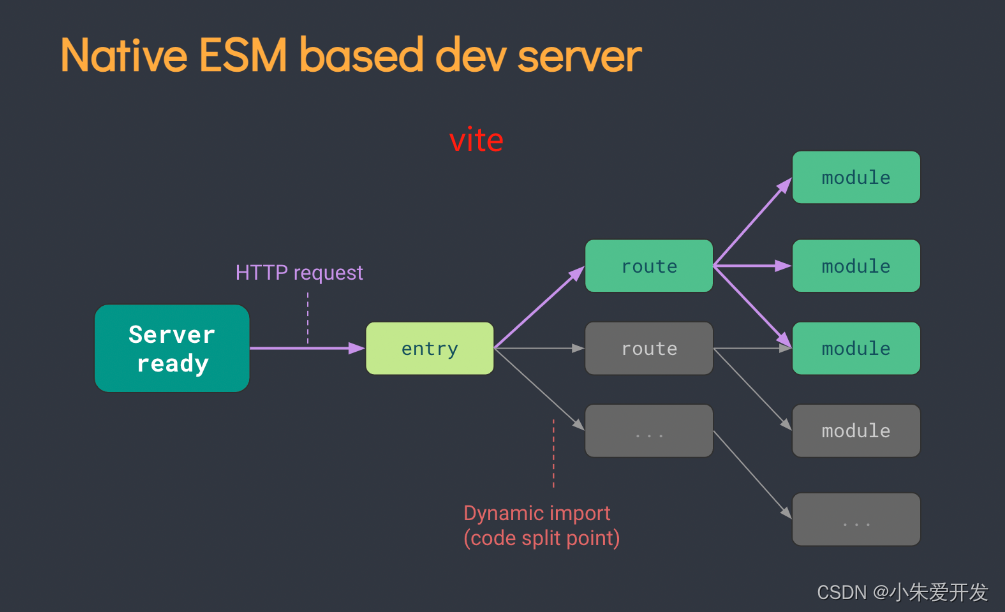
通俗易懂分析:Vite和Webpack的区别
1、对项目构建的理解 先从浏览器出发, 浏览器是由浏览器内核和JS引擎组成;浏览器内核编译解析html代码和css代码,js引擎编译解析JavaScript代码;所以从本质上,浏览器只能识别运行JavaScript、CSS、HTML代码。 而我们在…...

OpenCart程序结构与业务逻辑
一、程序业务逻辑说明 在 OpenCart 中,index.php 文件是整个应用程序的入口文件,它负责初始化应用程序并调度请求。以下是 index.php 文件加载执行的流程: 1. **设置路径常量:** - index.php 首先定义了一些重要的路径常量&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

嵌入式面试常问问题
以下内容面向嵌入式/系统方向的初学者与面试备考者,全面梳理了以下几大板块,并在每个板块末尾列出常见的面试问答思路,帮助你既能夯实基础,又能应对面试挑战。 一、TCP/IP 协议 1.1 TCP/IP 五层模型概述 链路层(Link Layer) 包括网卡驱动、以太网、Wi‑Fi、PPP 等。负责…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...

uni-app学习笔记二十三--交互反馈showToast用法
showToast部分文档位于uniapp官网-->API-->界面:uni.showToast(OBJECT) | uni-app官网 uni.showToast(OBJECT) 用于显示消息提示框 OBJECT参数说明 参数类型必填说明平台差异说明titleString是提示的内容,长度与 icon 取值有关。iconString否图…...

Flask和Django,你怎么选?
Flask 和 Django 是 Python 两大最流行的 Web 框架,但它们的设计哲学、目标和适用场景有显著区别。以下是详细的对比: 核心区别:哲学与定位 Django: 定位: "全栈式" Web 框架。奉行"开箱即用"的理念。 哲学: "包含…...
