随机分布模型
目录
前言
一、离散型随机变量
1.1 0-1分布
1.2 二项分布
1.3 帕斯卡分布
1.4 几何分布
1.5 超几何分布
1.6 泊松分布
二、连续型随机变量
2.1 均匀分布
2.2 指数分布
2.3 高斯分布/正态分布
2.4 分布(抽样分布)
2.5 t分布(抽样分布)
2.6 F分布(抽样分布)
2.7 分布
2.8 瑞利分布
2.9 莱斯分布
2.10 韦布尔分布
2.11 分布
2.12 对数正态分布
2.13 柯西分布
三、性质及定理
3.1、均值性质
3.2、方差性质
3.3、定理
总结
前言
本文首先结合自身研究经验,在前言部分简单叙述自己对随机概念的理解,描述可能不是很专业,仅供参考。正文部分重点描述常见的离散型随机变量以及连续性随机变量的分布类型,这部分参考各方资料,如果问题,欢迎评论区具体指出。
个人认为目前随机概念更多的是对结果的描述,人们往往容易忽略产生这种随机结果的原因。以抛骰子为例,普遍认为,如果随机抛出骰子,每次投出结果是不同的,我们把这种输出结果看似随机的现象认为是随机事件。
事实上,抛骰子可以认为是一种相当复杂的物理过程,其结果受抛出骰子时,手对骰子的力,所处环境中的重力,骰子飞行过程受到的阻力以及骰子碰撞地面的受力情况等诸多因素的影响。我们尝试对抛骰子这样一个物理过程进行精准建模,在抛骰子过程中,如果我们能够弄清楚影响骰子结果的所有要素,并且也能在投骰子过程精确的保证所有要素在每次实验都能一致,是否意味着每次实验结果都能惊人的一致。
问题是对抛骰子过程的建模是非常困难的,一方面整个物理过程影响要素很多,碰撞方面机理或许不是完全清楚,另一方面,很难保证抛骰子的力度以及角度完全确定。因此,目前的研究是将其作为一个黑盒子模型进行研究,模型输入是随机抛出骰子,投出骰子的状态、使出的力度、投出的角度凭借试验者的经验进行,这样就可以对模型输出的结果进行研究,并基于概率统计原理对结果进行分析。
由于结果随机出现的特性,投骰子被运用到赌博上,一些人为了得到想要的结果上,一方面,有些人可能会在大量投骰子训练过程中找到投出特定点数的手感,以此大幅提高投出特定点数的概率;另一方面,有些人会对骰子进行改造,如改变骰子重心(利用重心越低,物理状态越稳定的规律),使其投出特定点数的概率大大提升。
上述论述多是自己的遐想,感兴趣的读者可以以此来对随机概念进行新的思考。有些随机过程并不像投骰子那样可以轻易改变分布类型,如接收机中的热噪声,或者说产生各种随机现象的机理并不容易研究,而我们又急需从随机的结果中获取所需的信息(个人感觉有点像现在的人工智能,机器学习),因此,人们巧妙的避开机理上的问题,用统计结果的分布特点来描述整个过程,利用少数的统计参量依概率描述复杂的模型准确性。为了更加严谨描述随机现象,随机结果用随机变量描述,并根据结果特点分为离散型随机变量和连续性随机变量,下面简单介绍。
一、离散型随机变量
1.1 0-1分布
0-1分布又称两点分布或伯努利( Bernoulli)分布,试验结果只有两个(如成功、失败)。设随机变量X 只取 0或 1两个值,它的分布律为
则称随机变量 X 服从参数为 p的(0 —1)分布,记作。
均值
方差
1.2 二项分布
重复地进行 n 次独立伯努利试验(“重复” 是指这个试验中各次试验条件相同,“独立”是指各次试验的结果互不影响),结果为1的试验次数服从二项分布。设随机变量X 的所有可能值为0, 1, 2,… ,n, 其分布律为
则称随机变量 X 服从参数为 p的(0 —1)分布,记作
均值
方差
1.3 帕斯卡分布
在重复、独立的伯努利试验,设每次试验成功的概率为p,失败的概率为q= 1- p,若将试验进行到出现r(r为常数)次成功为止,以随机变量X表示所需试验次数,则 X是离散型随机变量, 其分布律为为:
则称随机变量 X 服从参数为 p,r的几何分布,记作
均值
方差
1.4 几何分布
重复进行随机事件,直到事件发生为止才停下,X 为首次发生时共做的事件的次数。设随机变量X 的所有可能值为1, 2,… , 其分布律为
则称随机变量 X 服从参数为 p的几何分布,记作
均值
方差
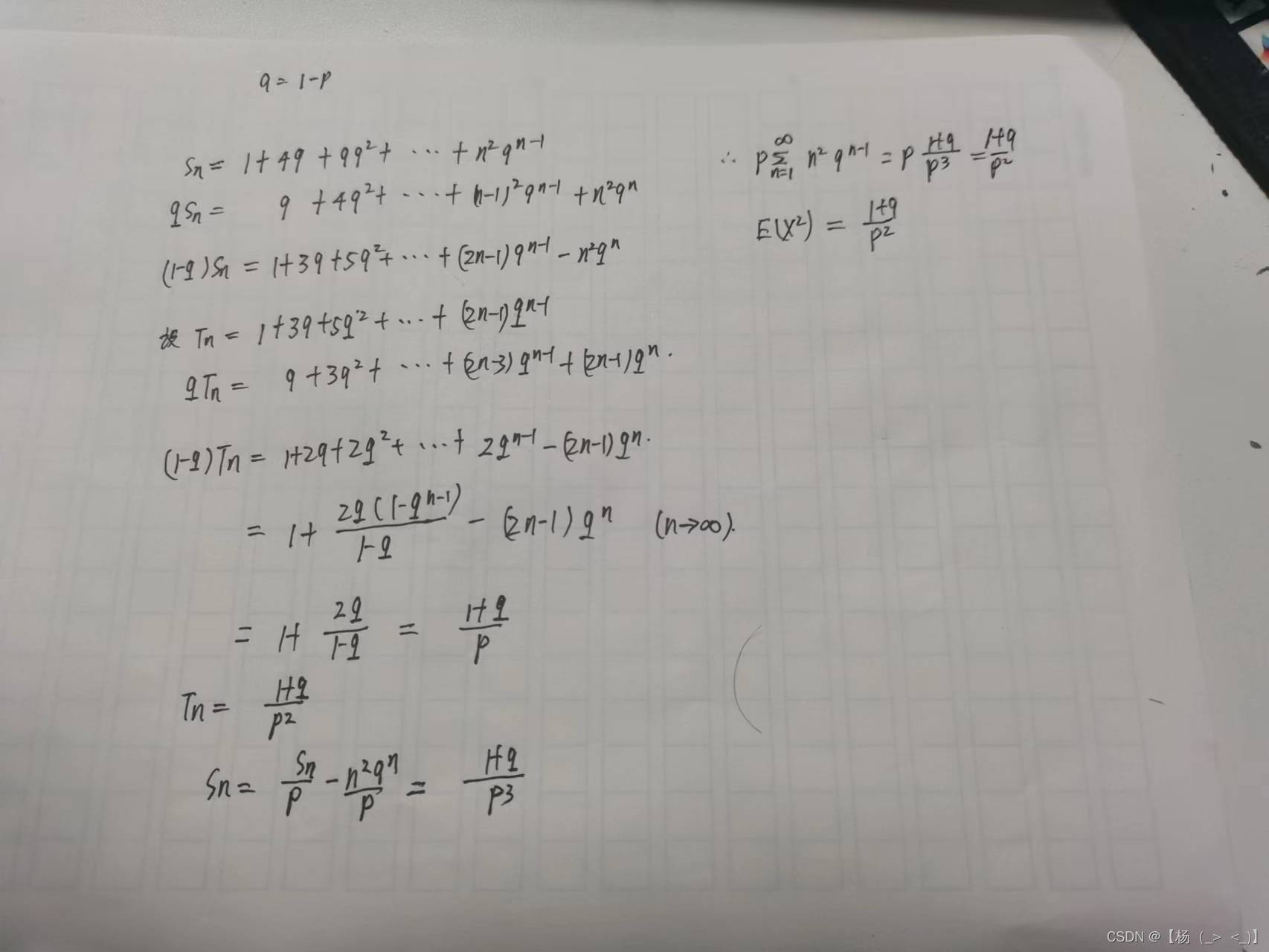
1.5 超几何分布
N 个产品,其中 M 个次品,从中任取 n 个。 X 为这 n 个中的次品数,则 X∼H(n,M,N) 。分布律为:
均值
方差
1.6 泊松分布
设随机变量X 的所有可能值为0, 1, 2,… , 其分布律为
其中是常数,则称X 服从参数为
的泊松分布,记作
均值
方差
二、连续型随机变量
2.1 均匀分布
概率密度函数
均值
方差
2.2 指数分布
概率密度函数
均值
方差
2.3 高斯分布/正态分布
概率密度函数
均值
方差
2.4 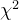 分布(抽样分布)
分布(抽样分布)
设X1, X2, … , Xn是来自总体N(0,1)的样本, 则称统计量:
服从自由度为 n 的分布。概率密度函数
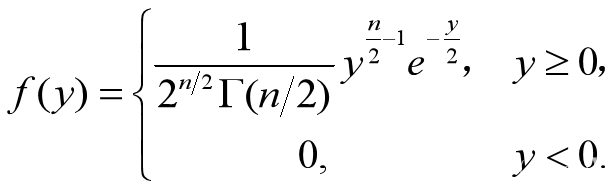
其中伽玛函数
![]()
均值
方差
2.5 t分布(抽样分布)
设X~N(0,1) , Y~ , 且X与Y相互独立,则称随机变量
服从自由度为 n的 t 分布.t 分布又称学生氏(student)分布.概率密度函数

均值
方差
2.6 F分布(抽样分布)
设与
,U与V相互独立,则称随机变量
服从自由度为n1及 n2 的F分布,n1称为第一自由度,n2称为第二自由度。概率密度为
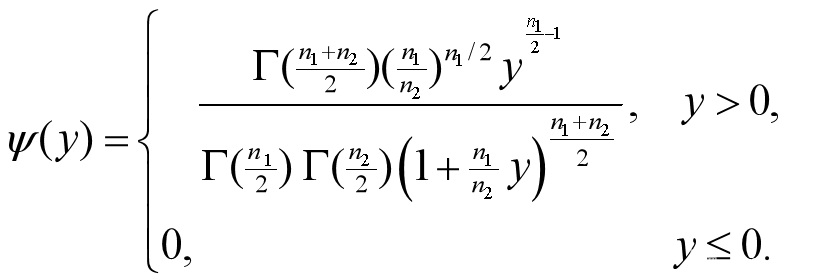
均值
方差
2.7 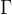 分布
分布
假设随机变量X为等到第α件事发生所需之等候时间,且每个事件之间的等待时间是互相独立的,α为事件发生的次数,β代表事件发生一次的概率,那么这α个事件的时间之和服从伽马分布。其概率密度函数为
均值
方差
2.8 瑞利分布
当一个随机二维向量的两个分量呈独立的、均值为0,有着相同的方差的正态分布时,这个向量的模呈瑞利分布,概率密度为:
均值
方差
2.9 莱斯分布
瑞利分布考虑的是零均值实部虚部是独立同分布的复高斯分布,莱斯分布针对的是一般情况下的模值分布,概率密度函数为:
表示直视路径功率分量,
是非直视路径功率分量。
是修正的零阶贝塞尔函数。
2.10 韦布尔分布
适用于机电类产品的磨损累计失效的分布形式。由于它可以利用概率值很容易地推断出它的,被广泛应用于各种寿命试验的数据处理。概率密度函数:
均值
方差
2.11 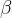 分布
分布
概率密度函数
均值
方差
2.12 对数正态分布
概率密度函数
均值
方差
2.13 柯西分布
概率密度函数
均值和方差不存在。
三、性质及定理
3.1、均值性质
性质1:E (C ) = C
性质2:E (aX ) = a E (X )
性质3:E (X + Y ) = E (X ) + E (Y )
性质4:当X ,Y 相互独立时,E (X Y ) = E (X )E (Y )
性质5:设X 为连续型随机变量,密度函数为f (x),Y = g(X ),若广义积分绝对收敛,则
3.2、方差性质
性质1:若X=C,C为常数,则D(X)=0 .
性质2:若b为常数,随机变量X的方差存在,则bX的方差存在, 且D(bX) = b2D(X)
性质3:若随机变量X1, X2, … , Xn 的方差都存在, 则X1+X2+...+Xn的方差存在,且
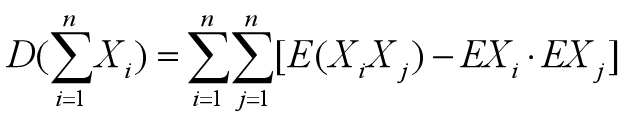
性质4:若随机变量X1, X2, …, Xn相互独立,则
![]()
性质5:有限个相互独立的正态随机变量的线性组合仍然服从正态分布
性质6:切比雪夫(Chebyshev)不等式
对随机变量X 和任意的,有
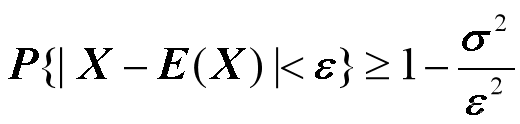
3.3、定理
- 辛钦大数定律
设X1, X2, …是独立同分布的随机变量序列,且E(Xi)=,i=1, 2,…, 则对任给
>0,
辛钦大数定律为估计随机变量的期望值提供了一条实际可行的途径.
- 贝努里大数定律
设Sn是n重贝努里试验中事件A发生的 次数,p是一次试验中事件A发生的概率,则对任给的ε> 0,
贝努里大数定律提供了通过试验来确定事件概率的方法.
- 中心极限定理
设随机序列 {Xj} 独立同分布,有共同的数学期望 和方差
. 部分和Sn =X1+ X2+…+ Xn, 则Sn的标准化
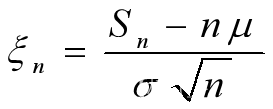
依分布收敛到标准正态分布. 即对任何x,
![]()
这里是标准正态分布的分布函数。对充分大的n ,部分和Sn =X1+ X2+…+ Xn, 的概率分布可以用正态分布
![]()
常用离散型概率分布(下) - 知乎 (zhihu.com)
概率论中,负二项分布(帕斯卡分布)的期望到底是哪个? - 知乎 (zhihu.com)
概率论学习笔记(二) - 知乎 (zhihu.com)
F分布期望方差怎么推导? - 知乎 (zhihu.com)
Gamma分布 - 知乎 (zhihu.com)
瑞利分布(数学名词)_百度百科 (baidu.com)
什么是小尺度衰落信道、瑞利信道、莱斯信道、Nakagami信道 - 知乎 (zhihu.com)
通信原理 高斯分布 莱斯分布 瑞利分布 有何联系 有何区别 如何区分? - 知乎 (zhihu.com)
柯西分布_百度百科 (baidu.com)
贝塔分布_百度百科 (baidu.com)
韦布尔分布_百度百科 (baidu.com)
柯西分布_百度百科 (baidu.com)
总结
本文简单介绍了自己对随机概念的理解,并简单列举了常见的随机分布类型。在信号处理中常用的随机信号模型包括:高斯模型、瑞利模型、莱斯模型等。有更好的内容欢迎在评论区放置链接,另外有问题也欢迎评论区留言。转载请附链接【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主。
相关文章:
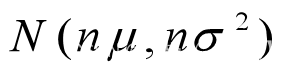
随机分布模型
目录 前言 一、离散型随机变量 1.1 0-1分布 1.2 二项分布 1.3 帕斯卡分布 1.4 几何分布 1.5 超几何分布 1.6 泊松分布 二、连续型随机变量 2.1 均匀分布 2.2 指数分布 2.3 高斯分布/正态分布 2.4 分布(抽样分布) 2.5 t分布(抽样…...

Visual Studio:Entity设置表之间的关联关系
1、选择表并右键-》新增-》关联 2、设置关联的表及关联关系并“确定”即可...

每日五道java面试题之spring篇(二)
目录: 第一题 Spring事务传播机制第二题 Spring事务什么时候会失效?第三题 什么是bean的⾃动装配,有哪些⽅式?第四题 Spring中的Bean创建的⽣命周期有哪些步骤?第五题 Spring中Bean是线程安全的吗? 第一题 Spring事务…...
)
287.【华为OD机试真题】字符串序列判定(贪心算法—JavaPythonC++JS实现)
🚀点击这里可直接跳转到本专栏,可查阅顶置最新的华为OD机试宝典~ 本专栏所有题目均包含优质解题思路,高质量解题代码(Java&Python&C++&JS分别实现),详细代码讲解,助你深入学习,深度掌握! 文章目录 一. 题目-字符串序列判定二.解题思路三.题解代码Python题…...

Sentinel微服务流量治理组件实战上
目录 分布式系统遇到的问题 解决方案 Sentinel 是什么? Sentinel 工作原理 Sentinel 功能和设计理念 流量控制 熔断降级 Sentinel工作主流程 Sentinel快速开始 Sentinel资源保护的方式 基于API实现 SentinelResource注解实现 Spring Cloud Alibaba整合…...
Three.js加载PLY文件
这是官方的例子 three.js webgl - PLY 我在Vue3中使用,测试了好久始终不显示点云数据。在网上查询后发现ply文件要放置在public目录下才行 <el-row><el-button type"primary" class"el-btn" click"IniThree1">PLY</…...

chrome闪退后打不开问题 打开立即闪退
今天刚遇到,大概率是某些网站引起的闪退,重启和清理也不能解决问题 网上到处都是答非所问,还有什么打开chrome再进行设置这种回答 在此解决下 注意该方法根据我测试,唯一会损失的是chrome扩展,可以提前去 C:\Users…...

Slave被误写入数据如何恢复到主库
背景 在GreatSQL主从复制环境中,有时候可能会出现一些误操作,将本应该写入到主库的数据写入到了从库,导致主从数据不一致,影响数据同步。是否可以将写入从库的数据同步写入主库呢? 测试环境 角色IP地址数据库开放端…...

kafka生产者
1.原理 2.普通异步发送 引入pom: <dependencies><dependency><groupId>org.apache.kafka</groupId><artifactId>kafka-clients</artifactId><version>3.0.0</version></dependency><dependency><g…...
前后端分离Vue+node.js在线学习考试系统gqw7o
与其它应用程序相比,在线学习平台的设计主要面向于学校,旨在为管理员和学生、教师、院系提供一个在线学习平台。学生、教师、院系可以通过系统及时查看公告信息等。 在线学习平台是在Windows操作系统下的应用平台。为防止出现兼容性及稳定性问题…...
关于el-select值的回显问题 : 框内显示label值还是value值
<el-form-item label"状态" prop""><el-selectv-model"roleForm.state"class"m-2"size"large"style"width: 240px"placeholder"请选择状态"value-key"value"//value-key 与下面的ke…...
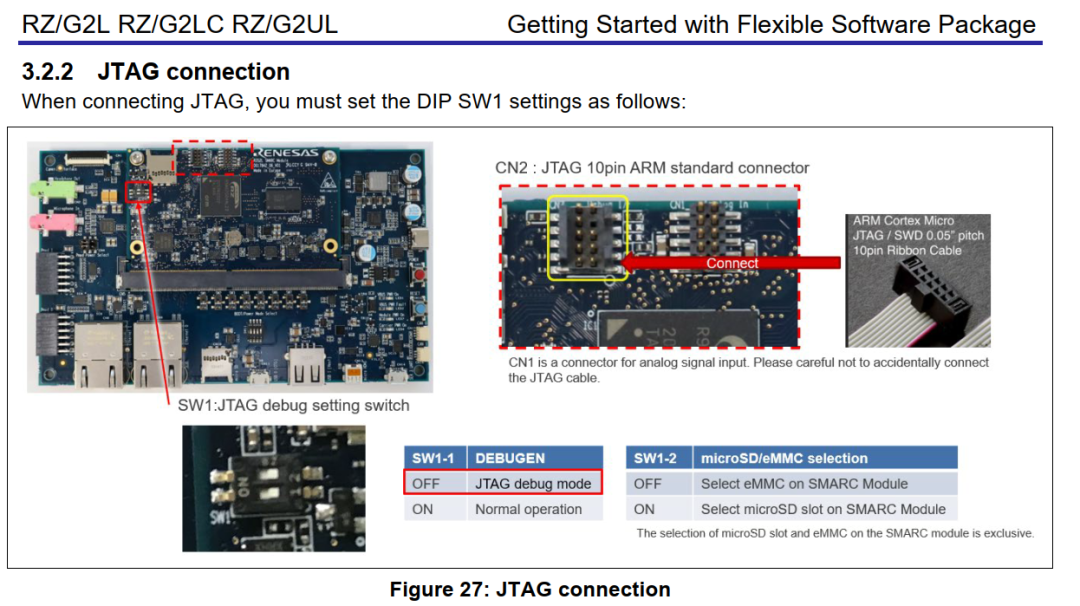
MCU多核异构通信原理
摘要: 本文结合瑞萨RZ/G2L 多核处理器,给大家讲述一下多核异构设计及通信的原理。 随着电子技术的不断发展,以及市场需求的日益增长,嵌入式系统不仅要求执行复杂的控制任务,还需要实时地采集和处理数据。 为了满足这…...
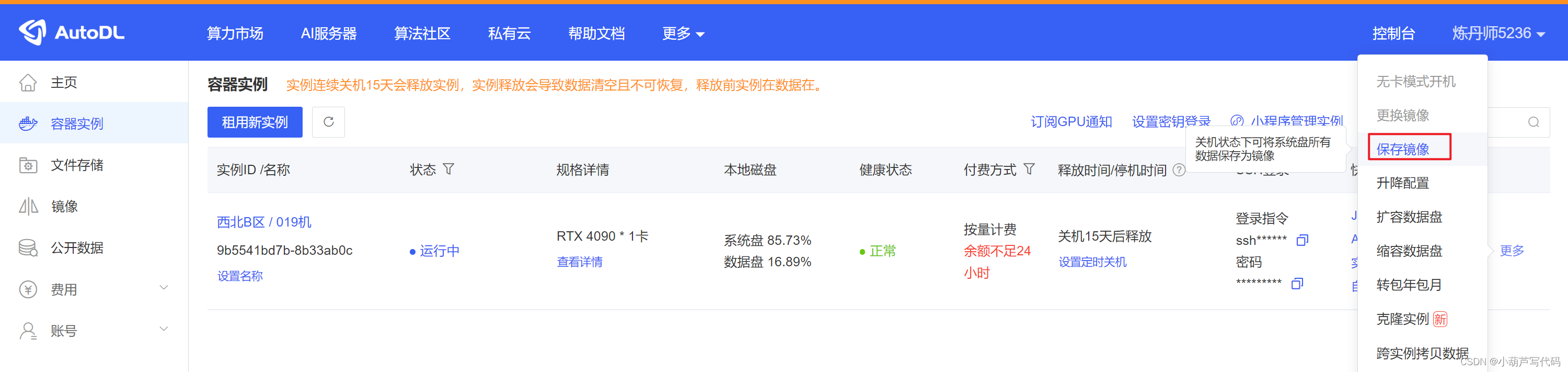
在autodl搭建stable-diffusion-webui+sadTalker
本文介绍在autodl.com搭建gpu服务器,实现stable-diffusion-webuisadTalker功能,图片音频 可生成视频。 autodl租GPU 自己本地部署SD环境会遇到各种问题,网络问题(比如huggingface是无法访问),所以最好的方…...

【办公类-16-10-01】“2023下学期 中4班 自主游戏观察记录(python 排班表系列)
背景需求 上学期的周安排里,每班每周的自主游戏会轮到多个不同的内容 因此在每周的自主游戏观察有2次记录,观察的项目可以写不一样的, 如一位老师写沙水游戏,另一位写表演游戏 本学期,中班的自主游戏全部是户外的&am…...

机器学习:SVM算法(Python)
一、核函数 kernel_func.py import numpy as npdef linear():"""线性核函数:return:"""def _linear(x_i, x_j):return np.dot(x_i, x_j)return _lineardef poly(degree3, coef01.0):"""多项式核函数:param degree: 阶次:param …...

基于yolov5的人脸口罩检测,可进行图像目标检测,也可进行视屏和摄像检测(pytorch框架)【python源码+UI界面+功能源码详解】
功能演示: 基于yolov5的人脸口罩检测系统,支持图像检测,视频检测和实时摄像检测功能(pytorch框架)_哔哩哔哩_bilibili (一)简介 基于yolov5的人脸口罩检测系统是在pytorch框架下实现的&#…...
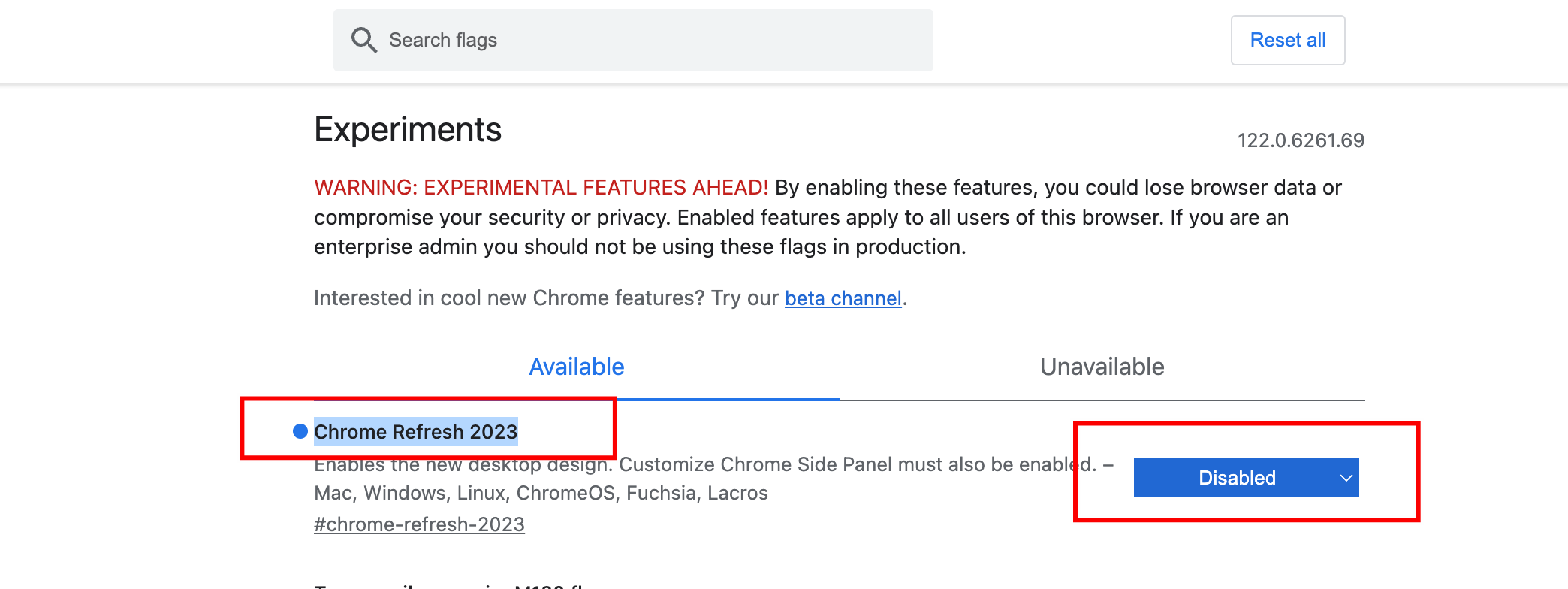
2024如何恢复旧版的Chrome的主题样式
起因 chrome 更新版本之后的主题样式变成了浅紫色的页签卡样式,感觉很不习惯,也很不喜欢 如何换回旧版主题 通过主题商店,安装旧版本的主题 主题商店搜索下面,或着直接访问下面的地址 Chrome Original White Theme https://…...
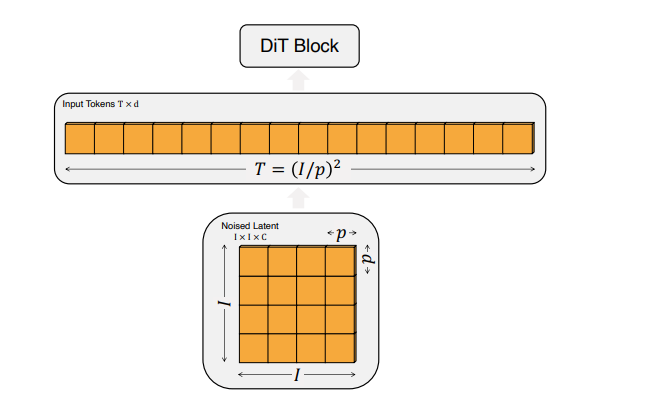
【文生视频】Diffusion Transformer:OpenAI Sora 原理、Stable Diffusion 3 同源技术
文生视频 Diffusion Transformer:Sora 核心架构、Stable Diffusion 3 同源技术 提出背景输入输出生成流程变换器的引入Diffusion Transformer (DiT)架构Diffusion Transformer (DiT)总结 OpenAI Sora 设计思路阶段1: 数据准备和预处理阶段2: 架构设计阶段3: 输入数据…...
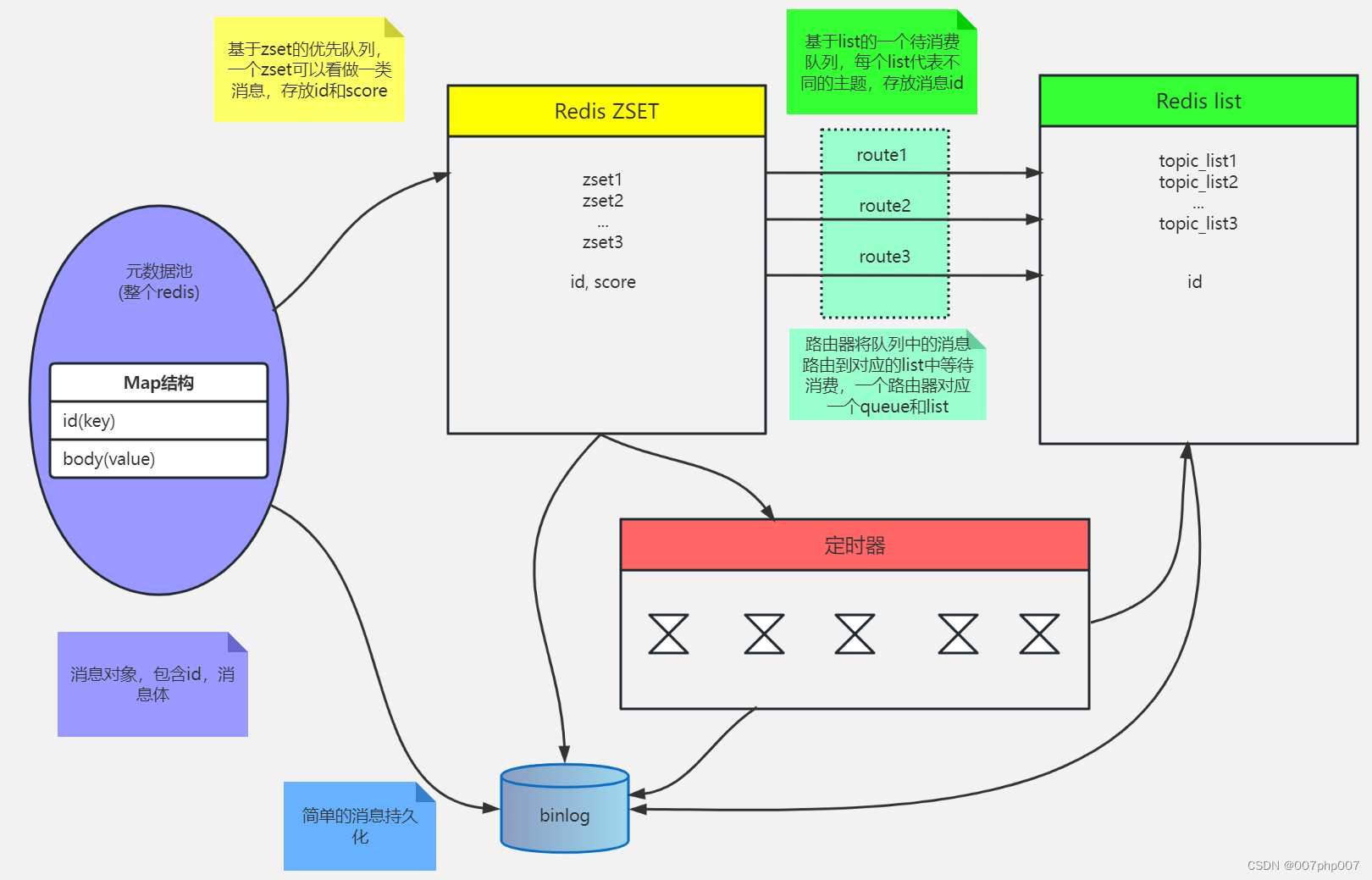
Redis 服务集群、哨兵、缓存及持久化的实现原理和应用场景
Redis 是一种高性能的键值存储系统,已经成为了许多企业和互联网公司的核心技术之一。本文将介绍 Redis 的服务集群、哨兵以及缓存实现原理和应用场景,以帮助读者更好地理解和使用 Redis。 引言: 随着互联网应用规模不断扩大,Redi…...

通过Redis增减库存避坑
问题: 先执行get获取值,判断符合条件再执行incr、decr操作。在临界缓存失效的情况下,会默认赋值当前key为永不过期的0,再执行加减法,导致程序异常。 推荐解决方案: 1、限制接口频率:先incr&…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
