在autodl搭建stable-diffusion-webui+sadTalker
本文介绍在autodl.com搭建gpu服务器，实现stable-diffusion-webui+sadTalker功能，图片+音频 可生成视频。
autodl租GPU
自己本地部署SD环境会遇到各种问题，网络问题（比如huggingface是无法访问），所以最好的方式是租用GPU，可以通过以下视频了解如何使用autodl.com
AutoDL算力云 | 弹性、好用、省钱。租GPU就上AutoDL
炼丹平台AutoDL的简单使用_哔哩哔哩_bilibili
autoDL比较好的点就是上边有很多大佬已经部署好的环境镜像，直接使用就行。
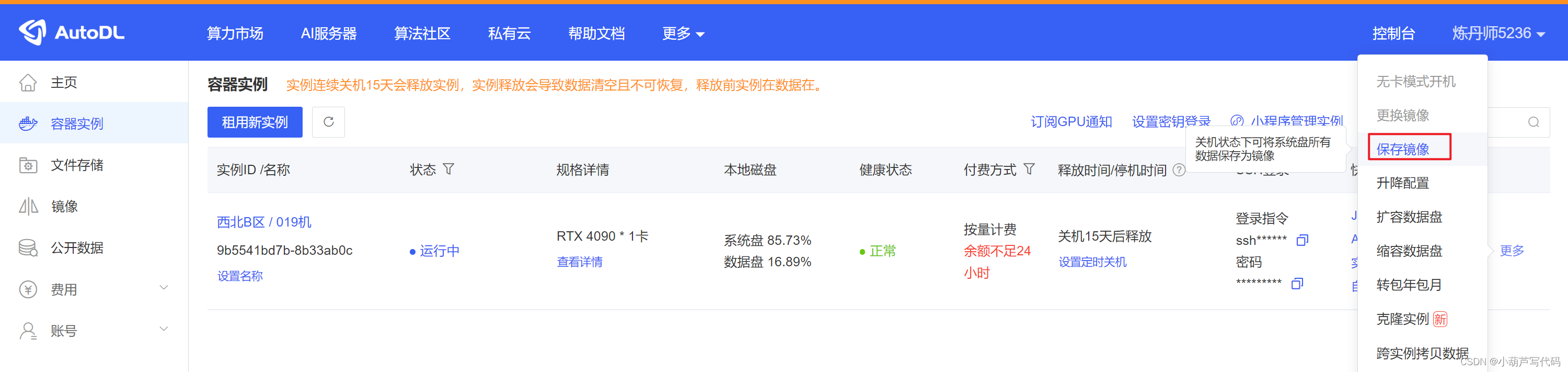
如图是我租用的一个GPU实例。
选择的镜像是 小李xiaolxl AUTOMATIC1111/stable-diffusion-webui的v15.3版本。
镜像使用说明见大佬的视频介绍：
AI绘画云端部署-整合版4.0正式发布 | 全新重构启动3.0 | 全流程教程_哔哩哔哩_bilibili
安装SadTalker
SadTalker git 点击这里。
sadTalker插件安装
stable-diffusion-webui安装SadTalker插件的方式很多，我这里使用从url安装的方式。
别忘了开启加速
插件安装成功后，开始下载模型。
模型下载
SadTalker需要两种模型，checkpoints和gfpgan。下载方式推荐如下两种。
从git下载
阿里云魔搭下载
魔搭社区
模型下载好，需要将模型放到GPU服务器上。
autodl.com支持直接从云盘把文件拷贝到实例，详细可参考如下：
AutoDL帮助文档
我用的是阿里云盘，因为百度云盘的鉴权比骄麻烦。我这边实测如果从阿里云盘拷贝模型到autodl.com,速度能达到10MB/s以上。
模型文件放置的位置如下：
stable-diffusioni-webui/SadTalker下建立两个文件夹，checkpoints和gfpgan
这里有个要注意的点：模型文件的权限都要改成777（chmod -R 777 ./*）,因为sd-webui启动时会切换到其他的user，如果模型文件没有访问权限，就会重新发起模型下载
重启webui
在extension里点击 apply and quit，就会重启webui重新加载。
测试生成视频
sadTalker的使用方式是 图片+声音 生成视频。
文字转语音工具
我使用的微信小程序，搜索：配音家，使用很方便，文字输入就能导出音频。
测试生成视频
保存当前镜像
autodl.com支持把当前的环境保存成自己的镜像，以后自己直接使用，非常方便。
相关文章：
在autodl搭建stable-diffusion-webui+sadTalker
本文介绍在autodl.com搭建gpu服务器，实现stable-diffusion-webuisadTalker功能，图片音频 可生成视频。 autodl租GPU 自己本地部署SD环境会遇到各种问题，网络问题（比如huggingface是无法访问），所以最好的方…...
【办公类-16-10-01】“2023下学期 中4班 自主游戏观察记录（python 排班表系列）
背景需求 上学期的周安排里，每班每周的自主游戏会轮到多个不同的内容 因此在每周的自主游戏观察有2次记录，观察的项目可以写不一样的， 如一位老师写沙水游戏，另一位写表演游戏 本学期，中班的自主游戏全部是户外的&am…...
机器学习：SVM算法（Python）
一、核函数 kernel_func.py import numpy as npdef linear():"""线性核函数:return:"""def _linear(x_i, x_j):return np.dot(x_i, x_j)return _lineardef poly(degree3, coef01.0):"""多项式核函数:param degree: 阶次:param …...
基于yolov5的人脸口罩检测，可进行图像目标检测，也可进行视屏和摄像检测（pytorch框架）【python源码+UI界面+功能源码详解】
功能演示： 基于yolov5的人脸口罩检测系统，支持图像检测，视频检测和实时摄像检测功能（pytorch框架）_哔哩哔哩_bilibili （一）简介 基于yolov5的人脸口罩检测系统是在pytorch框架下实现的&#…...
2024如何恢复旧版的Chrome的主题样式
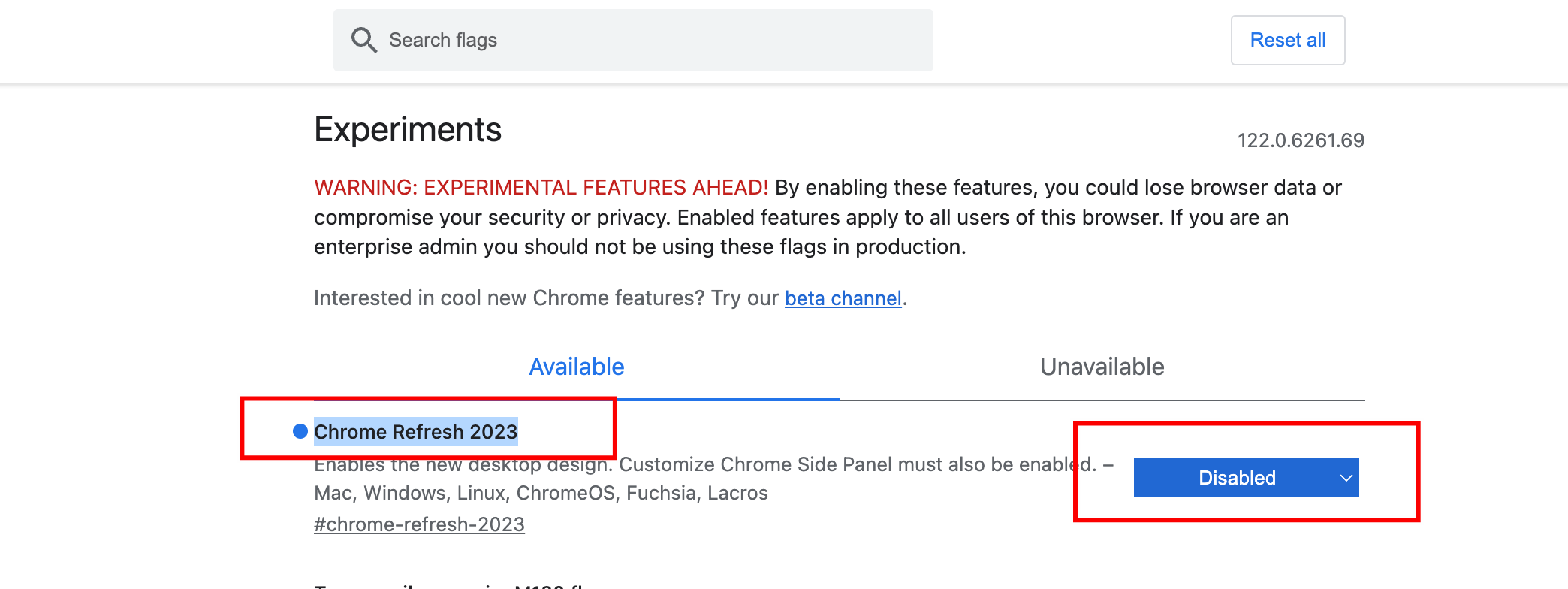
起因 chrome 更新版本之后的主题样式变成了浅紫色的页签卡样式，感觉很不习惯，也很不喜欢 如何换回旧版主题 通过主题商店，安装旧版本的主题 主题商店搜索下面，或着直接访问下面的地址 Chrome Original White Theme https://…...
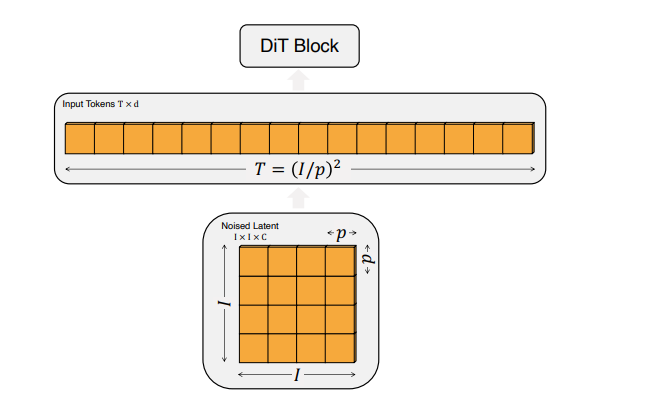
【文生视频】Diffusion Transformer：OpenAI Sora 原理、Stable Diffusion 3 同源技术
文生视频 Diffusion Transformer：Sora 核心架构、Stable Diffusion 3 同源技术 提出背景输入输出生成流程变换器的引入Diffusion Transformer (DiT)架构Diffusion Transformer (DiT)总结 OpenAI Sora 设计思路阶段1: 数据准备和预处理阶段2: 架构设计阶段3: 输入数据…...
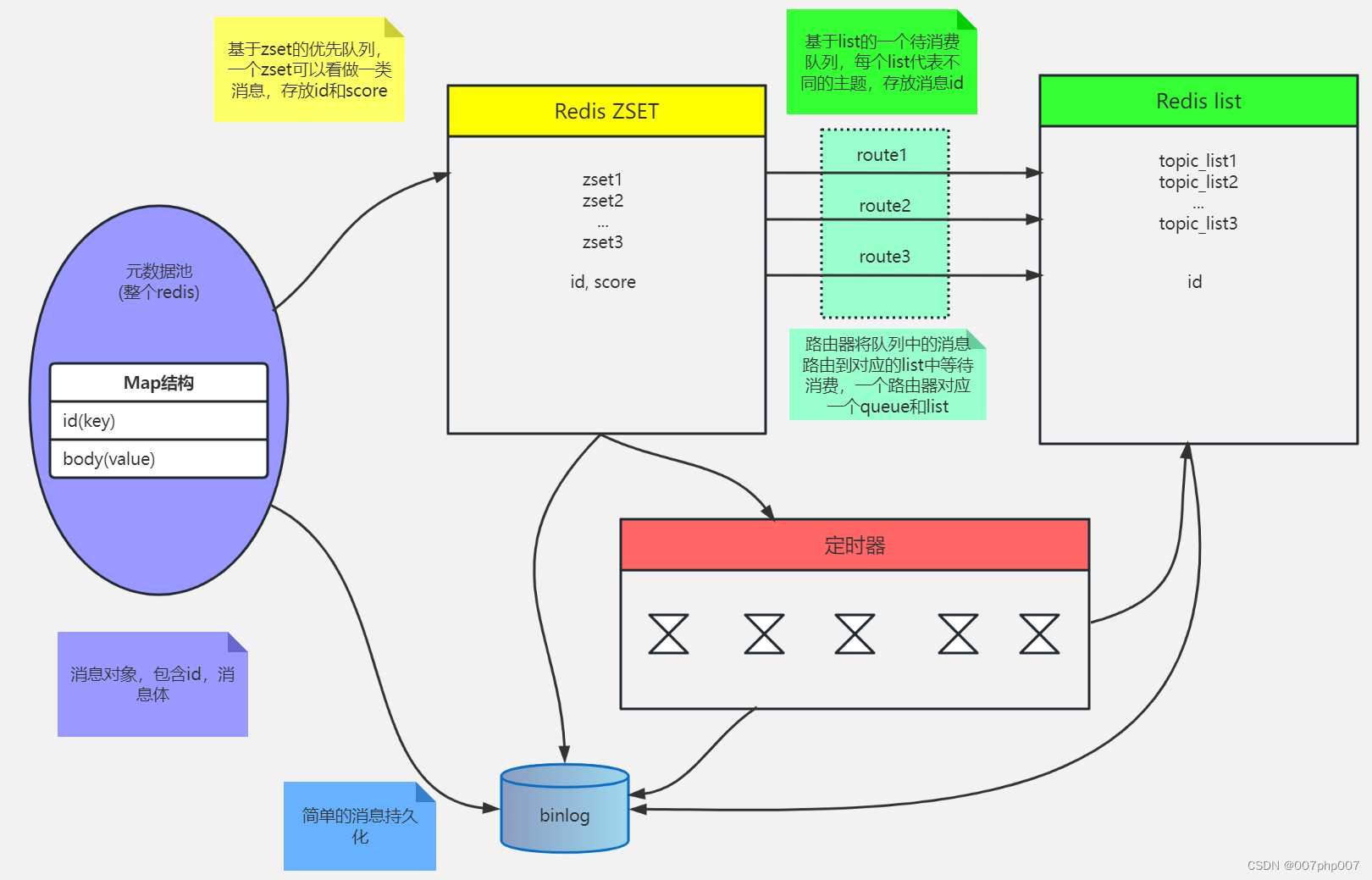
Redis 服务集群、哨兵、缓存及持久化的实现原理和应用场景
Redis 是一种高性能的键值存储系统，已经成为了许多企业和互联网公司的核心技术之一。本文将介绍 Redis 的服务集群、哨兵以及缓存实现原理和应用场景，以帮助读者更好地理解和使用 Redis。 引言： 随着互联网应用规模不断扩大，Redi…...
通过Redis增减库存避坑
问题： 先执行get获取值，判断符合条件再执行incr、decr操作。在临界缓存失效的情况下，会默认赋值当前key为永不过期的0，再执行加减法，导致程序异常。 推荐解决方案： 1、限制接口频率：先incr&…...
Windows系统搭建Elasticsearch引擎结合内网穿透实现远程连接查询数据
文章目录 系统环境1. Windows 安装Elasticsearch2. 本地访问Elasticsearch3. Windows 安装 Cpolar4. 创建Elasticsearch公网访问地址5. 远程访问Elasticsearch6. 设置固定二级子域名 Elasticsearch是一个基于Lucene库的分布式搜索和分析引擎，它提供了一个分布式、多…...
Java爬虫使用JSoup获取静态资源图片
import org.jsoup.Connection; import org.jsoup.Jsoup; import org.jsoup.nodes.Document; import org.jsoup.nodes.Element; import org.jsoup.select.Elements; import java.io.FileOutputStream;/*** 获取静态图片*/public class ImageDownloader {public static void main…...
LeetCode 2433.找出前缀异或的原始数组
给你一个长度为 n 的 整数 数组 pref 。找出并返回满足下述条件且长度为 n 的数组 arr ： pref[i] arr[0] ^ arr[1] ^ … ^ arr[i]. 注意 ^ 表示 按位异或（bitwise-xor）运算。 可以证明答案是 唯一 的。 示例 1： 输入…...
C++面试：系统网络性能评估与优化
系统网络性能评估与优化是指对计算机系统中的网络部分进行评估分析，并采取一系列措施来提升网络性能的能力。在面试中，涉及这一主题的问题可能会围绕以下几个方面展开。 网络性能评估 基于网络延迟、带宽、吞吐量等指标对网络性能进行评估。使用工具&a…...
Java适配器模式 - 灵活应对不匹配的接口
Java适配器模式 - 灵活应对不匹配的接口 引言： 在软件开发中，我们经常遇到不同系统、库或框架之间的接口不兼容问题。为了解决这些问题，我们可以使用适配器模式。适配器模式是一种结构型设计模式，它允许不兼容的接口之间进行协作…...
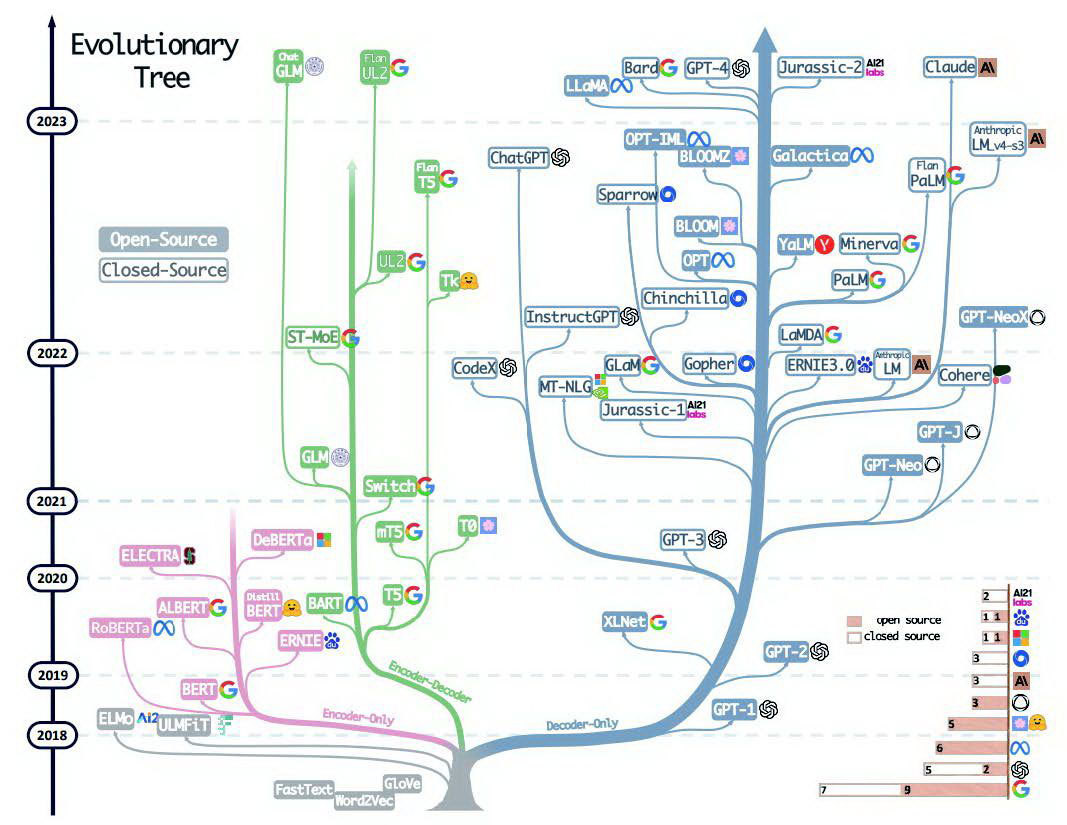
[ai笔记12] chatGPT技术体系梳理+本质探寻
欢迎来到文思源想的ai空间，这是技术老兵重学ai以及成长思考的第12篇分享！ 这周时间看了两本书，一本是大神斯蒂芬沃尔弗拉姆学的《这就是ChatGPT》,另外一本则是腾讯云生态解决方案高级架构师宋立恒所写的《AI制胜机器学习极简入门》…...
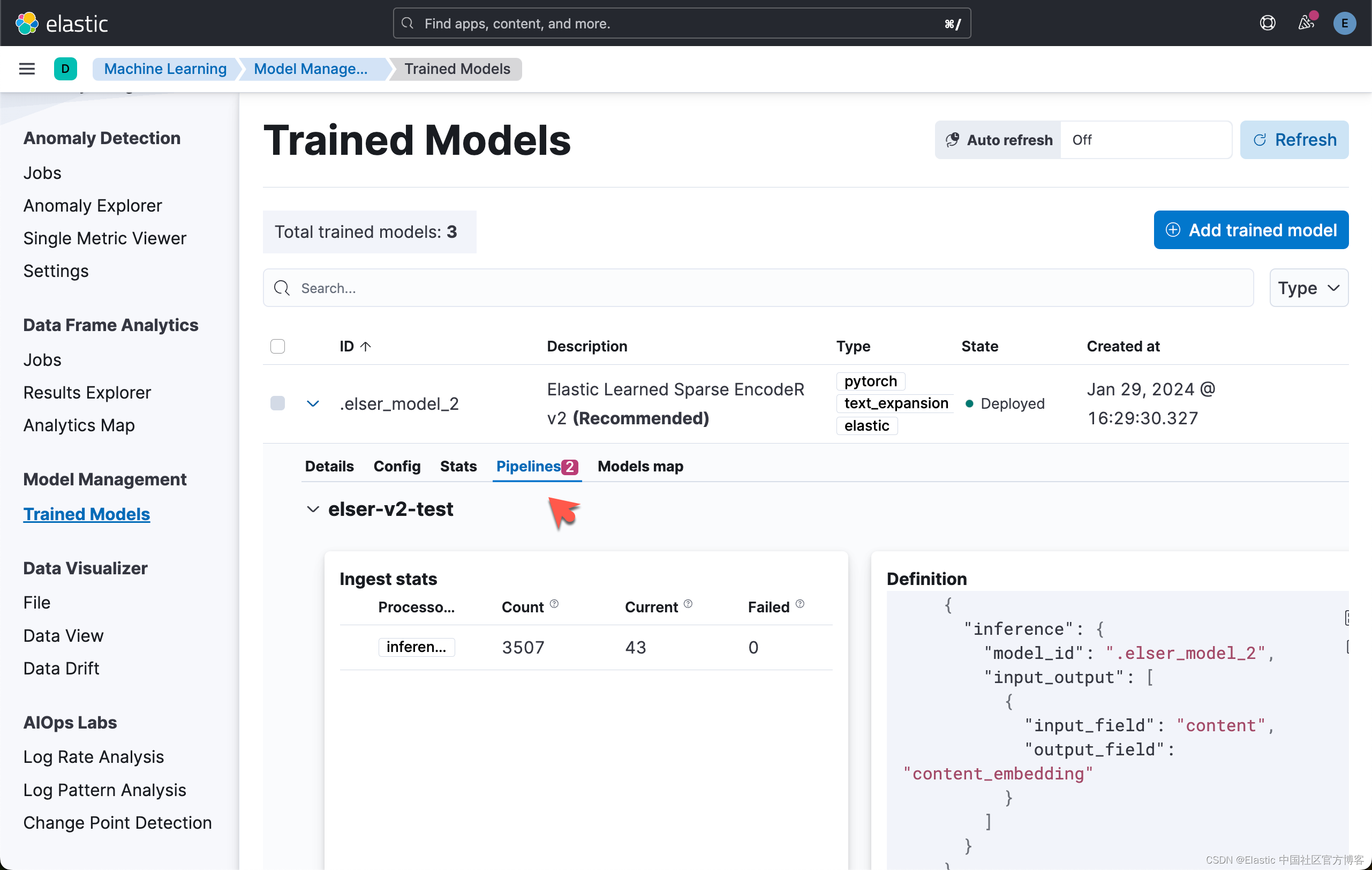
Elasticsearch：使用 ELSER v2 进行语义搜索
在我之前的文章 “Elasticsearch：使用 ELSER 进行语义搜索”，我们展示了如何使用 ELESR v1 来进行语义搜索。在使用 ELSER 之前，我们必须注意的是： 重要：虽然 ELSER V2 已正式发布，但 ELSER V1 仍处于 [预览…...
智慧农业之智能物流
智慧物流属于农业生产环节中的重要节点，上游为农业生产环节，下游为销售与商贸环节，因此，通过联通生产与销售环节，通过合理调配物流过程，可以实现对于农产品的快速运输与销售，减少中间环节中的无效损耗，从而实现增收节支，实实在在地解决了农产品利润偏低的问题。 生产…...
Redis主从、哨兵、Redis Cluster集群架构
Redis主从、哨兵、Redis Cluster集群架构 Redis主从架构 Redis主从架构搭建 主从搭建的问题 如果同步数据失败，查看log日志报错无法连接，检查是否端口未开放出现”Error reply to PING from master:...“日志，修改参数protected-mode no …...
Javascript 运算符、流程控制语句和数组
【三】运算符 【1】算数运算符 （1）分类 加减乘除：*/取余：%和python不一样的点：没有取整// （2）特殊的点 只要NaN参与运算得到的结果也是NaNnull转换成0，undefined转换成NaN 【2…...
电机驱动死区时间
电机驱动死区时间 电机驱动死区时间死区时间（Dead Time）自己话补充说明 电机驱动死区时间 电机驱动死区时间一般在几纳秒到几微秒之间，具体长度取决于所使用的电子器件。 一、什么是电机驱动死区时间？ 电机驱动死区时间指的是在电…...
图像的压缩感知的MATLAB实现（第3种方案）
前面介绍了两种不同的压缩感知实现： 图像压缩感知的MATLAB实现（OMP） 压缩感知的图像仿真（MATLAB源代码） 上述两种方法还存在着“速度慢、精度低”等不足。 本篇介绍一种新的方法。 压缩感知（Compressed S…...
Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题： 下面创建一个简单的Flask RESTful API示例。首先，我们需要创建环境，安装必要的依赖，然后…...
【Linux】shell脚本忽略错误继续执行
在 shell 脚本中，可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行，可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令，并忽略错误 rm somefile…...
解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上，所以报错，到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本，cu、torch、cp 的版本一定要对…...
高防服务器能够抵御哪些网络攻击呢？
高防服务器作为一种有着高度防御能力的服务器，可以帮助网站应对分布式拒绝服务攻击，有效识别和清理一些恶意的网络流量，为用户提供安全且稳定的网络环境，那么，高防服务器一般都可以抵御哪些网络攻击呢？下面…...
dify打造数据可视化图表
一、概述 在日常工作和学习中，我们经常需要和数据打交道。无论是分析报告、项目展示，还是简单的数据洞察，一个清晰直观的图表，往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server，由蚂蚁集团 AntV 团队…...
比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程，两张表是相同的结构，都有整型主键id字段，需要每次从数据库分批取得2000条数据，用于比较，比较操作的同时可以再取2000条数据，等上一次比较完成之后，开始比较，直到比较完所有的数据。比较操作需要比较…...
Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上，对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...
React从基础入门到高级实战：React 实战项目 - 项目五：微前端与模块化架构
React 实战项目：微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇！在前 29 篇文章中，我们从 React 的基础概念逐步深入到高级技巧，涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
Vue 3 + WebSocket 实战：公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战：公司通知实时推送功能详解 📌 收藏 点赞 关注，项目中要用到推送功能时就不怕找不到了！ 实时通知是企业系统中常见的功能，比如：管理员发布通知后，所有用户…...
机器学习的数学基础：线性模型
线性模型 线性模型的基本形式为： f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法，得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...