时间序列分析实战(四):Holt-Winters建模及预测
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 目的
- 2 Holt-Winters三参数指数平滑乘法模型
- 3 Holt-Winters三参数指数平滑乘法模型预测
1 目的
该篇文章主要展示针对时序进行Holt-Winters建模,案例数据同 时间序列分析实战(三):时序因素分解法:某欧洲小镇1963年1月至1976年12月每月旅馆入住的房间数构成时间序列 x t x_t xt。
2 Holt-Winters三参数指数平滑乘法模型
通过上一篇 Blog 知道该时序数据具有季节效应,并且具有长期趋势,考虑首先建立Holt-Winters三参数指数平滑乘法模型:
x t = [ a ( t ) + b ( t ) ] c ( t ) x_t=[a(t)+b(t)]c(t) xt=[a(t)+b(t)]c(t)
运行程序:
fit1=HoltWinters(data1,seasonal = "mult")
fit1
运行结果:
## Holt-Winters exponential smoothing with trend and multiplicative seasonal component.
##
## Call:
## HoltWinters(x = data1, seasonal = "mult")
##
## Smoothing parameters:
## alpha: 0.01567674
## beta : 0.008068444
## gamma: 0.4392594
##
## Coefficients:
## [,1]
## a 875.5123349
## b 1.9568538
## s1 0.9301067
## s2 0.8613974
## s3 0.8741871
## s4 0.9798006
## s5 0.9624445
## s6 1.0964284
## s7 1.2846348
## s8 1.3110818
## s9 1.0004965
## s10 0.9987417
## s11 0.8628932
## s12 0.9793806
基于R最优拟合原则得到平滑系数 α \alpha α=0.01567674, β \beta β=0.008068444, γ \gamma γ=0.4392594。经迭代得到三个参数的最后迭代值: a ( t ) a(t) a(t)=875.5123349, b ( t ) b(t) b(t)=1.9568538,参数 c ( t ) c(t) c(t)的最后12个月估计值对应的是12个月的季节指数,见表1。
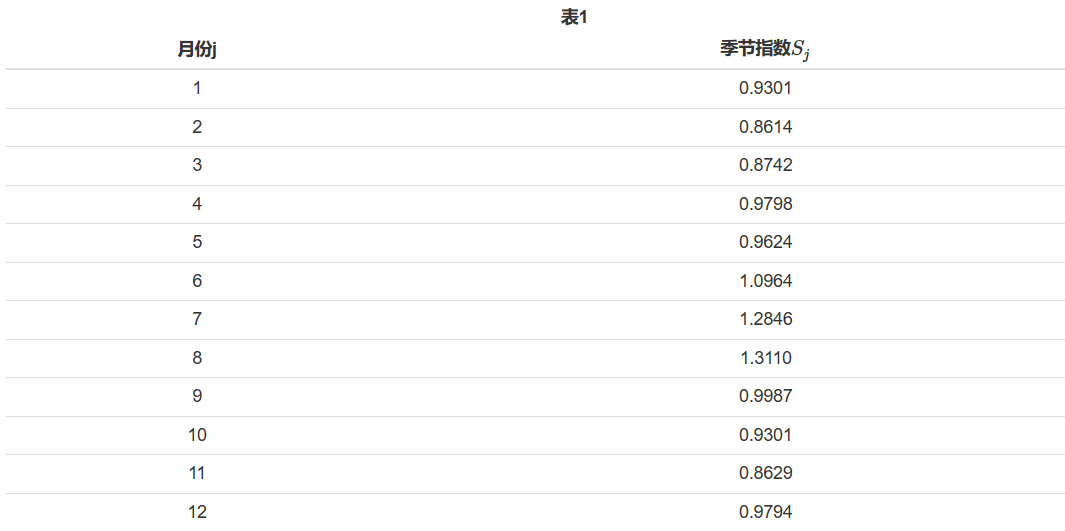
该序列向前任意 k k k期的预测值为:
x ^ t + k = ( 875.512 + 1.967 k ) S j , ∀ k ≥ 1 \hat x_{t+k}=(875.512+1.967k)S_j,\forall k≥1 x^t+k=(875.512+1.967k)Sj,∀k≥1
式中, j j j为 t + k t+k t+k期对应的季节。
3 Holt-Winters三参数指数平滑乘法模型预测
运行程序:
library(forecast)
fore1=forecast::forecast(fit1,h=36)
fore1$mean
运行结果:
## Jan Feb Mar Apr May Jun Jul
## 1977 816.1400 757.5353 770.4935 865.4968 852.0489 972.8099 1142.3105
## 1978 837.9810 777.7629 791.0214 888.5047 874.6492 998.5565 1172.4766
## 1979 859.8220 797.9904 811.5493 911.5126 897.2496 1024.3031 1202.6427
## Aug Sep Oct Nov Dec
## 1977 1168.3931 893.5675 893.9546 774.0477 880.4578
## 1978 1199.1802 917.0614 917.4073 794.3104 903.4559
## 1979 1229.9674 940.5553 940.8600 814.5731 926.4540
运行程序:
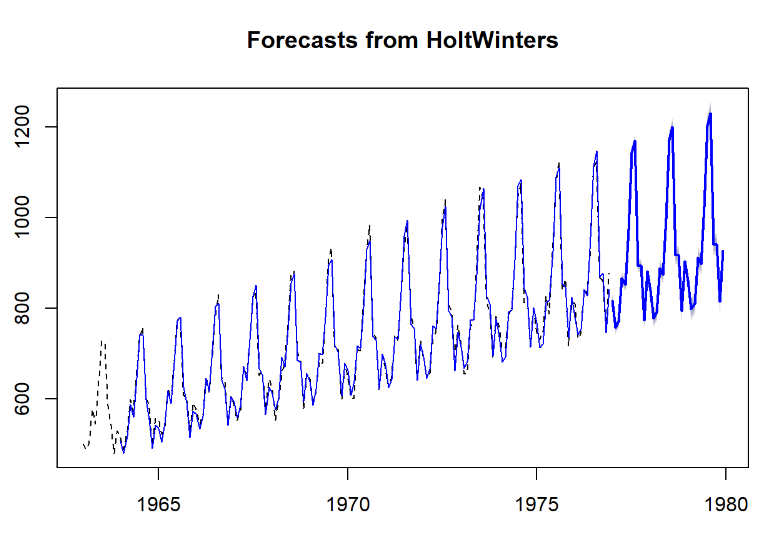
plot(fore1,lty=2,sub='图1 入住房间数序列Holt-Winters三参数指数平滑预测效果图')
lines(fore1$fitted,col=4)
运行结果:
相关文章:

时间序列分析实战(四):Holt-Winters建模及预测
🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972 个人介绍: 研一|统计学|干货分享 擅长Python、Matlab、R等主流编程软件 累计十余项国家级比赛奖项,参与研究经费10w、40w级横向 文…...

Springboot之集成MongoDB无认证与开启认证的配置方式
Springboot之集成MongoDB无认证与开启认证的配置方式 文章目录 Springboot之集成MongoDB无认证与开启认证的配置方式1. application.yml中两种配置方式1. 无认证集成yaml配置2. 有认证集成yaml配置 2. 测试1. 实体类2. 单元测试3. 编写Controller测试 1. application.yml中两种…...

BLEU: a Method for Automatic Evaluation of Machine Translation
文章目录 BLEU: a Method for Automatic Evaluation of Machine Translation背景和意义技术原理考虑 n n n - gram中 n 1 n1 n1 的情况考虑 n n n - gram中 n > 1 n\gt 1 n>1 的情况考虑在文本中的评估初步实验评估和结论统一不同 n n n 值下的评估数值考虑句子长度…...

代码随想录算法训练营|day42
第九章 动态规划 416.分割等和子集代码随想录文章详解 背包类型求解方法0/1背包外循环nums,内循环target,target倒序且target>nums[i]完全背包外循环nums,内循环target,target正序且target>nums[i]组合背包外循环target,内循环nums,target正序且target>nums[i] 416.分…...
vscode与vue/react环境配置
一、下载并安装VScode 安装VScode 官网下载 二、配置node.js环境 安装node.js 官网下载 会自动配置环境变量和安装npm包(npm的作用就是对Node.js依赖的包进行管理),此时可以执行 node -v 和 npm -v 分别查看node和npm的版本号: 配置系统变量 因为在执…...

Vue前端对请假模块——请假开始时间和请假结束时间的校验处理
开发背景:Vueelement组件开发 业务需求:用户提交请假申请单,请假申请的业务逻辑处理 实现:用户选择开始时间需要大于本地时间,不得大于请假结束时间,请假时长根据每日工作时间实现累加计算 页面布局 在前…...

搭建freqtrade量化交易机器人
本文采用python量化机器人框架 freqtrade 开始操作! freqtrade官方文档 官方文档内容过多,请先跟随本文入门阅读,后续深入学习可参考官方文档~ 1. 准备云服务器 docker 环境 这里以云服务器选择 ubuntu 系统开始,先…...

php伪协议 [SWPUCTF 2022 新生赛]ez_ez_php(revenge)
打开题目 题目源代码如下 <?php error_reporting(0); if (isset($_GET[file])) {if ( substr($_GET["file"], 0, 3) "php" ) {echo "Nice!!!";include($_GET["file"]);} else {echo "Hacker!!";} }else {highlight_fi…...
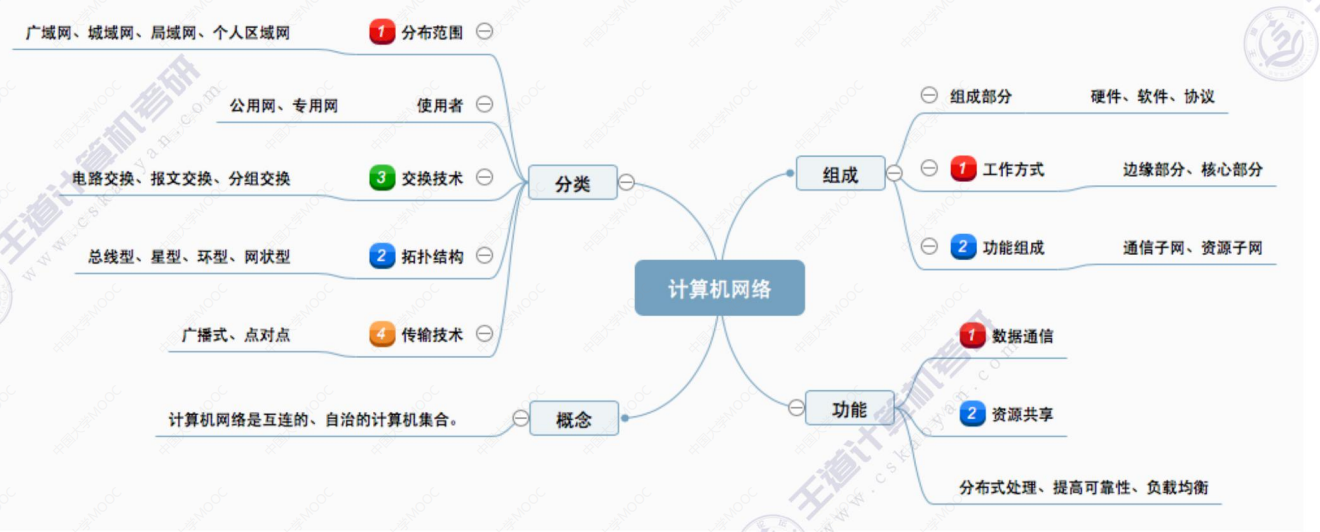
1.1_1 计算机网络的概念、功能、组成和分类
文章目录 1.1_1 计算机网络的概念、功能、组成和分类(一)计算机网络的概念(二)计算机网络的功能(三)计算机网络的组成1.组成部分2.工作方式3.功能组成 (四)计算机网络的分类 总结 1.…...

pytorch中的各种计算
对tensor矩阵的维度变换,加减乘除等是深度学习中的常用操作,本文对一些常用方法进行总结 矩阵乘法 混合矩阵相乘,官网 torch.matmul(input, other, *, outNone) → Tensor这个方法执行矩阵相乘操作,需要第一个矩阵的最后一个维度…...
大数据技术之 Kafka
大数据技术之 Kafka 文章目录 大数据技术之 Kafka第 1 章 Kafka 概述1.1 定义1.2 消息队列1.2.1 传统消息队列的应用场景1.2.2 消息队列的两种模式 1.3 Kafka 基础架构 第 2 章 Kafka 快速入门2.1 安装部署2.1.1 集群规划2.1.2 集群部署2.1.3 集群启停脚本 2.2 Kafka 命令行操作…...
【GB28181】wvp-GB28181-pro部署安装教程(Ubuntu平台)
目录 前言1 安装依赖2 安装MySQL3 安装redis4 编译ZLMediaKit代码及依赖下载编译运行(如果要运行wvp整个项目,这步可以先不执行) 5 编译wvp-pro下载源码(建议从github上下载,gitee上维护有时候不是很同步)编…...

CentOS删除除了最近5个JAR程序外的所有指定Java程序
帮我写一个shell脚本,ps -eo pid,lstart,cmd --sort-start_time | grep "pgz-admin"查到的结果,返回的所有进程PID,第六个之上的,全部kill 当然,你可以创建一个简单的Shell脚本来完成这个任务。以下是一个例…...
面试redis篇-13Redis为什么那么快
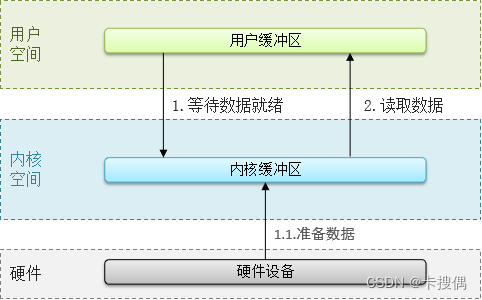
Redis是纯内存操作,执行速度非常快采用单线程,避免不必要的上下文切换可竞争条件,多线程还要考虑线程安全问题使用I/O多路复用模型,非阻塞IOI/O多路复用模型 Redis是纯内存操作,执行速度非常快,它的性能瓶颈是网络延迟而不是执行速度, I/O多路复用模型主要就是实现了高效…...
python Matplotlib Tkinter--pack 框架案例
环境 python:python-3.12.0-amd64 包: matplotlib 3.8.2 pillow 10.1.0 版本一 import matplotlib.pyplot as plt from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg, NavigationToolbar2Tk import tkinter as tk import tkinter.messagebox as messagebox…...

连接未来:嵌入式系统在物联网时代的应用
连接未来:嵌入式系统在物联网时代的应用 随着物联网技术的不断发展,嵌入式系统在物联网时代扮演着至关重要的角色。嵌入式系统作为连接物理世界和数字世界的桥梁,为物联网的实现提供了技术支持和基础设施。以下将从几个方面探讨嵌入式系统在…...

自动驾驶中的障碍物时间对齐法
描述 自动驾驶算法使用的系统往往不是实时系统,因此每个节点间拿到的数据可能不是同一时间的数据,从而造成系统误差,针对这一现象,工程上往往采用时间对齐内插外推法。这里我们用感知障碍物来举例。 自动驾驶系统有许多重要模块…...
介绍 PIL+IPython.display+mtcnn for 音视频读取、标注
1. nn.NLLLoss是如何计算误差的? nn.NLLLoss是负对数似然损失函数,用于多分类问题中。它的计算方式如下:首先,对于每个样本,我们需要将其预测结果通过softmax函数转换为概率分布。softmax函数可以将一个向量映射为一个概率分布&…...
C语言中strstr函数的使用!
strstr函数的作用是什么? 查找子字符串 具体直接看下面的这段代码我相信你必明白 #define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> int main() { char *p1 "abcdefghijklmnopqrstuvwxyz"; char* p2 "abc"; char* r…...

Vue项目中,src目录下的vue.app文件介绍
在 Vue 项目中,src 文件夹通常包含了项目的核心代码。在这个文件夹下,App.vue 是一个特殊的文件,它代表了整个 Vue 应用的根组件。 App.vue 是一个单文件组件(Single File Component, 简称 SFC),它允许你将…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...
