HUAWEI Programming Contest 2024(AtCoder Beginner Contest 342)(A,B,C,D,E,F,G)
看不懂的英文,题意很难理解,这场还是有点难度的。
C需要处理,D是不太明显的dijikstra,E是线段树优化dp,F是个不好想的线段树,主席树应该也能做。
我觉得讲的很好的宝藏up主->B站视频讲解。之后会比较忙,一篇上万字的题解太费时间了,之后的题解可能就没办法大段大段的来讲了,只说重点。
A Yay!
题意:
长度大于等于3的字符串里只有两种字符,其中一种字符只出现了一次,找到它的位置。
思路:
我的思路:
如果我们事先知道只出现一次的那个字符是什么,就可以直接用string里内置的 find_first_of() 函数来找位置,或者知道另一种字符,就可以用string里内置的 find_first_not_of() 函数来找位置。
字符串第一个字符一定属于两种字符之一,假设出现了一次的字符为a,出现多次的字符为b。分类讨论:
- 如果第一个字符是a,
find_first_of(str[0],1)会返回string::npos,这时第一个字符就是a - 如果第一个字符是b,
find_first_of(str[0],1)会返回一个合法位置,这时直接find_first_not_of(str[0],1)就能找到a了
jiangly大佬的思路:
使用string内置的 count(str[0]) 函数,如果个数大于1就是b字符,如果个数为1就是a字符
code:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;string str;int main(){cin>>str;if(str.find_first_of(str[0],1)==string::npos)cout<<1;else cout<<str.find_first_not_of(str[0])+1;return 0;
}
B - Which is ahead?
题意:
N N N 个人排成一队,每个人有个编号 P i P_i Pi。有 Q Q Q 次询问,每次询问给出两个编号 A i A_i Ai 和 B i B_i Bi,输出靠前的那个人的编号。
思路:
对每个编号记录它在队列中的位置,之后拿到编号直接查询位置。
code:
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=105;int n,idx[maxn],q;int main(){cin>>n;for(int i=1,t;i<=n;i++){cin>>t;idx[t]=i;}cin>>q;for(int i=1,a,b;i<=q;i++){cin>>a>>b;printf("%d\n",(idx[a]>idx[b])?b:a);}return 0;
}
C - Many Replacement
题意:
给你一个长为 N N N 的小写字母组成的字符串 S S S。有 Q Q Q 次询问,每次询问给出两个小写字母 c i , d i c_i,d_i ci,di ,表示将字符串中所有 c i c_i ci 字符换成 d i d_i di。问最后得到的字符串是什么。
思路1:
但是发现对每种字符,我们只关心它最后变成了哪种字符,因此用map记录一下这个字符最后变成了什么就行了,也就是这个字符最后映射为什么字符。
更详细的说,一开始每个字符都映射为自己,每次修改把所有映射值为 c i c_i ci 的键值对改成映射为 d i d_i di,最后把原字符串映射一下就行了。时间复杂度 O ( 26 ∗ q ∗ l o g ( 26 ) + n ∗ l o g ( 26 ) ) O(26*q*log(26)+n*log(26)) O(26∗q∗log(26)+n∗log(26))
code1:
#include <iostream>
#include <cstdio>
#include <map>
#include <vector>
#include <cstring>
using namespace std;int n,q;
string str;
map<char,char> mp;
vector<int> a[30];
int c;int main(){cin>>n>>str;for(char ch='a';ch<='z';ch++)mp[ch]=ch;cin>>q;for(int i=1;i<=q;i++){char c1,c2;cin>>c1>>c2;for(char ch='a';ch<='z';ch++)if(mp[ch]==c1)mp[ch]=c2;}for(auto x:str)printf("%c",mp[x]);return 0;
}
思路2:
赛时丑陋的想法。
把每个字符看成一个人,它一开始有把仓库钥匙,仓库里的货物就是原字符串填有这个字符的所有位置。每次进行字符修改的时候,就像把钥匙给了别人,不用动货物。
听着挺直观的,但是不好写。
code2:
#include <iostream>
#include <cstdio>
#include <map>
#include <vector>
#include <cstring>
using namespace std;int n,q;
string str;
map<char,int> mp;
vector<int> a[30];
int c;int main(){cin>>n>>str;for(int i=0;i<n;i++){if(mp.find(str[i])==mp.end())mp[str[i]]=++c;a[mp[str[i]]].push_back(i);}cin>>q;for(int i=1;i<=q;i++){char t1,t2;int n1,n2;cin>>t1>>t2;if(mp.find(t1)==mp.end() || t1==t2)continue;if(mp.find(t2)==mp.end())mp[t2]=mp[t1];else {n1=mp[t1];n2=mp[t2];a[n2].insert(a[n2].end(),a[n1].begin(),a[n1].end());a[n1].clear();}mp.erase(t1);}for(auto x:mp){for(auto idx:a[x.second]){str[idx]=x.first;}}cout<<str;return 0;
}
D - Square Pair
题意:
给你有 N N N 个非负数的数组 A A A,找到有多少对 ( i , j ) (i,j) (i,j) 满足 1 ≤ i < j ≤ N 1\le i<j\le N 1≤i<j≤N 且 A i ∗ B j 是平方数 A_i*B_j是平方数 Ai∗Bj是平方数。
能用非负数的平方表示的非负数就是平方数。
思路:
对平方数进行质因数分解,它的所有质因子的次数都是偶数(这样正好可以对半分),如果两个数乘起来是平方数,那么它们含有的一种质因子的次数的奇偶性一定相同的。我们的任务就是 l o g n logn logn 次内对一个 i i i,统计前面 i − 1 i-1 i−1 个数中满足和这个数每个质因子的次数的奇偶性相同的数的个数。
因为我们只关心奇偶性,所以可以把多余次数的质因数全部去掉,每个奇数次数的质因数只留下一个就行了,比如 108 = 2 ∗ 2 ∗ 3 ∗ 3 ∗ 3 108=2*2*3*3*3 108=2∗2∗3∗3∗3,去重后得到 3 3 3。对处理后的数存入map中就可以 logn 次查询了。
不过要特判 0 0 0 的情况,因为 0 0 0 可以和其他任何数产生有效的一对。如果 0 0 0 的个数有 n u m num num 个,那么答案会多出 n u m ∗ ( n − 1 ) num*(n-1) num∗(n−1),不过 0 和其他 0 会重复算,再减去 n u m ∗ ( n u m − 1 ) / 2 num*(num-1)/2 num∗(num−1)/2。边读数边算边特判也可以。
code:
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
const int maxn=2e5+5;int n;int g(int x){int ans=1;for(int i=2;i*i<=x;i++){if(x%i==0){int cnt=0;while(x%i==0)x/=i,cnt++;if(cnt&1)ans*=i;}}if(x>1)ans*=x;return ans;
}int main(){cin>>n;long long num=0,ans=0;map<int,long long> mp;for(int i=1,t,x;i<=n;i++){cin>>t;if(t==0){num++;continue;}x=g(t);ans+=mp[x];mp[x]++;}cout<<ans+num*(n-1)-num*(num-1)/2<<endl;return 0;
}
E - Last Train
题意:
有 N N N 个火车站, M M M 个火车信息。第 i i i 个火车信息有六个正整数 l i , d i , k i , c i , A i , B i l_i,d_i,k_i,c_i,A_i,B_i li,di,ki,ci,Ai,Bi,表示:
- 在每个时刻 t = l i , l i + d i , l i + 2 ∗ d i , … , l i + ( k i − 1 ) ∗ d i t=l_i,l_i+d_i,l_i+2*d_i,\dots,l_i+(k_i-1)*d_i t=li,li+di,li+2∗di,…,li+(ki−1)∗di,都有一列火车从车站 A i A_i Ai 出发,并在时刻 t + c i t+c_i t+ci 到达车站 B i B_i Bi
问你从车站 i ( 1 ≤ i ≤ N − 1 ) i\quad (1\le i\le N-1) i(1≤i≤N−1) 出发,到达车站 N N N 的最晚的出发时间是多少。
思路:
乍一看不好下手,不妨从终点站来看。
要出发时间最晚,那么我们到达终点站也会很晚。为了在路上留出足够充裕的时间,我们可以假定到达终点站坐的是最后一班车。
这样来考虑的话,我们逆推得到的这些车站也可以通过尽可能晚的车次来从其他车站到达。这样逆推到我们所在的车站,就得到了我们现在要出发的车站最晚可以什么时候走。而且我们一定不会回到已经经过的车站,否则我们再从这个车站出发的话,最晚时间就会变早。
我们每次挑出最晚时间出发的车站进行逆推,把更新的车站再依次进行逆推,其实就相当于在用dijkstra算法跑最短路。
详细的来说。我们一开始读入火车信息的时候反向建边,然后后终点 N N N 开始跑最短路。每次取出出发时刻最晚的车站,如果通过一条边(也就是一班车)可以到达一个点的时间变晚,就加入堆。
如何算出最晚车次是哪一次:假设现在所在的点的最晚时刻是 t m tm tm,那么有 l + ( x − 1 ) ∗ d + c ≤ t m l+(x-1)*d+c\le tm l+(x−1)∗d+c≤tm x ≤ t m − l − c d + 1 x\le\frac{tm-l-c}{d}+1 x≤dtm−l−c+1 x = ⌊ t m − l − c d ⌋ + 1 ( 1 ≤ x ≤ k ) x=\left\lfloor\frac{tm-l-c}{d}\right\rfloor+1\quad(1\le x\le k) x=⌊dtm−l−c⌋+1(1≤x≤k)最后只要保证 x ≥ 1 x\ge 1 x≥1,然后 x x x 取 x x x 与 k k k 的较小值即可。发车时刻 l + ( x − 1 ) ∗ d + c l+(x-1)*d+c l+(x−1)∗d+c 就是我们从目标车站的最晚出发时刻。
code:
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
#define pii pair<ll,ll>
const int maxn=2e5+5;
const ll inf=2e18;int n,m;int head[maxn],cnt;
struct edge{int v,nxt;ll l,d,k,c;
}e[maxn];
void add(int u,int v,ll l,ll d,ll k,ll c){e[++cnt].v=v;e[cnt].l=l;e[cnt].d=d;e[cnt].k=k;e[cnt].c=c;e[cnt].nxt=head[u];head[u]=cnt;
}ll dis[maxn];
bool vis[maxn];
void dijkstra(){for(ll i=1;i<=n;i++)dis[i]=-inf,vis[i]=false;priority_queue<pii> h;dis[n]=inf;h.push(pii(dis[n],n));while(!h.empty()){int dt=h.top().first,u=h.top().second;h.pop();if(vis[u])continue;else vis[u]=true;for(ll i=head[u],v,l,d,k,c,ti,tm;i;i=e[i].nxt){v=e[i].v;l=e[i].l;d=e[i].d;k=e[i].k;c=e[i].c;ti=min(k,(dis[u]-c-l)/d+1);//坐哪一趟车 if(ti<1)continue;tm=l+(ti-1)*d;//发车时间if(dis[v]<tm){dis[v]=tm;h.push(pii(dis[v],v));} }}
}int main(){cin>>n>>m;for(ll i=1,l,d,k,c,a,b;i<=m;i++){cin>>l>>d>>k>>c>>a>>b;add(b,a,l,d,k,c);}dijkstra();for(int i=1;i<n;i++)if(dis[i]!=-inf)printf("%lld\n",dis[i]);else printf("Unreachable\n");return 0;
}
F - Black Jack
题意:
有一个 D D D 面骰子和两个变量 x , y x,y x,y,一开始 x = y = 0 x=y=0 x=y=0
你可以投若干次骰子,并把骰子的值加到 x x x 上。
然后庄家投若干次骰子,并把骰子的值加到 y y y 上。如果某次投骰子后 y > L y>L y>L,庄家就停止投骰子。
如果 x > N x>N x>N ,则你输。如果 x > y x>y x>y 或 y > N y>N y>N 则你赢。两种情况都不是算你输(也就是 x , y > N x,y>N x,y>N)
问你采取最大胜率的策略,胜率是多少。
思路:
jiangly的思路(写法不太一样):
当我们是某个点数的时候,我们可以选择投骰子或者不投。选择哪一个取决于哪个胜率更高。而庄家的策略始终不变,因此庄家投出的每种 y y y 的概率是固定的。
当我们选择投骰子时,那么假设 d p [ i ] dp[i] dp[i] 是我们当前点数为 i i i 时的胜率, 那么 d p [ i ] = ∑ k = i + 1 i + d d p [ k ] ∗ 1 d dp[i]=\sum_{k=i+1}^{i+d}dp[k]*\frac1d dp[i]=∑k=i+1i+ddp[k]∗d1 。如果我们选择不投骰子,假设 f [ i ] f[i] f[i] 表示庄家投出点数为 i i i 的概率,我们的胜率就是 ∑ y = L x − 1 f [ i ] + ∑ y = n + 1 l + d − 1 f [ i ] \sum_{y=L}^{x-1}f[i]+\sum_{y=n+1}^{l+d-1}f[i] ∑y=Lx−1f[i]+∑y=n+1l+d−1f[i](后者表示庄家投出了比 n n n 大的点数,显然这时只要我们的点数不超过 n n n 就行)。两种选择取较大值就是 d p [ i ] dp[i] dp[i] 了。
f f f 数组需要预处理,当算到 f [ i ] f[i] f[i] 时,我们只需要算出前 d d d 个的值,这时可以边算 f f f 数组,边处理一个前缀和数组,这样就可以每次 O ( 1 ) O(1) O(1) 得到区间和,整个预处理过程是 O ( n ) O(n) O(n) 的。不过需要注意的是,庄家投骰子的策略是投到 y > = L y>=L y>=L 就立刻停止,因此前缀和只处理到前 0 ∼ L − 1 0\sim L-1 0∼L−1 ,后面不再加入新 f [ i ] f[i] f[i] 值。 ∑ y = n + 1 l + d − 1 f [ i ] \sum_{y=n+1}^{l+d-1}f[i] ∑y=n+1l+d−1f[i] 这个东西也可以预先直接算出来。之后为了方便处理,我们再处理一个 g [ i ] g[i] g[i] 数组,表示我们投出点数为 i i i 时,庄家的败率(也就是我们选择停手的胜率)。
因为计算 d p dp dp 值时,我们需要后面 d d d 位的 d p dp dp 值,所以从后向前计算。
code:
WA3个点,精度损失严重。
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn=4e5+5;int n,L,d;//上界为n下界为l,面数为d
double f[maxn],g[maxn],s[maxn],lose;
double dp[maxn];int main(){cin>>n>>L>>d;s[0]=f[0]=1;for(int i=1,l,r;i<=n;i++){l=max(0,i-d);r=min(i-1,L-1);f[i]=(s[r]-((l>0)?s[l-1]:0))/d;//庄家投出i的概率 s[i]=s[i-1]+f[i];}for(int i=n+1,l,r;i<L+d;i++){//投出i点 l=max(0,i-d);r=L-1;lose+=(s[r]-((l>0)?s[l-1]:0))/d;}for(int i=0;i<L;i++)f[i]=0;f[0]=lose;for(int i=0;i<n;i++)g[i+1]=g[i]+f[i];//庄家败率 s[n+1]=0;for(int i=n,l,r;i>=0;i--){l=i+1;r=min(i+d,n);dp[i]=max(g[i],(s[l]-s[r+1])/d);s[i]=s[i+1]+dp[i]; }printf("%.15lf\n",dp[0]);return 0;
}
由于前缀和的精度损失比较严重,所以会WA掉三个点,因此采用线段树维护单点修改,区间和查询。
我前缀和调半天还WA三个点,改成线段树还T,而jiangly大佬直接一遍A了。。。
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
const int maxn=2e5+5;int n,L,d;//上界为n下界为l,面数为d
double f[maxn],g[maxn],lose;
double dp[maxn];struct segement_tree{#define ls p<<1#define rs p<<1|1int n;struct Node{double val;}t[maxn<<2];void push_up(int p){t[p].val=t[ls].val+t[rs].val;}void print(int p,int l,int r){printf("%2d:[%2d,%2d] %lf\n",p,l,r,t[p].val);if(l==r)return;int mid=(l+r)>>1;print(ls,l,mid);print(rs,mid+1,r);}void print(){print(1,0,n);}void build(int p,int l,int r){if(l==r){t[p].val=0;return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(p);}void build(int _n){n=_n;build(1,0,n);}void mdy(int p,int l,int r,int x,double val){if(l==r){t[p].val=val;return;}int mid=(l+r)>>1;if(x<=mid)mdy(ls,l,mid,x,val);else mdy(rs,mid+1,r,x,val);push_up(p);}inline void mdy(int id,double val){mdy(1,0,n,id,val);}double query(int p,int l,int r,int L,int R){if(L<=l && r<=R){return t[p].val;}int mid=(l+r)>>1;double ans=0;if(L<=mid)ans+=query(ls,l,mid,L,R);if(R>mid)ans+=query(rs,mid+1,r,L,R);return ans;}inline double query(int l,int r){return query(1,0,n,l,r);}#undef ls#undef rs
}tr;int main(){cin>>n>>L>>d;tr.build(n);f[0]=1;tr.mdy(0,f[0]);for(int i=1,l,r;i<=n;i++){l=max(0,i-d);r=min(i-1,L-1);f[i]=tr.query(l,r)/d;//庄家投出i的概率 tr.mdy(i,f[i]);}for(int i=n+1,l,r;i<L+d;i++){//投出i点 l=max(0,i-d);r=L-1;lose+=tr.query(l,r)/d;}for(int i=0;i<L;i++)f[i]=0;f[0]=lose;for(int i=0;i<n;i++)g[i+1]=g[i]+f[i];//庄家败率 for(int i=n,l,r;i>=0;i--){l=i+1;r=min(i+d,n);dp[i]=max(g[i],(l<=r)?tr.query(l,r)/d:0);tr.mdy(i,dp[i]);}printf("%.15lf\n",dp[0]);return 0;
}
G - Retroactive Range Chmax
题意:
给你有 N N N 个正整数的数组 A A A,有 Q Q Q 次操作,操作有三种:
- 输入
1 l r x:将 A l , A l + 1 , … , A r A_l,A_{l+1},\dots,A_{r} Al,Al+1,…,Ar 的每个数 A i A_i Ai 变成 m a x { A i , x } max\{A_i,x\} max{Ai,x}。 - 输入
2 i:将第 i i i 个操作撤销,保证第 i i i 个操作是第一种操作,并且之前没有被撤销过 - 输入
3 i:查询 A i A_i Ai 的值。
思路:
借鉴这位大佬
相当于记录每个点所有可能的值,显然在某个时刻查询的时候,我们只要给出最大的那个就行了。但是直接暴力存储每个点的可能的值既会爆空间又会爆时间。因此用线段树维护,我们这里的值不需要 push_up 和 push_down 来维护,查询时只需要返回到达 A i A_i Ai 时线段树路径上的最大值就行了。
code:
基本相当于照抄了(汗
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
const int maxn=2e5+5;int n,a[maxn];
int q;struct segement_tree{#define ls p<<1#define rs p<<1|1int n;struct Node{map<int,int> val;}t[maxn<<2];void build(int p,int l,int r){if(l==r){t[p].val[a[l]]++;return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);}void build(int _n){n=_n;build(1,1,n);}void mdy(int p,int l,int r,int L,int R,int d,bool x){if(L<=l && r<=R){if(x){t[p].val[d]++;}else {if(--t[p].val[d]==0)t[p].val.erase(d);}return;}int mid=(l+r)>>1;if(L<=mid)mdy(ls,l,mid,L,R,d,x);if(R>mid)mdy(rs,mid+1,r,L,R,d,x);}int query(int p,int l,int r,int L,int R){if(L<=l && r<=R){return t[p].val.rbegin()->first;}int mid=(l+r)>>1,ans=0;if(!t[p].val.empty())ans=t[p].val.rbegin()->first;if(L<=mid)ans=max(ans,query(ls,l,mid,L,R));if(R>mid)ans=max(ans,query(rs,mid+1,r,L,R));return ans;}#undef ls#undef rs
}tr;struct opter{int l,r,d;
}opt[maxn];int main(){int n;cin>>n;for(int i=1;i<=n;i++)cin>>a[i];tr.build(n);cin>>q;for(int i=1;i<=q;i++){int op;cin>>op;if(op==1){cin>>opt[i].l>>opt[i].r>>opt[i].d;tr.mdy(1,1,n,opt[i].l,opt[i].r,opt[i].d,1);}else if(op==2){cin>>opt[i].d;tr.mdy(1,1,n,opt[opt[i].d].l,opt[opt[i].d].r,opt[opt[i].d].d,0);}else {cin>>opt[i].d;cout<<tr.query(1,1,n,opt[i].d,opt[i].d)<<endl;}}return 0;
}
相关文章:
(A,B,C,D,E,F,G))
HUAWEI Programming Contest 2024(AtCoder Beginner Contest 342)(A,B,C,D,E,F,G)
看不懂的英文,题意很难理解,这场还是有点难度的。 C需要处理,D是不太明显的dijikstra,E是线段树优化dp,F是个不好想的线段树,主席树应该也能做。 我觉得讲的很好的宝藏up主->B站视频讲解。之后会比较忙…...

解决Docker镜像中CentOS 8仓库问题
前言: 在yum执行过程中,持续遇到与CentOS 8上的’appstream’仓库元数据检索相关的错误。具体错误消息为:“错误:下载’appstream’仓库元数据失败:无法准备内部镜像列表:镜像列表中没有URL。” 问题分析&…...
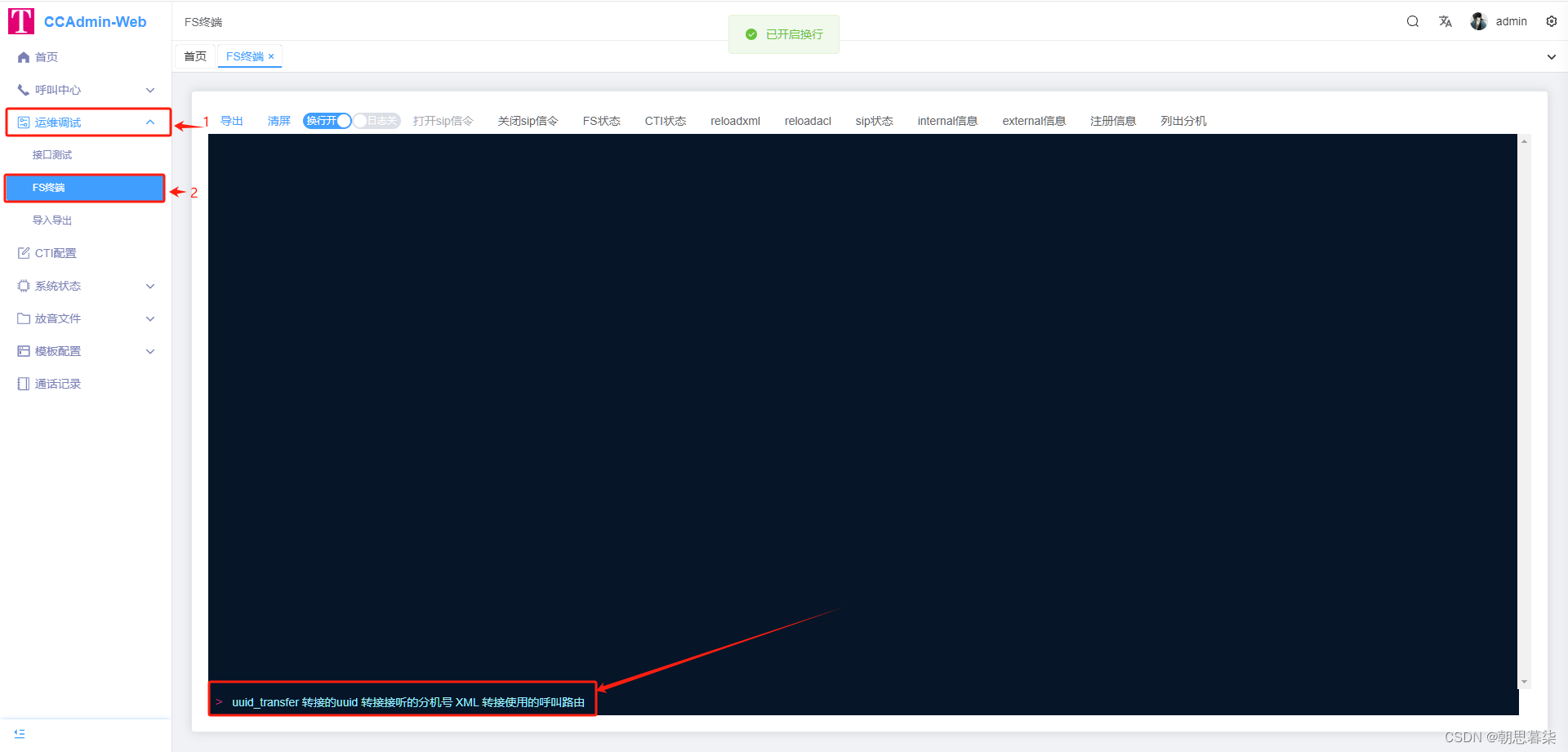
顶顶通呼叫中心中间件-如何使处于机器人话术中的通话手动转接到坐席分机上讲解(mod_cti基于FreeSWITCH)
顶顶通呼叫中心中间件使用httpapi实现电话转接操作过程讲解(mod_cti基于FreeSWITCH) 需要了解呼叫中心中间件可以点以下链接了解顶顶通小孙 1、使用httpapi接口转接 一、打开web版的ccadmin并且找到接口测试 打开web-ccadmin并且登录,登录完成之后点击运维调试-再…...
HarmonyOS—使用数据模型和连接器
Serverless低代码开发平台是一个可视化的平台, 打通了HarmonyOS云侧与端侧能力,能够轻松实现HMS Core、AGC Serverless能力调用。其中,数据模型和连接器是两大主要元素。开发者在使用DevEco Studio的低代码功能进行开发时,可以使用…...
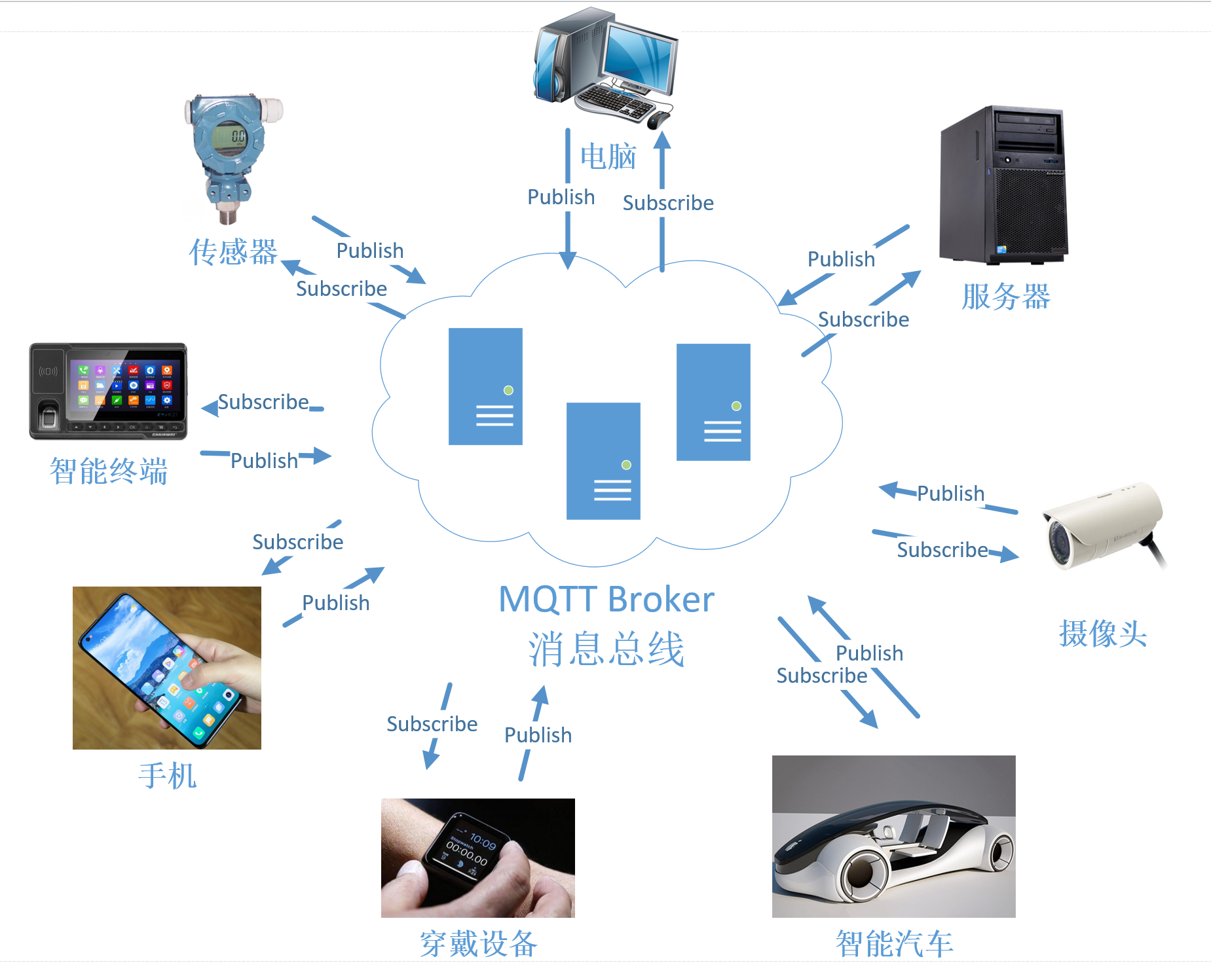
基于MQTT协议实现微服务架构事件总线
一、场景描述 昨天在博客《客户端订阅服务端事件的实现方法》中提出了利用websocket、服务端EventEmitter和客户端mitt实现客户端订阅服务端事件,大大简化了客户端对服务端数据实时响应的逻辑。上述方案适用于单服务节点的情形。 对于由服务集群支撑的微服务架构&…...
免费的Git图形界面工具sourceTree介绍
阅读本文同时请参阅-----代码库管理工具Git介绍 sourceTree是一款免费的Git图形界面工具,它简化了Git的使用过程,使得开发者可以更加方便地下载代码、更新代码、提交代码和处理冲突。下面我将详细介绍如何使用sourceTree进行这些操作。 1.下载和…...
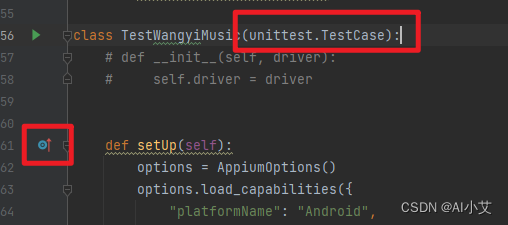
【Appium UI自动化】pytest运行常见错误解决办法
通过Appium工具录制代码在pycharm上运行报错: 错误一: 1.提示 setup() 方法运行 error failed 解决办法:未创建 init __ 方法,创建一个空的__init.py文件就解决了。 原因: 错误二: 2.运行代码ÿ…...
IDEA如何开启Dashboard
普通的面板 Run Dashboard面板 修改配置文件 找到项目的.idea文件夹 点击编辑workspace.xml文件 添加下方代码 <component name"RunDashboard"><option name"ruleStates"><list><RuleState><option name"name" valu…...

【论文复现】——一种新的鲁棒三维点云平面拟合方法
目录 一、算法原理1、论文概述2、参考文献二、代码实现三、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的GPT爬虫。 一、算法原理 1、论文概述 针对三维点云中的异常值和粗差点对平面拟合精度产生的影响,文章提出一…...
【C语言】学生宿舍信息管理系统
目录 项目说明 1. 数据结构设计 2. 功能实现 3. 主菜单设计 4. 文件操作 5. 系统使用 项目展示 1.主菜单功能界面 编辑 2.添加信息 3.查询信息 4.修改信息 5.删除信息 6.退出程序 项目完整代码 结语 在这篇博客中,我们将探讨如何使用C语言来开发…...

用Python插入页码到PDF文档
页码是许多类型文件中的重要内容,它能方便读者在文档中的导航。在创建PDF文档时,添加页码对于组织和引用内容特别有用。在本文中,我们将探讨如何利用Python程序高效地插入页码到PDF文档中,简化工作流程并创建出精美、结构合理的PD…...

LabVIEW光偏振态转换及检测仿真系统
LabVIEW光偏振态转换及检测仿真系统 随着光学技术的发展,光偏振态的研究与应用越来越广泛。为了深入理解光的偏振现象,开发了一套基于LabVIEW的光偏振态转换及检测仿真系统。该系统不仅能够模拟线偏振光、圆偏振光、椭圆偏振光等不同偏振态的产生与转换…...

scp 本地机和远程机传输文件的方法
在本地机器上,通过ssh连接到远程机器,如果想要在两个机器之间互相传输文件,那么可以使用scp。 scp运行的地方:本地机的终端 样例: 1 将本地文件filename1传输到远程主机的/home/username/filename2目录下 scp -r D:\…...
自定义神经网络二之模型训练推理
文章目录 前言模型概念模型是什么?模型参数有哪些神经网络参数案例 为什么要生成模型模型的大小什么是大模型 模型的训练和推理模型训练训练概念训练过程训练过程中的一些概念 模型推理推理概念推理过程 总结 前言 自定义神经网络一之Tensor和神经网络 通过上一篇…...
)
Java设计模式:单例模式之六种实现方式详解(二)
在Java中,单例模式是一种常见的设计模式,用于确保一个类只有一个实例,并提供一个全局访问点来获取该实例。单例模式在多种场景下都很有用,比如配置文件的读取、数据库连接池、线程池等。本文将详细介绍Java中实现单例模式的六种方…...
开创5G无线新应用:笙科电子5.8GHz 射频芯片
笙科电子(AMICCOM) 5.8GHz A5133射频芯片是一款专门设计用于在5.8GHz频率范围内(5725MHz - 5850MHz)进行射频信号处理的集成电路。这些集成电路通常包括各种功能模块,如射频前端、混合器、功率放大器、局部振荡器等,以支持无线通信系统的各种…...
使用 JMeter 生成测试数据对 MySQL 进行压力测试
博主历时三年精心创作的《大数据平台架构与原型实现:数据中台建设实战》一书现已由知名IT图书品牌电子工业出版社博文视点出版发行,点击《重磅推荐:建大数据平台太难了!给我发个工程原型吧!》了解图书详情,…...

C# cass10 面积计算
运行环境Visual Studio 2022 c# cad2016 cass10 通过面积计算得到扩展数据,宗地面积 ,房屋占地面积,房屋使用面积 一、主要步骤 获取当前AutoCAD应用中的活动文档、数据库和编辑器对象。创建一个选择过滤器,限制用户只能选择&q…...

中间件-Nginx漏洞整改(限制IP访问隐藏nginx版本信息)
中间件-Nginx漏洞整改(限制IP访问&隐藏nginx版本信息) 一、限制IP访问1.1 配置Nginx的ACL1.2 重载Nginx配置1.3 验证结果 二、隐藏nginx版本信息2.1 打开Nginx配置文件2.2 隐藏Nginx版本信息2.3 保存并重新加载Nginx配置2.4 验证结果2.5 验证隐藏版本…...
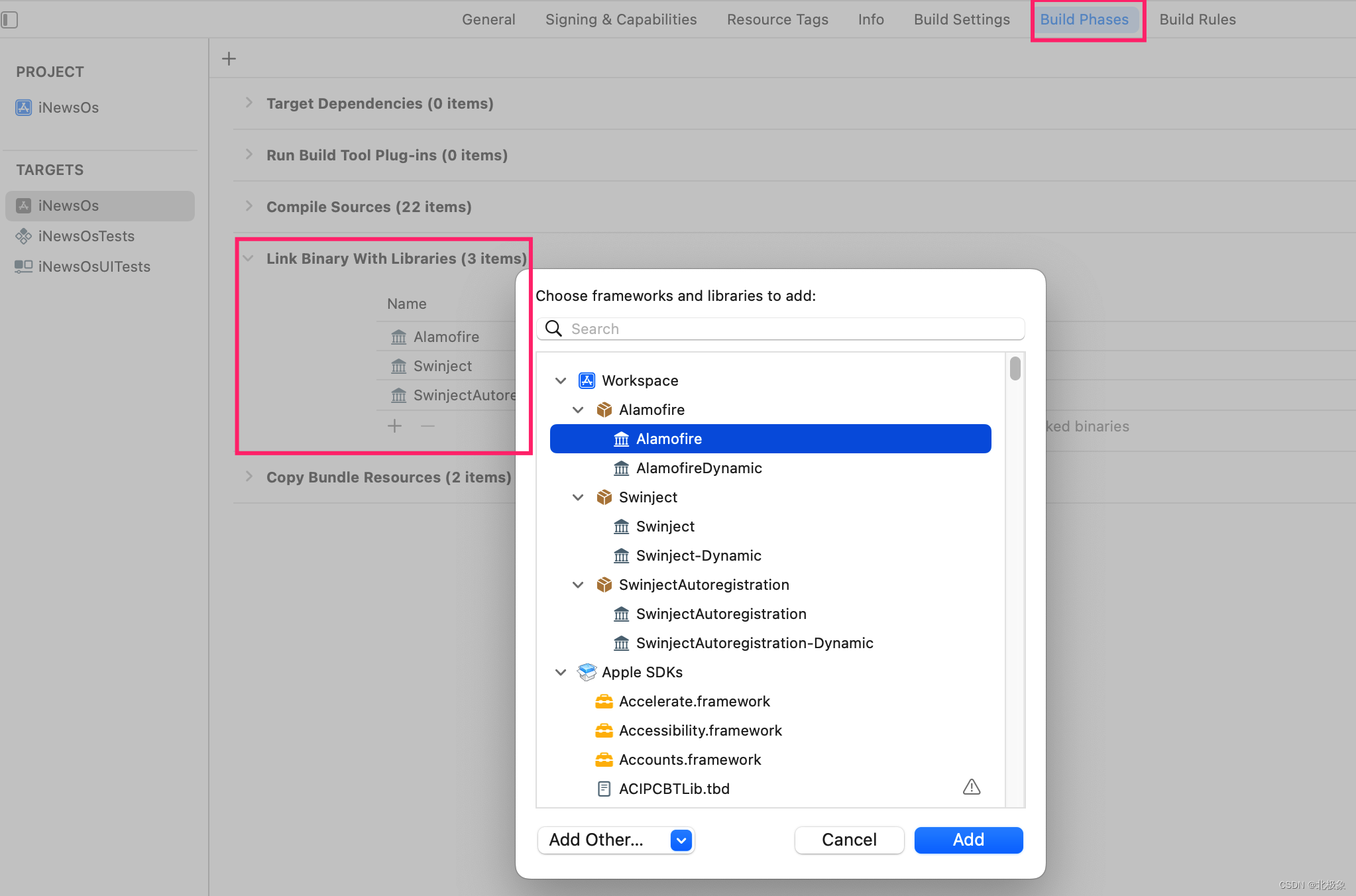
Xcode与Swift开发小记
文章目录 引子Xcode工程结构核心概念Swift语法速记(TODO)小技巧单元测试中使用awaitSwiftUI中使用ListView中取数据 常见问题Xcode添加package时连接github超时Xcode无法修改快捷键,一闪而过 引子 鉴于React Native目前版本在iOS上开发遇到诸多问题,本以…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

.Net Framework 4/C# 面向对象编程进阶
一、继承 (一)使用继承 子类可以继承父类原有的属性和方法,也可以增加原来父类不具备的属性和方法,或者直接重写父类中的某些方法。 C# 中使用“:”来表示两个类的继承。子类不能访问父类的私有成员,但是可以访问其公有成员,即只要使用 public 声明类成员,就既可以让一…...

HarmonyOS-ArkUI 自定义弹窗
自定义弹窗 自定义弹窗是界面开发中最为常用的一种弹窗写法。在自定义弹窗中, 布局样式完全由您决定,非常灵活。通常会被封装成工具类,以使得APP中所有弹窗具备相同的设计风格。 自定义弹窗具备的能力有 打开弹窗自定义布局,以…...
