图论-算法题
797. 所有可能的路径
题目:
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序)
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
示例 1:

输入:graph = [[1,2],[3],[3],[]]
输出:[[0,1,3],[0,2,3]]
解释:有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3
示例 2:

输入:graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出:[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
答案
class Solution {List<List<Integer>> res;List<Integer> list;public List<List<Integer>> allPathsSourceTarget(int[][] graph) {res = new ArrayList();list = new LinkedList();list.add(0);deal(graph,0);return res;}//回溯:深度优先遍历void deal(int[][] graph,int node){if(node==graph.length-1){res.add(new ArrayList(list));}for(int num : graph[node]){list.add(num);deal(graph,num);list.removeLast();}}
}
200. 岛屿数量
题目
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
输出:3
答案
class Solution {int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};int m,n;public int numIslands(char[][] grid) {m = grid.length;n = grid[0].length;int res = 0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]=='1'){res++;deal(grid,i,j);//将遍历过的陆地—>水}}}return res;}void deal(char[][] grid,int i,int j){if(i<0 || i>=m || j<0 || j>=n || grid[i][j]=='0'){return;}grid[i][j] = '0';for(int[] dir : dirs){deal(grid,i+dir[0],j+dir[1]);}}
}
695. 岛屿的最大面积
题目
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
示例 1:

输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
答案
class Solution {int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};int m,n;int count;public int maxAreaOfIsland(int[][] grid) {m = grid.length;n = grid[0].length;int res = 0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1){count = 0;deal(grid,i,j);res = Math.max(res,count);}}}return res;}void deal(int[][] grid,int i,int j){if(i<0 || i>=m || j<0 || j>=n || grid[i][j]==0){return;}grid[i][j] = 0;count++;for(int[] dir : dirs){deal(grid,i+dir[0],j+dir[1]);}}
}
1020. 飞地的数量
题目
给你一个大小为 m x n 的二进制矩阵 grid ,其中 0 表示一个海洋单元格、1 表示一个陆地单元格。
一次 移动 是指从一个陆地单元格走到另一个相邻(上、下、左、右)的陆地单元格或跨过 grid 的边界。
返回网格中 无法 在任意次数的移动中 离开网格边界的陆地单元格的数量。
示例 1:

输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出:3
解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
示例 2:

输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出:0
解释:所有 1 都在边界上或可以到达边界。
答案
class Solution {int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};int m,n;public int numEnclaves(int[][] grid) {m = grid.length;n = grid[0].length;for(int i=0;i<m;i++){deal(grid,i,0);deal(grid,i,n-1);}for(int j=0;j<n;j++){deal(grid,0,j);deal(grid,m-1,j);}int res = 0;for(int i=1;i<m-1;i++){for(int j=1;j<n-1;j++){if(grid[i][j]==1){res++;}}}return res;}void deal(int[][] grid,int i,int j){if(i<0 || i>=m || j<0 || j>=n || grid[i][j]==0){return;}grid[i][j] = 0;for(int[] dir : dirs){deal(grid,i+dir[0],j+dir[1]);}}
}
130. 被围绕的区域
题目
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:

输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
答案
class Solution {int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};int m,n;public void solve(char[][] board) {m = board.length;n = board[0].length;for(int i=0;i<m;i++){deal(board,i,0);deal(board,i,n-1);}for(int j=0;j<n;j++){deal(board,0,j);deal(board,m-1,j);}for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(board[i][j]=='A'){board[i][j] = 'O';}else if(board[i][j]=='O'){board[i][j] ='X';}}}}void deal(char[][] board,int i,int j){if(i<0 || i>=m || j<0 || j>=n || board[i][j]!='O'){return;}board[i][j] = 'A';for(int[] dir : dirs){deal(board,i+dir[0],j+dir[1]);}}
}
841. 钥匙和房间
题目
有 n 个房间,房间按从 0 到 n - 1 编号。最初,除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而,你不能在没有获得钥匙的时候进入锁住的房间。
当你进入一个房间,你可能会在里面找到一套不同的钥匙,每把钥匙上都有对应的房间号,即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。
给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入 所有 房间返回 true,否则返回 false。
示例 1:
输入:rooms = [[1],[2],[3],[]]
输出:true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
示例 2:
输入:rooms = [[1,3],[3,0,1],[2],[0]]
输出:false
解释:我们不能进入 2 号房间。
答案
class Solution {public boolean canVisitAllRooms(List<List<Integer>> rooms) {boolean[] visited = new boolean[rooms.size()];Queue<Integer> queue = new LinkedList();queue.offer(0);visited[0] = true;//注意这个while(!queue.isEmpty()){int curr = queue.poll();for(int index : rooms.get(curr)){if(!visited[index]){visited[index] = true;queue.offer(index);}}}for(boolean flag : visited){if(!flag){return false;}}return true;}
}
463. 岛屿的周长
题目
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 1:

输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出:16
解释:它的周长是上面图片中的 16 个黄色的边
示例 2:
输入:grid = [[1]]
输出:4
示例 3:
输入:grid = [[1,0]]
输出:4
答案
class Solution {int[][] dirs = {{1,0},{-1,0},{0,1},{0,-1}};int m,n;public int islandPerimeter(int[][] grid) {m = grid.length;n = grid[0].length;int res = 0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){if(grid[i][j]==1){for(int[] dir : dirs){int p = i + dir[0];int q = j + dir[1];if(p<0 || p>=m || q<0 || q>=n || grid[p][q]==0){res++;}}}}}return res;}
}
相关文章:

图论-算法题
797. 所有可能的路径 题目: 给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序) graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i …...

onnx 1.16 doc学习笔记七:python API一览
onnx作为一个通用格式,很少有中文教程,因此开一篇文章对onnx 1.16文档进行翻译与进一步解释, onnx 1.16官方文档:https://onnx.ai/onnx/intro/index.html](https://onnx.ai/onnx/intro/index.html), 如果觉得有收获&am…...
LACP——链路聚合控制协议
LACP——链路聚合控制协议 什么是LACP? LACP(Link Aggregation Control Protocol,链路聚合控制协议)是一种基于IEEE802.3ad标准的实现链路动态聚合与解聚合的协议,它是链路聚合中常用的一种协议。 链路聚合组中启用了…...

终端启动jupyter notebook更换端口
一、问题描述 如果尝试在端口 8889 上启动 Jupyter Notebook 但最终启动在了 8890 端口,这通常意味着 8889 端口已经被占用。要解决这个问题,可以尝试以下几种方法来关闭占用 8889 端口的进程。 1. 查找并终止占用端口的进程 首先,需要找出…...

IT发布管理,轻松部署软件
我们带来了一项令人振奋的好消息,可有效缓解构建的质量相对劣质和发布的速度相对缓慢。 ManageEngine卓豪推出了ServiceDesk Plus MSP中的IT发布管理,配备了可视化的工作流程,这是PSA-ITSM解决方案的一部分。有了这个新功能,您可以…...

2024国际生物发酵展览会独家解读-力诺天晟科技
参展企业介绍 北京力诺天晟科技有限公司,专业致力于智能仪器仪表制造,工业自动控制系统用传感器、变送器的研发、设计、销售和服务。 公司坐落于首都北京行政副中心-通州区,下设生产子公司位于河北香河经济开发区,厂房面积 300…...

YOLOv9尝鲜测试五分钟极简配置
pip安装python包: pip install yolov9pip在https://github.com/WongKinYiu/yolov9/tree/main中下载好权重文件yolov9-c.pt。 运行下面代码: import yolov9model yolov9.load("yolov9-c.pt", device"cpu") # load pretrained or c…...
消息中间件篇之Kafka-消息不丢失
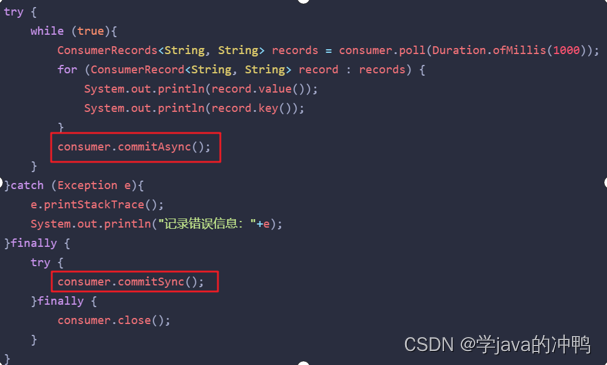
一、 正常工作流程 生产者发送消息到kafka集群,然后由集群发送到消费者。 但是可能中途会出现消息的丢失。下面是解决方案。 二、 生产者发送消息到Brocker丢失 1. 设置异步发送 //同步发送RecordMetadata recordMetadata kafkaProducer.send(record).get();//异…...

Rust使用calamine读取excel文件,Rust使用rust_xlsxwriter写入excel文件
Rust使用calamine读取已存在的test.xlsx文件全部数据,还读取指定单元格数据;Rust使用rust_xlsxwriter创建新的output.xlsx文件,并写入数据到指定单元格,然后再保存工作簿。 Cargo.toml main.rs /*rust读取excel文件*/ use cala…...
)
中文文本分类(pytorch 实现)
import torch import torch.nn as nn import torchvision from torchvision import transforms, datasets import os, PIL, pathlib, warningswarnings.filterwarnings("ignore") # 忽略警告信息# win10系统 device torch.device("cuda" if torch.cuda.i…...

【每日前端面经】2023-02-27
题目来源: 牛客 CSS盒模型 CSS中的盒子包括margin|border|padding|content四个部分,对于标准盒子模型(content-box)的widthcontent,但是对于IE盒子模型(border-box)的widthcontentborder2padding2 CSS选…...

springboot + easyRules 搭建规则引擎服务
依赖 <dependency><groupId>org.jeasy</groupId><artifactId>easy-rules-core</artifactId><version>4.0.0</version></dependency><dependency><groupId>org.jeasy</groupId><artifactId>easy-rules…...

Mac电脑配置环境变量
1.打开配置文件bash_profile open -e .bash_profile 2.如果没有创建过.bash_profile,则先需要创建 touch .bash_profile 3.输入你要配置的环境变量 #Setting PATH for Android ADB Tools export ANDROID_HOME/Users/xxx/android export PATH${PATH}:${ANDROID_HOME}…...
Windows系统x86机器安装(麒麟、统信)ARM系统详细教程
本次介绍在window系统x86机器上安装国产系统 arm 系统的详细教程。 注:ubuntu 的arm系统安装是一样的流程。 1.安装环境准备。 首先,你得有台电脑,配置别太差,至少4核8G内存,安装window10或者11都行(为啥…...

消息中间件篇之RabbitMQ-高可用机制
一、怎么保证高可用性 在生产环境下,使用集群来保证高可用性,一般我们采用普通集群、镜像集群、仲裁队列。 二、普通集群 普通集群,或者叫标准集群(classic cluster),具备下列特征: 1. 会在集…...
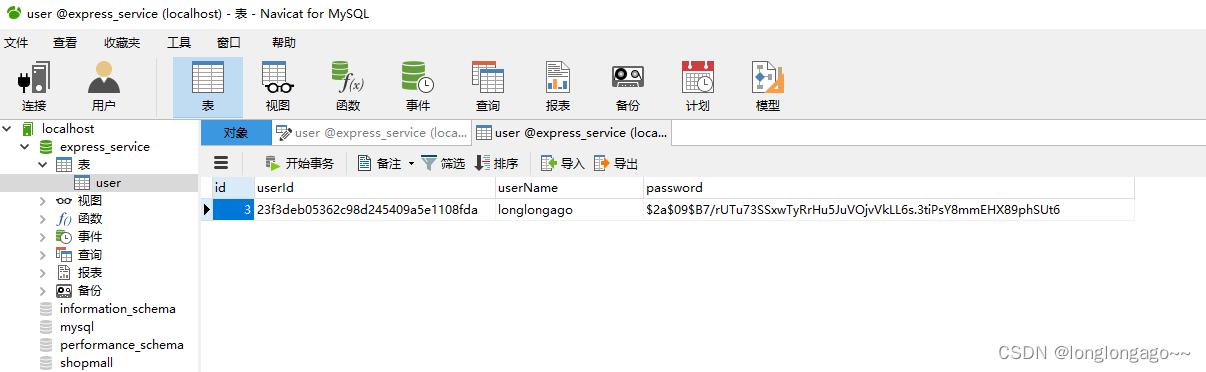
express+mysql+vue,从零搭建一个商城管理系统5--用户注册
提示:学习express,搭建管理系统 文章目录 前言一、新建user表二、安装bcryptjs、MD5、body-parser三、修改config/db.js四、新建config/bcrypt.js五、新建models文件夹和models/user.js五、index.js引入使用body-parser六、修改routes/user.js七、启动项…...

canvas水波纹效果,jquery鼠标水波纹插件
canvas水波纹效果,jquery鼠标水波纹插件 效果展示 jQuery水波纹效果,canvas水波纹插件 HTML代码片段 <div class"scroll04wrap"><h3>发展历程</h3><div class"scroll04"><p>不要回头,一…...

Zookeeper客户端命令、JAVA API、监听原理、写数据原理以及案例
1. Zookeeper节点信息 指定服务端,启动客户端命令: bin/zkCli.sh -server 服务端主机名:端口号 1)ls / 查看根节点下面的子节点 ls -s / 查看根节点下面的子节点以及根节点详细信息 其中,cZxid是创建节点的事务id,…...
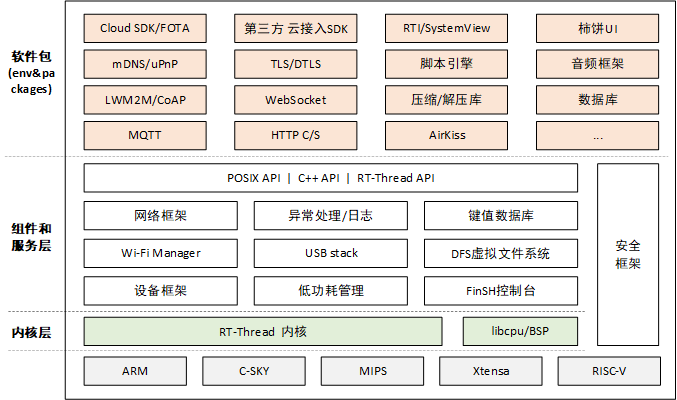
[嵌入式系统-34]:RT-Thread -19- 新手指南:RT-Thread标准版系统架构
目录 一、RT-Thread 简介 二、RT-Thread 概述 三、许可协议 四、RT-Thread 的架构 4.1 内核层: 4.2 组件与服务层: 4.3 RT-Thread 软件包: 一、RT-Thread 简介 作为一名 RTOS 的初学者,也许你对 RT-Thread 还比较陌生。然…...
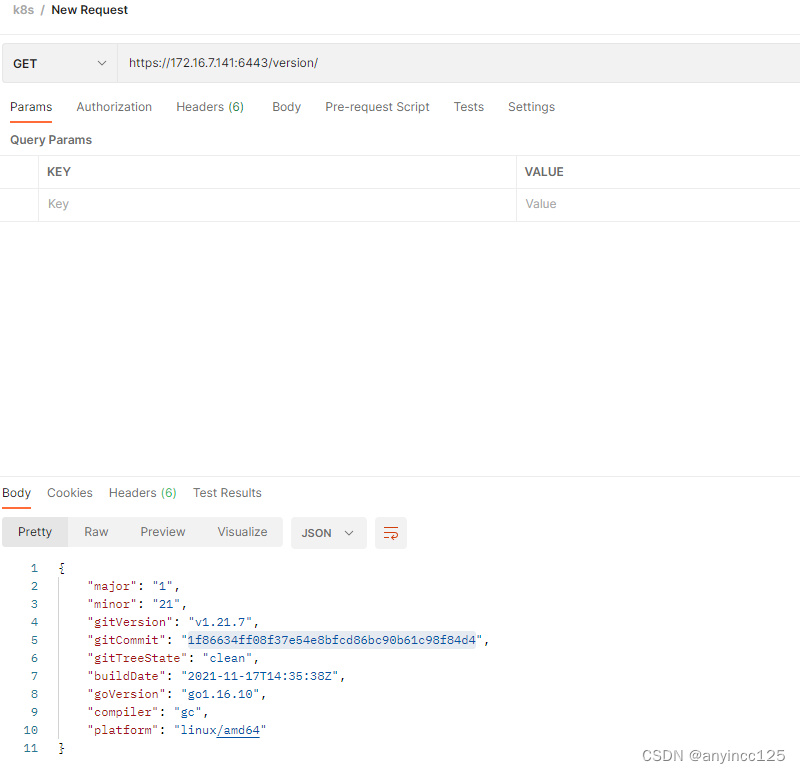
postman访问k8s api
第一种方式: kubectl -n kubesphere-system get sa kubesphere -oyaml apiVersion: v1 kind: ServiceAccount metadata:annotations:meta.helm.sh/release-name: ks-coremeta.helm.sh/release-namespace: kubesphere-systemcreationTimestamp: "2023-07-24T07…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...
