AtCoder Beginner Contest 292 (A - E) 记录第一场ABC
AtCoder Beginner Contest 292 A - E
- 前言
- Q1 A - CAPS LOCK
- Q2 Yellow and Red Card
- Q3 Four Variables
- Q4 D - Unicyclic Components
- Q5 E - Transitivity
前言
本来晚上在打Acwing周赛,最后一题Trie想不出来咋写,看群里有人说ABC要开始了,想着没打过ABC就去报了一下,感觉难度大概是cf的Div3到Div4之间吧,总共写了五个题,E题想复杂了快结束才交过。总的来说手速很重要。
Q1 A - CAPS LOCK
题意:给一个字符串,要求把小写字母改成大写。
分析: 循环模拟下就可以了,时间复杂度O(n)O(n)O(n)
void solve()
{string s;cin >> s;for(auto &c : s){if(c >= 'a' && c <= 'z') c += 'A' - 'a';}cout << s << endl;
}
Q2 Yellow and Red Card
题意:有n个人,发生过q个事件,每个事件要么是某人领黄牌/红牌/询问某人是否出局,累计获得两张黄牌或者是得到过红牌就会出局。
分析:开一个数组cnt记录即可,黄牌+1, 红牌+2. 大于等于2的就要出局了。时间复杂度O(q)O(q)O(q)
{cin >> n >> q;vector<int> cnt(n + 1);while(q--){int t, x;cin >> t >> x;if(t == 1) cnt[x] += 1;else if(t == 2) cnt[x] += 2;else cout << (cnt[x] >= 2 ? "Yes" : "No") << endl;}
}
Q3 Four Variables
题意:问四元组(A, B, C, D)满足AB + CD = n 的个数。
分析:先考虑简单的问题,如果问X + Y = n,求(X, Y)的数量,答案显然。然后再考虑怎么凑成X,就是X的因子对的数量,Y也是同理。设f[x]f[x]f[x]表示x的因子对数量,那么答案就是f[1]∗f[n−1]+f[2]∗f[n−2]+...+f[n−1]∗f[1]。f[1] * f[n - 1] + f[2] * f[n - 2] + ... + f[n - 1] * f[1]。f[1]∗f[n−1]+f[2]∗f[n−2]+...+f[n−1]∗f[1]。 时间复杂度O(nn)O(n\sqrt{n})O(nn)
#define int long long
void solve()
{cin >> n;vector<int> f(n + 1);for(int i = 1; i <= n; ++i){int t = i;for(int j = 1; j <= t / j; ++j)if(t % j == 0) f[i] += 1 + (j != t / j);}int ans = 0;for(int i = 1; i <= n; ++i){int j = n - i;ans += f[i] * f[j];}cout << ans << endl;
}
Q4 D - Unicyclic Components
题意:给一张有向图图,询问是否每个连通分量内点的数量都等于边的数量。
分析:据说分别维护点和边的并查集和集合内元素数量的做法可以过,貌似官方给的题解也是这么做的,但是我写的是维护连通块内环的个数。把题目给出的有向图当作无向图,什么时候连通分量里面的点的数量会等于边的数量呢?设点数为xxx, 边数为yyy.如果连通分量内无环,因为各点都连通,所以y=x−1y = x - 1y=x−1。可以发现如果要让x==yx == yx==y, 需要在原图上补充一条边,因为原图已经连通,加上的这条边一定会增添一个环。用cntcntcnt维护并查集集合内环数量,合并a,ba, ba,b的时候,如果a,ba, ba,b之前不在一个集合内,那么他们环的数量相加(因为此前这两个连通分量并不连通,所以环数量直接相加即可)。如果a, b之前已经在一个集合,那么这个集合的环数量+1. 最后判断每个集合的环数量是否恰好等于1.时间复杂度O(n)O(n)O(n)
/** @Author: gorsonpy* @Date: 2023-03-04 20:21:52* @LastEditors: gorsonpy* @LastEditTime: 2023-03-04 20:26:28* @FilePath: \vscode-c\D_-_Unicyclic_Components.cpp* @Description: */
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5 + 10;int p[N], cnt[N];
int n, m;int find(int x)
{if(x != p[x]) p[x] = find(p[x]);return p[x];
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; ++i) p[i] = i, cnt[i] = 0;while(m--){int a, b;cin >> a >> b;int pa = find(a), pb = find(b);if(pa != pb) p[pa] = pb, cnt[pb] += cnt[pa];else ++cnt[pb];}bool ok = true;for(int i = 1; i <= n; ++i)if(p[i] == i){if(cnt[i] != 1) ok = false;}cout << (ok ? "Yes" : "No") << endl;return 0;
}
Q5 E - Transitivity
写完D看了一下群,有人说E是搜索。。当时就紧张了因为不太会写搜索,导致把题目想歪了。。其实不用搜索也可以做的,比赛后一个小时都在写E,不过F那个几何去想应该也做不出来吧(
题意:给定一张有向图,每次操作可以加一条边,问最少操作次数,使得对于整张图,若存在a到b的边,存在b到c的边,那么一定也有a到c的边。
分析:注意到数据规模并不大,只有2000点,2000边。考虑一下暴力做法。实际上,只需要开数组记录对于每个点, 进入他的点集合in, 和他出去的out。 然后循环所有的点i,看每个(x, y)是否有x到y的边,x是进入i的一个点,y是i出去的一个点。如果没边加上就行了,答案加1, 就这么简单。但是可能会想,为什么做一次就可以了?会不会存在比如说第一次加的边引起后续反应了,导致还要再加一轮边?实际上并不会。因为本题除了暴力还有一个性质:在最终的图中,x所直接连的点一定是在原始的图中x所能抵达的点(不一定是直接相连)。反之亦然。这个用归纳法是显然的,因为每次我们添加边(x, y)的时候并没有改变x ->y的可达性。所以这个做法实际上等价于搜索,也就是找原图中点i所能抵达的点p,然后计算i到p路径上的边数量,最后减去原图已有的边。 时间复杂度O(nm)O(nm)O(nm)
#define pb push_back
int g[N][N];
void solve()
{cin >> n >> m;vector<vector<int>> in(n + 1), out(n + 1);while(m--){int x, y;cin >> x >> y;out[x].pb(y);in[y].pb(x);g[x][y] ++;}int ans = 0;for(int i = 1; i <= n; ++i){auto din = in[i], dout = out[i];for(auto x : din)for(auto y : dout){if(x == y) continue;if(!g[x][y]) {++ans;g[x][y] ++;in[y].pb(x);out[x].pb(y);}}}cout << ans << endl;
}相关文章:
 记录第一场ABC)
AtCoder Beginner Contest 292 (A - E) 记录第一场ABC
AtCoder Beginner Contest 292 A - E前言Q1 A - CAPS LOCKQ2 Yellow and Red CardQ3 Four VariablesQ4 D - Unicyclic ComponentsQ5 E - Transitivity前言 本来晚上在打Acwing周赛,最后一题Trie想不出来咋写,看群里有人说ABC要开始了,想着没…...
ubuntu安装使用putty
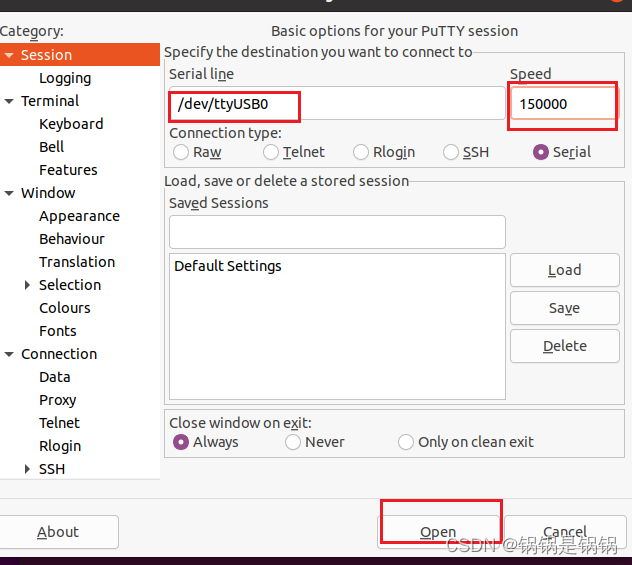
一、安装 安装虚拟机串口 sudo apt-get install putty sudo apt install -y setserial 二、使用 虚拟机连接串口 sudo setserial -g /dev/ttyS* 查看硬件对应串口 找到不是unknown的串口 sudo putty...

【CS144】Lab5与Lab6总结
Lab5与Lab6Lab汇总Lab5概述Lab6概述由于Lab5和Lab6相对比较简单(跟着文档一步一步写就行),于是放在一起做一个简单概述(主要是懒得写了…) Lab汇总 Lab5概述 lab5要求实现一个IP与Ethernet(以太网&#x…...

GDScript 导出变量 (Godot4.0)
概述 导出变量的功能在3.x版本中也是有的,但是4.0版本对其进行了语法上的改进。 导出变量在日常的游戏制作中提供节点的自定义参数化调节功能时非常有用,除此之外还用于自定义资源。 本文是(Bilibili巽星石)在4.0官方文档《GDScr…...
shell:#!/usr/bin/env python作用是什么
我们经常会在别人的脚本文件里看到第一行是下面这样 #!/usr/bin/python或者 #!/usr/bin/env python 那么他们有什么用呢? 要理解它,得把这一行语句拆成两部分。 第一部分是 #! 第二部分是 /usr/bin/python 或者 /usr/bin/env python 关于 #! 这个…...

计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架
报告下载: 计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架 简介 “AI算力时代已经来临,计算机行业正在经历着一场前所未有的变革!” 这是一个充满活力和兴奋的时代,人工智能(AI)已…...
『MyBatis技术内幕』源码调试前提
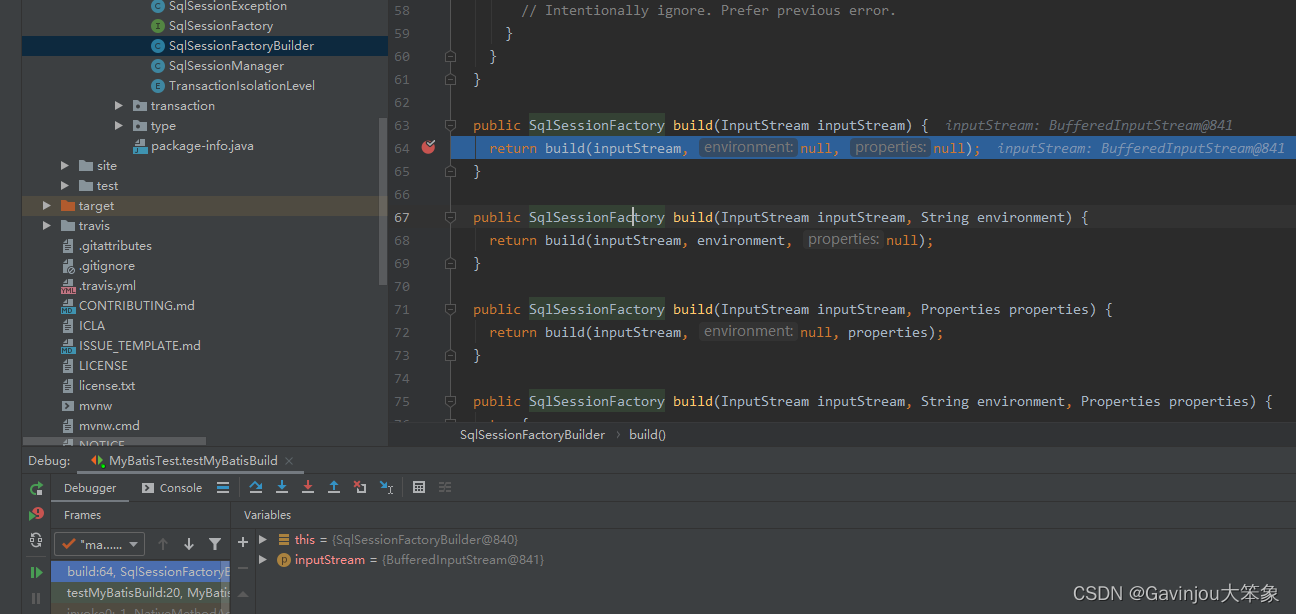
准备源代码包 下载源代码 3.4.6 版本 https://github.com/mybatis/mybatis-3/releases?page2 通过 idea 导入然后回自动下载所有依赖,根据 3.4.6 版本的 pom.xml 找到依赖的 mybatis-parent 版本 <parent><groupId>org.mybatis</groupId><ar…...

# Linux最新2022年面试题大汇总,附答案
# Linux最新2022年面试题大汇总,附答案 ### [1、cp(copy单词缩写,复制功能)](最新2021年面试题大汇总,附答案.md#1cpcopy单词缩写复制功能) cp /opt/java/java.log /opt/logs/ ;把java.log 复制到/opt/logs/下 cp /…...

css中重难点整理
一、vertical-align 在学习vertical-align的时候,可能会很困惑。即使网上有一大推文章讲veitical-align,感觉看完好像懂了,等自己布局的时候用到vertical-align的时候好像对它又很陌生。这就是我在布局的时候遇到的问题。 本来vertical-align就很不好理…...

JavaScript-扫盲
文章目录1. 前言2. 第一个 JavaScript 程序3. javaScript 的基础语法3.1 变量3.2 数据类型3.3 运算符3.4 条件语句3.5 数组3.6 函数3.7 作用域3.8 对象4. WebAPI4.1 DOM 基本概念4.2 常用 DOM API4.3 事件4.4 操作元素4.5 网页版猜数字游戏4.6 留言版1. 前言 提问 java 和 java…...
bpftrace 笔记
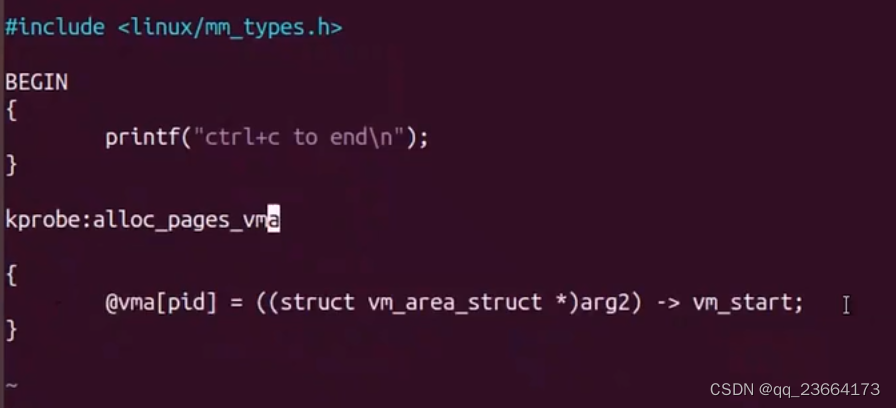
bpftrace -e BEFIN {printf("hello world!\n");}获取调用 vfs_read 函数的进程id, 每2s打印一次 bpftrace -e kprobe:vfs_read {ID pid;} interval:s:2 {printf{"ID:%d\n", ID);}用户态调试 bpftrace -e uprobe:/*/a.out:and {printf("ID:%d\n&qu…...
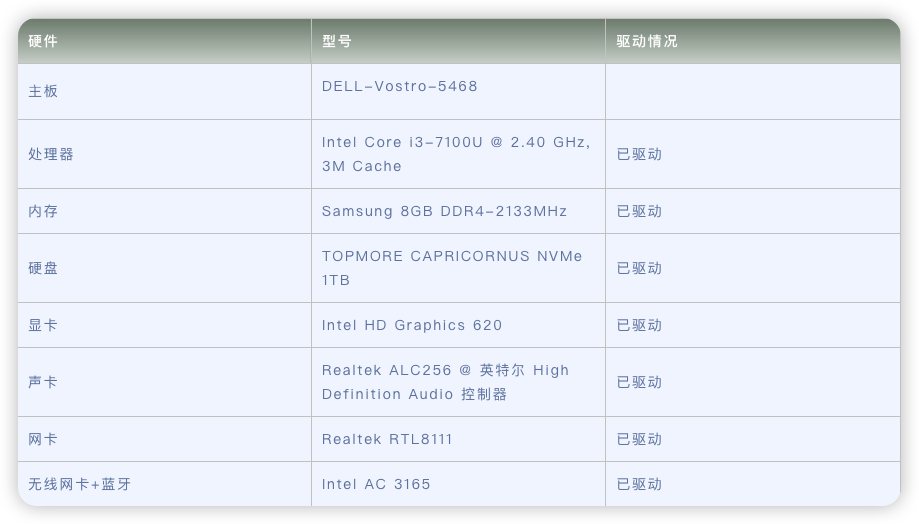
DELL-Vostro-5468电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板DELL-Vostro-5468处理器Intel Core i3-7100U 2.40 GHz, 3M Cache已驱动内存Samsung 8GB DDR4-2133MHz已驱动硬盘TOPMORE CAPRICORNUS NVMe 1TB已驱动显卡Intel HD Graphics 620已驱动声卡Realtek ALC2…...

阶段二11_面向对象高级_学生管理系统案例2
主要内容: 添加学生 static关键字一.添加学生时判断id是否存在 0.思路图片: 04/图片/2_添加学生判断id存在的问题分析.png 1.思路实现详细步骤: StudentController【客服接待】 /** 接收到学生id后,判断该id在数组中是否存在 这…...
spring源码篇(3)——bean的加载和创建
spring-framework 版本:v5.3.19 文章目录bean的加载bean的创建总结getBean流程createBean流程doCreateBean流程bean的加载 beanFactory的genBean最常用的一个实现就是AbstractBeanFactory.getBean()。 以ApplicationContext为例,流程是: ApplicationCon…...

Spring 中事务的传播级别
Spring 中事务的传播级别 REQUIRED(默认):默认的隔离级别,如果当前存在一个事务,就加入该事务,如果当前没有事务,就创建一个新的事务。 REQUIRED_NEW:不管当前是否存在事务,都创建一个新的事物…...

ECharts可视化库--常用组件
目录 一.series系列 二.常见组件 1.标题title 2.图例legend 3.工具栏toolbox 4.提示框tooltip 5.坐标轴 xAxis yAsix 6.series系列 上一篇已经介绍了ECharts库的导入工作和绘制基本的图标,今天我们来了解一下常用的组件,如果对数据可视化感兴…...
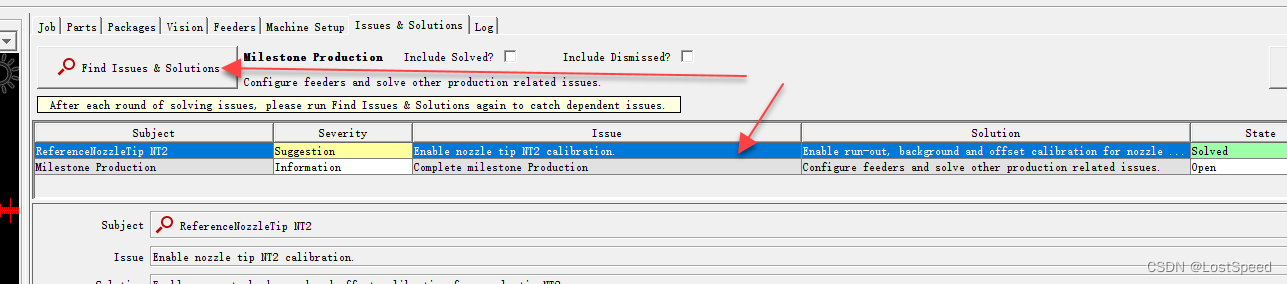
openpnp - 设备开机后, 吸嘴校验失败的解决方法
文章目录openpnp - 设备开机后, 吸嘴校验失败的解决方法概述重新校验吸嘴ENDopenpnp - 设备开机后, 吸嘴校验失败的解决方法 概述 设备开机后, 默认会校验吸嘴座上已经安装的2个吸嘴. 如果开机校验吸嘴失败, 就需要用向导重新校验失败的吸嘴. 具体是哪个吸嘴校验失败, 可以看…...
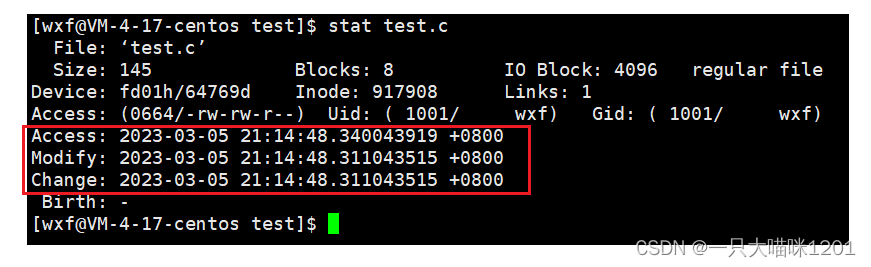
【Linux学习】基础IO——软硬链接 | 制作动静态库
🐱作者:一只大喵咪1201 🐱专栏:《Linux学习》 🔥格言:你只管努力,剩下的交给时间! 基础IO🍓软硬链接🌲软链接🌲硬链接🍓动静态库&…...
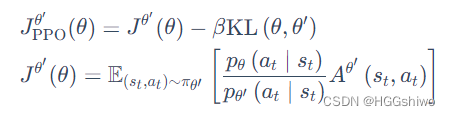
如何分辨on-policy和off-policy
on-policy的定义:behavior policy和target-policy相同的是on-policy,不同的是off-policy。 behavior policy:采样数据的策略,影响的是采样出来s,a的分布。 target policy:就是被不断迭代修改的策略。 如果是基于深度…...

第三讲:ambari编译后的安装包制作流程说明
一、概述 前两讲,我们已经将 Ambari 源码编译成功。现在我们想将 Ambari 编译后的 rpm 包,都放到 yum 本地仓库中,这样 Ambari 与 HDP 在安装部署时,就直接使用的我们自己编译的安装包了。 Ambari 的 rpm 包,有这么几类: ambari-server rpmambari-agent rpmambari metr…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
