Offer必备算法09_分治快排_四道力扣OJ(快排三路划分)
目录
分治快排算法原理
①力扣75. 颜色分类
解析代码
②力扣912. 排序数组
解析代码
③力扣215. 数组中的第K个最大元素
解析代码
④力扣LCR 159. 库存管理 III(剑指 Offer . 最小的k个数)
解析代码
本篇完。
分治快排算法原理
分治就是分而治之,快排在数据结构也学过了,现在来学一学三路划分快排(数组划分三块):
前面我们已经实现了三个版本的快速排序的算法,分别是hoare法,挖坑法和前后指针法。但是前面的三个版本的快速排序在某些极端场景中效率都会变得很低,例如大部分都是同一个数的时候,前面的三种方法都不能很高效地完成排序,时间复杂度退化成了O(N^2),所以有必要对之前的排序方法进行一些改进,使它能够适应包含任何数据的数组。于是就有大佬想出了一个更牛的方法,那就是三路划分快排。
三路划分快排的思路:三路划分,顾名思义就是把数组分成三个部分进行排序,在待排序数组中随机选定一个key,把数组分成小于key的,等于key的,还有大于key的。
具体操作是:
- 定义一个left下标为数组首元素下标的前一个位置,即left=begin-1;
- 再定义一个right下标为数组最后一个元素的下标的后一个位置,即right=end+1;
- 再定义一个下标cur=left,作为遍历数组的下标,一共就left,cur,right三个下标。
- 从a[cur]开始与key比较,如果a[cur]<key,就用a[cur]和a[++left]交换(记住这里是先++,后交换),然后++cur;如果a[cur]>key,就用a[cur]和a[- -right]交换(记住这里是先减减,后交换);如果a[cur]==key,那就只++cur即可,
- 这样循环往复,直到cur=right就结束,最后得到的a[begin,left]是比key小的数,a[left+1,right-1]是等于key的数,a[right,end]是大于key的数,划分成三路之后,中间这一路就不用再进行排序了,因为中间这一路都是等于key的,所以已经有序了,只需要对左路和右路再进行递归排序即可。
①力扣75. 颜色分类
75. 颜色分类
难度 中等
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库内置的 sort 函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0] 输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1] 输出:[0,1,2]
提示:
n == nums.length1 <= n <= 300nums[i]为0、1或2
进阶:
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
class Solution {
public:void sortColors(vector<int>& nums) {}
};解析代码
数组分三块:三指针思想:left i right,
0 到 left 全是 0,right 到 i 全是 1,i 到 right 全是未处理的元素,right到nums.size();全是2。
class Solution {
public:void sortColors(vector<int>& nums) {int left = -1, i = 0, right = nums.size();while(i < right){if(nums[i] == 0)swap(nums[++left], nums[i++]);else if(nums[i] == 1)++i;else // == 2swap(nums[--right], nums[i]);}}
};②力扣912. 排序数组
912. 排序数组
难度 中等
给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
提示:
1 <= nums.length <= 5 * 10^4-5 * 10^4 <= nums[i] <= 5 * 10^4
class Solution {
public:vector<int> sortArray(vector<int>& nums) {};解析代码
又是这题,C语言用八大排序测试过了,现在再加三指针的快排:
随机选key在《算法导论》里被用概率论证明了最能让快排接近O(N*logN),而且下面的三路划分可以让快排最慢的情况:排序重复元素O(N^2),直接优化成O(N),因为遍历一次就已经全都分到三部分中等于key的部分了。
class Solution {
public:vector<int> sortArray(vector<int>& nums) {srand(time(nullptr)); // 随机数种子qsort(nums, 0, nums.size() - 1);return nums;}void qsort(vector<int>& nums, int begin, int end){if(begin >= end)return;int key = nums[rand() % (end - begin + 1) + begin]; // 随机选key// rand() % (r - l + 1)是[0, n-1] 再加偏移量begin就是要排序的区间int i = begin, left = begin - 1, right = end + 1;while(i < right){if(nums[i] < key)swap(nums[++left], nums[i++]);else if(nums[i] == key)++i;else // >keyswap(nums[--right], nums[i]);}// [begin, left] [left + 1, right - 1] [right, end]qsort(nums, begin, left);qsort(nums, right, end);}
};③力扣215. 数组中的第K个最大元素
215. 数组中的第K个最大元素
难度 中等
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 10^5-10^4 <= nums[i] <= 10^4
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {}
};解析代码
TopK问题,用堆排思路写过,时间复杂度是O(N*logN),现在用三路划分的快排思想写一下,时间复杂度是O(N),《算法导论》里有两页的证明。
思路:在快排中,当我们把数组「分成三块」之后: [begin, left] [left + 1, right - 1] [right, end] ,我们可以通过计算每一个区间内元素的个数,进而推断出最小的 k 个数在哪些区间里面。那么我们可以直接去相应的区间继续划分数组即可。
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {srand(time(nullptr));return qsort_topk(nums, 0, nums.size() - 1, k);}int qsort_topk(vector<int>& nums, int begin, int end, int k){ // 到begin和end区间找第k大元素if(begin == end)return nums[begin];int key = nums[rand() % (end - begin + 1) + begin];int i = begin, left = begin - 1, right = end + 1;while(i < right){if(nums[i] < key)swap(nums[++left], nums[i++]);else if(nums[i] == key)i++;elseswap(nums[--right], nums[i]);}// [begin, left] [left+1, right-1] [rignt, end]int c = end - right + 1; // 右区间元素个数int b = right - left - 1; // 中间区间元素个数if(c >= k) // 右区间元素个数>=k,到右区间找return qsort_topk(nums, right, end, k);else if(b + c >= k) // 右两区间元素个数>=k,返回中间区间元素return key;else // 到左区间找第k-b-c大的return qsort_topk(nums, begin, left, k - b - c);}
};④力扣LCR 159. 库存管理 III(剑指 Offer . 最小的k个数)
(原:剑指 Offer . 最小的k个数)
LCR 159. 库存管理 III
难度 简单
仓库管理员以数组 stock 形式记录商品库存表,其中 stock[i] 表示对应商品库存余量。请返回库存余量最少的 cnt 个商品余量,返回 顺序不限。
示例 1:
输入:stock = [2,5,7,4], cnt = 1 输出:[2]
示例 2:
输入:stock = [0,2,3,6], cnt = 2 输出:[0,2] 或 [2,0]
提示:
0 <= cnt <= stock.length <= 10000
0 <= stock[i] <= 10000
class Solution {
public:vector<int> inventoryManagement(vector<int>& stock, int cnt) {};解析代码
之前也写过了,用库里的sort排序时间是O(N*logN),用堆时间是O(N*logK),用三路划分快排思想的快速选择算法时间是O(N)。
当我们把数组分成三块之后,可以通过计算每一个区间内元素的个数,进而推断出最小的 k 个数在哪些区间里面。那么我们可以直接去相应的区间继续划分数组即可。
class Solution {
public:vector<int> inventoryManagement(vector<int>& stock, int cnt) {srand(time(nullptr));qsort_topk(stock, 0, stock.size() - 1, cnt);return {stock.begin(), stock.begin() + cnt};}void qsort_topk(vector<int>& arr, int begin, int end, int k){ // 把数组前k个小的丢到前面,不一定有序if(begin >= end)return ;int key = arr[rand() % (end - begin + 1) + begin];int i = begin, left = begin - 1, right = end + 1;while(i < right){if(arr[i] < key)swap(arr[++left], arr[i++]);else if(arr[i] == key)++i;elseswap(arr[--right], arr[i]);}// [begin, left] [left+1, right-1] [right, end]int a = left - begin + 1; // 左区间元素个数int b = right - left - 1; // 中间区间元素个数if(a > k)qsort_topk(arr, begin, left, k);else if(a + b >= k)return;else // 到第三区间找k - a - b小的qsort_topk(arr, right, end, k - a - b);}
};本篇完。
此专栏下一篇是分治归并的内容,归并排序思想刷OJ。
相关文章:
)
Offer必备算法09_分治快排_四道力扣OJ(快排三路划分)
目录 分治快排算法原理 ①力扣75. 颜色分类 解析代码 ②力扣912. 排序数组 解析代码 ③力扣215. 数组中的第K个最大元素 解析代码 ④力扣LCR 159. 库存管理 III(剑指 Offer . 最小的k个数) 解析代码 本篇完。 分治快排算法原理 分治就是分而治…...
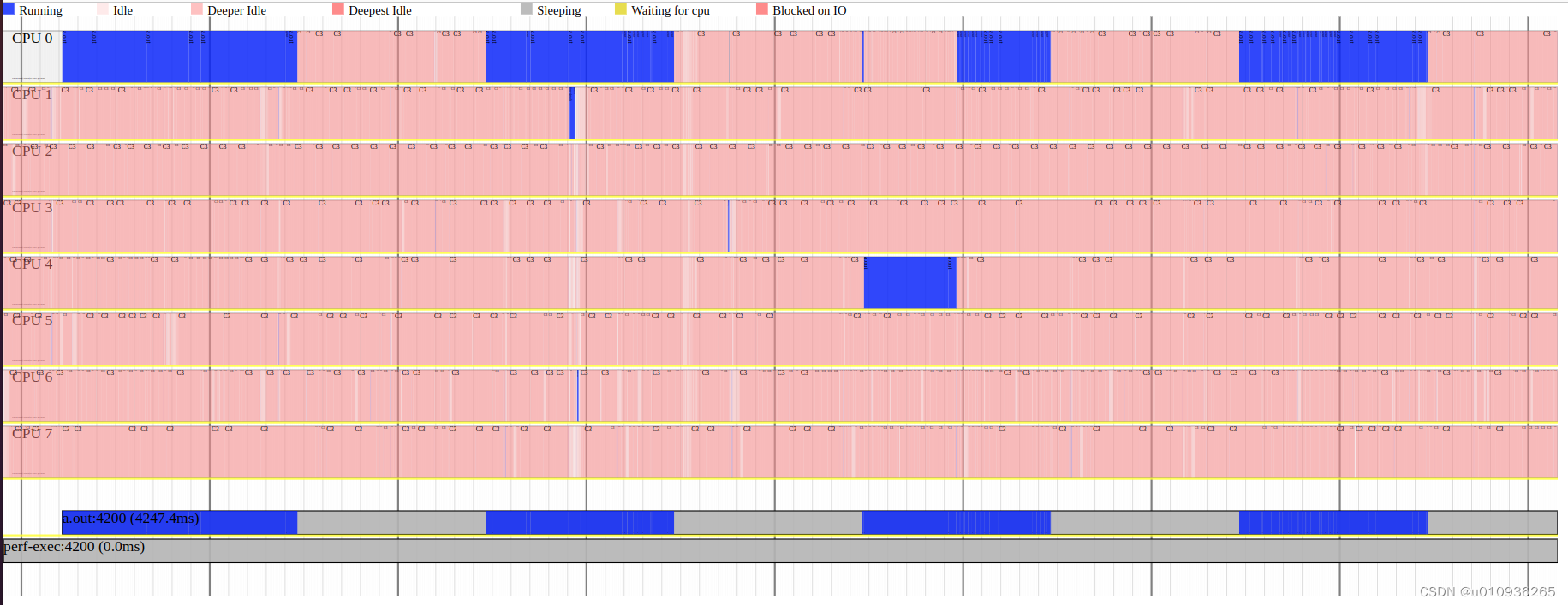
Linux下性能分析的可视化图表工具
1 sar 和sadf 1.1 简介 sar命令可以记录系统下的常见活动信息,例如CPU使用率、网络统计数据、Block I/O数据、内存使用情况 等。 sar命令的“-o [file_name]”参数可以将系统活动数据记录到file_name文件,然后通过sadf来解析,sadf命令的“-g…...

泽攸科技JS系列高精度台阶仪在半导体领域的应用
泽攸科技JS系列高精度台阶仪是一款先进的自主研发的国产台阶仪,采用了先进的扫描探针技术。通过扫描探针在样品表面上进行微观测量,台阶仪能够准确获取表面形貌信息。其工作原理基于探针与样品表面的相互作用力,通过测量探针的微小位移&#…...

c++实现栈和队列类
c实现栈和队列类 栈(Stack)Stack示意图Stack.cpp 队列(queue)queue 示意图queue.cpp 栈(Stack) Stack示意图 Stack.cpp #pragma once #include "ListStu.cpp"template<typename T> class Stack { public: /* * void push(T& tDate)* 参数一 :…...

MySQL优化之索引下推
(/≧▽≦)/~┴┴ 嗨~我叫小奥 ✨✨✨ 👀👀👀 个人博客:小奥的博客 👍👍👍:个人CSDN ⭐️⭐️⭐️:传送门 🍹 本人24应届生一枚,技术和水平有限&am…...

【Java程序设计】【C00338】基于Springboot的银行客户管理系统(有论文)
基于Springboot的银行客户管理系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的银行客户管理系统,本系统有管理员、员工以及用户二种角色; 管理员:个人中心、管理员管理、客…...

C语言中大小写字母的转化
目录 C语言中大小写字母的转化 一、引言 二、C语言中的大小写转换函数 toupper()函数 tolower()函数 三、注意事项 四、总结 C语言中大小写字母的转化 一、引言 在C语言编程中,字符的处理是一个重要的环节。字符包括字母、数字、标点符号等,其中…...

Camunda7.18流程引擎启动出现Table ‘camunda_platform_docker.ACT_GE_PROPERTY‘的解决方案
文章目录 1、问题描述2、原因分析3、解决方案3.1、方案一:降低mysql版本3.2、方案二:增加nullCatalogMeansCurrent参数(推荐) 4、总结 1、问题描述 需要在docker中,部署Camunda流程引擎。通过启动脚本camunda-platfor…...

红队打靶:DR4G0N B4LL打靶思路详解(vulnhub)
目录 写在开头 第一步:主机发现 第二步:Web渗透 第三步:curl批量访问(无果) 第四步:Vulnhub目录发现 第五步: 图片隐写破解 第六步:ssh私钥登录 第七步:变量劫持提…...
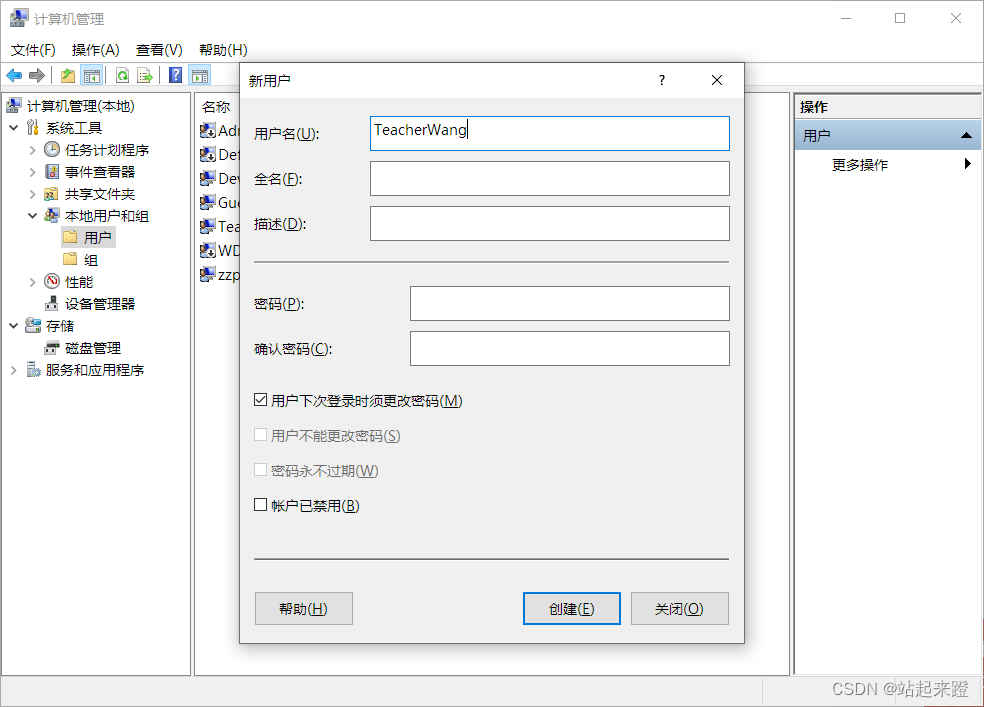
SQL Server添加用户登录
我们可以模拟一下让这个数据库可以给其它人使用 1、在计算机中添加一个新用户TeacherWang 2、在Sql Server中添加该计算机用户的登录权限 exec sp_grantlogin LAPTOP-61GDB2Q7\TeacherWang -- 之后这个计算机用户也可以登录数据库了 3、添加数据库的登录用户和密码࿰…...
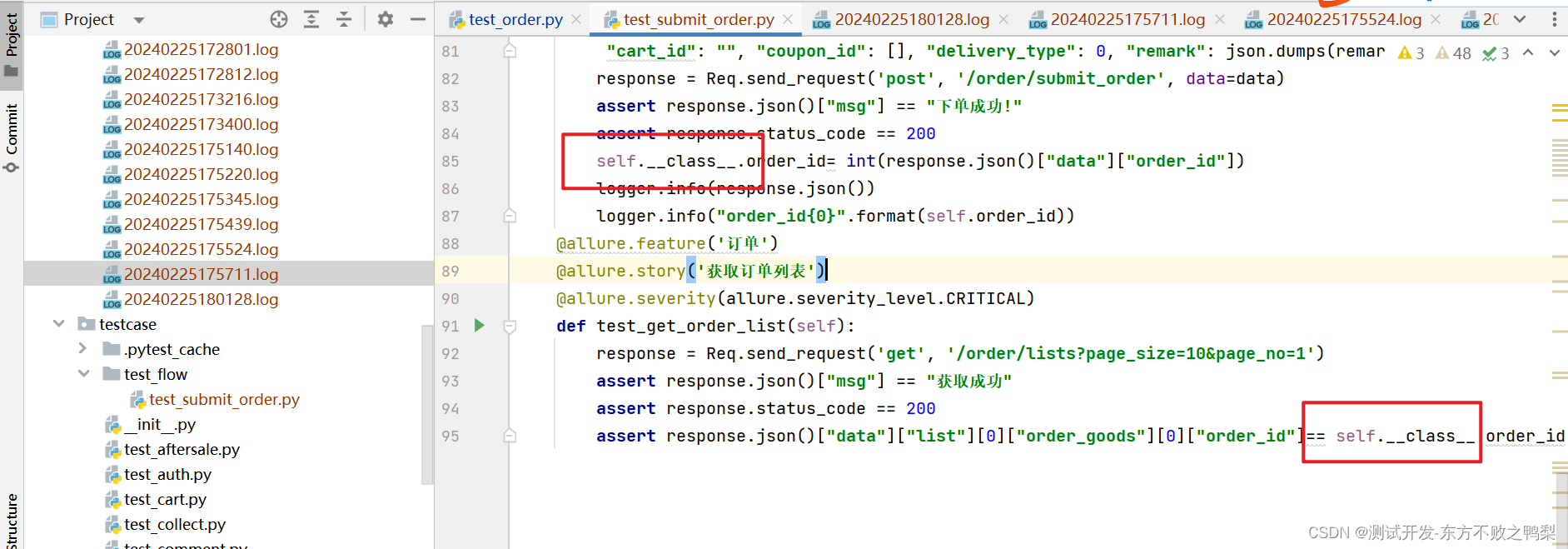
pytest如何在类的方法之间共享变量?
在pytest中,setup_class是一个特殊的方法,它用于在类级别的测试开始之前设置一些初始化的状态。这个方法会在类中的任何测试方法执行之前只运行一次。 当你在setup_class中使用self来修改类属性时,你实际上是在修改类的一个实例属性。在Pyth…...
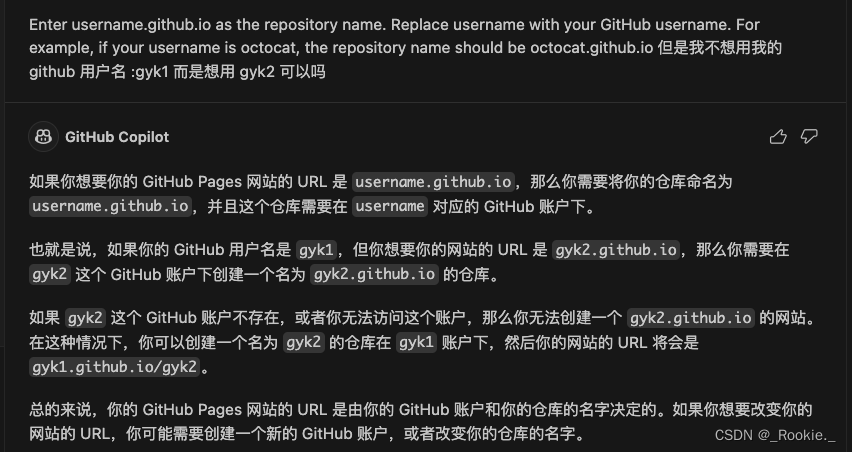
配置前端项目到 github-pages
Quickstart for GitHub Pages - GitHub Docs...

VSCode使用教程
文章目录 VSCode简介VSCode下载安装配置语言环境CJavaPython VSCode偏好配置中文配置界面颜色字体大小快捷键 个人常规喜好 VSCode简介 VSCode(全称:Visual Studio Code)是一款由微软开发且跨平台的免费源代码编辑器。该软件支持语法高亮、代…...

vscode——本地配置(C和C++环境配置)(2)
vscode——本地配置(2) 配置C语言编译看看.json文件编译多个C文件C/C调试 今天我们继续来看vscode的配置,如果没看过上一次的文章,大家可以点击: https://blog.csdn.net/qq_67693066/article/details/136315696 配置C语…...

【从零开始学习重要知识点 | 第一篇】快速了解什么是幂等性以及常见解决方案
前言: 当我们在设计和实现分布式系统时,幂等性是一个非常重要的概念。幂等性可以简单地理解为:对于同一操作,不论执行多少次,产生的影响都是相同的。这个概念在分布式系统中非常重要,因为在这种环境下&…...
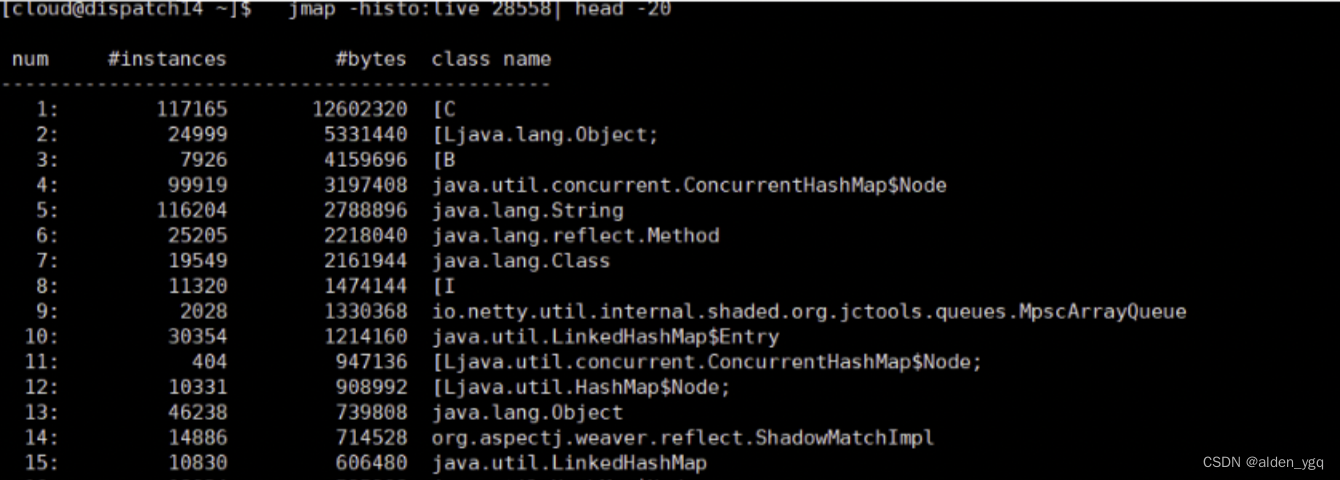
Jvm之内存泄漏
1 内存溢出 1.1 概念 java.lang.OutOfMemoryError,是指程序在申请内存时,没有足够的内存空间供其使用,出现OutOfMemoryError。产生该错误的原因主要包括:JVM内存过小。程序不严密,产生了过多的垃圾。 程序体现: 内…...

尚硅谷webpack5笔记2
Loader 原理 loader 概念 帮助 webpack 将不同类型的文件转换为 webpack 可识别的模块。 loader 执行顺序 分类pre: 前置 loadernormal: 普通 loaderinline: 内联 loaderpost: 后置 loader执行顺序4 类 loader 的执行优级为:pre > normal > inline > post 。相…...
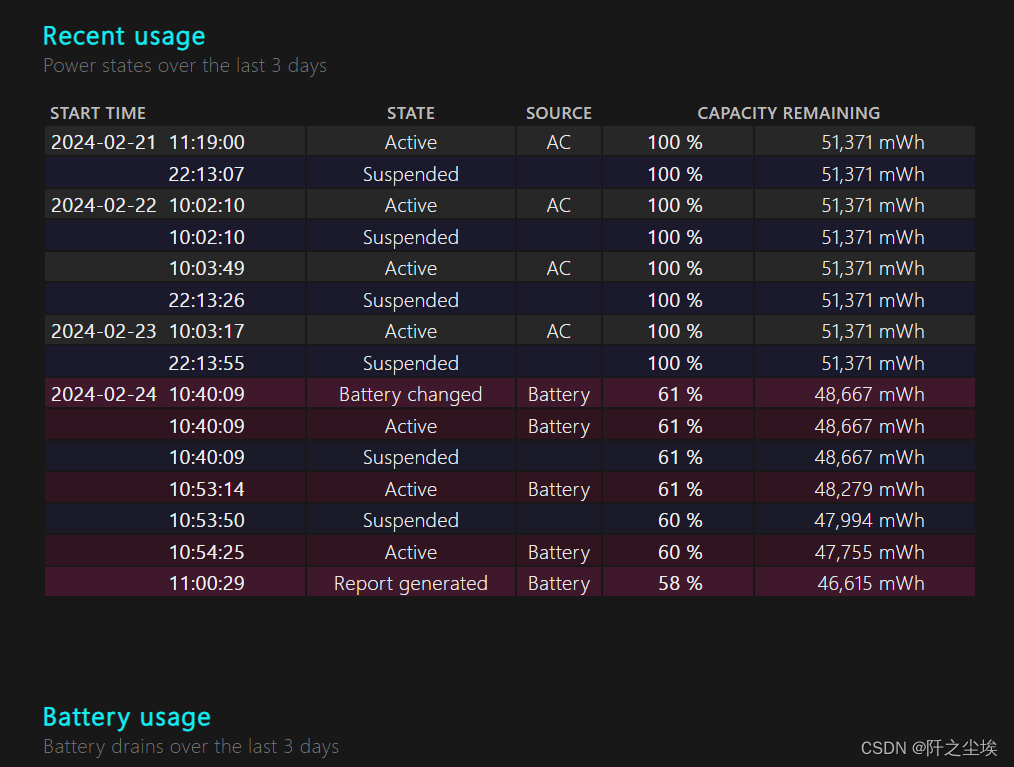
笔记本Win 10系统查看电池健康状况
博主最近换了个笔记本电池,之前的电池容量明显变小了很多,而且出现了轻微鼓包的情况。所以用gpt问了一下怎么用系统的方法查看电池情况。 在Windows 10系统中,您可以通过以下步骤来查看笔记本电脑电池的健康状况: 打开命令提示符&…...

算法--动态规划(线性DP、区间DP)
这里写目录标题 tip数组下标从0开始还是从1开始 数学三角形介绍算法思想例题代码 最长上升子序列介绍算法思想例题代码 最长公共子序列介绍算法思想例题代码 tip 数组下标从0开始还是从1开始 如果代码中涉及到数组下标为i-1(有时候哪怕不是同一个数组也符合情况&am…...

【ArcGIS】统计格网中不同土地利用类型占比
基于ArcGIS统计格网中不同土地利用类型占比 数据准备ArcGIS操作步骤1、创建渔网(Create Fishnet)2、建立唯一标识3、选择格网4、提取不同类别土地利用类型5、各类用地面积计算 参考另:可能出现的问题总结Q1:ArcGIS获取唯一值&…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
