LED电子显示屏连接方式解析
LED电子显示屏作为现代化数字展示设备的重要组成部分,其连接方式对于显示效果和稳定性至关重要。正确选择和实施连接方式不仅可以确保LED显示屏系统的正常运行,还可以提高其可靠性和持久性。本文将介绍LED电子显示屏常见的连接方式,以帮助读者更好地了解并选择适合自己需求的连接方式。

1. 并联连接方式:
在并联连接方式中,LED显示屏的各个模块或单元是平行连接的。每个模块都直接连接到电源,并且在显示数据方面是独立的。这种连接方式简单直观,易于维护和扩展。同时,如果一个模块出现故障,其余模块仍可正常工作,不会影响整个显示屏的运行。然而,由于每个模块都有自己的电源连接,这可能导致电源线过多,增加了布线的复杂性。你了解LED屏幕的前维护和后维护吗?

2. 串联连接方式:
在串联连接方式中,LED显示屏的各个模块或单元是依次连接的,就像串珠一样。数据和电源从一个模块传递到另一个模块,直到整个显示屏完成。串联连接方式减少了布线的数量和复杂性,使得整个系统更加简洁。但是,如果其中一个模块发生故障,可能会影响整个显示屏的工作,因此需要及时检修和更换故障模块。什么是LED显示模块?

3. 混合连接方式:
混合连接方式结合了并联和串联连接的优点。显示屏的某些部分可能是并联连接的,而其他部分则是串联连接的。这种方式可以在一定程度上平衡两种连接方式的优缺点,提高系统的稳定性和可靠性。

4. 交叉阵列连接方式:
交叉阵列连接方式旨在提高LED显示屏的可靠性和稳定性。LED模块以交叉的方式连接,以确保即使出现故障,也不会影响整个显示屏的工作。这种连接方式适用于对显示效果和可靠性要求较高的场合,如大型户外广告牌和舞台背景等。LED广告牌是如何工作的?
总结:
LED电子显示屏的连接方式多种多样,每种连接方式都有其独特的优劣势。在选择适合的连接方式时,需要考虑到显示屏的尺寸、应用场景、布线环境等因素。同时,在安装和维护过程中,确保连接方式的正确性和稳定性至关重要,这将直接影响到LED显示屏的性能和使用寿命。因此,深入了解并选择适合自己需求的连接方式,是确保LED显示屏系统正常运行的关键所在。
谢谢你的观看,希望可以解决你遇到的问题。如果你想了解:认识黑灯LED显示屏与白灯LED显示屏,请点击阅读。
关注我!带你了解更多的led显示屏知识。
相关文章:

LED电子显示屏连接方式解析
LED电子显示屏作为现代化数字展示设备的重要组成部分,其连接方式对于显示效果和稳定性至关重要。正确选择和实施连接方式不仅可以确保LED显示屏系统的正常运行,还可以提高其可靠性和持久性。本文将介绍LED电子显示屏常见的连接方式,以帮助读者…...
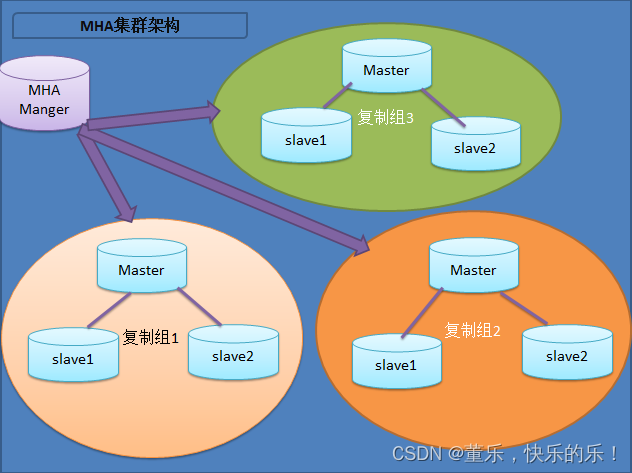
Mysql运维篇(五) 部署MHA--主机环境配置
一路走来,所有遇到的人,帮助过我的、伤害过我的都是朋友,没有一个是敌人。如有侵权,请留言,我及时删除! 大佬博文 https://www.cnblogs.com/gomysql/p/3675429.html MySQL 高可用(MHA&#x…...
)
Offer必备算法09_分治快排_四道力扣OJ(快排三路划分)
目录 分治快排算法原理 ①力扣75. 颜色分类 解析代码 ②力扣912. 排序数组 解析代码 ③力扣215. 数组中的第K个最大元素 解析代码 ④力扣LCR 159. 库存管理 III(剑指 Offer . 最小的k个数) 解析代码 本篇完。 分治快排算法原理 分治就是分而治…...
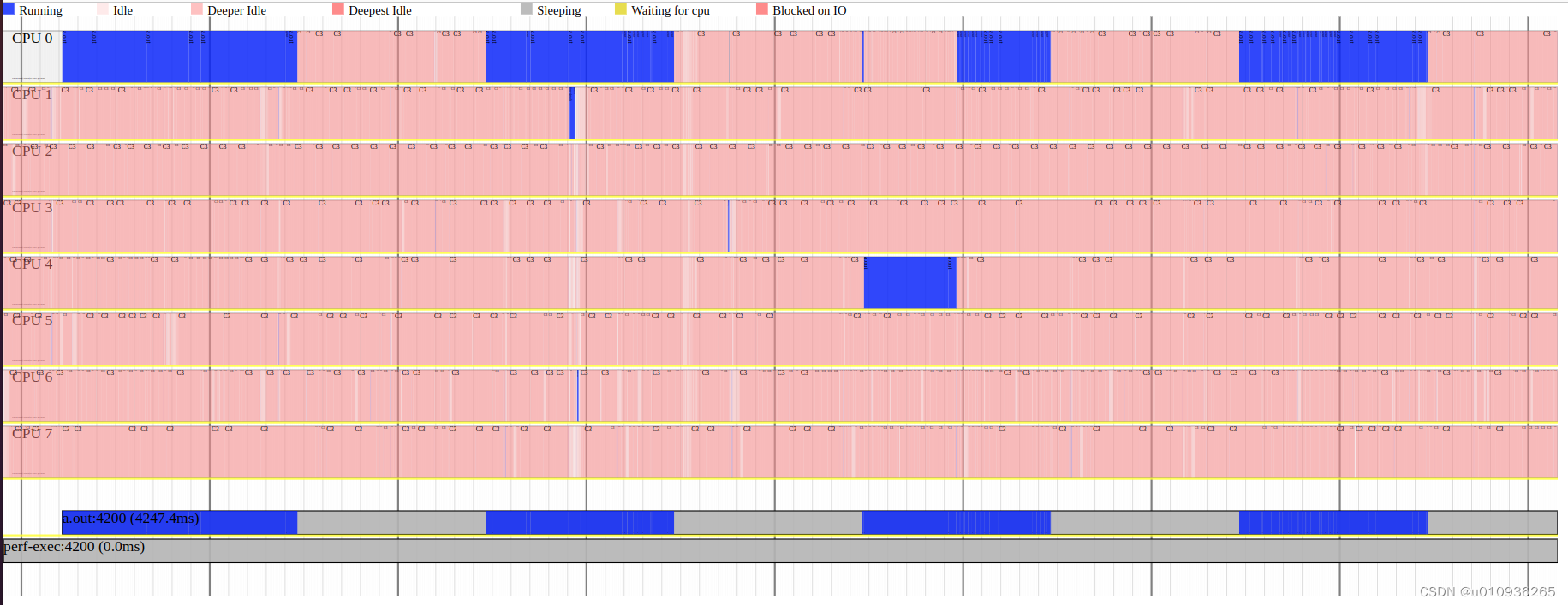
Linux下性能分析的可视化图表工具
1 sar 和sadf 1.1 简介 sar命令可以记录系统下的常见活动信息,例如CPU使用率、网络统计数据、Block I/O数据、内存使用情况 等。 sar命令的“-o [file_name]”参数可以将系统活动数据记录到file_name文件,然后通过sadf来解析,sadf命令的“-g…...

泽攸科技JS系列高精度台阶仪在半导体领域的应用
泽攸科技JS系列高精度台阶仪是一款先进的自主研发的国产台阶仪,采用了先进的扫描探针技术。通过扫描探针在样品表面上进行微观测量,台阶仪能够准确获取表面形貌信息。其工作原理基于探针与样品表面的相互作用力,通过测量探针的微小位移&#…...

c++实现栈和队列类
c实现栈和队列类 栈(Stack)Stack示意图Stack.cpp 队列(queue)queue 示意图queue.cpp 栈(Stack) Stack示意图 Stack.cpp #pragma once #include "ListStu.cpp"template<typename T> class Stack { public: /* * void push(T& tDate)* 参数一 :…...

MySQL优化之索引下推
(/≧▽≦)/~┴┴ 嗨~我叫小奥 ✨✨✨ 👀👀👀 个人博客:小奥的博客 👍👍👍:个人CSDN ⭐️⭐️⭐️:传送门 🍹 本人24应届生一枚,技术和水平有限&am…...

【Java程序设计】【C00338】基于Springboot的银行客户管理系统(有论文)
基于Springboot的银行客户管理系统(有论文) 项目简介项目获取开发环境项目技术运行截图 项目简介 这是一个基于Springboot的银行客户管理系统,本系统有管理员、员工以及用户二种角色; 管理员:个人中心、管理员管理、客…...

C语言中大小写字母的转化
目录 C语言中大小写字母的转化 一、引言 二、C语言中的大小写转换函数 toupper()函数 tolower()函数 三、注意事项 四、总结 C语言中大小写字母的转化 一、引言 在C语言编程中,字符的处理是一个重要的环节。字符包括字母、数字、标点符号等,其中…...

Camunda7.18流程引擎启动出现Table ‘camunda_platform_docker.ACT_GE_PROPERTY‘的解决方案
文章目录 1、问题描述2、原因分析3、解决方案3.1、方案一:降低mysql版本3.2、方案二:增加nullCatalogMeansCurrent参数(推荐) 4、总结 1、问题描述 需要在docker中,部署Camunda流程引擎。通过启动脚本camunda-platfor…...

红队打靶:DR4G0N B4LL打靶思路详解(vulnhub)
目录 写在开头 第一步:主机发现 第二步:Web渗透 第三步:curl批量访问(无果) 第四步:Vulnhub目录发现 第五步: 图片隐写破解 第六步:ssh私钥登录 第七步:变量劫持提…...
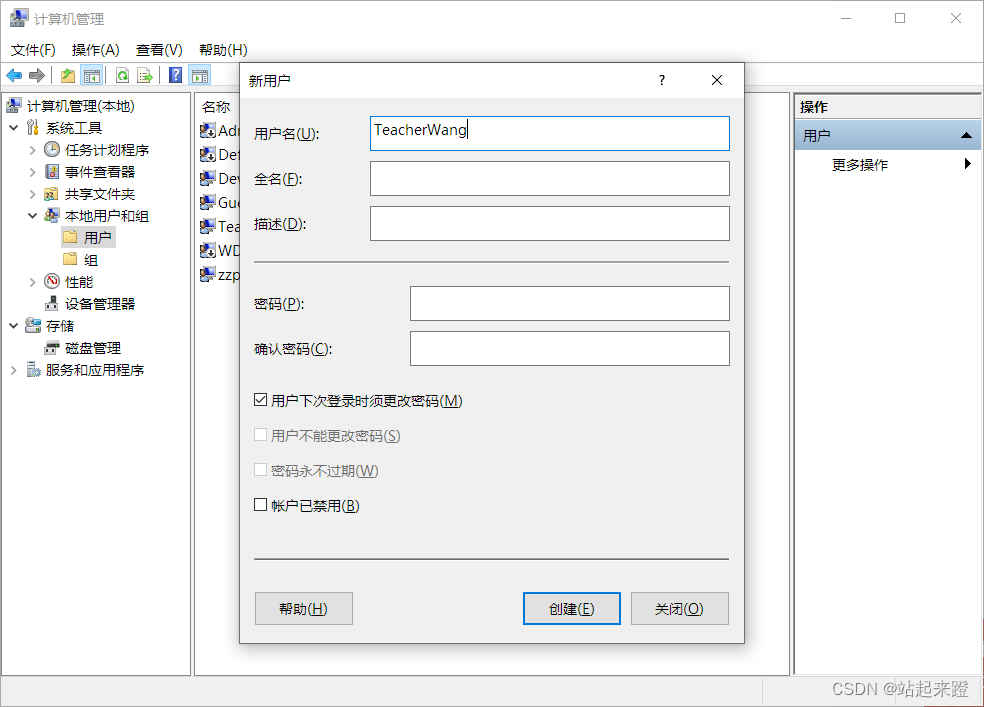
SQL Server添加用户登录
我们可以模拟一下让这个数据库可以给其它人使用 1、在计算机中添加一个新用户TeacherWang 2、在Sql Server中添加该计算机用户的登录权限 exec sp_grantlogin LAPTOP-61GDB2Q7\TeacherWang -- 之后这个计算机用户也可以登录数据库了 3、添加数据库的登录用户和密码࿰…...
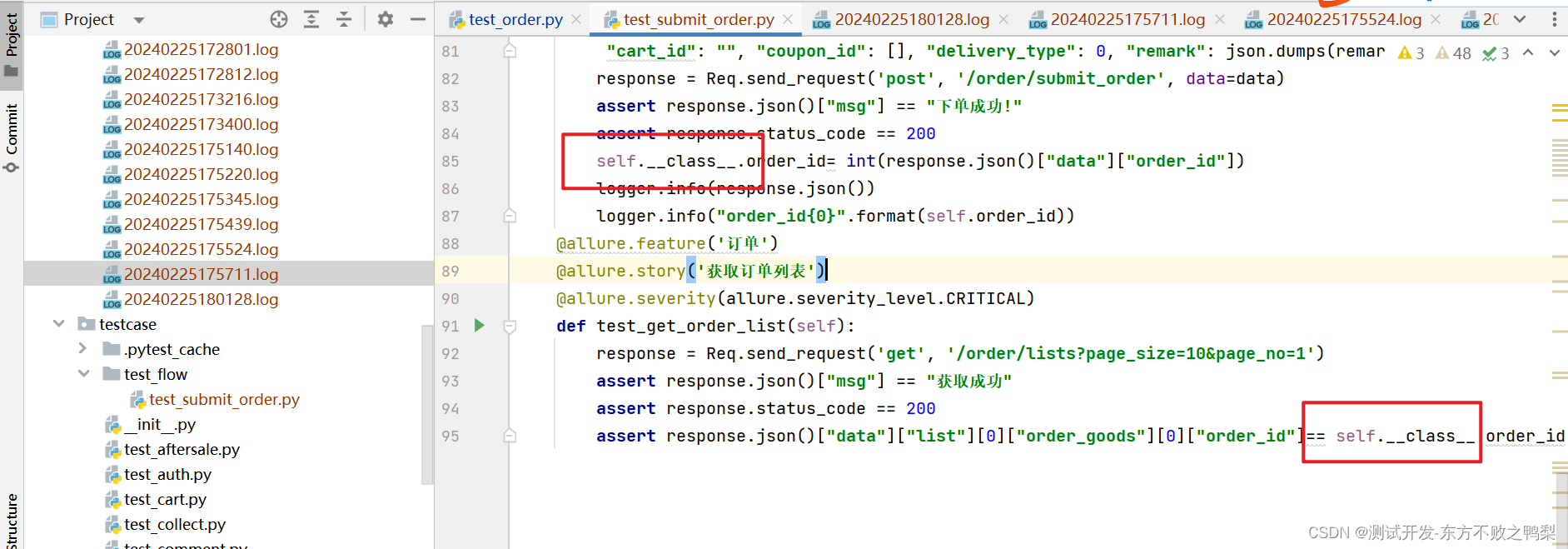
pytest如何在类的方法之间共享变量?
在pytest中,setup_class是一个特殊的方法,它用于在类级别的测试开始之前设置一些初始化的状态。这个方法会在类中的任何测试方法执行之前只运行一次。 当你在setup_class中使用self来修改类属性时,你实际上是在修改类的一个实例属性。在Pyth…...
配置前端项目到 github-pages
Quickstart for GitHub Pages - GitHub Docs...

VSCode使用教程
文章目录 VSCode简介VSCode下载安装配置语言环境CJavaPython VSCode偏好配置中文配置界面颜色字体大小快捷键 个人常规喜好 VSCode简介 VSCode(全称:Visual Studio Code)是一款由微软开发且跨平台的免费源代码编辑器。该软件支持语法高亮、代…...

vscode——本地配置(C和C++环境配置)(2)
vscode——本地配置(2) 配置C语言编译看看.json文件编译多个C文件C/C调试 今天我们继续来看vscode的配置,如果没看过上一次的文章,大家可以点击: https://blog.csdn.net/qq_67693066/article/details/136315696 配置C语…...

【从零开始学习重要知识点 | 第一篇】快速了解什么是幂等性以及常见解决方案
前言: 当我们在设计和实现分布式系统时,幂等性是一个非常重要的概念。幂等性可以简单地理解为:对于同一操作,不论执行多少次,产生的影响都是相同的。这个概念在分布式系统中非常重要,因为在这种环境下&…...
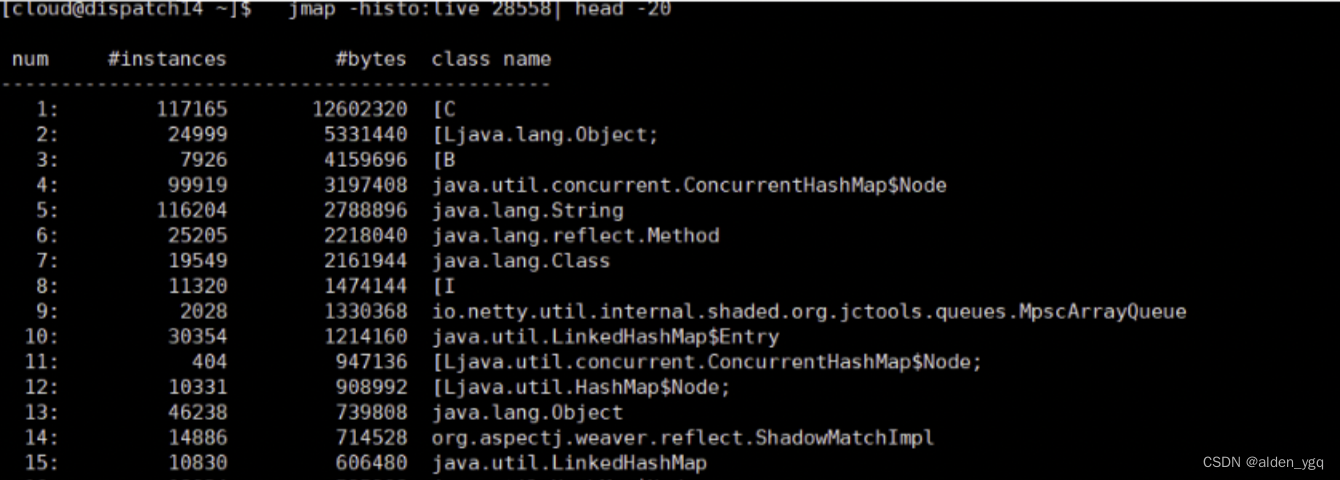
Jvm之内存泄漏
1 内存溢出 1.1 概念 java.lang.OutOfMemoryError,是指程序在申请内存时,没有足够的内存空间供其使用,出现OutOfMemoryError。产生该错误的原因主要包括:JVM内存过小。程序不严密,产生了过多的垃圾。 程序体现: 内…...

尚硅谷webpack5笔记2
Loader 原理 loader 概念 帮助 webpack 将不同类型的文件转换为 webpack 可识别的模块。 loader 执行顺序 分类pre: 前置 loadernormal: 普通 loaderinline: 内联 loaderpost: 后置 loader执行顺序4 类 loader 的执行优级为:pre > normal > inline > post 。相…...
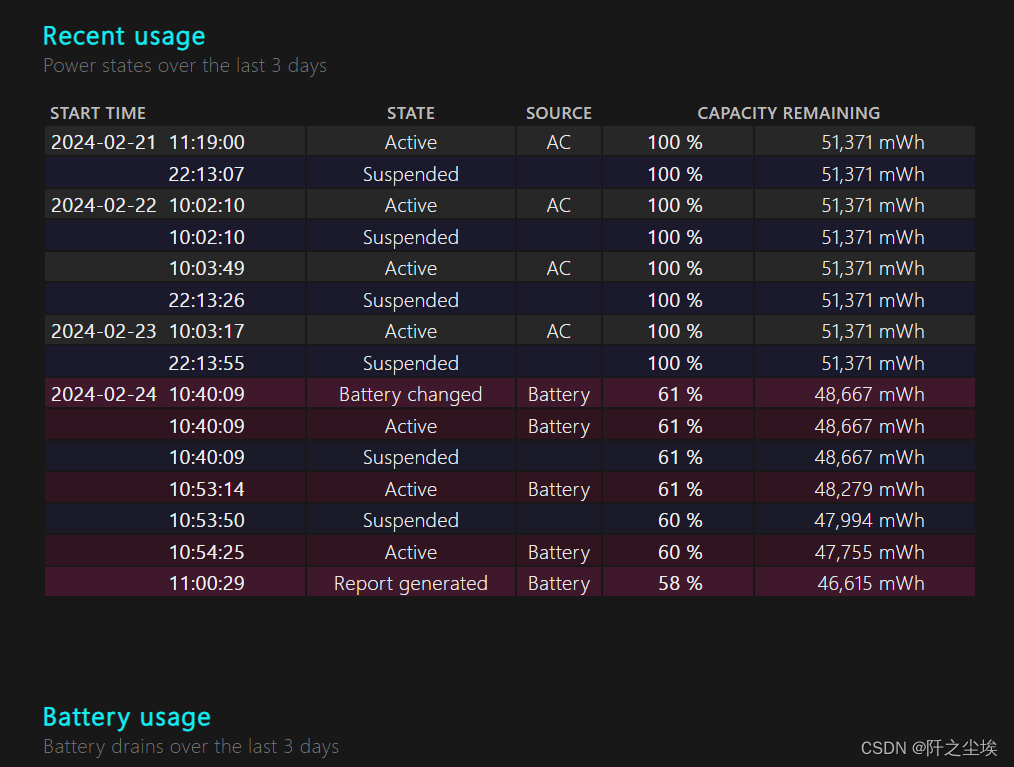
笔记本Win 10系统查看电池健康状况
博主最近换了个笔记本电池,之前的电池容量明显变小了很多,而且出现了轻微鼓包的情况。所以用gpt问了一下怎么用系统的方法查看电池情况。 在Windows 10系统中,您可以通过以下步骤来查看笔记本电脑电池的健康状况: 打开命令提示符&…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
