Eigen-Matrix矩阵
Eigen-Matrix矩阵
- 一、概述
- 二、矩阵的前三个模板参数
- 三、向量
- 四、动态维度参数
- 五、构造函数
- 六、索引访问器
- 七、逗号初始化
- 八、矩阵维度调整
- 九、赋值和调整大小
- 十、固定尺寸vs.动态尺寸
- 十一、可选模板参数
- 十二、方便预定义
一、概述
在Eigen中,所有矩阵和向量都是矩阵模板类的对象。向量只是矩阵的一种特殊情况,要么有一行,要么有一列。矩阵就是一个二维数表,可以有多行多列。
二、矩阵的前三个模板参数
Matrix类有六个模板参数,但现在只需要了解前三个参数就足够了。剩下的三个参数都有默认值,我们暂时不碰它们,我们将在下面讨论它们。
Matrix的三个必备模板参数为:
Matrix<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>
- 参数Scalar, 标量是标量类型,即系数的类型。也就是说,如果你想要一个浮点数的矩阵,在这里选择float。有关所有支持的标量类型的列表,以及如何扩展对新类型的支持,请参阅标量类型。
- RowsAtCompileTime和ColsAtCompileTime是在编译时已知的矩阵的行数和列数(如果在编译时不知道该数,请参见下文)。
Eigen提供了许多方便的类型来涵盖通常的情况。例如,Matrix4f是一个4x4的浮点数矩阵。Eigen是这样定义的:
typedef Matrix<float, 4, 4> Matrix4f;
三、向量
如上所述,在Eigen中,向量只是矩阵的一种特殊情况,要么有一行,要么有一列。它们只有一列的情况是最常见的;这样的向量称为列向量,通常简称为向量。在另一种情况下,它们只有一行,它们被称为行向量。
例如,方便的类型pedef Vector3f是一个3个浮点数的(列)向量。Eigen对其定义如下:
typedef Matrix<float, 3, 1> Vector3f;
我们还为行向量提供了方便的类型,例如:
typedef Matrix<int, 1, 2> RowVector2i;
四、动态维度参数
当然,Eigen并不局限于在编译时已知维数的矩阵。RowsAtCompileTime和ColsAtCompileTime模板参数可以采用特殊值Dynamic,这表示在编译时大小未知,因此必须作为运行时变量处理。
在Eigen学术语中,这样的尺寸被称为动态尺寸;而在编译时已知的大小称为固定大小。例如,方便类型pedef MatrixXd,表示具有动态大小的双精度矩阵,定义如下:
typedef Matrix<double, Dynamic, Dynamic> MatrixXd;
同样,我们定义了一个自解释的类型pedef VectorXi如下:
typedef Matrix<int, Dynamic, 1> VectorXi;
你可以完美地拥有固定数量的行和动态数量的列,如下所示:
Matrix<float, 3, Dynamic>
五、构造函数
默认构造函数始终可用,从不执行任何动态内存分配,也从不初始化矩阵系数。你可以这样做:
Matrix3f a;
MatrixXf b;
在这里,
- a 是一个3 × 3矩阵,其系数为未初始化的浮点[9]数组;
- b 是一个动态大小的矩阵,其大小目前为0 × 0,其系数数组还没有被分配。
构造函数也可以接受大小。对于矩阵,总是先传递行数。对于向量,只需传递向量的大小。它们用给定的大小分配系数数组,但不初始化系数本身:
MatrixXf a(10,15);
VectorXf b(30);
在这里,
- a 是一个10x15的动态大小矩阵,具有已分配但当前未初始化的系数。
- b 是一个大小为30的动态大小向量,具有已分配但当前未初始化的系数。
为了在固定大小和动态大小的矩阵之间提供统一的API,在固定大小的矩阵上使用这些构造函数是合法的,即使在这种情况下传递大小是无用的。所以这是合法的:
Matrix3f a(3,3);
这是一个无操作。
矩阵和向量也可以从系数列表初始化。在c++ 11之前,此功能仅限于固定大小的小列或大小不超过4的向量:
Vector2d a(5.0, 6.0);
Vector3d b(5.0, 6.0, 7.0);
Vector4d c(5.0, 6.0, 7.0, 8.0);
如果启用c++ 11,可以通过传递任意数量的系数来初始化任意大小的固定大小的列向量或行向量:
Vector2i a(1, 2); // A column vector containing the elements {1, 2}
Matrix<int, 5, 1> b {1, 2, 3, 4, 5}; // A row-vector containing the elements {1, 2, 3, 4, 5}
Matrix<int, 1, 5> c = {1, 2, 3, 4, 5}; // A column vector containing the elements {1, 2, 3, 4, 5}
在一般情况下,无论是固定大小还是运行时大小的矩阵和向量,系数必须按行分组,并作为初始化列表的初始化列表传递:
MatrixXi a { // construct a 2x2 matrix{1, 2}, // first row{3, 4} // second row
};
Matrix<double, 2, 3> b {{2, 3, 4},{5, 6, 7},
};
对于列向量或行向量,允许隐式转置。这意味着可以从单行初始化列向量:
VectorXd a {{1.5, 2.5, 3.5}}; // A column-vector with 3 coefficients
RowVectorXd b {{1.0, 2.0, 3.0, 4.0}}; // A row-vector with 4 coefficients
六、索引访问器
在eigen中,主要的系数访问器和变量是重载括号操作符。对于矩阵,总是先传递行索引。对于向量,只传递一个下标。编号从0开始。这个例子不言自明:
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::MatrixXd m(2,2);m(0,0) = 3;m(1,0) = 2.5;m(0,1) = -1;m(1,1) = m(1,0) + m(0,1);std::cout << "Here is the matrix m:\n" << m << std::endl;Eigen::VectorXd v(2);v(0) = 4;v(1) = v(0) - 1;std::cout << "Here is the vector v:\n" << v << std::endl;
}
输出:
Here is the matrix m:3 -1
2.5 1.5
Here is the vector v:
4
3
请注意,语法m(index)并不局限于向量,它也可用于一般矩阵,这意味着在系数数组中基于索引的访问。然而,这取决于矩阵的存储顺序。所有特征矩阵默认为列为主的存储顺序,但可以将其更改为行为主,请参阅存储顺序。
对于vector中的基于索引的访问,操作符 [ ] 也被重载,但请记住,c++不允许操作符 [ ] 接受多个参数。我们将运算符 [ ] 限制为向量,只有向量支持使用 [ ] 符号索引,因为c++语言中的一个笨拙会使 matrix[i,j] 编译成与 matrix[j] 相同的东西!
七、逗号初始化
可以使用所谓的逗号初始化语法方便地设置矩阵和向量系数。现在,知道这个例子就足够了:
Matrix3f m;
m << 1, 2, 3,4, 5, 6,7, 8, 9;
std::cout << m;
输出
1 2 3
4 5 6
7 8 9
八、矩阵维度调整
矩阵的当前大小可以通过rows()、cols()和size()来获取。这些方法分别返回行数、列数和系数数。通过resize()方法调整动态大小矩阵的大小。
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::MatrixXd m(2,5);m.resize(4,3);std::cout << "The matrix m is of size "<< m.rows() << "x" << m.cols() << std::endl;std::cout << "It has " << m.size() << " coefficients" << std::endl;Eigen::VectorXd v(2);v.resize(5);std::cout << "The vector v is of size " << v.size() << std::endl;std::cout << "As a matrix, v is of size "<< v.rows() << "x" << v.cols() << std::endl;
输出
The matrix m is of size 4x3
It has 12 coefficients
The vector v is of size 5
As a matrix, v is of size 5x1
如果实际矩阵大小没有改变,resize()方法是不操作的;否则它是破坏性的:系数的值可能会改变。如果你想要一个不改变系数的 resize()的 保守变体,使用conservativeResize(),更多细节请参阅本页。
为了API的一致性,所有这些方法在固定大小的矩阵上仍然可用。当然,您实际上无法调整固定大小的矩阵的大小。尝试将固定大小更改为实际不同的值将触发断言失败;但是下面的代码是合法的:
例如:输出:
#include <iostream>
#include <Eigen/Dense>int main()
{Eigen::Matrix4d m;m.resize(4,4); // no operationstd::cout << "The matrix m is of size "<< m.rows() << "x" << m.cols() << std::endl;
输出
The matrix m is of size 4x4
九、赋值和调整大小
赋值是使用操作符=将一个矩阵复制到另一个矩阵的操作。Eigen自动调整左手边矩阵的大小,使其与右手边矩阵的大小相匹配。例如:
MatrixXf a(2,2);
std::cout << "a is of size " << a.rows() << "x" << a.cols() << std::endl;
MatrixXf b(3,3);
a = b;
std::cout << "a is now of size " << a.rows() << "x" << a.cols() << std::endl
输出
a is of size 2x2
a is now of size 3x3
当然,如果左侧是固定大小,则不允许调整其大小。
如果您不希望发生这种自动调整大小(例如为了调试目的),您可以禁用它,请参阅此页。
十、固定尺寸vs.动态尺寸
什么时候应该使用固定大小(例如Matrix4f),什么时候应该使用动态大小(例如MatrixXf)?简单的答案是:对于非常小的尺寸尽可能使用固定大小,对于较大的尺寸或必须使用动态大小。对于较小的大小,特别是小于(大约)16的大小,使用固定大小对性能非常有益,因为它允许Eigen避免动态内存分配并展开循环。在内部,固定大小的特征矩阵只是一个普通数组,即做
Matrix4f mymatrix;
其实就是去做
float mymatrix[16];
这真的是零运行费用。相比之下,动态大小矩阵的数组总是在堆上分配,所以这样做
MatrixXf mymatrix(rows,columns);
等于做某事
float *mymatrix = new float[rows*columns];
除此之外,MatrixXf对象将其行数和列数存储为成员变量。
当然,使用固定大小的限制是,只有在编译时知道大小时才有可能。此外,对于足够大的大小,例如大于(大约)32的大小,使用固定大小的性能优势变得可以忽略不计。更糟糕的是,尝试在函数内部使用固定大小创建一个非常大的矩阵可能会导致堆栈溢出,因为Eigen会尝试将数组自动分配为局部变量,而这通常是在堆栈上完成的。最后,根据具体情况,当使用动态大小时,Eigen也可以更积极地尝试向量化(使用SIMD指令),请参阅向量化。
十一、可选模板参数
我们在本页开头提到,Matrix类接受六个模板参数,但到目前为止我们只讨论了前三个。其余三个参数为可选参数。下面是模板参数的完整列表:
Matrix<typename Scalar,int RowsAtCompileTime,int ColsAtCompileTime,int Options = 0,int MaxRowsAtCompileTime = RowsAtCompileTime,int MaxColsAtCompileTime = ColsAtCompileTime>
- Options是位字段。在这里,我们只讨论一个比特:RowMajor。它指定这种类型的矩阵使用行为主存储顺序;默认情况下,存储顺序是以列为主的。请参阅存储订单页面。例如,此类型表示行为主的3x3矩阵:
Matrix<float, 3, 3, RowMajor>
- MaxRowsAtCompileTime和MaxColsAtCompileTime在需要指定时非常有用,即使在编译时不知道矩阵的确切大小,但在编译时知道一个固定的上限。这样做的最大原因可能是为了避免动态内存分配。例如,下面的矩阵类型使用12个浮点数的普通数组,没有动态内存分配:
Matrix<float, Dynamic, Dynamic, 0, 3, 4>
十二、方便预定义
Eigen定义了以下矩阵类型:
都是用的 Matrix 不同模板参数,预定义为不同类型。
- MatrixNt :Matrix<type, N, N>.
例如, MatrixXi 实际上是 :Matrix<int, Dynamic, Dynamic>. - MatrixXNt :Matrix<type, Dynamic, N>.
例如, MatrixX3i 实际上是 :Matrix<int, Dynamic, 3>. - MatrixNXt :Matrix<type, N, Dynamic>.
例如, Matrix4Xd 实际上是 :Matrix<d, 4, Dynamic>. - VectorNt :Matrix<type, N, 1>.
例如, Vector2f 实际上是 :Matrix<float, 2, 1>. - RowVectorNt :Matrix<type, 1, N>.
例如, RowVector3d 实际上是 :Matrix<double, 1, 3>.
注意:
- N 可以是2、3、4或者X(表示动态 Dynamic ) 中的任意一个。
- t 可以是I (int)、f (float)、d (double)、cf (complex)或CD (complex)中的任意一个。虽然只为这五种类型定义了类型定义,但这并不意味着它们是唯一受支持的标量类型。例如,支持所有标准整数类型,请参阅标量类型。
相关文章:

Eigen-Matrix矩阵
Eigen-Matrix矩阵 一、概述二、矩阵的前三个模板参数三、向量四、动态维度参数五、构造函数六、索引访问器七、逗号初始化八、矩阵维度调整九、赋值和调整大小十、固定尺寸vs.动态尺寸十一、可选模板参数十二、方便预定义 一、概述 在Eigen中,所有矩阵和向量都是矩…...

蓝桥杯14届计算思维国赛U8组包含真题和答案
十四届蓝桥杯国赛考试计算思维 U8 组 答案在底部 第一题 以下选项中,( )是由美国计算机协会设立,对在计算机领域内作出重要贡献的个人授予的奖项 。A.图灵奖 C.菲尔兹奖 B.诺贝尔奖 D.普利策奖 第二题 希希去吃寿司。餐台上摆出了许多食物,可供大家自选。如下图所示。 …...
)
opencv内存溢出del释放变量 (python)
报错: cv2.error: OpenCV(3.4.17) D:\a\opencv-python\opencv-python\opencv\modules\core\src\alloc.cpp:73: error: (-4:Insufficient memory) Failed to allocate 12211548 bytes in function ‘cv::OutOfMemoryError’ 检查内存代码 import psutil# 获取当前进…...

【算法与数据结构】复杂度深度解析(超详解)
文章目录 📝算法效率🌠 算法的复杂度🌠 时间复杂度的概念🌉大O的渐进表示法。 🌠常见复杂度🌠常见时间复杂度计算举例🌉常数阶O(1)🌉对数阶 O(logN)🌉线性阶 O(N)&#x…...
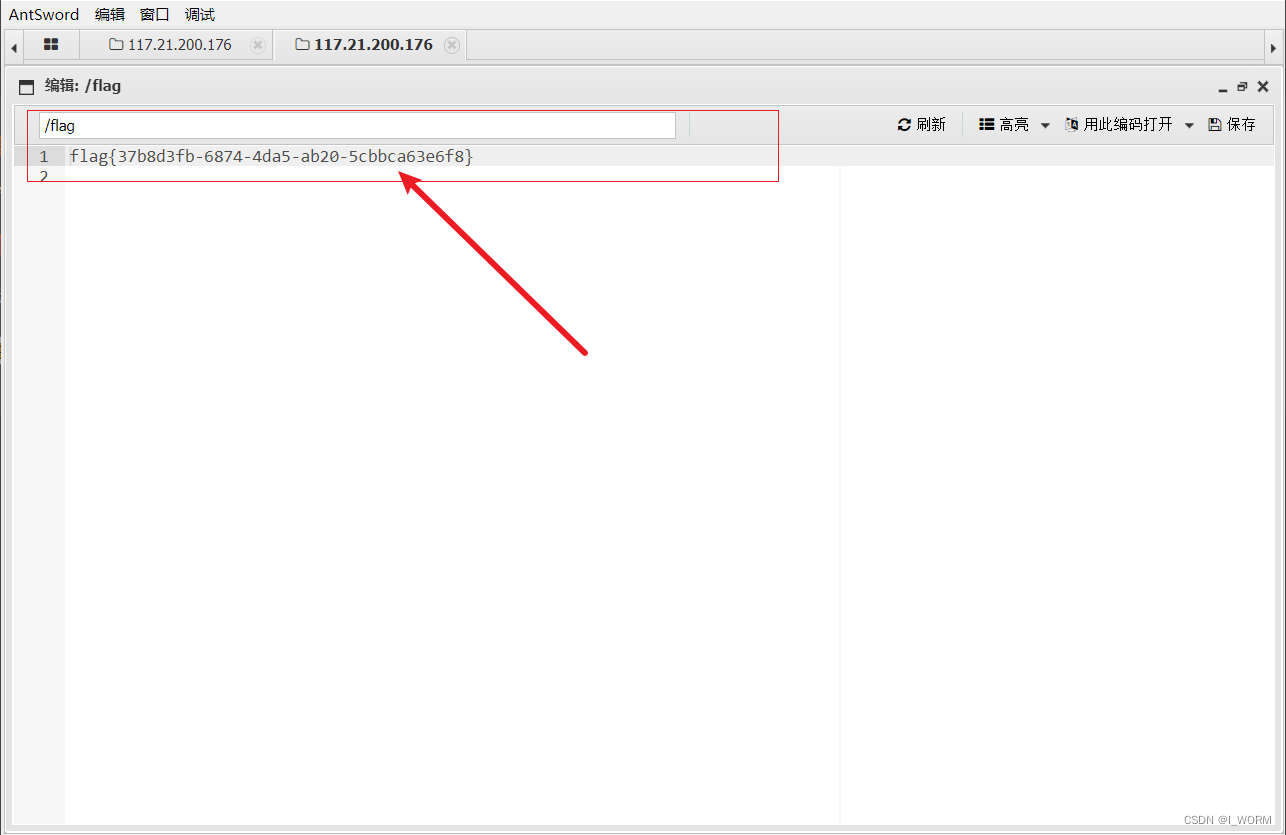
Upload-Labs-Linux1【CTF】
拿到这道题目一看,发现是upload靶场;这不简简单单吗;结果中间还是遇到了一些小问题 小坑总结:该关只识别标准php语法:<?php phpinfo()?>格式;即<?php ?> 不识别<? phpinfo()?> &…...

搜维尔科技:OptiTrack 提供了性能最佳的动作捕捉平台
OptiTrack 动画 我们的 Prime 系列相机和 Motive 软件相结合,产生了世界上最大的捕获量、最精确的 3D 数据和有史以来最高的相机数量。OptiTrack 提供了性能最佳的动作捕捉平台,具有易于使用的制作工作流程以及运行世界上最大舞台所需的深度。 无与伦比…...
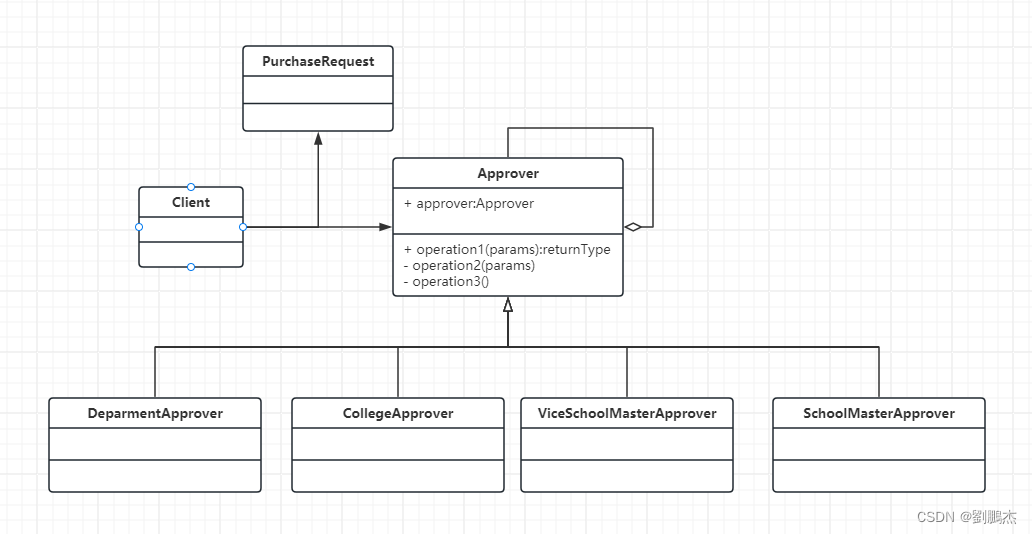
java设计模式之职责链模式
基本介绍 职责链模式(Chain of Responsibility Pattern)为请求创建了一个接收者对象的链。这种模式对请求的发送者和接收者进行解耦。职责链模式 又叫责任链模式,通常每个接收者都包含对另一个接收者的引用。如果一个对象不能处理该请求。那…...

连不上网的解决办法集--持续更新
连不上网的解决办法集–持续更新 1、有网卡,但网卡驱动失效 背景:有网络驱动但是依旧连不上网,只有inteV6有值,inte 没有值(正常应该有个ipv4的信息) 判断原因:可能是之前格式化磁盘驱动的时…...

Unity之PUN2插件实现多人联机射击游戏
目录 📖一、准备工作 📺二、UI界面处理 📱2.1 登录UI并连接PUN2服务器 📱2.2 游戏大厅界面UI 📱2.3 创建房间UI 📱2.4 进入房间UI 📱2.5 玩家准备状态 📱2.6 加载战斗场景…...
)
72_Pandas.DataFrame保存并读取带pickle的系列(to_pickle、read_pickle)
72_Pandas.DataFrame保存并读取带pickle的系列(to_pickle、read_pickle) 要将 pandas.DataFrame、pandas.Series 对象保存为 pickle 文件,请使用 to_pickle() 方法,并使用 pd.read_pickle() 函数读取保存的 pickle 文件。 在此对…...

Redis哨兵模式和Redis Cluster模式
文章目录 🔊博主介绍🥤本文内容Redis Cluster 模式支持自动故障转移功能吗?Redis Cluster 模式支持自动故障转移功能和哨兵有什么区别?Redis Cluster 模式和哨兵模式(Sentinel)在自动故障转移方面有一些关键…...
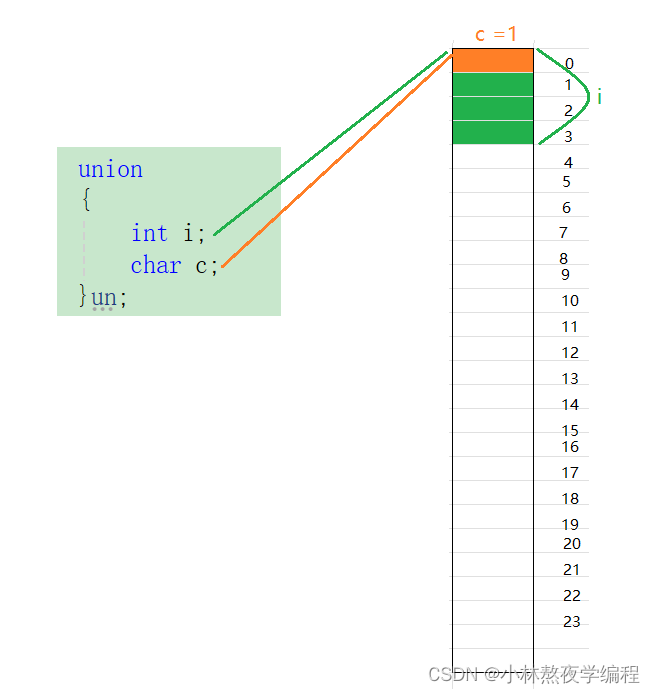
C语言第三十二弹---自定义类型:联合和枚举
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】 目录 1、联合体 1.1、联合体类型的声明 1.2、联合体的特点 1.3、相同成员的结构体和联合体对比 1.4、联合体大小的计算 1.5、联合的⼀个练习 2、枚举类型 …...

milvus upsert流程源码分析
milvus版本:v2.3.2 整体架构: Upsert 的数据流向: 1.客户端sdk发出Upsert API请求。 import numpy as np from pymilvus import (connections,Collection, )num_entities, dim 4, 3print("start connecting to Milvus") connections.connect("default",…...
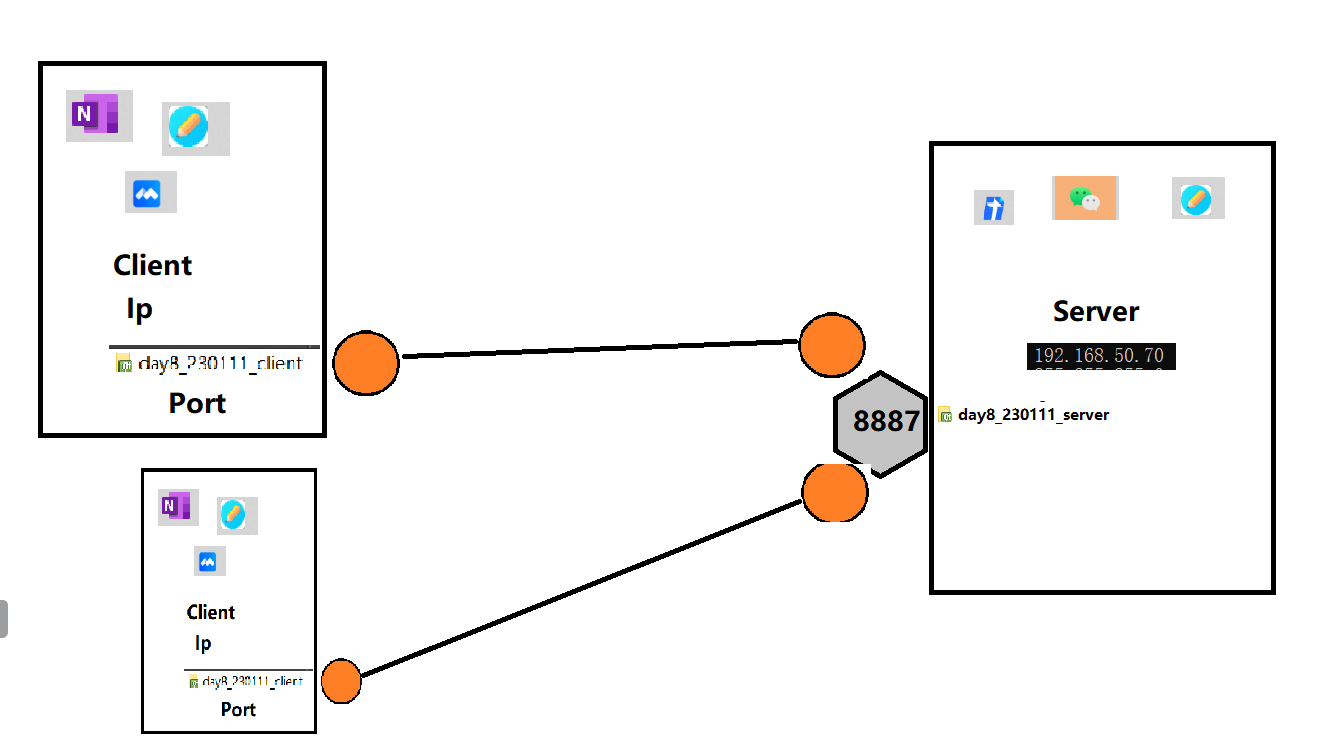
QT网络通信
九、网络 基础概念 1.1 TCP/UDP TCP/UDP UDP TCP 协议相同点:都存在于传输层,全双工通信 TCP:全双工通信、面向连接、可靠 TCP(即传输控制协议):是一种面向连接的传输层协议,它能提供高可靠性通…...
案例分析|山西某光伏发电站轨道巡检机器人解决方案
随着光伏发电技术的不断发展,光伏变电站配电室作为能量转换和输送的关键节点,承担着重要的电力分配和保护功能。然而,传统的人工巡检方式存在诸多问题,如巡检周期长、效率低、安全风险高等,已经无法满足光伏变电站配电…...
Apache POl
介绍 Apache POl是一个处理Miscrosoft Ofice各种文件格式的开源项目。简单来说就是,我们可以使用 POI 在 Java 程序中对Miscrosoft Office各种文件进行读写操作,一般情况下,POI都是用于操作 Excel 文件。 Apache POl 的应用场景 1.银行网银系统导出交易…...

高防服务器托管应注意什么
选择高防服务器托管主要考虑的因素:1.服务商的服务器大小。2.服务器的防御值大小。3.服务器机房的位置以及机房的资质。 具体内容如下: 1.服务器大小是按照U来定的,U是一种表示服务器外部尺寸的单位(计量单位:高度或厚…...
swagger-ui.html报错404,解决办法
swagger-ui.html报错404,解决办法!现在后端开发项目中,为了节省时间,使用swagger插件,可以方便的快捷生成接口文档。但是如果你在请求前端页面路径比如:http://127.0.0.1:7777/swagger-ui.html。找不到。那是因为你的配…...

golang 函数式编程库samber/mo使用: Future
golang 函数式编程库samber/mo使用: Future 如果您对samber/mo库不了解, 请先阅读第一篇 Option 本节讲述Future的使用,它可以帮助我们处理异步编程问题。 示例 我们先来看看下面代码的示例, 注释解释了每一步的操作。 packa…...
----Mongodb特有的查询方法)
【Spring连载】使用Spring Data访问 MongoDB(十四)----Mongodb特有的查询方法
【Spring连载】使用Spring Data访问 MongoDB(十四)----Mongodb特有的查询方法 一、定义通用查询方法二、MongoDB特有的查询方法2.1 地理空间查询Geo-spatial Queries2.2 基于JSON的查询方法和字段限制2.3 使用SpEL表达式的基于JSON的查询2.4 全文检索查询…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
