[数据结构 C++] AVL树的模拟实现

文章目录
- 1、AVL树
- 1.1 AVL树的概念
- 2、AVL树节点的定义
- 3、AVL树的插入和旋转
- 3.1 左单旋
- 左旋代码实现
- 3.2 右单旋
- 右旋代码实现
- 3.3 右左双旋
- 右左双旋的代码实现
- 3.4 左右双旋
- 左右双旋的代码实现
- 3.5 insert接口实现
- 4、判断是否为AVL树
- 判断AVL树的代码实现
- 5、AVL树的性能
问题引入:
在上一篇文章中,我们提到了二叉搜索树在插入时,可能会形成单边树,会降低二叉搜索的性能。因此我们需要平衡二叉搜索树,降低二叉搜索树的高度,使得二叉搜索树趋于一颗完全二叉树的样子,这样就可以提高二叉搜索树的性能。本篇文章就来介绍一种平衡二叉树,AVL树。
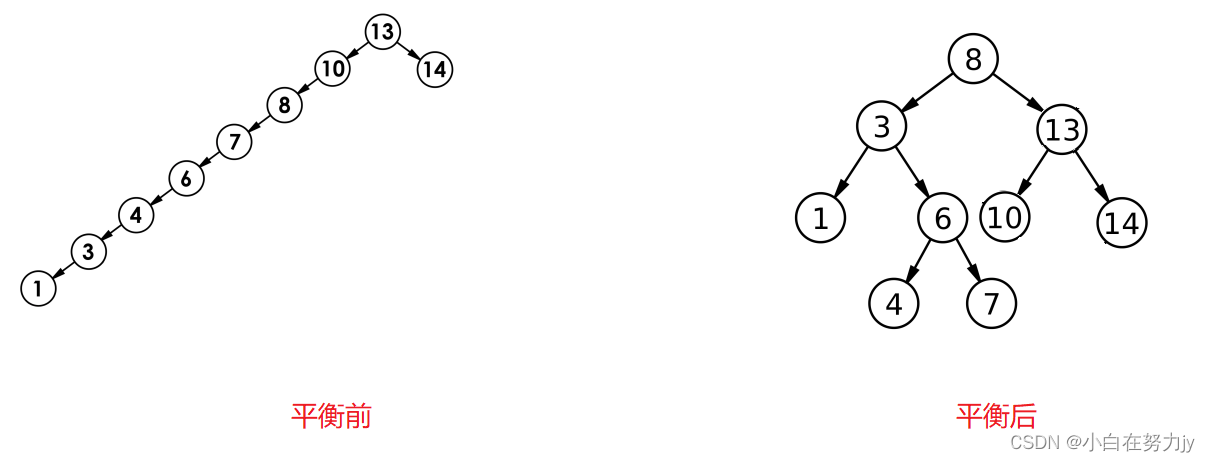
1、AVL树
1.1 AVL树的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
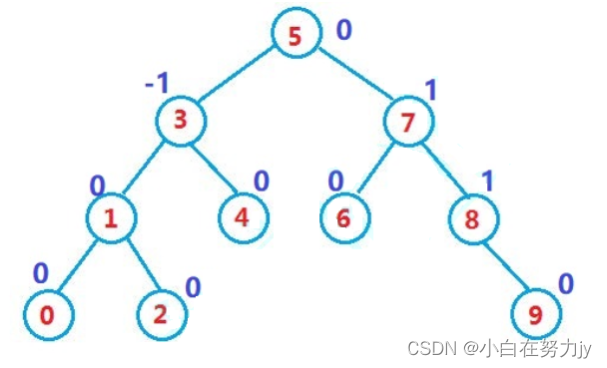
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在O(log N),搜索时间复杂度O(log N)。
我们了解了AVL树的基本规则后,下面我们来实现一下AVL树。
2、AVL树节点的定义
template <class K, class V>
struct AVLTreeNode
{AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;pair<K, V> _kv;// 右子树 - 左子树 的高度差int _bf; // 平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}
};
3、AVL树的插入和旋转
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么
AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
当某个节点的平衡因子被修改为2的时候,就需要旋转来调节,因此就存在一下四种旋转方式:
3.1 左单旋
我们将 左单旋的情况抽象出来,如下图所示:

当 h >= 0,且parent->_bf == 2 && subR->_bf == 1时,触发左旋。
在这个图中,只能是在 c 子树新增,才能触发左旋的条件parent->_bf == 2 && subR->_bf == 1。此时进行左旋。
如果是在 b 子树新增,那么仅仅左旋是不够的,
旋转步骤:将60的左树变为30的右树,将60的左树变为30,最后将parent和subR的平衡因子变为0就完成了左旋。
左旋代码实现
// 左单旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;if (_root == parent) // 父节点就是根节点{_root = subR;subR->_parent = nullptr;}else // 子树情况{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}// 修改平衡因子parent->_bf = subR->_bf = 0;
}
3.2 右单旋
我们将 右单旋的情况抽象出来,如下图所示:
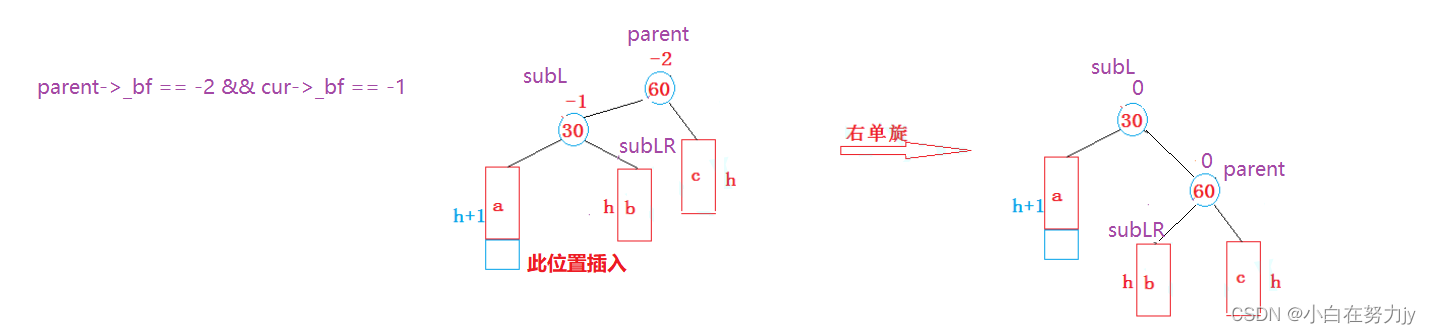
当 h >= 0,且 parent->_bf == 2 && subL->_bf == -1时,触发右旋。
在这个图中,只能是在 a子树新增,才能触发右旋的条件parent->_bf == -2 && subL->_bf == -1。此时进行右旋。
如果是在 b 子树新增,那么仅仅右旋是不够的。
旋转步骤:将30的右树接到60的左树并断开与30的链接,再将60接到30的右树,并将60的父节点改为3,最后再调整parent与SubL的平衡因子为0,就完成整个右旋。
右旋代码实现
// 右单旋
void RotateR(Node* parent)
{Node* parentParent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (_root == parent) // 父节点是根节点{_root = subL;subL->_parent = nullptr;}else // 子树情况{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}// 修改平衡因子parent->_bf = subL->_bf = 0;
}
3.3 右左双旋
我们将 右左双旋的所有情况抽象出来,如下图所示:
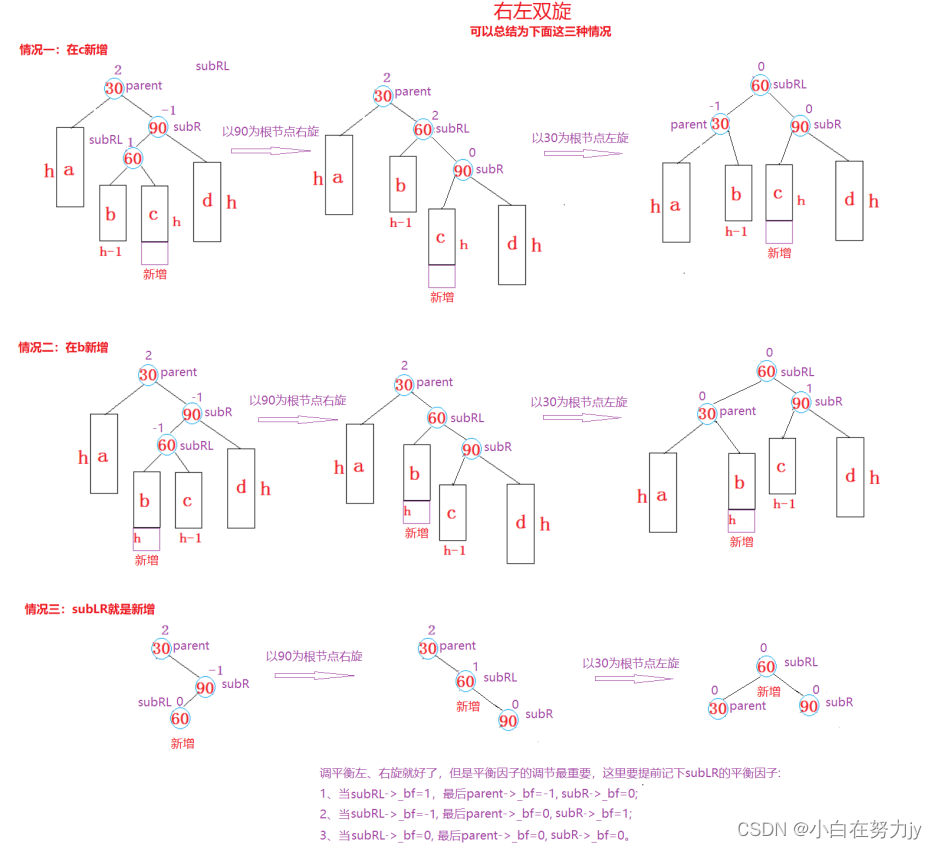
右左双旋的本质是先将子树右旋,让右侧一侧高,再进行整体的左旋,这样就完成了高度的调整。
双旋的插入位置可以是 b/c 子树,此类型插入之后就会触发右左双旋。
旋转步骤:直接复用右旋,再复用左旋即可。不过旋转的基点不同,右旋是以subR为基点,左旋是以parent为基点旋转的。旋转就完成了,难点在于平衡因子的调节。
平衡因子的调节:
这里主要是 记下subRL最初的平衡因子,它的平衡因子就代表了插入节点是在subRL的左边还是右边插入的,由此可以推出最终的parent与subR的平衡因子。
- 当subRL->_bf = 1时,最后parent->_bf = -1,subR->_bf = 0,subRL->_bf = 0;
- 当subRL->_bf = -1时,最后parent->_bf = 0,subR->_bf = 1,subRL->_bf = 0;
- 当subRL->_bf = 0时,最后parent->_bf = 0,subR->_bf = 0,subRL->_bf = 0;
右左双旋的代码实现
// 右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0) // subRL 就是插入的{parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == 1) // subRL 右边边插入{parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1) // subRL 左边插入{parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else{assert(false);}
}
3.4 左右双旋
我们将 右左双旋的所有情况抽象出来,如下图所示:
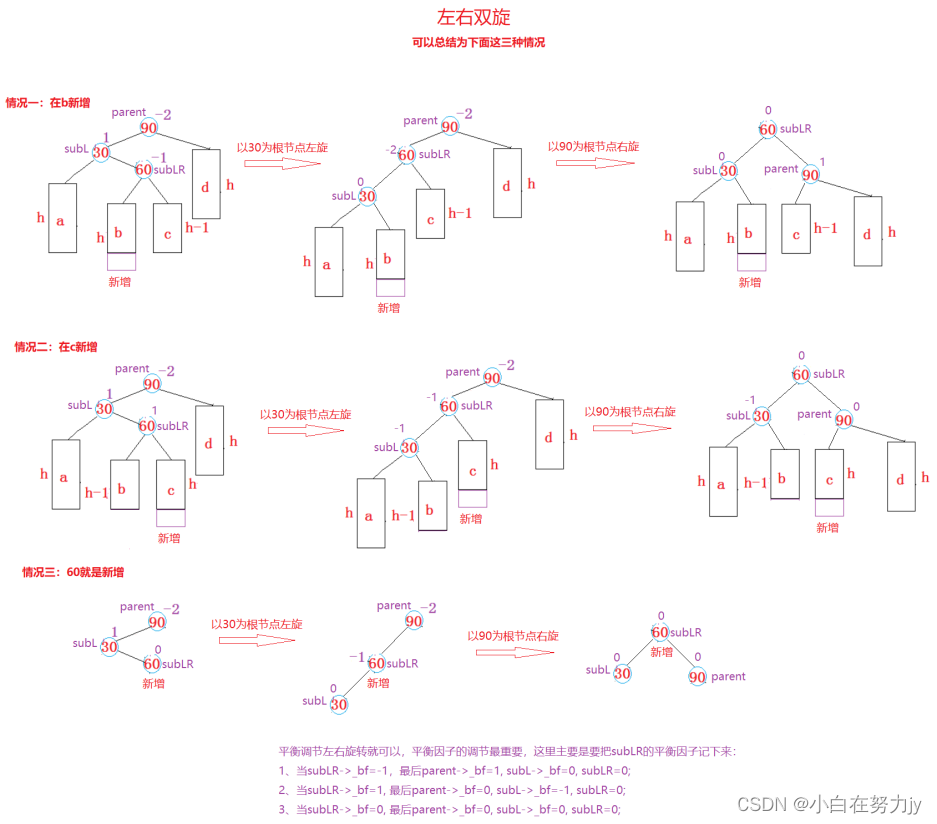
左右双旋与右左双旋的思路是差不多的,我们来看看。
左右双旋的本质是先将子树左旋,让左侧一侧高,在进行整体的右旋,这样就完成了高度的调整。
双旋的插入位置可以是 b/c 子树,此类型插入之后就会触发左右双旋。
旋转步骤:直接复用左旋,再复用右旋即可。不过旋转的基点不同,右旋是以subR为基点,左旋是以parent为基点旋转的。旋转就完成了,难点也是在于平衡因子的调节。
平衡因子的调节:
这里主要是 记下subLR最初的平衡因子,它的平衡因子就代表了插入节点是在subLR的左边还是右边插入的,由此可以推出最终的parent与subL的平衡因子。
- 当subLR->_bf = 1时,最后parent->_bf = 1,subL->_bf = 0,subLR->_bf = 0;
- 当subLR->_bf = 1时,最后parent->_bf = 0,subL->_bf = -1,subLR->_bf = 0;
- 当subLR->_bf = 0时,最后parent->_bf = 0,subL->_bf = 0,subLR->_bf = 0;
左右双旋的代码实现
// 左右双旋
void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (0 == bf){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (1 == bf){parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if (-1 == bf){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}
}
3.5 insert接口实现
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;// 1、先找到插入的位置while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}// 2、new一个节点,并与parent链接起来cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}// 3、调平横 —— 旋转 + 平衡因子的调节while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (0 == parent->_bf){break;}else if (parent->_bf == -1 || parent->_bf == 1){cur = parent;parent = parent->_parent;}else if (parent->_bf == -2 || parent->_bf == 2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}// 1、旋转让这颗子树平衡了// 2、旋转降低了这颗子树的高度,恢复到跟插入前一样的高度,所以对上一层没有影响,不用继续更新break;}else{assert(false);}}return true;
}
4、判断是否为AVL树
AVL树的本质是搜索二叉树 + 平衡机制,所以验证步骤:
1、首先判断是否为搜索树,写一个中序遍历,看看是不是升序即可;
2、按照AVL树的性质来判断:
- 每个节点的左右子树高度差绝对值小于等于1;
- 节点的平衡因子是否正确;
判断AVL树的代码实现
bool _IsBalance(Node* pRoot)
{if (pRoot == nullptr)return true;int leftHeight = _Height(pRoot->_left);int rightHeight = _Height(pRoot->_right);if (rightHeight - leftHeight != pRoot->_bf){cout << pRoot->_kv.first << "平衡因子异常" << endl;return false;}return rightHeight - leftHeight < 2&& _IsAVLTree(pRoot->_left)&& _IsAVLTree(pRoot->_right);
}size_t _Height(Node* pRoot)
{if (pRoot == nullptr)return 0;int leftHeight = _Height(pRoot->_left);int rightHeight = _Height(pRoot->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}void _InOrder(Node* pRoot)
{if (pRoot == nullptr)return;_InOrder(pRoot->_left);cout << pRoot->_kv.first << " ";_InOrder(pRoot->_right);
}
5、AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这样可以保证查询时高效的时间复杂度,即O(log N)。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
AVL树的实现代码放在代码仓库:https://gitee.com/xiaobai-is-working-hard-jy/data-structure/tree/master/AVLTree
相关文章:

[数据结构 C++] AVL树的模拟实现
文章目录 1、AVL树1.1 AVL树的概念 2、AVL树节点的定义3、AVL树的插入和旋转3.1 左单旋左旋代码实现 3.2 右单旋右旋代码实现 3.3 右左双旋右左双旋的代码实现 3.4 左右双旋左右双旋的代码实现 3.5 insert接口实现 4、判断是否为AVL树判断AVL树的代码实现 5、AVL树的性能 问题引…...
)
深入理解ngx_http_proxy_connect_module模块(下)
目录 5. 源码分析5.1 模块的初始化代码5.2 请求入口点函数分析5.2.1 ngx_http_proxy_connect_post_read_handler5.2.2 ngx_http_proxy_connect_handler5.3 域名解析回调5.4 向上游服务器发起连接5.4.1 ngx_http_proxy_connect_process_connect5.4.2 ngx_http_proxy_connect_wri…...

HTTP详解(HTTP的特点,状态码,工作原理,GET和POST的区别,如何解决无状态通信)!!!
文章目录 一、HTTP协议简介二、HTTP的主要特点三、HTTP之URL四、Request和Respons五、HTTP的状态码六、HTTP工作原理七、GET和POST请求的区别八、解决HTTP无状态通信——Cookie和Session 一、HTTP协议简介 HTTP协议是Hyper Text Transfer Protocol(超文本传输协议&…...

【QT+QGIS跨平台编译】之五十七:【QGIS_CORE跨平台编译】—【VECTOR_TILE生成】
文章目录 一、protoc二、生成来源三、构建过程一、protoc Protocol Buffers(简称 protobuf)是一种轻量级、高效的数据序列化框架,它可以将结构化数据序列化为二进制格式,同时还可以进行反序列化和数据压缩。相比于 XML 和 JSON 等传统的文本序列化格式,protobuf 采用二进制…...
2024年腾讯云优惠政策_腾讯云TOP10优惠活动
腾讯云服务器多少钱一年?62元一年起,2核2G3M配置,腾讯云2核4G5M轻量应用服务器218元一年、756元3年,4核16G12M服务器32元1个月、312元一年,8核32G22M服务器115元1个月、345元3个月,腾讯云服务器网txyfwq.co…...
SpringMVC 学习(二)之第一个 SpringMVC 案例
目录 1 通过 Maven 创建一个 JavaWeb 工程 2 配置 web.xml 文件 3 创建 SpringMVC 配置文件 spring-mvc.xml 4 创建控制器 HelloController 5 创建视图 index.jsp 和 success.jsp 6 运行过程 7 参考文档 1 通过 Maven 创建一个 JavaWeb 工程 可以参考以下博文&#x…...
qt5与qt6的cmake区别
文章目录 使用cmake构建qt项目,坑很多。一是本身就麻烦,二是,确实坑,因为不同的qtcreator版本,选了不同的kits(套件) 生成的CMakeList.txt文件也不一样。 如果可以的话都选择Qt6的相关选项&…...

【计算机网络】一些乱七八糟内容
MAC Media Access Control 用于在局域网(LAN)或广域网(WAN)中实现设备自动接入网络 "载波侦听多路访问"(Carrier Sense Multiple Access) CSMA/CD 是CSMA的升级版本,加入了序列号检测机制。 CSMA/CA 是CSM…...
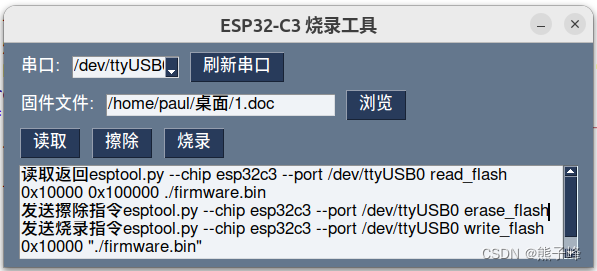
基于ESP32的MicroPython项目量产烧写指南
背景 前段时间用MicroPython开发了一个项目,硬件是ESP32-C3,目前准备量产,我需要提供固件以供加工厂批量烧录,需要把我有程序的板子里的程序读出来,然后下到别的板子上,以下做这件事情的过程记录。 1.固件…...
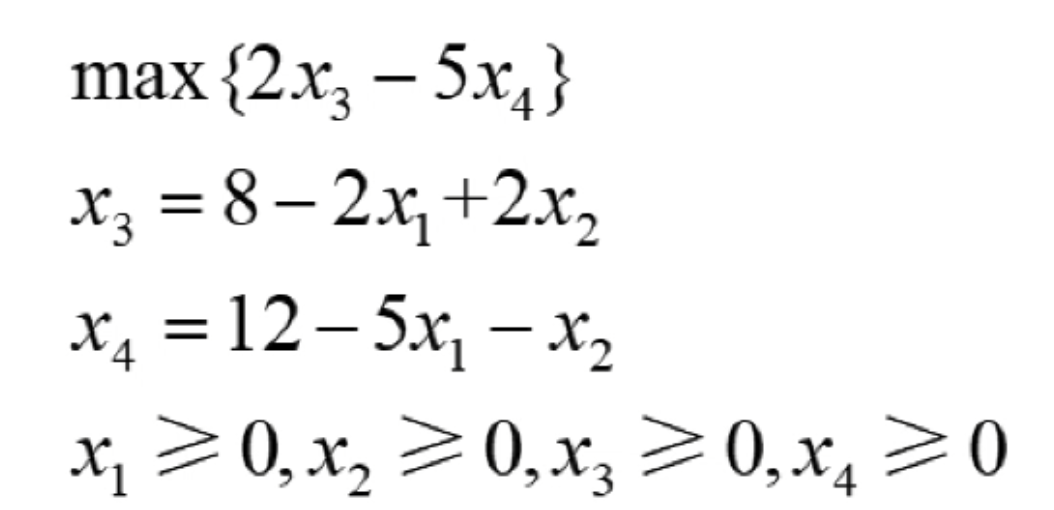
线性规划的标准型转换
对于任意给定的线性规划的问题,其实其本身可能是不符合线性规划标准型的需求的,但是如果通过一系列的等价变化的话,是可以将该问题转换为标准型的线性规划问题,例如如下的线性规划问题: 添加图片注释,不超过 140 字&am…...

机器学习:探寻智能化时代的科技奇迹
在数字化浪潮席卷全球的今天,机器学习已然成为科技领域的一颗璀璨明星,引领着人工智能不断向前发展。那么,机器学习究竟是什么?它为何能在众多科技中脱颖而出,成为改变世界的力量?本文将带您一探究竟&#…...

《Flask入门教程》学习笔记
《Flask入门教程》官网:https://tutorial.helloflask.com/ 目录 第一章:准备工作第二章:Hello, Flask!第三章:模板第四章:静态文件第五章:数据库第六章:模板优化第七章:表单第八章&a…...

go语言基础 -- map的定义与使用
map的定义与使用 map声明基础语法map的基本使用map的遍历map切片map排序 map声明基础语法 // map的声明 var xxx_map map[key_type]value_typemap的key可以是基本数据类型,channel,接口,结构体,数组,但不能是slice&am…...

讯方·智汇云校第五期名师班火热报名中!
第三期名师班回顾 授课情况 课堂上,同学们热情高涨,积极参与互动。他们紧跟名师的步伐,深入探索云服务的奥秘。张梁老师在为同学们讲述完知识点后,会根据所讲知识给同学们布置对应的实验,由同学们分组讨论练习。 每…...

为什么企业需要使用云电子邮箱?
作为一家机构的负责人,您比大多数人都清楚,您的工作日不会在下午5点就结束。很可能,当您的员工已经打卡下班回家很久之后,您还在以这样或那样的方式继续工作。作为一名企业主,埋头苦干对您来说并不是什么新鲜事&#x…...
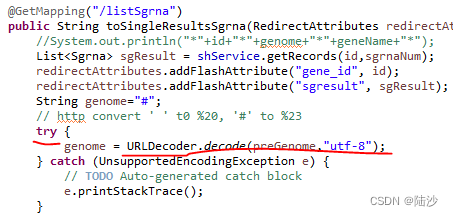
[DEBUG] spring boot-如何处理链接中的空格等特殊字符
问题: get或者post中提交的内容可能有空格、#等特殊字符,不做处理的话可能解析错误。 解决: html中: <a th:href"{/listSgrna(id${item.getGeneId()},geneName${item.getGeneName()},genome${genome},sgrnaNum${sgrnaN…...
来实现定时导出 MySQL 数据库)
通过配置数据库事件(Event)来实现定时导出 MySQL 数据库
首先,确保 MySQL 服务器已启用事件调度器功能。你可以通过以下 SQL 语句查询: SHOW VARIABLES LIKE event_scheduler; 如果 event_scheduler 的值为 ON,则表示事件调度器已启用;如果为 OFF,则可以使用以下语句启用&…...

基于x86架构的OpenHarmony应用生态挑战赛等你来战!
为了更快速推进OpenHarmony在PC领域的进一步落地,加快x86架构下基于OpenHarmony的应用生态的繁荣,为北向应用开发者提供一个更加便捷的开发环境,推动OpenHarmony北向应用开发者的增加,助力OpenHarmony在PC领域实现新的突破&#x…...

LeetCode每日一题2673. Make Costs of Paths Equal in a Binary Tree
文章目录 一、题目二、题解 一、题目 You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left ch…...

贝叶斯分类器
贝叶斯分类器 1. 引言 贝叶斯分类器是一种基于贝叶斯定理的分类算法,它利用特征之间的关系和类别的先验概率来进行分类。贝叶斯分类器在文本分类、垃圾邮件过滤、医学诊断等领域有着广泛的应用。 贝叶斯分类算法是统计学的一种分类方法,是一类利用概率…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
