13 Codeforces Round 886 (Div. 4)G. The Morning Star(简单容斥)
G. The Morning Star
- 思路:用map记录x,y,以及y-x、y+x
- 从前往后统计一遍答案即可
- 公式 a n s + = c n t [ x ] + c n t [ y ] − 2 ∗ c n t [ x , y ] + c n t [ y + x ] + c n t [ y − x ] ans+=cnt[x]+cnt[y]-2 * cnt[x,y]+cnt[y+x]+cnt[y-x] ans+=cnt[x]+cnt[y]−2∗cnt[x,y]+cnt[y+x]+cnt[y−x]
- c n t [ x ] + c n y [ y ] − 2 ∗ c n t [ x , y ] cnt[x]+cny[y]-2 * cnt[x,y] cnt[x]+cny[y]−2∗cnt[x,y]是统计坐标轴方向的,-2倍是需要把本身这个点给减去容斥是减一倍,这里还需要把自己给挖掉
- c n t [ y + x ] + c n t [ y − x ] cnt[y+x]+cnt[y-x] cnt[y+x]+cnt[y−x]是统计对角线方向的。这也是一种常用的表示对角线的技巧
#include <bits/stdc++.h>#define int long long
#define rep(i, a, b) for(int i = (a); i <= (b); ++i)
#define fep(i, a, b) for(int i = (a); i >= (b); --i)
#define _for(i, a, b) for(int i=(a); i<(b); ++i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>/** 思路:用map记录x,y,以及y-x、y+x* 从前往后统计一遍答案即可*/
using namespace std;
const int maxn = 2e5 + 10;
pii a[maxn];void solve() {int n;cin>>n;map<int,int>cntx,cnty,cntd,cnts;map<pii,int>cnt;int ans=0;rep(i,1,n){cin>>a[i].x>>a[i].y;}sort(a+1,a+1+n);rep(i,1,n){int x=a[i].x,y=a[i].y;ans+=cntx[x];ans+=cnty[y];//容斥ans-=2*cnt[{x,y}];ans+=cntd[y-x];ans+=cnts[y+x];cntx[x]+=1;cnty[y]+=1;cntd[y-x]+=1;cnts[y+x]+=1;cnt[{x,y}]+=1;}cout<<ans*2<<endl;
}signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
// freopen("C:\\Users\\24283\\CLionProjects\\untitled2\\1.in", "r", stdin);int _;cin >> _;while (_--)solve();return 0;
}
相关文章:
G. The Morning Star(简单容斥))
13 Codeforces Round 886 (Div. 4)G. The Morning Star(简单容斥)
G. The Morning Star 思路:用map记录x,y,以及y-x、yx从前往后统计一遍答案即可公式 a n s c n t [ x ] c n t [ y ] − 2 ∗ c n t [ x , y ] c n t [ y x ] c n t [ y − x ] anscnt[x]cnt[y]-2 * cnt[x,y]cnt[yx]cnt[y-x] anscnt[x]…...

CLion 2023:专注于C和C++编程的智能IDE mac/win版
JetBrains CLion 2023是一款专为C和C开发者设计的集成开发环境(IDE),它集成了许多先进的功能,旨在提高开发效率和生产力。 CLion 2023软件获取 CLion 2023的智能代码编辑器提供了丰富的代码补全和提示功能,使您能够更…...
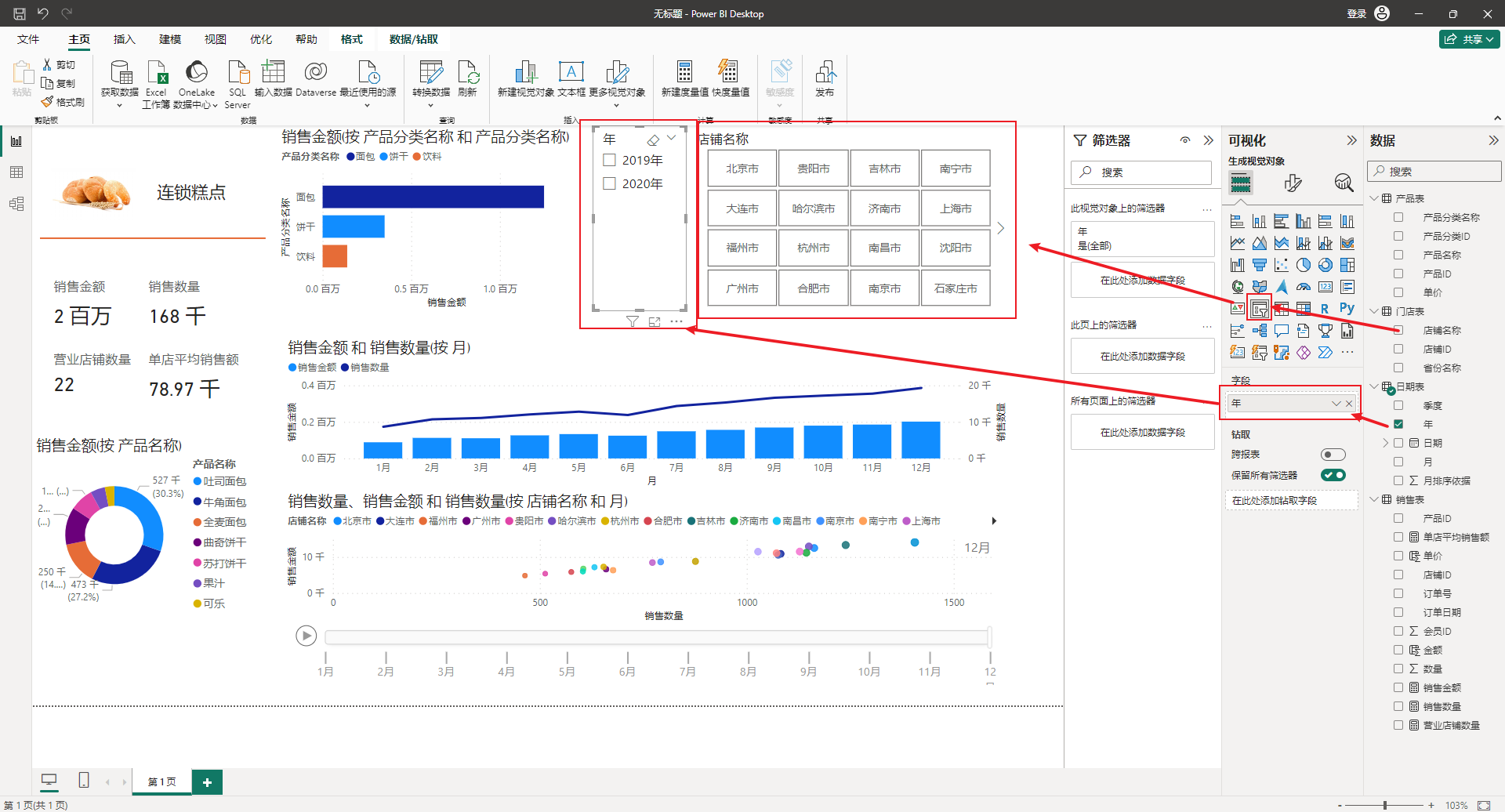
数据可视化基础与应用-02-基于powerbi实现连锁糕点店数据集的仪表盘制作
总结 本系列是数据可视化基础与应用的第02篇,主要介绍基于powerbi实现一个连锁糕点店数据集的仪表盘制作。 数据集描述 有一个数据集,包含四张工作簿,每个工作簿是一张表,其中可以销售表可以划分为事实表,产品表&am…...
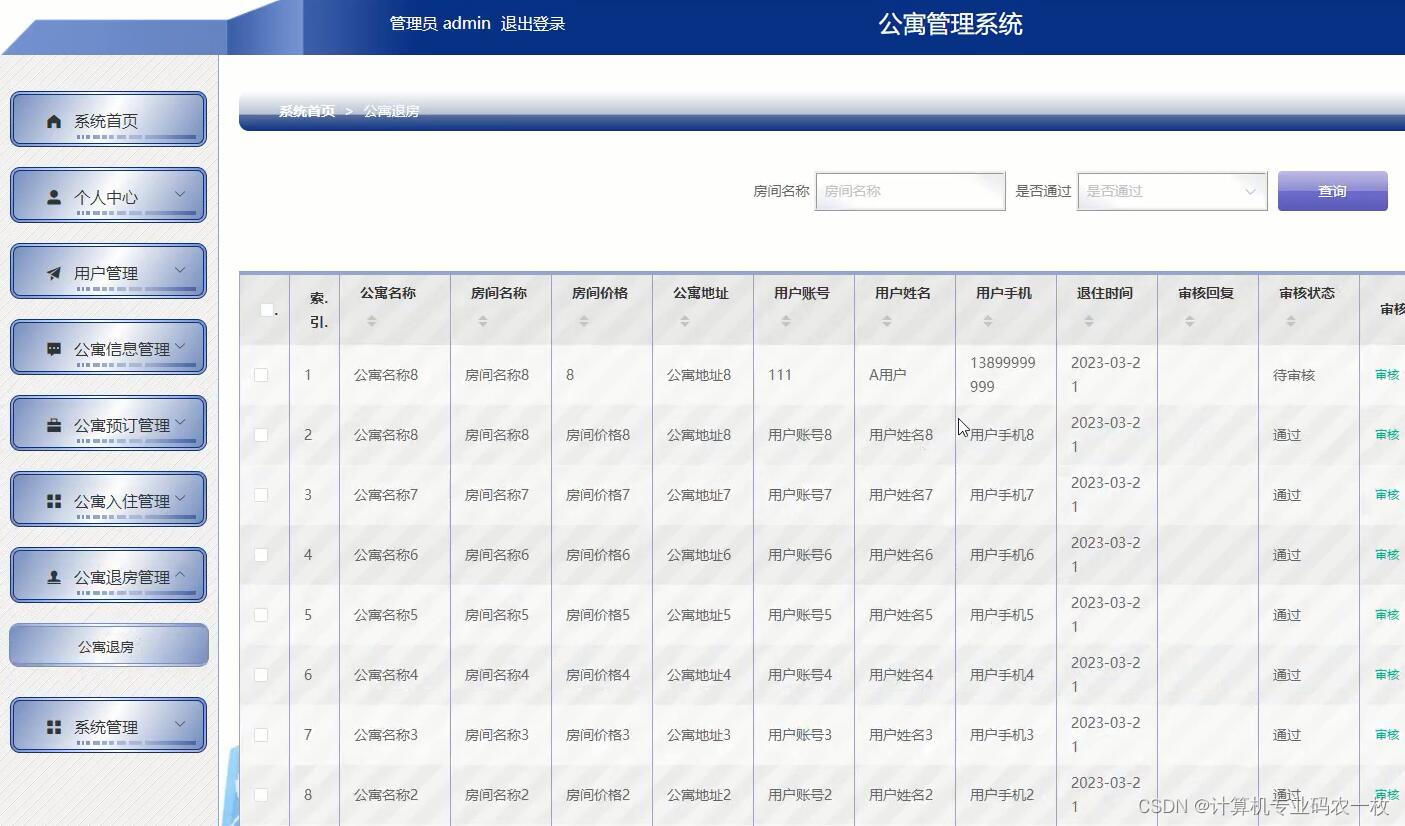
前后端分离Vue+nodejs酒店公寓客房预订管理系统udr7l-java-php-django-springboot
本系统的设计与实现共包含13个表:分别是关于我们信息表,配置文件信息表,公寓信息评论表信息表,公寓入住信息表,公寓退房信息表,公寓信息信息表,公寓预订信息表,系统公告信息表,收藏表…...

VUE打包的dist文件放到后端一起发布
背景 前后端分离开发的项目,在部署时为了方便部署,使用集成部署的方式(即前后端在一起部署的方式) 问题 直接将前端打包好的dist文件夹下的内容,放到后端项目的resource/static目录下,但是在启动访问时发…...
React入门之React_渲染基础用法和class实例写法
渲染元素 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>04元素渲染</title><script src&…...
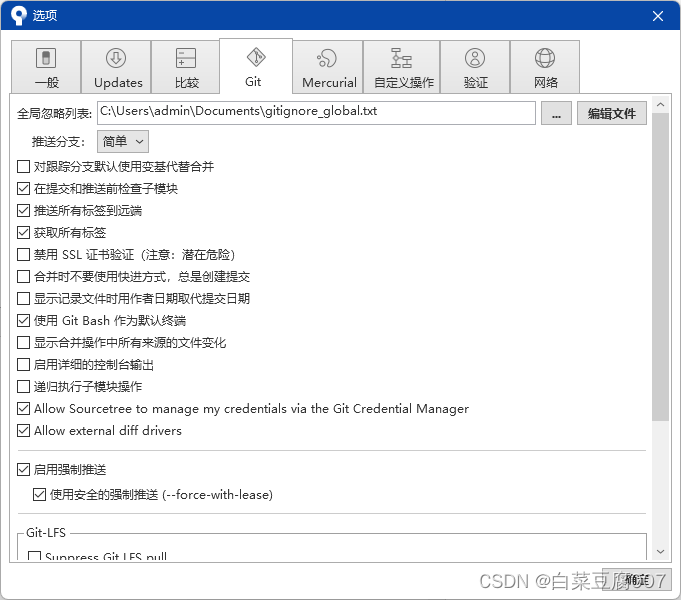
Git自动忽略dll文件的问题
检查了半天发现是sourcetreee的全局忽略文件导致, 从里面删除dll即可。 我是干脆直接删了全局忽略,太恶心了,如下: #ignore thumbnails created by windows Thumbs.db #Ignore files build by Visual Studio *.exe .vsconfig .s…...

sql中如何实现递归
在SQL中,递归通常是通过使用公用表表达式(Common Table Expressions,CTE)来实现的。CTE允许你定义一个临时的结果集,该结果集可以在一个SELECT、INSERT、UPDATE或DELETE语句的主体中被引用。 递归CTE有两个关键部分&a…...

GPT 的基础 - T(Transformer)
我们知道GPT的含义是: Generative - 生成下一个词 Pre-trained - 文本预训练 Transformer - 基于Transformer架构 我们看到Transformer模型是GPT的基础,这篇博客梳理了一下Transformer的知识点。 BERT: 用于语言理解。(Transformer的Encoder…...

微信小程序 --- 常用样式和组件
常用样式和组件 1. 组件和样式介绍 在开 Web 网站的时候: 页面的结构由 HTML 进行编写,例如:经常会用到 div、p、 span、img、a 等标签 页面的样式由 CSS 进行编写,例如:经常会采用 .class 、#id 、element 等选择…...

深圳智能制造半导体芯片行业源代码防泄密完整解决方案
一、芯片半导体行业防泄密,不能用监控及管控方式来实现,采用管控方式,首先不能主动防御,只能进行事后查询,并且管控方式,不利于嵌入式开发,对于嵌入式开发,不管是采用沙箱隔离或u口禁…...
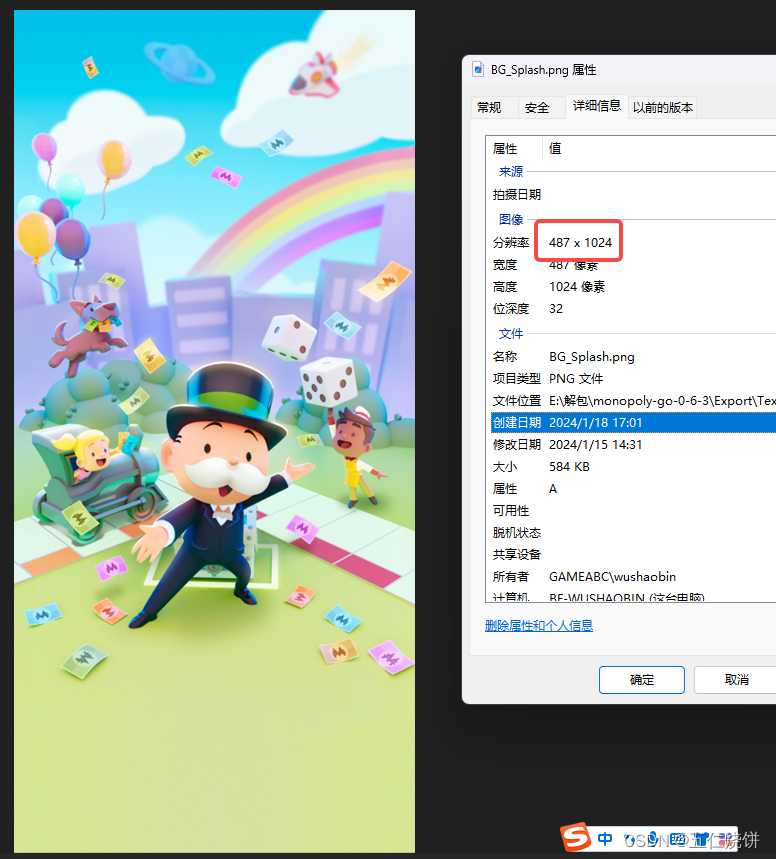
Unity UI适配规则和对热门游戏适配策略的拆解
前言 本文会介绍一些关于UI适配的基础概念,并且统计了市面上常见的设备的分辨率的情况。同时通过拆解目前市面上较为成功的两款休闲游戏Royal Match和Monopoly GO(两款均为近期游戏付费榜前几的游戏),大致推断出他们的适配策略,以供学习和参…...
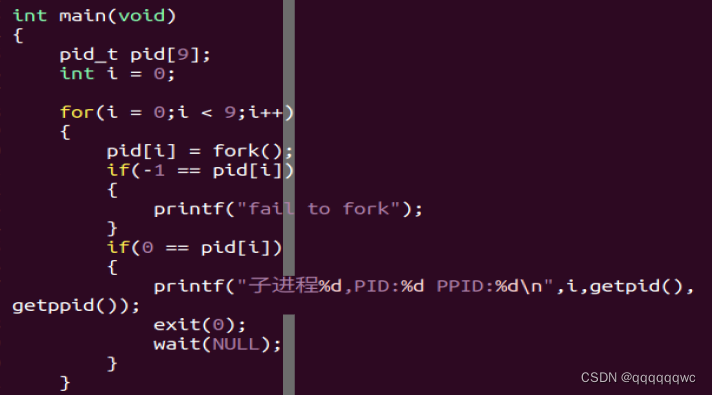
嵌入式学习day25 Linux
进程基本概念: 1.进程: 程序:存放在外存中的一段数据组成的文件 进程:是一个程序动态执行的过程,包括进程的创建、进程的调度、进程的消亡 2.进程相关命令: 1.top 动态查看当前系统中的所有进程信息(根据CPU占用率排序&a…...

Oracle数据泵跨大版本迁移数据库
Oracle数据泵跨大版本迁移数据库 source库导出元数据传输dump和数据文件到target库target库导入数据库迁移后的工作 🦈场景:将测试环境中一台Oracle 11g数据库迁移到另一台新搭建的19c数据库中。 🤔分析:由于是跨数据库大版本&…...
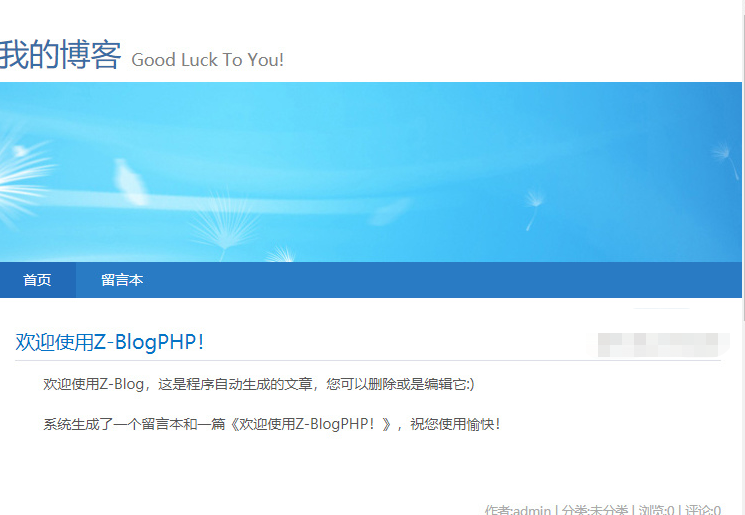
如何在Win系统从零开始搭建Z-blog网站,并将本地博客发布到公网可访问
文章目录 1. 前言2. Z-blog网站搭建2.1 XAMPP环境设置2.2 Z-blog安装2.3 Z-blog网页测试2.4 Cpolar安装和注册 3. 本地网页发布3.1. Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 想要成为一个合格的技术宅或程序员,自己搭建网站制作网页是绕…...
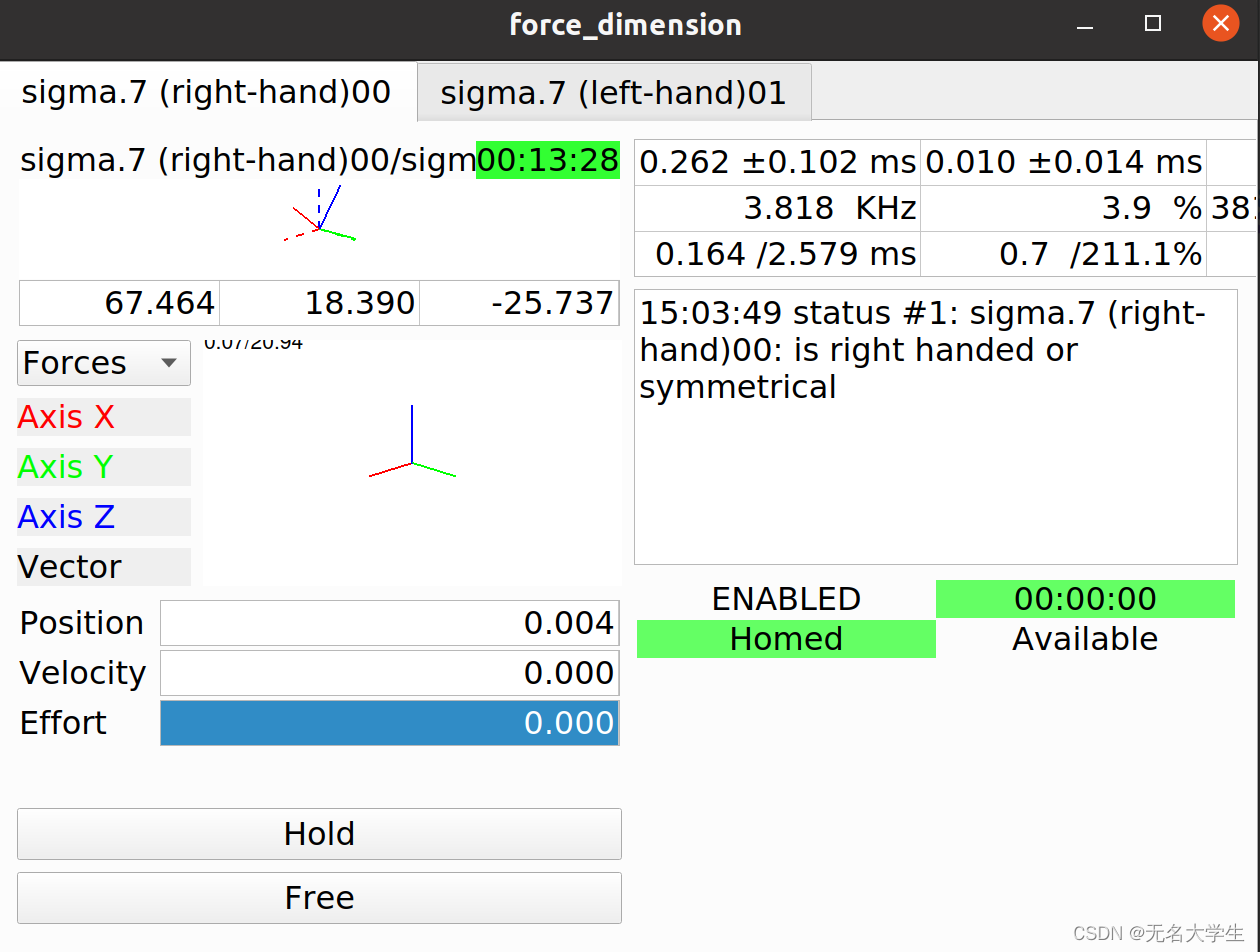
sawForceDimensionSDK安装,sigma7+ros
force dimension的sdk中没有关于ros,借助开源的sawForceDimensionSDK实现对于数据的封装和可视化,方便后续使用 链接: GitHub - jhu-saw/sawForceDimensionSDK 具体步骤: 安装qt和ros,官网下载Force Dimension SDK …...

全量知识系统问题及SmartChat给出的答复 之3
Q8. 进一步,请展示如何使用这些技术来衡量、评估或适应不可避免的不匹配的知识汤问题的更进一步的全面代码。 为了处理不可避免的不匹配的知识汤问题,我们可以引入一些技术方法来衡量、评估或适应这种情况。 下是一个更进一步的全面代码示例࿰…...

【常用的 SVN 命令及简要示例】
常用的 SVN 命令及简要示例,供您参考: 检出代码: svn checkout https://svn.example.com/project/trunk提交修改: svn commit -m "Commit message"更新代码: svn update创建分支: svn copy https://svn.example.com/project/trunk \https://sv…...
ISP代理是什么?怎么用?
在跨境出海业务中,代理IP对于您的在线任务至关重要,尤其是对于那些运行多个帐户的人来说。为您的帐户选择正确类型的代理对于确保帐户安全非常重要,劣质的IP容易使账号遭受封号风险。IPFoxy的多种代理IP类型应用范围各有侧重,其中…...
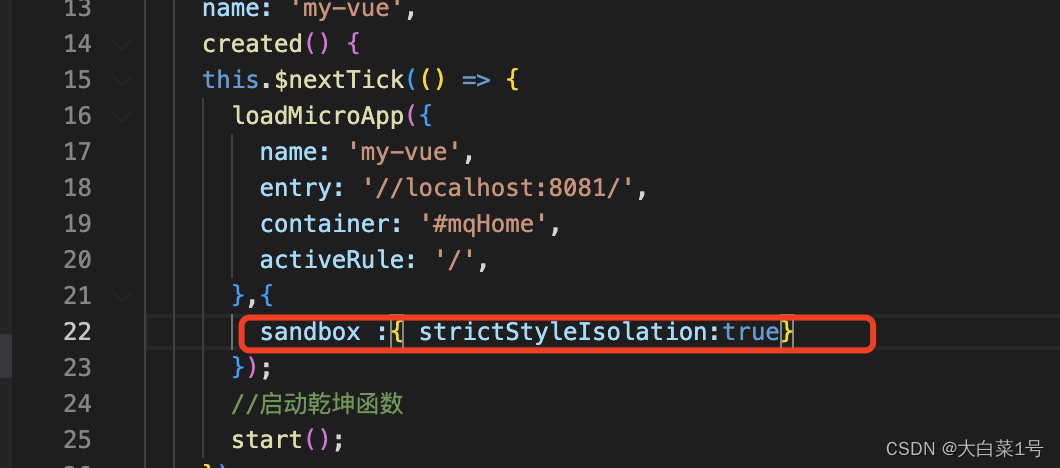
微服务之qiankun主项目+子项目搭建
主项目使用history,子项目使用hash模式 1. 下载安装"qiankun": "^2.10.13"2. 手动调用qiankun,使用vue脚手架搭建的项目1. 主项目配置(我使用的是手动调用乾坤,在指定页面显示内容)1. 要使用的页面中引入乾坤…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
