matlab:涉及复杂函数图像的交点求解
matlab:涉及复杂函数图像的交点求解
在MATLAB中求解两个图像的交点是一个常见的需求。本文将通过一个示例,展示如何求解两个图像的交点,并提供相应的MATLAB代码。
画出图像
首先,我们需要绘制两个图像,以便直观地看到它们的交点。以下是绘制图像的MATLAB代码:
% 定义符号变量
syms x1 x2;% 上边界方程
eq1 = 10 + 110 * (0.8 + 0.05 + 0.4 * sin(4 * atan2(x2, x1))^16)^2 - (x1 + x2) == 0;% 绘制图形
figure;% 使用 fimplicit 绘制上边界
fimplicit(@(x1, x2) 10 + 110 * (b + 0.05 + 0.4 * sin(4 * atan2(x2, x1))^16)^2 - (x1 + x2), [0, 100, 0, 100]);
hold on;% 使用 fimplicit 绘制 y = 100 - x1
fimplicit(@(x1, x2) x1 + x2 - 100, [0, 100, 0, 100]);% 设置图例和标题
legend('Upper Boundary', 'y = 100 - x1');
title('Plot of Equations');
xlabel('x1');
ylabel('x2');
hold off;
绘制的图像如下所示:
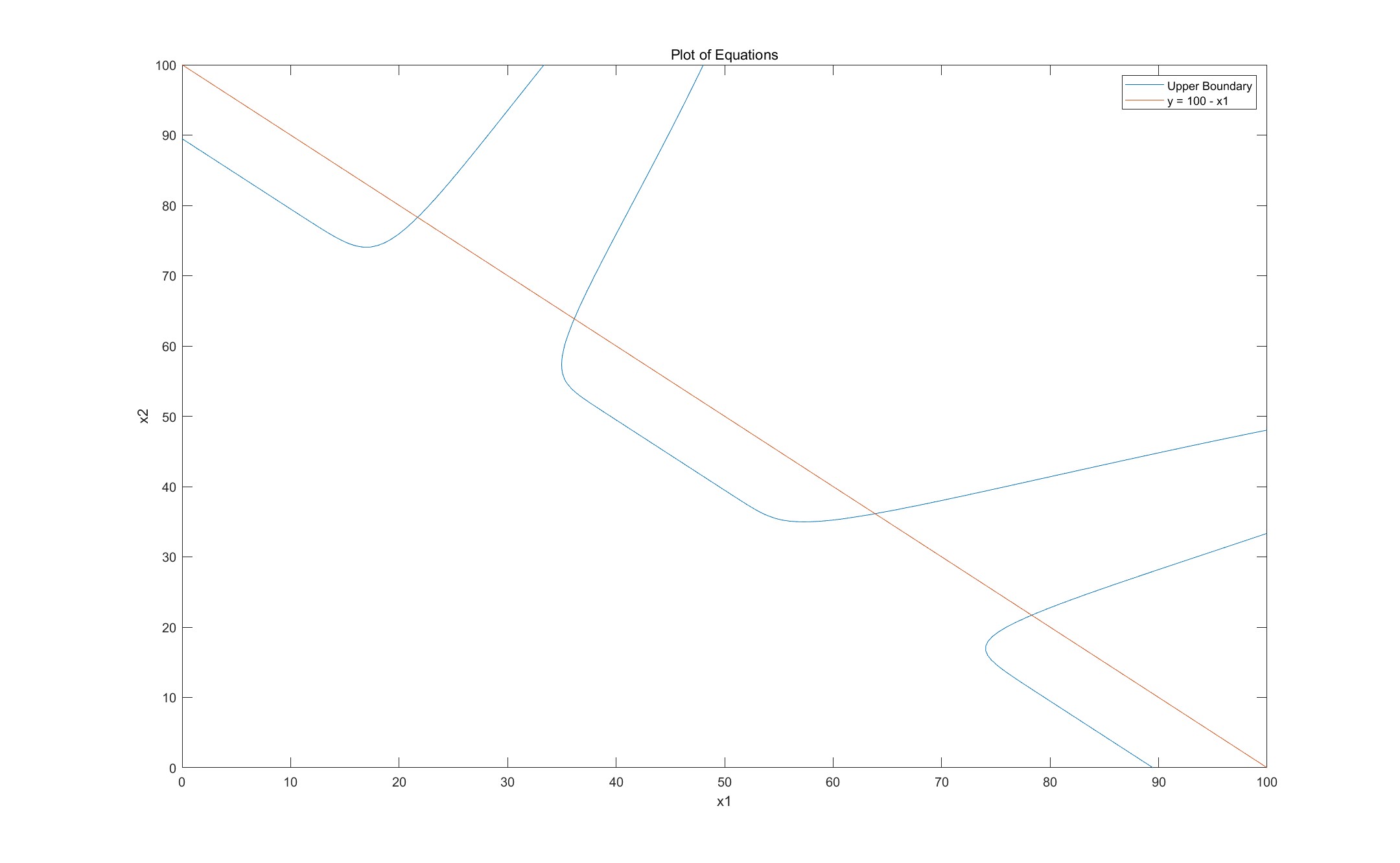
从图中可以看出,存在四个实数域交点。
求解交点方法1:solve不加求解范围(失败)
首先尝试使用solve函数来求解交点:
% 定义符号变量
syms x1 x2;% 定义参数
b = 0.8;
l = atan2(x2, x1);% 定义方程组
eq1 = 10 + 110 * (b + 0.05 + 0.4 * sin(4 * l)^16)^2 - (x1 + x2);
eq2 = x1 + x2 - 100;% 解方程组
[sol_x1, sol_x2] = solve([eq1 == 0, eq2 == 0], [x1, x2]);% 转换为数值解
sol_x1 = double(sol_x1);
sol_x2 = double(sol_x2);% 筛选实数解
real_solutions = [sol_x1, sol_x2];
real_solutions = real_solutions(imag(real_solutions(:, 1)) == 0 & imag(real_solutions(:, 2)) == 0, :);% 输出实数解
disp('Real solutions (x1, x2):');
disp(real_solutions);
输出为空值,这表明在解的过程中遇到了问题。
求解交点方法2:solve加求解范围(成功)
% 定义符号变量
syms x1 x2;% 求解范围
assume(x1>=0&x1<=100)
assume(x2>=0&x2<=100)% 定义参数
b = 0.8;
l = atan2(x2, x1);% 定义方程组
eq1 = 10 + 110 * (b + 0.05 + 0.4 * sin(4 * l)^16)^2 - (x1 + x2);
eq2 = x1 + x2 - 100;% 解方程组
[sol_x1, sol_x2] = solve([eq1 == 0, eq2 == 0], [x1, x2]);% 转换为数值解
sol_x1 = double(sol_x1);
sol_x2 = double(sol_x2);% 筛选实数解
real_solutions = [sol_x1, sol_x2];
real_solutions = real_solutions(imag(real_solutions(:, 1)) == 0 & imag(real_solutions(:, 2)) == 0, :);% 输出实数解
disp('Real solutions (x1, x2):');
disp(real_solutions);
输出:

求解交点方法3:fsolve(成功)
下面通过数值方法而不是符号方法来找到解,使用 fsolve(数值求解函数):
% 定义匿名函数
func = @(x) [10 + 110 * (b + 0.05 + 0.4 * sin(4 * atan2(x(2), x(1)))^16)^2 - (x(1) + x(2)), x(1) + x(2) - 100];% 设置选项以使用较大的初始搜索范围
options = optimoptions('fsolve', 'Display', 'off', 'MaxFunctionEvaluations', 6000, 'MaxIterations', 4000);% 存储解
solutions = [];% 尝试多个随机初始猜测
for i = 1:100initial_guess = rand(1, 2) * 100; % 生成0到100之间的随机初始猜测[sol, fval, exitflag, output] = fsolve(func, initial_guess, options);% 只有当fsolve成功收敛时才记录解if exitflag > 0 && all(abs(fval) < 1e-6)solutions = [solutions; sol];end
end% 去除重复的解,考虑数值误差
solutions = round(solutions, 3); % 四舍五入到三位小数
solutions = unique(solutions, 'rows', 'stable');% 过滤掉不在感兴趣区域的解
solutions = solutions(all(solutions >= 0 & solutions <= 100, 2), :);% 输出数值解
disp('Numerical solutions (x1, x2):');
disp(solutions);
输出:

这表明成功找到了交点的坐标,不过误差稍大一些。
总结
- 使用solve时,限制求解范围是重要的
- 当solve无能为力的时候,可以试试fsolve
相关文章:

matlab:涉及复杂函数图像的交点求解
matlab:涉及复杂函数图像的交点求解 在MATLAB中求解两个图像的交点是一个常见的需求。本文将通过一个示例,展示如何求解两个图像的交点,并提供相应的MATLAB代码。 画出图像 首先,我们需要绘制两个图像,以便直观地看…...
Unity(第二十二部)官方的反向动力学一般使用商城的IK插件,这个用的不多
反向动力学(Inverse Kinematic,简称IK)是一种通过子节点带动父节点运动的方法。 正向动力学 在骨骼动画中,大多数动画是通过将骨架中的关节角度旋转到预定值来生成的,子关节的位置根据父关节的旋转而改变,这…...

nginx反向代理,获取客户端ip
一、获取客户端ip代码 /*** description: 获取客户端IP* return string*/ public static function getClientIp(){$ip ;if(getenv(HTTP_CLIENT_IP) && strcasecmp(getenv(HTTP_CLIENT_IP),unknown)){$ip getenv(HTTP_CLIENT_IP);}else if(getenv(HTTP_X_FORWARDED_F…...
G. The Morning Star(简单容斥))
13 Codeforces Round 886 (Div. 4)G. The Morning Star(简单容斥)
G. The Morning Star 思路:用map记录x,y,以及y-x、yx从前往后统计一遍答案即可公式 a n s c n t [ x ] c n t [ y ] − 2 ∗ c n t [ x , y ] c n t [ y x ] c n t [ y − x ] anscnt[x]cnt[y]-2 * cnt[x,y]cnt[yx]cnt[y-x] anscnt[x]…...

CLion 2023:专注于C和C++编程的智能IDE mac/win版
JetBrains CLion 2023是一款专为C和C开发者设计的集成开发环境(IDE),它集成了许多先进的功能,旨在提高开发效率和生产力。 CLion 2023软件获取 CLion 2023的智能代码编辑器提供了丰富的代码补全和提示功能,使您能够更…...
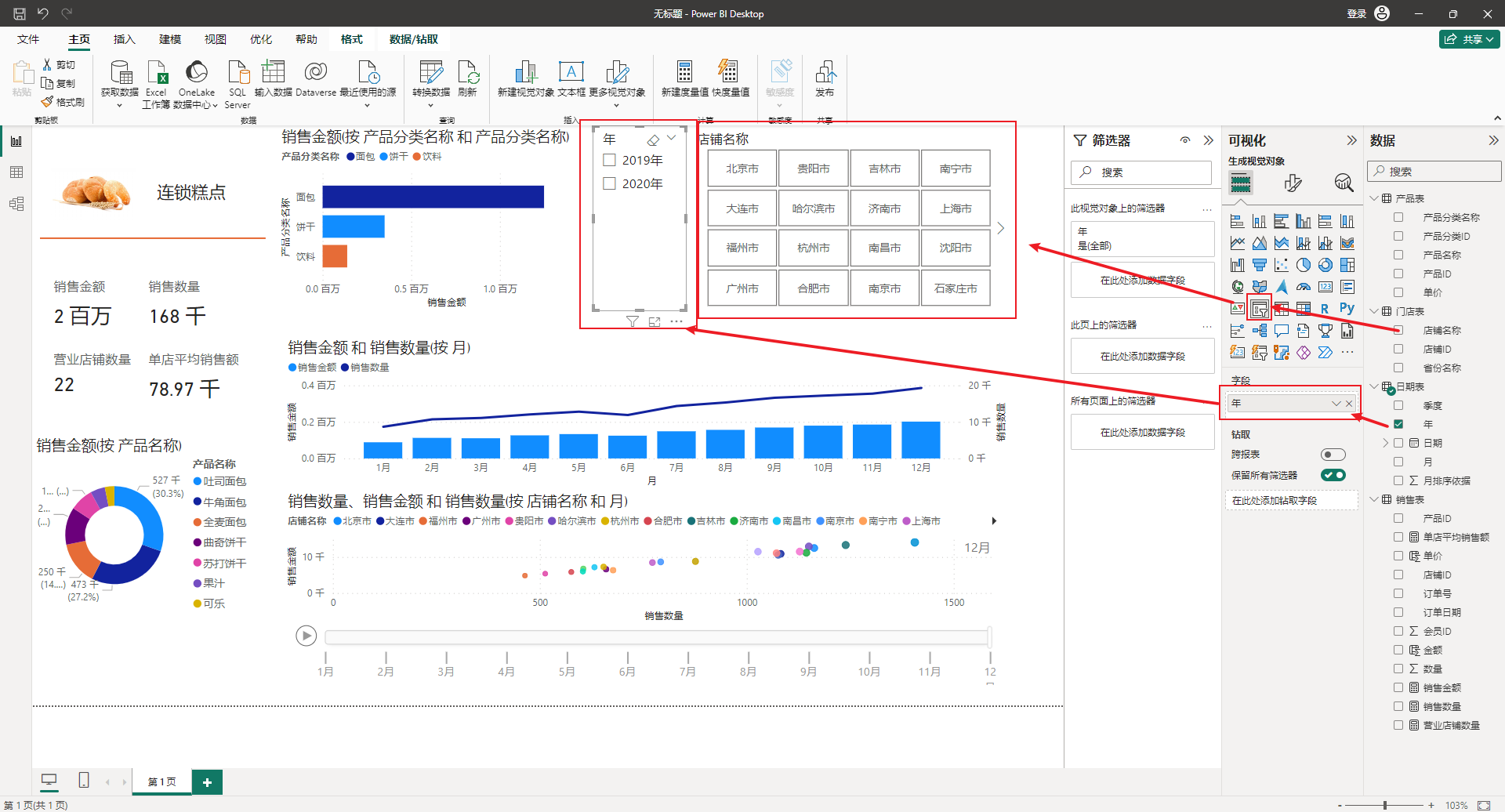
数据可视化基础与应用-02-基于powerbi实现连锁糕点店数据集的仪表盘制作
总结 本系列是数据可视化基础与应用的第02篇,主要介绍基于powerbi实现一个连锁糕点店数据集的仪表盘制作。 数据集描述 有一个数据集,包含四张工作簿,每个工作簿是一张表,其中可以销售表可以划分为事实表,产品表&am…...
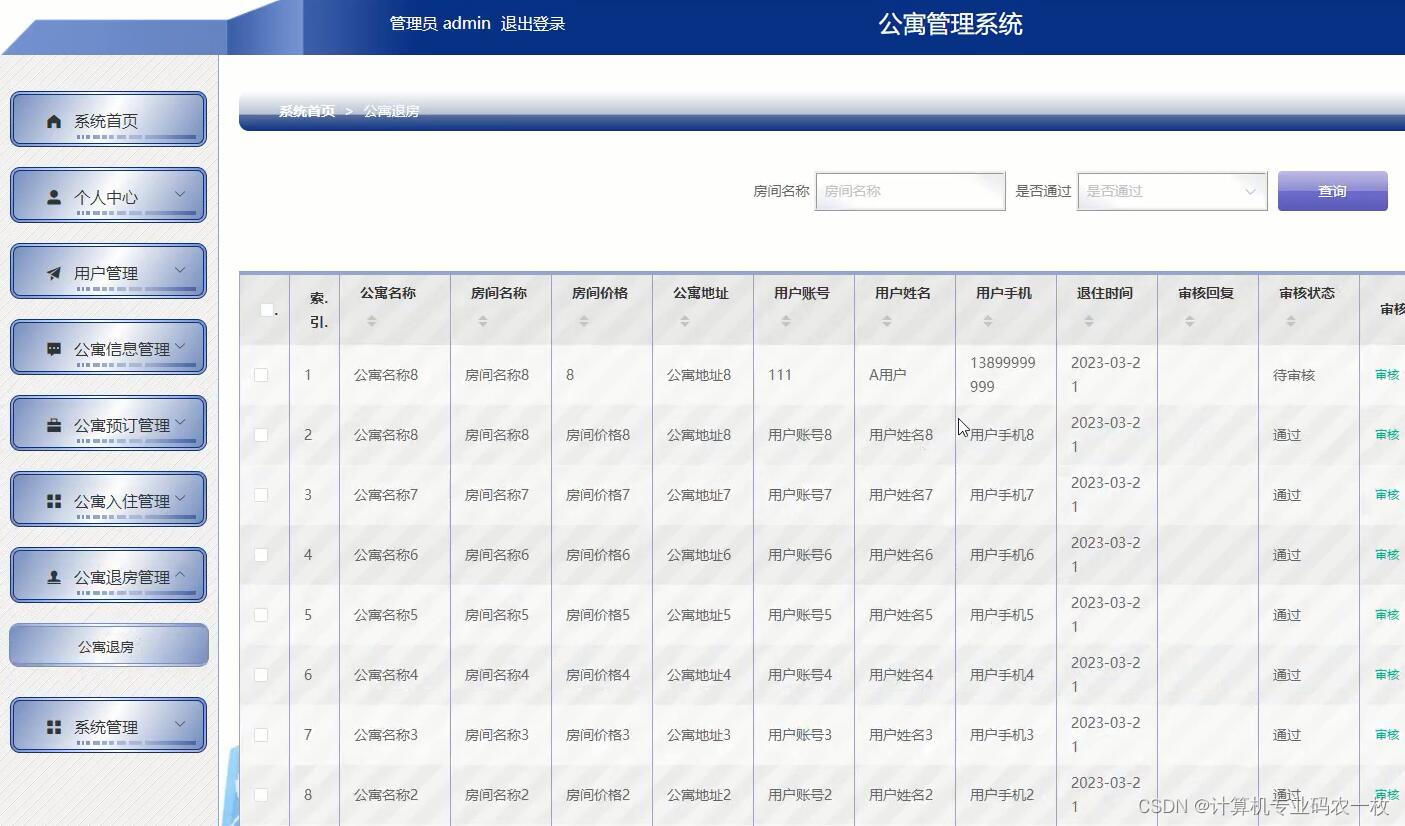
前后端分离Vue+nodejs酒店公寓客房预订管理系统udr7l-java-php-django-springboot
本系统的设计与实现共包含13个表:分别是关于我们信息表,配置文件信息表,公寓信息评论表信息表,公寓入住信息表,公寓退房信息表,公寓信息信息表,公寓预订信息表,系统公告信息表,收藏表…...

VUE打包的dist文件放到后端一起发布
背景 前后端分离开发的项目,在部署时为了方便部署,使用集成部署的方式(即前后端在一起部署的方式) 问题 直接将前端打包好的dist文件夹下的内容,放到后端项目的resource/static目录下,但是在启动访问时发…...
React入门之React_渲染基础用法和class实例写法
渲染元素 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>04元素渲染</title><script src&…...
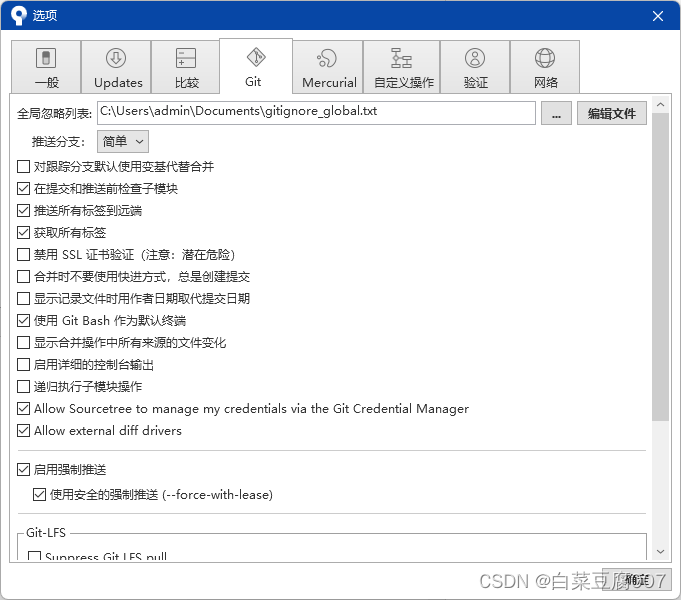
Git自动忽略dll文件的问题
检查了半天发现是sourcetreee的全局忽略文件导致, 从里面删除dll即可。 我是干脆直接删了全局忽略,太恶心了,如下: #ignore thumbnails created by windows Thumbs.db #Ignore files build by Visual Studio *.exe .vsconfig .s…...

sql中如何实现递归
在SQL中,递归通常是通过使用公用表表达式(Common Table Expressions,CTE)来实现的。CTE允许你定义一个临时的结果集,该结果集可以在一个SELECT、INSERT、UPDATE或DELETE语句的主体中被引用。 递归CTE有两个关键部分&a…...

GPT 的基础 - T(Transformer)
我们知道GPT的含义是: Generative - 生成下一个词 Pre-trained - 文本预训练 Transformer - 基于Transformer架构 我们看到Transformer模型是GPT的基础,这篇博客梳理了一下Transformer的知识点。 BERT: 用于语言理解。(Transformer的Encoder…...

微信小程序 --- 常用样式和组件
常用样式和组件 1. 组件和样式介绍 在开 Web 网站的时候: 页面的结构由 HTML 进行编写,例如:经常会用到 div、p、 span、img、a 等标签 页面的样式由 CSS 进行编写,例如:经常会采用 .class 、#id 、element 等选择…...

深圳智能制造半导体芯片行业源代码防泄密完整解决方案
一、芯片半导体行业防泄密,不能用监控及管控方式来实现,采用管控方式,首先不能主动防御,只能进行事后查询,并且管控方式,不利于嵌入式开发,对于嵌入式开发,不管是采用沙箱隔离或u口禁…...
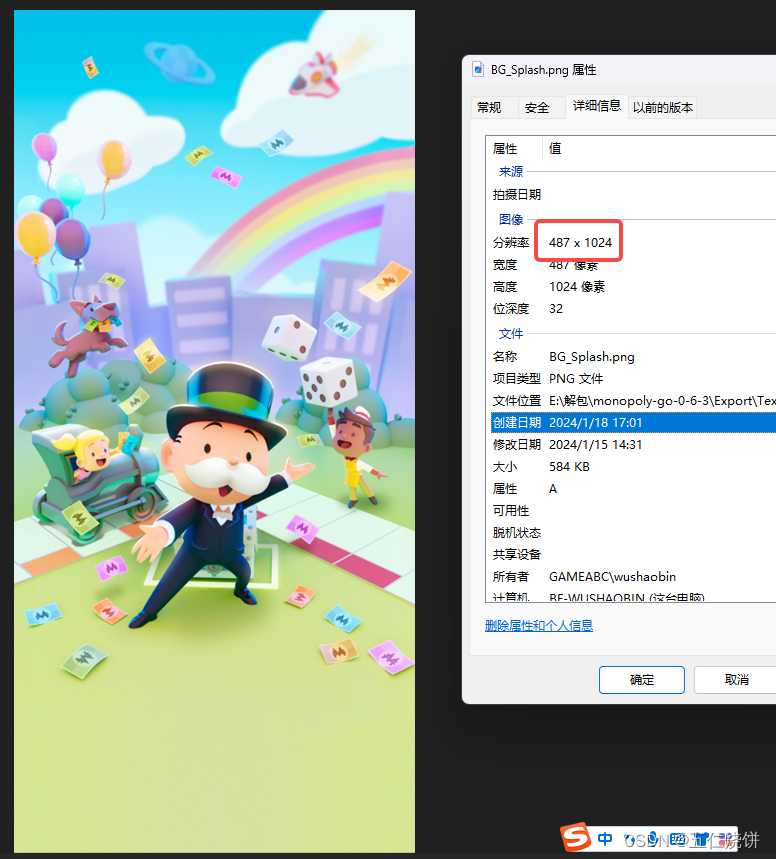
Unity UI适配规则和对热门游戏适配策略的拆解
前言 本文会介绍一些关于UI适配的基础概念,并且统计了市面上常见的设备的分辨率的情况。同时通过拆解目前市面上较为成功的两款休闲游戏Royal Match和Monopoly GO(两款均为近期游戏付费榜前几的游戏),大致推断出他们的适配策略,以供学习和参…...
嵌入式学习day25 Linux
进程基本概念: 1.进程: 程序:存放在外存中的一段数据组成的文件 进程:是一个程序动态执行的过程,包括进程的创建、进程的调度、进程的消亡 2.进程相关命令: 1.top 动态查看当前系统中的所有进程信息(根据CPU占用率排序&a…...

Oracle数据泵跨大版本迁移数据库
Oracle数据泵跨大版本迁移数据库 source库导出元数据传输dump和数据文件到target库target库导入数据库迁移后的工作 🦈场景:将测试环境中一台Oracle 11g数据库迁移到另一台新搭建的19c数据库中。 🤔分析:由于是跨数据库大版本&…...
如何在Win系统从零开始搭建Z-blog网站,并将本地博客发布到公网可访问
文章目录 1. 前言2. Z-blog网站搭建2.1 XAMPP环境设置2.2 Z-blog安装2.3 Z-blog网页测试2.4 Cpolar安装和注册 3. 本地网页发布3.1. Cpolar云端设置3.2 Cpolar本地设置 4. 公网访问测试5. 结语 1. 前言 想要成为一个合格的技术宅或程序员,自己搭建网站制作网页是绕…...
sawForceDimensionSDK安装,sigma7+ros
force dimension的sdk中没有关于ros,借助开源的sawForceDimensionSDK实现对于数据的封装和可视化,方便后续使用 链接: GitHub - jhu-saw/sawForceDimensionSDK 具体步骤: 安装qt和ros,官网下载Force Dimension SDK …...

全量知识系统问题及SmartChat给出的答复 之3
Q8. 进一步,请展示如何使用这些技术来衡量、评估或适应不可避免的不匹配的知识汤问题的更进一步的全面代码。 为了处理不可避免的不匹配的知识汤问题,我们可以引入一些技术方法来衡量、评估或适应这种情况。 下是一个更进一步的全面代码示例࿰…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
