蓝桥杯:真题讲解3(C++版)附带解析
报纸页数
来自:2016年七届省赛大学C组真题(共8道题)

分析: --画出报纸长的样子,如果我们在上面多画一张报纸,那么就符合题意的5,6,11,12。
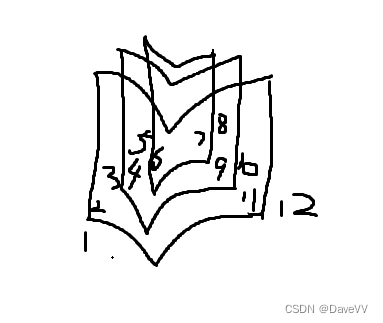
观察这张图:观察3,4,9,10这一张报纸,怎么求出这份报纸一共多少页呢?
3+10=13 再用13-1就是这份报纸一共有的页数。
公式:(最小页码+最大页码-1)
代码:
#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码cout << 1125+1728-1;return 0;
}等差素数列
来自:2017年八届省赛大学B组真题(共8道题)

分析:
拓展一个知识:
长度为k的素数等差数列,它的公差d能被小于k的所有素数整除。
由上可知,长度为k的素数等差数列的最小公差为小于k的所有素数之积。
10以内的素数为2,3,5,7,所以2*3*5*7=210。
代码:
#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码cout << 210;return 0;
}乘积尾零
来自:2018年九届省赛大学B组真题(共8道题)
分析:
乘积出现尾零,肯定是5和偶数相乘得到的,每出现一个10,就应从乘数中可以提出一个2、一个5。所以我们把每个数的都分解成乘积的形式 ,统计出2和5的数量,然后取较小那个。
(可以举100*10的例子来推一下)
代码:
#include <bits/stdc++.h>
using namespace std;
int main() {// 请在此输入您的代码int cnt2=0,cnt5=0; //统计数的,要初始化为0int a[100];for(int i=0; i<=99; i++) {cin >> a[i];while(a[i]%2==0) {cnt2++;a[i]/=2;}while(a[i]%5==0) {cnt5++;a[i]/=5;}}cout << min(cnt2,cnt5);return 0;
}次数差
来自:2018年九届省赛大学C组真题(共6道题)
 +
+
代码(分析在注释中):
#include <bits/stdc++.h>
using namespace std;
int main() {// 请在此输入您的代码string str;cin >> str;int arr[26]= {0}; //全部初始化为0for(int i=0; i<(int)str.size(); i++) {//对于size函数来说,返回一个int或一个unsigned似乎都是合理的。但其实size函数返回的是一个string::size_type类型的值。arr[str[i]-'a']++;}sort(arr,arr+26);for(int i=0; i<26; i++) { //为什么要套一个for循环?因为有可能有的球队一次也没赢,题目中写了不关心那些一次也没获胜的。//并且我们也是按哪个队获胜,然后放到相应的位置,有的位置根本没有相应的++操作。if(arr[i]!=0) {cout << arr[25]-arr[i] << endl;break;}}return 0;
}猴子分香蕉
来自:2018年九届省赛大学C组真题(共6道题)

分析:因为是填空题,直接暴力求解即可。
代码:
#include <iostream>
using namespace std;
int main() {// 请在此输入您的代码for(int i=1; i<=10000; i++) {int p=i;if(p%5==1) {p=p-p/5-1;if(p%5==2) {p=p-p/5-2;if(p%5==3) {p=p-p/5-3;if(p%5==4) {p=p-p/5-4;if(p%5==0 && p>0) { //这一步要加p >0 ,上面不需要加,上面不符合if判断直接跳下一层循环了 cout << i;return 0;}}}}}}return 0;
}相关文章:

蓝桥杯:真题讲解3(C++版)附带解析
报纸页数 来自:2016年七届省赛大学C组真题(共8道题) 分析: --画出报纸长的样子,如果我们在上面多画一张报纸,那么就符合题意的5,6,11,12。 观察这张图:观察3…...
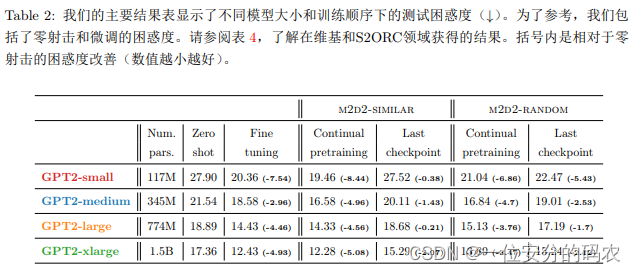
继续预训练对大语言模型的影响
翻译自文章:Investigating Continual Pretraining in Large Language Models: Insights and Implications 摘要 本文研究了大型语言模型(LLMs)中不断学习(CL)的不断发展领域,重点是制定有效和可持续的训练…...

关于空频变换的知识点
1.DCT变换: 离散余弦变换是一种将图像从空域转换到频域的技术,它可以将图像分解为频域分量。对于RGB图像,它由红色(R)、绿色(G)和蓝色(B)三个通道组成。当应用DCT变换时…...

纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐
纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐 使用flex实现 思路 容器样式(.container): Flex容器的BFC性质使得其内部的子元素(.text-box)在水平方向上能够居中,通过justify-c…...
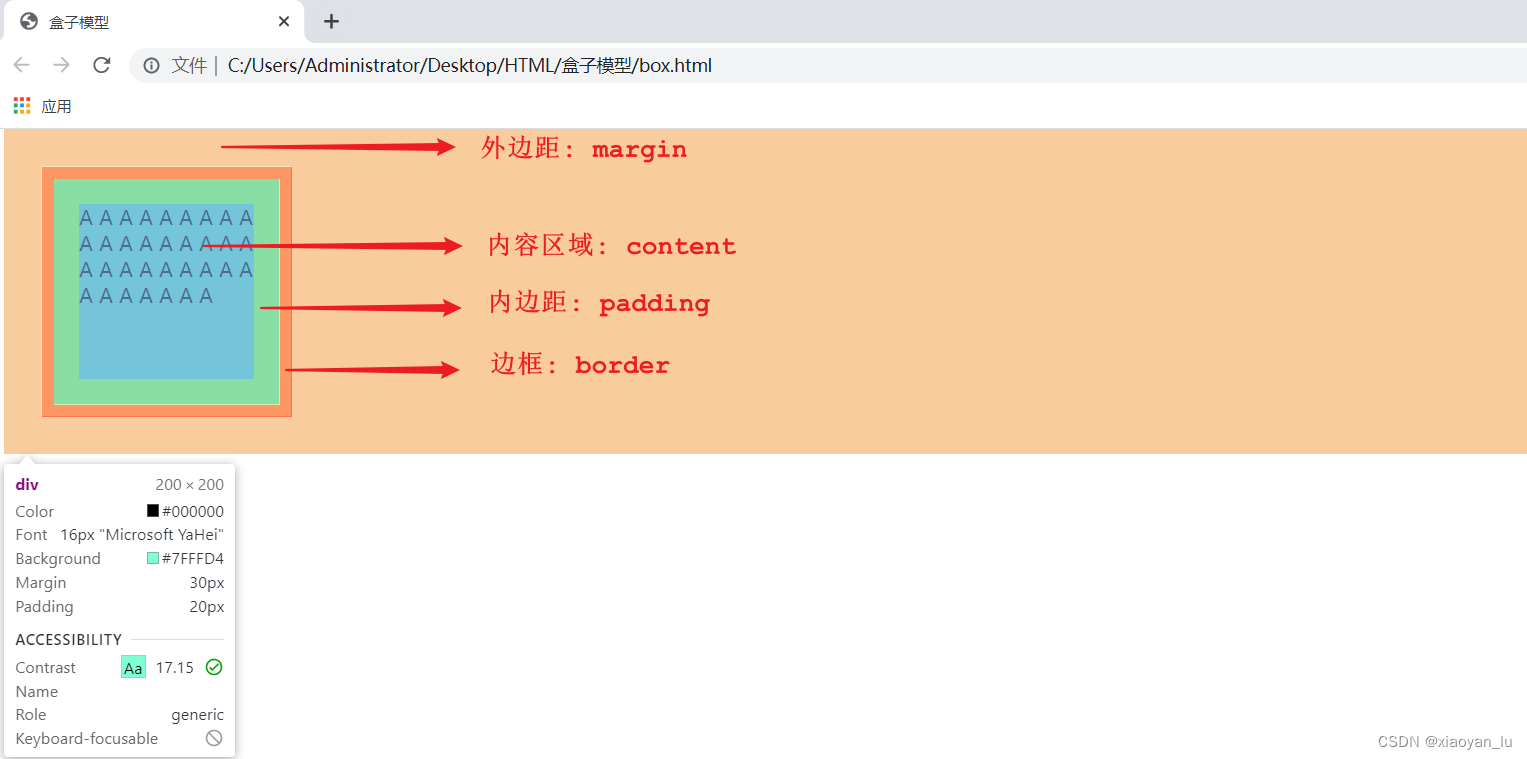
初学HTMLCSS——盒子模型
盒子模型 盒子:页面中所有的元素(标签),都可以看做是一个 盒子,由盒子将页面中的元素包含在一个矩形区域内,通过盒子的视角更方便的进行页面布局盒子模型组成:内容区域(content&…...
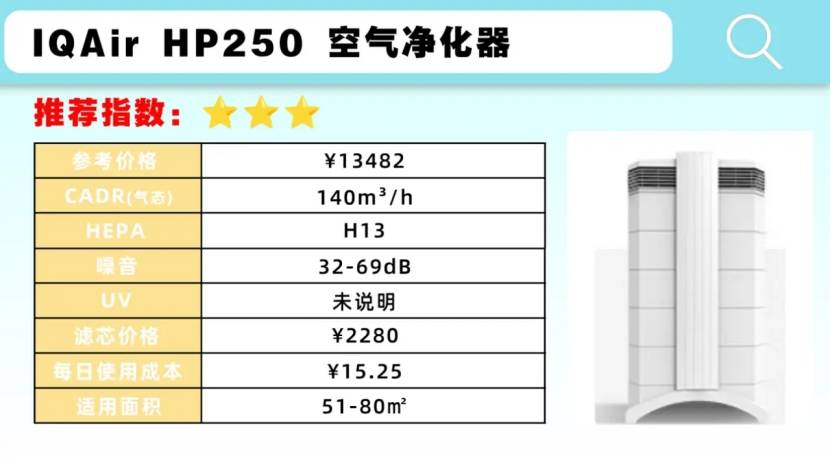
吸猫毛空气净化器哪个好?推荐除猫毛好的宠物空气净化器品牌
如今,越来越多的家庭选择养宠物!虽然家里变得更加温馨,但养宠可能会带来异味和空气中的毛发增多可能会引发健康问题,这也是一个大问题。 但我不想家里到处都是异味,尤其是便便的味道,所以很需要一款能够处…...

【玩转408数据结构】线性表——双链表、循环链表和静态链表(线性表的链式表示 下)
知识回顾 在前面的学习中,我们已经了解到了链表(线性表的链式存储)的一些基本特点,并且深入的研究探讨了单链表的一些特性,我们知道,单链表在实现插入删除上,是要比顺序表方便的,但是…...
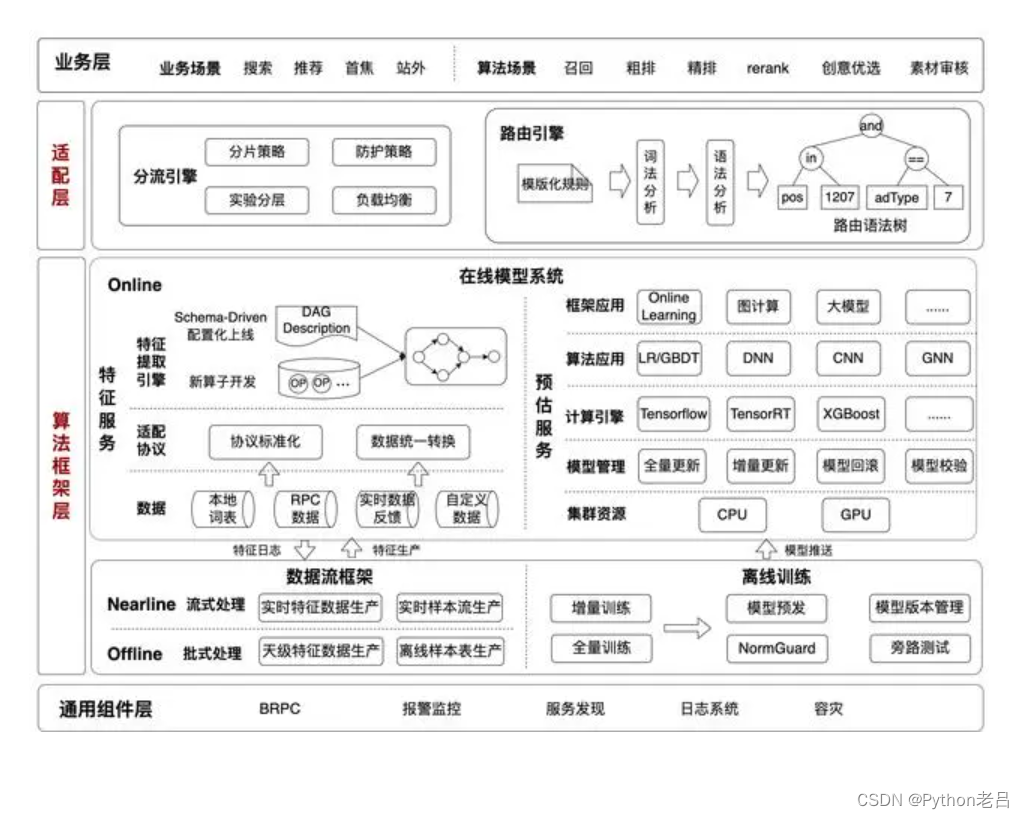
分布式概念
分布式概念 一、分布式介绍1.1 分布式计算1.1.1 分布式计算的方法1.1.1 分布式计算与互联网的普及1.1.2 分布式计算项目1.1.3 参与计算 1.2 分布式存储系统1.2.1 P2P 数据存储系统1.2.2 云存储系统 1.3 应用 二、分布式基础概念2.1 微服务2.2 集群2.3 分布式2.4 节点2.5 远程调…...

vue中的ref/reactive区别及原理
Vue中的ref和reactive是两种不同的数据响应式管理方式。 ref是Vue 3中新加入的特性,它可以将一个普通的JavaScript对象转换为响应式对象。通过ref创建的响应式对象在访问和修改时会自动触发重新渲染。ref返回的是一个包含value属性的对象,访问或修改数据…...
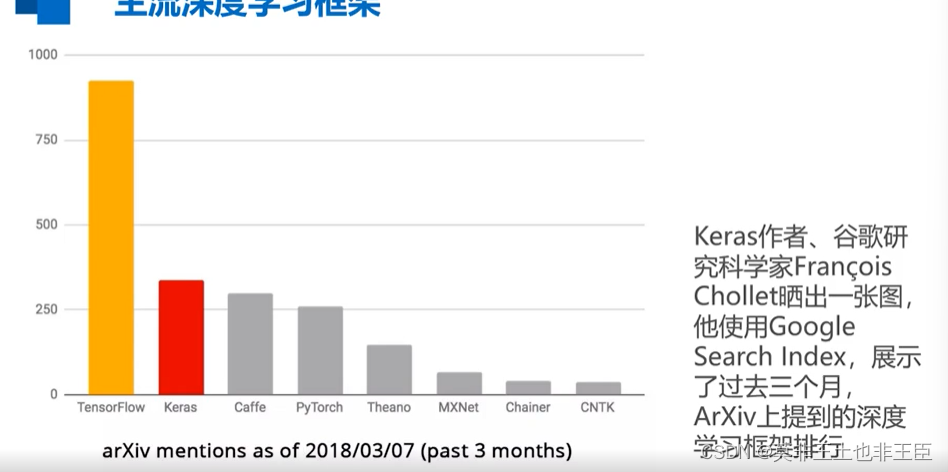
深度学习介绍与环境搭建
深度学习介绍与环境搭建 慕课大学人工智能学习笔记,自己学习记录用的。(赋上连接) https://www.icourse163.org/learn/ZUCC-1206146808?tid1471365447#/learn/content?typedetail&id1256424053&cid1289366515人工智能、机器学习与…...
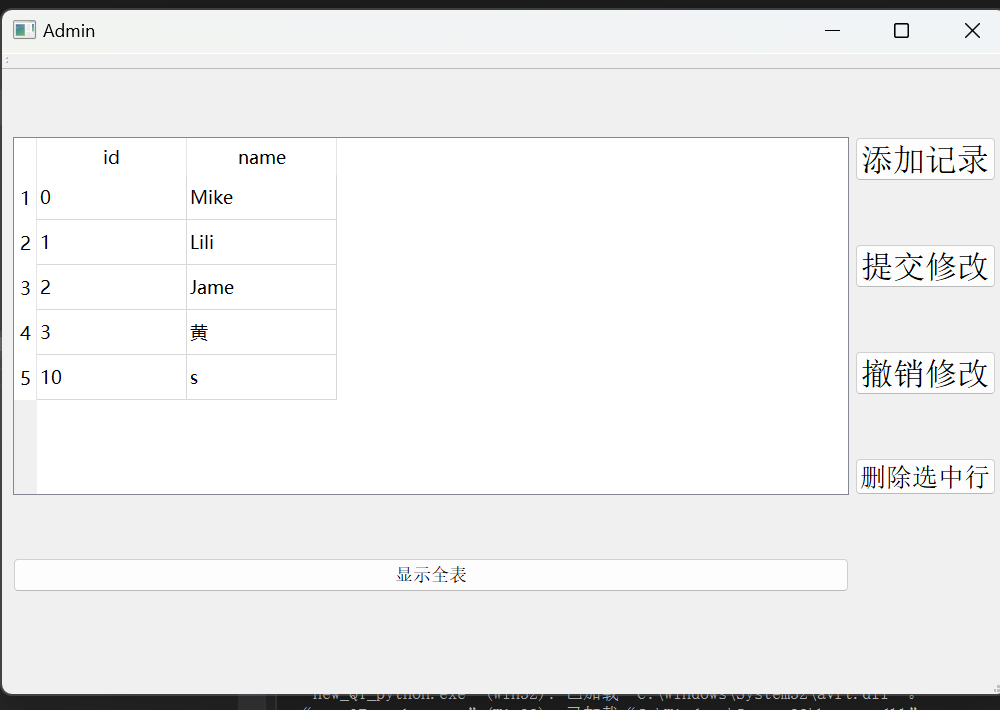
QT C++实践|超详细数据库的连接和增删改查操作|附源码
0:前言 🪧 什么情况需要数据库? 1 大规模的数据需要处理(比如上千上万的数据量)2 需要把数据信息存储起来,无论是本地还是服务上,而不是断电后数据信息就消失了。 如果不是上面的原因化,一般…...

matlab:涉及复杂函数图像的交点求解
matlab:涉及复杂函数图像的交点求解 在MATLAB中求解两个图像的交点是一个常见的需求。本文将通过一个示例,展示如何求解两个图像的交点,并提供相应的MATLAB代码。 画出图像 首先,我们需要绘制两个图像,以便直观地看…...
Unity(第二十二部)官方的反向动力学一般使用商城的IK插件,这个用的不多
反向动力学(Inverse Kinematic,简称IK)是一种通过子节点带动父节点运动的方法。 正向动力学 在骨骼动画中,大多数动画是通过将骨架中的关节角度旋转到预定值来生成的,子关节的位置根据父关节的旋转而改变,这…...

nginx反向代理,获取客户端ip
一、获取客户端ip代码 /*** description: 获取客户端IP* return string*/ public static function getClientIp(){$ip ;if(getenv(HTTP_CLIENT_IP) && strcasecmp(getenv(HTTP_CLIENT_IP),unknown)){$ip getenv(HTTP_CLIENT_IP);}else if(getenv(HTTP_X_FORWARDED_F…...
G. The Morning Star(简单容斥))
13 Codeforces Round 886 (Div. 4)G. The Morning Star(简单容斥)
G. The Morning Star 思路:用map记录x,y,以及y-x、yx从前往后统计一遍答案即可公式 a n s c n t [ x ] c n t [ y ] − 2 ∗ c n t [ x , y ] c n t [ y x ] c n t [ y − x ] anscnt[x]cnt[y]-2 * cnt[x,y]cnt[yx]cnt[y-x] anscnt[x]…...

CLion 2023:专注于C和C++编程的智能IDE mac/win版
JetBrains CLion 2023是一款专为C和C开发者设计的集成开发环境(IDE),它集成了许多先进的功能,旨在提高开发效率和生产力。 CLion 2023软件获取 CLion 2023的智能代码编辑器提供了丰富的代码补全和提示功能,使您能够更…...
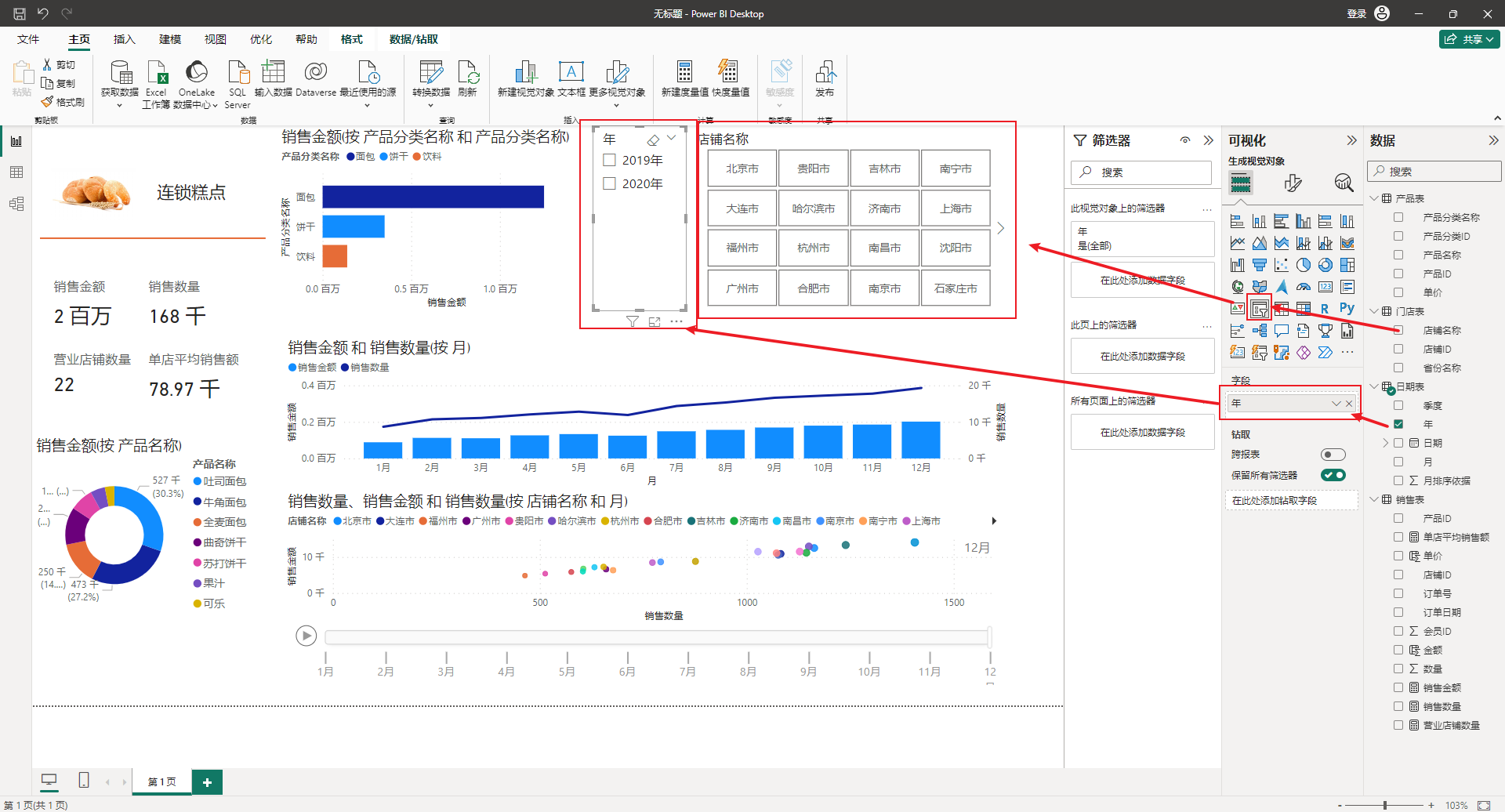
数据可视化基础与应用-02-基于powerbi实现连锁糕点店数据集的仪表盘制作
总结 本系列是数据可视化基础与应用的第02篇,主要介绍基于powerbi实现一个连锁糕点店数据集的仪表盘制作。 数据集描述 有一个数据集,包含四张工作簿,每个工作簿是一张表,其中可以销售表可以划分为事实表,产品表&am…...
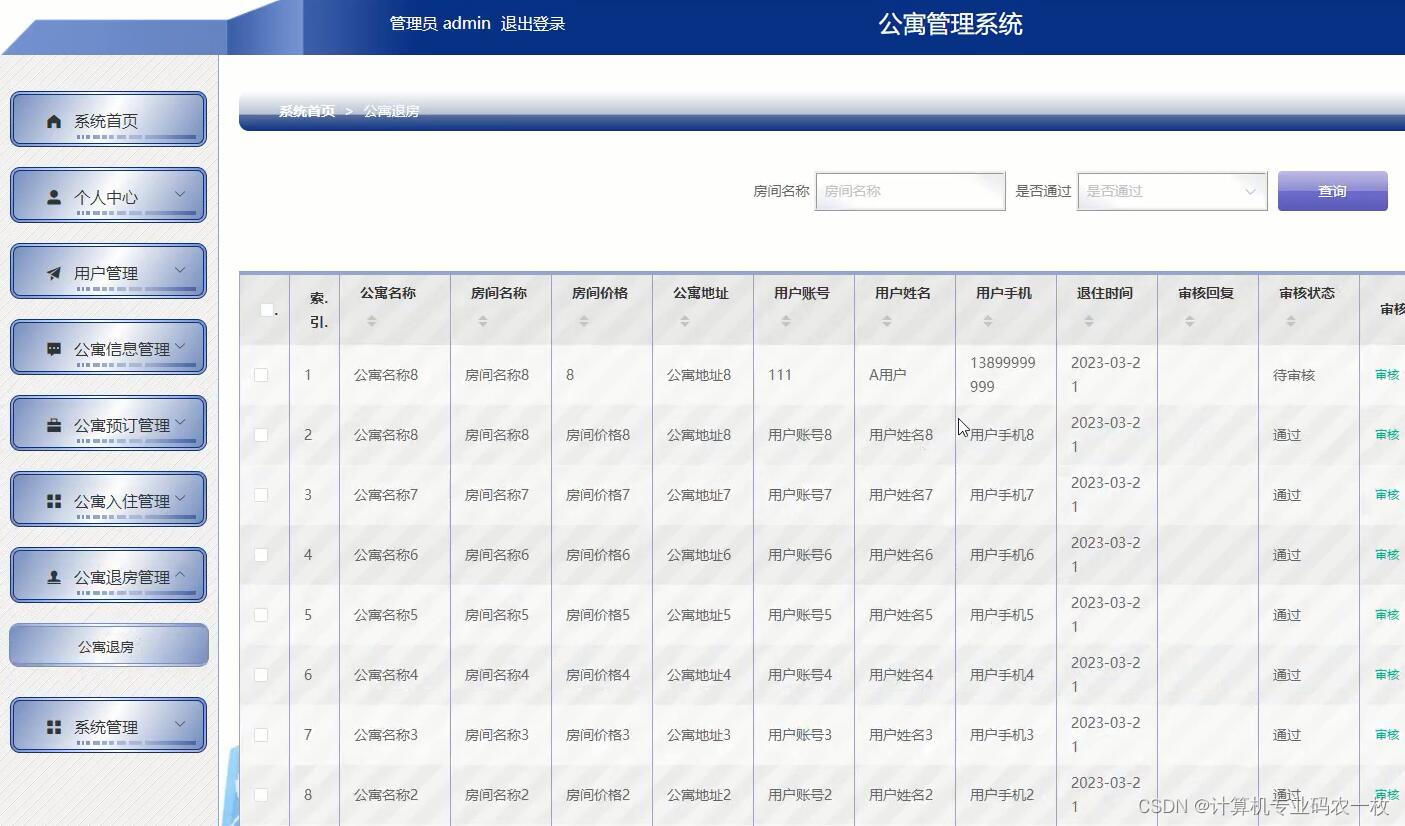
前后端分离Vue+nodejs酒店公寓客房预订管理系统udr7l-java-php-django-springboot
本系统的设计与实现共包含13个表:分别是关于我们信息表,配置文件信息表,公寓信息评论表信息表,公寓入住信息表,公寓退房信息表,公寓信息信息表,公寓预订信息表,系统公告信息表,收藏表…...

VUE打包的dist文件放到后端一起发布
背景 前后端分离开发的项目,在部署时为了方便部署,使用集成部署的方式(即前后端在一起部署的方式) 问题 直接将前端打包好的dist文件夹下的内容,放到后端项目的resource/static目录下,但是在启动访问时发…...
React入门之React_渲染基础用法和class实例写法
渲染元素 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>04元素渲染</title><script src&…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
