可以用numpy为for加速
Numpy除了用于科学计算,还有一个功能是可以代替某些for循环,进行同样的功能实现,有于是向量矩阵运算,碰到复杂的for时,计算速度可以提高,从而提高程序性能。以下是一些常用的NumPy函数和操作,可以替代多个for循环:
-
向量化操作:NumPy中的函数和操作都是针对整个数组进行的,而不是逐个元素进行操作。这样可以避免使用for循环来遍历数组,并且可以利用底层优化实现高效的计算。实例如下
import numpy as np# 创建两个数组 a = np.array([1, 2, 3]) b = np.array([4, 5, 6])# 使用向量化操作计算两个数组的和 c = a + b print(c) # 输出: [5 7 9] -
广播(Broadcasting):NumPy中的广播功能可以自动处理不同形状的数组之间的运算,而无需显式地编写循环。广播可以将较小的数组自动扩展为较大的数组,以便进行元素级别的操作。
广播的实例:import numpy as np# 创建一个数组和一个标量 a = np.array([1, 2, 3]) b = 2# 使用广播将标量与数组相加 c = a + b print(c) # 输出: [3 4 5] -
聚合函数:NumPy提供了许多聚合函数(如sum、mean、max、min等),可以对整个数组或指定轴上的元素进行聚合操作。这些函数可以避免使用for循环来逐个元素进行计算。
聚合函数的实例:import numpy as np# 创建一个二维数组 a = np.array([[1, 2, 3], [4, 5, 6]])# 对整个数组进行求和 sum_a = np.sum(a) print(sum_a) # 输出: 21# 按列求和 sum_axis0 = np.sum(a, axis=0) print(sum_axis0) # 输出: [5 7 9]# 按行求和 sum_axis1 = np.sum(a, axis=1) print(sum_axis1) # 输出: [6 15] -
矩阵运算:NumPy提供了矩阵运算的函数和操作,如矩阵乘法、转置、逆矩阵等。这些函数可以直接对整个矩阵进行操作,而无需使用for循环逐个元素进行计算。
矩阵运算的实例:import numpy as np# 创建两个矩阵 a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]])# 矩阵乘法 c = print(c) # 输出: [[19 22]# [43 50]]# 矩阵转置 d = np.transpose(a) print(d) # 输出: [[1 3]# [2 4]]# 矩阵逆矩阵 e = np.linalg.inv(a) print(e) # 输出: [[-2. 1. ]# [ 1.5 -0.5]] -
条件操作:NumPy提供了一些函数和操作,可以根据条件对数组进行操作。例如,可以使用np.where函数根据条件选择数组中的元素,而无需使用for循环逐个元素进行判断。
条件操作的实例:import numpy as np# 创建一个数组 a = np.array([1, 2, 3, 4, 5])# 根据条件选择数组中的元素 b = np.where(a > 2, a, 0) print(b) # 输出: [0 0 3 4 5] -
向量化函数:NumPy提供了许多向量化函数,可以对整个数组进行元素级别的操作。这些函数可以直接应用于数组,而无需使用for循环逐个元素进行计算。
向量化函数的实例:import numpy as np# 创建一个数组 a = np.array([1, 2, 3])# 使用向量化函数计算数组的平方根 b = np.sqrt(a) print(b) # 输出: [1. 1.41421356 1.73205081]
相关文章:

可以用numpy为for加速
Numpy除了用于科学计算,还有一个功能是可以代替某些for循环,进行同样的功能实现,有于是向量矩阵运算,碰到复杂的for时,计算速度可以提高,从而提高程序性能。以下是一些常用的NumPy函数和操作,可…...

cartographer ceres后端优化
这里引用一篇文章 https://zhuanlan.zhihu.com/p/567635409 因为cartographer中的代码有的地方添加了AddParameterBlock,有的地方没有添加,会引起歧义,原来AddParameterBlock可以隐式添加优化变量,这篇文章介绍了具体原因,核心内容如下: AddParameterBlock的作用作用一:…...
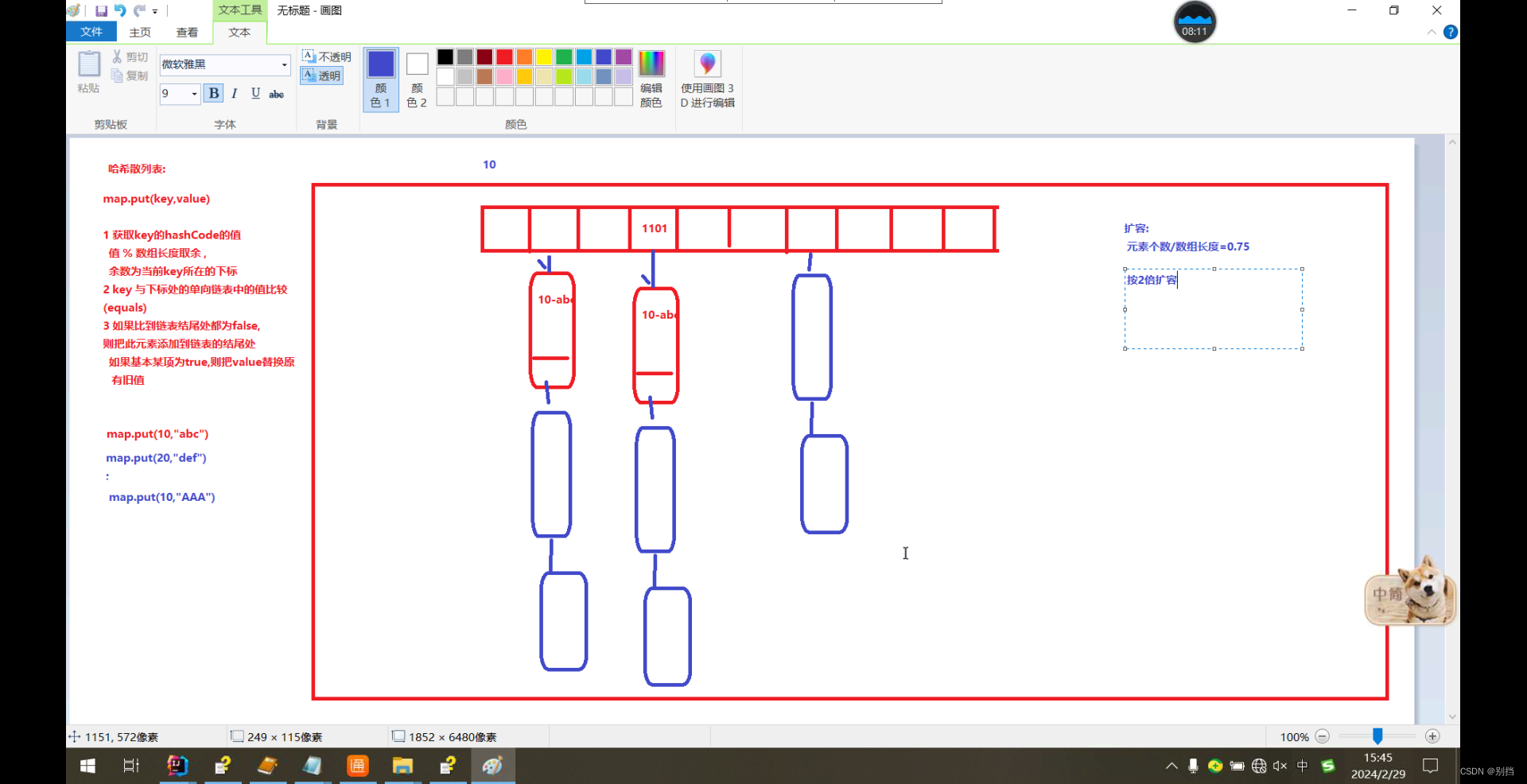
day57 集合 List Set Map
List实现类 List接口特点:元素有序 可重复 Arraylist 可变数组 jdk 8 以前Arraylist容量初始值10 jdk8 之后初始值为0,添加数据时,容量为10; ArrayList与Vector的区别? LinkList:双向链表 优点࿱…...

蓝桥杯:真题讲解3(C++版)附带解析
报纸页数 来自:2016年七届省赛大学C组真题(共8道题) 分析: --画出报纸长的样子,如果我们在上面多画一张报纸,那么就符合题意的5,6,11,12。 观察这张图:观察3…...
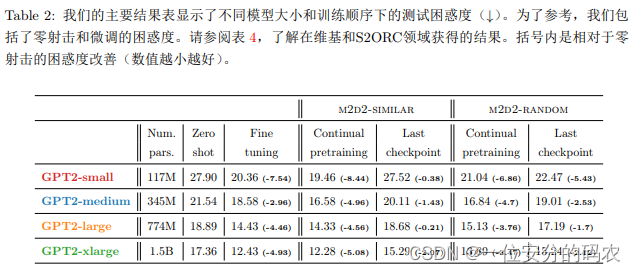
继续预训练对大语言模型的影响
翻译自文章:Investigating Continual Pretraining in Large Language Models: Insights and Implications 摘要 本文研究了大型语言模型(LLMs)中不断学习(CL)的不断发展领域,重点是制定有效和可持续的训练…...

关于空频变换的知识点
1.DCT变换: 离散余弦变换是一种将图像从空域转换到频域的技术,它可以将图像分解为频域分量。对于RGB图像,它由红色(R)、绿色(G)和蓝色(B)三个通道组成。当应用DCT变换时…...

纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐
纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐 使用flex实现 思路 容器样式(.container): Flex容器的BFC性质使得其内部的子元素(.text-box)在水平方向上能够居中,通过justify-c…...
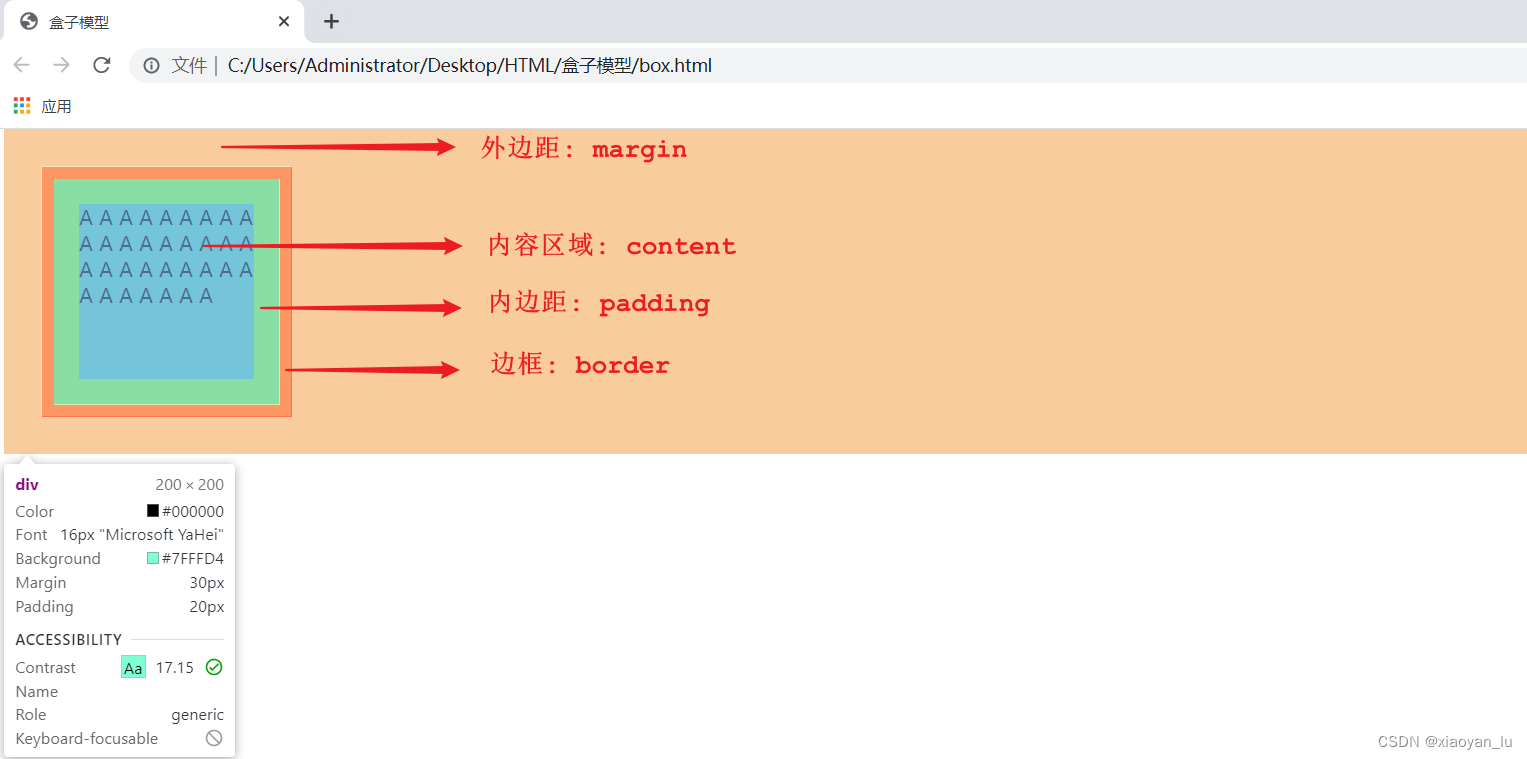
初学HTMLCSS——盒子模型
盒子模型 盒子:页面中所有的元素(标签),都可以看做是一个 盒子,由盒子将页面中的元素包含在一个矩形区域内,通过盒子的视角更方便的进行页面布局盒子模型组成:内容区域(content&…...
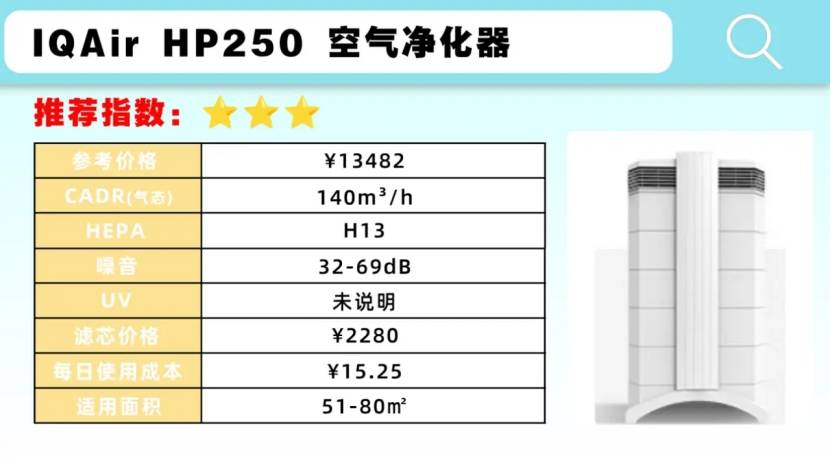
吸猫毛空气净化器哪个好?推荐除猫毛好的宠物空气净化器品牌
如今,越来越多的家庭选择养宠物!虽然家里变得更加温馨,但养宠可能会带来异味和空气中的毛发增多可能会引发健康问题,这也是一个大问题。 但我不想家里到处都是异味,尤其是便便的味道,所以很需要一款能够处…...

【玩转408数据结构】线性表——双链表、循环链表和静态链表(线性表的链式表示 下)
知识回顾 在前面的学习中,我们已经了解到了链表(线性表的链式存储)的一些基本特点,并且深入的研究探讨了单链表的一些特性,我们知道,单链表在实现插入删除上,是要比顺序表方便的,但是…...
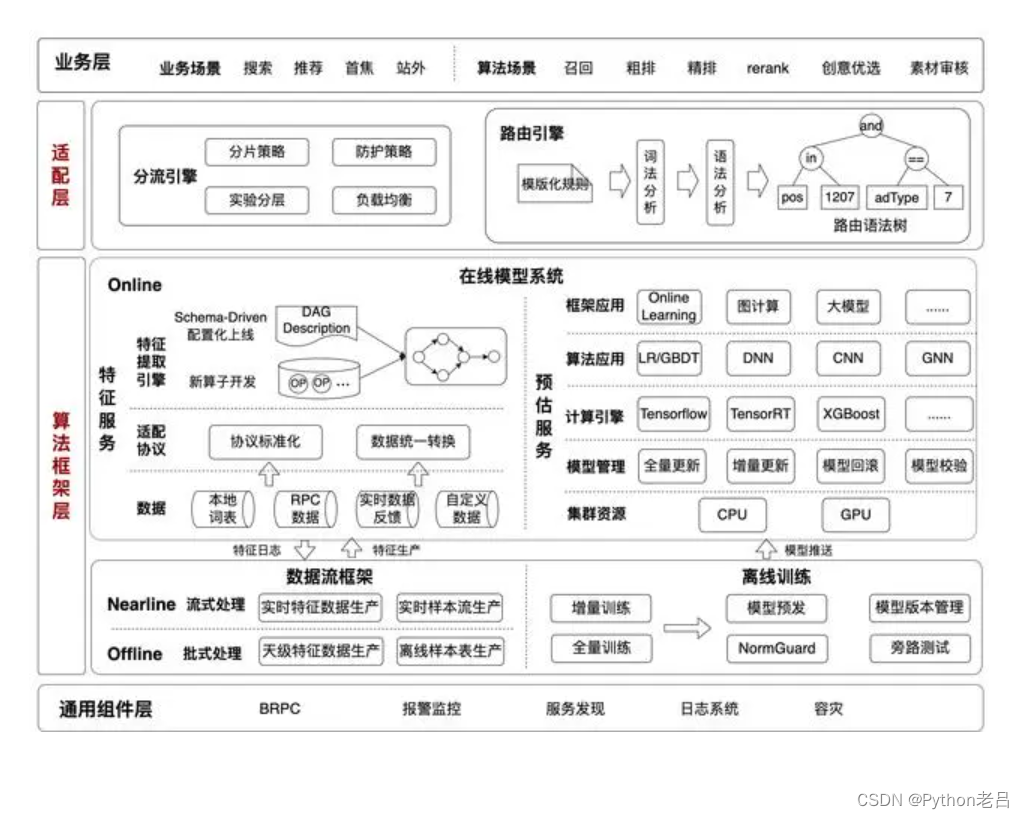
分布式概念
分布式概念 一、分布式介绍1.1 分布式计算1.1.1 分布式计算的方法1.1.1 分布式计算与互联网的普及1.1.2 分布式计算项目1.1.3 参与计算 1.2 分布式存储系统1.2.1 P2P 数据存储系统1.2.2 云存储系统 1.3 应用 二、分布式基础概念2.1 微服务2.2 集群2.3 分布式2.4 节点2.5 远程调…...

vue中的ref/reactive区别及原理
Vue中的ref和reactive是两种不同的数据响应式管理方式。 ref是Vue 3中新加入的特性,它可以将一个普通的JavaScript对象转换为响应式对象。通过ref创建的响应式对象在访问和修改时会自动触发重新渲染。ref返回的是一个包含value属性的对象,访问或修改数据…...
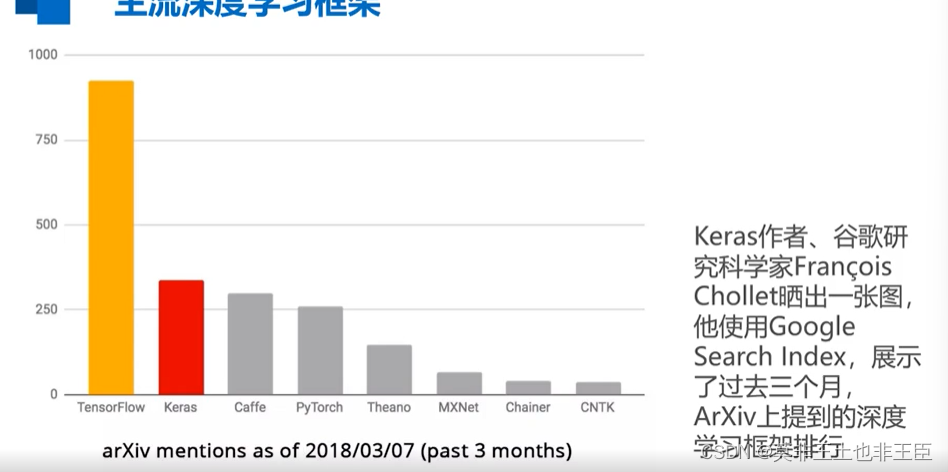
深度学习介绍与环境搭建
深度学习介绍与环境搭建 慕课大学人工智能学习笔记,自己学习记录用的。(赋上连接) https://www.icourse163.org/learn/ZUCC-1206146808?tid1471365447#/learn/content?typedetail&id1256424053&cid1289366515人工智能、机器学习与…...
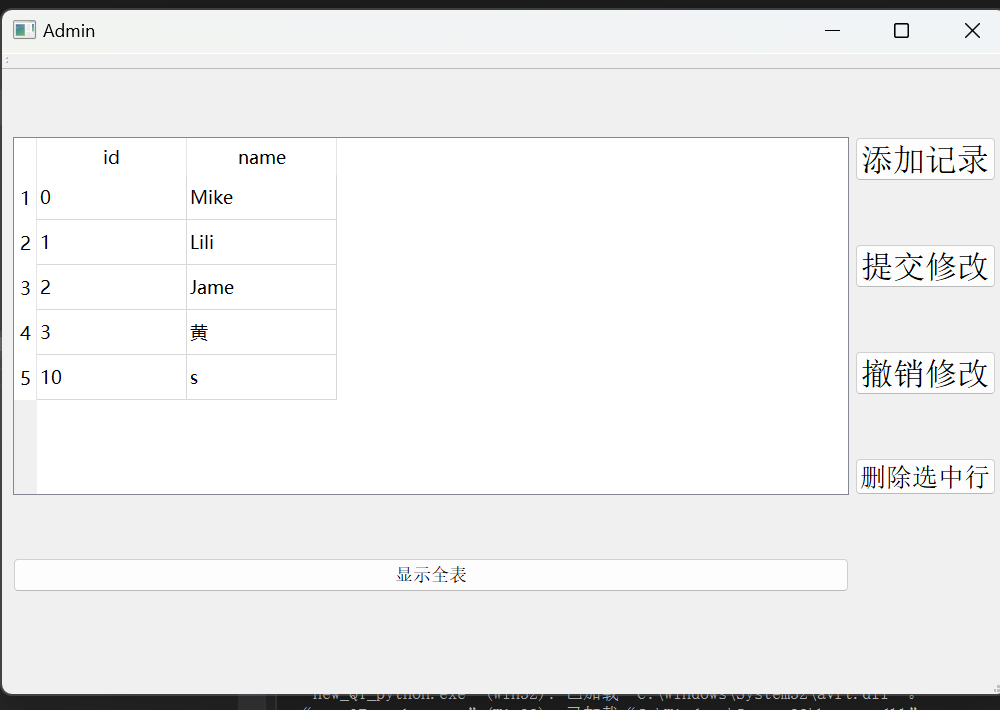
QT C++实践|超详细数据库的连接和增删改查操作|附源码
0:前言 🪧 什么情况需要数据库? 1 大规模的数据需要处理(比如上千上万的数据量)2 需要把数据信息存储起来,无论是本地还是服务上,而不是断电后数据信息就消失了。 如果不是上面的原因化,一般…...

matlab:涉及复杂函数图像的交点求解
matlab:涉及复杂函数图像的交点求解 在MATLAB中求解两个图像的交点是一个常见的需求。本文将通过一个示例,展示如何求解两个图像的交点,并提供相应的MATLAB代码。 画出图像 首先,我们需要绘制两个图像,以便直观地看…...
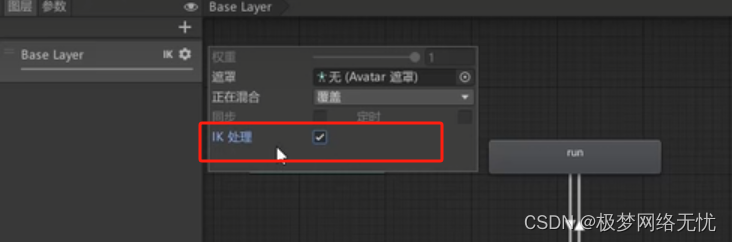
Unity(第二十二部)官方的反向动力学一般使用商城的IK插件,这个用的不多
反向动力学(Inverse Kinematic,简称IK)是一种通过子节点带动父节点运动的方法。 正向动力学 在骨骼动画中,大多数动画是通过将骨架中的关节角度旋转到预定值来生成的,子关节的位置根据父关节的旋转而改变,这…...

nginx反向代理,获取客户端ip
一、获取客户端ip代码 /*** description: 获取客户端IP* return string*/ public static function getClientIp(){$ip ;if(getenv(HTTP_CLIENT_IP) && strcasecmp(getenv(HTTP_CLIENT_IP),unknown)){$ip getenv(HTTP_CLIENT_IP);}else if(getenv(HTTP_X_FORWARDED_F…...
G. The Morning Star(简单容斥))
13 Codeforces Round 886 (Div. 4)G. The Morning Star(简单容斥)
G. The Morning Star 思路:用map记录x,y,以及y-x、yx从前往后统计一遍答案即可公式 a n s c n t [ x ] c n t [ y ] − 2 ∗ c n t [ x , y ] c n t [ y x ] c n t [ y − x ] anscnt[x]cnt[y]-2 * cnt[x,y]cnt[yx]cnt[y-x] anscnt[x]…...

CLion 2023:专注于C和C++编程的智能IDE mac/win版
JetBrains CLion 2023是一款专为C和C开发者设计的集成开发环境(IDE),它集成了许多先进的功能,旨在提高开发效率和生产力。 CLion 2023软件获取 CLion 2023的智能代码编辑器提供了丰富的代码补全和提示功能,使您能够更…...
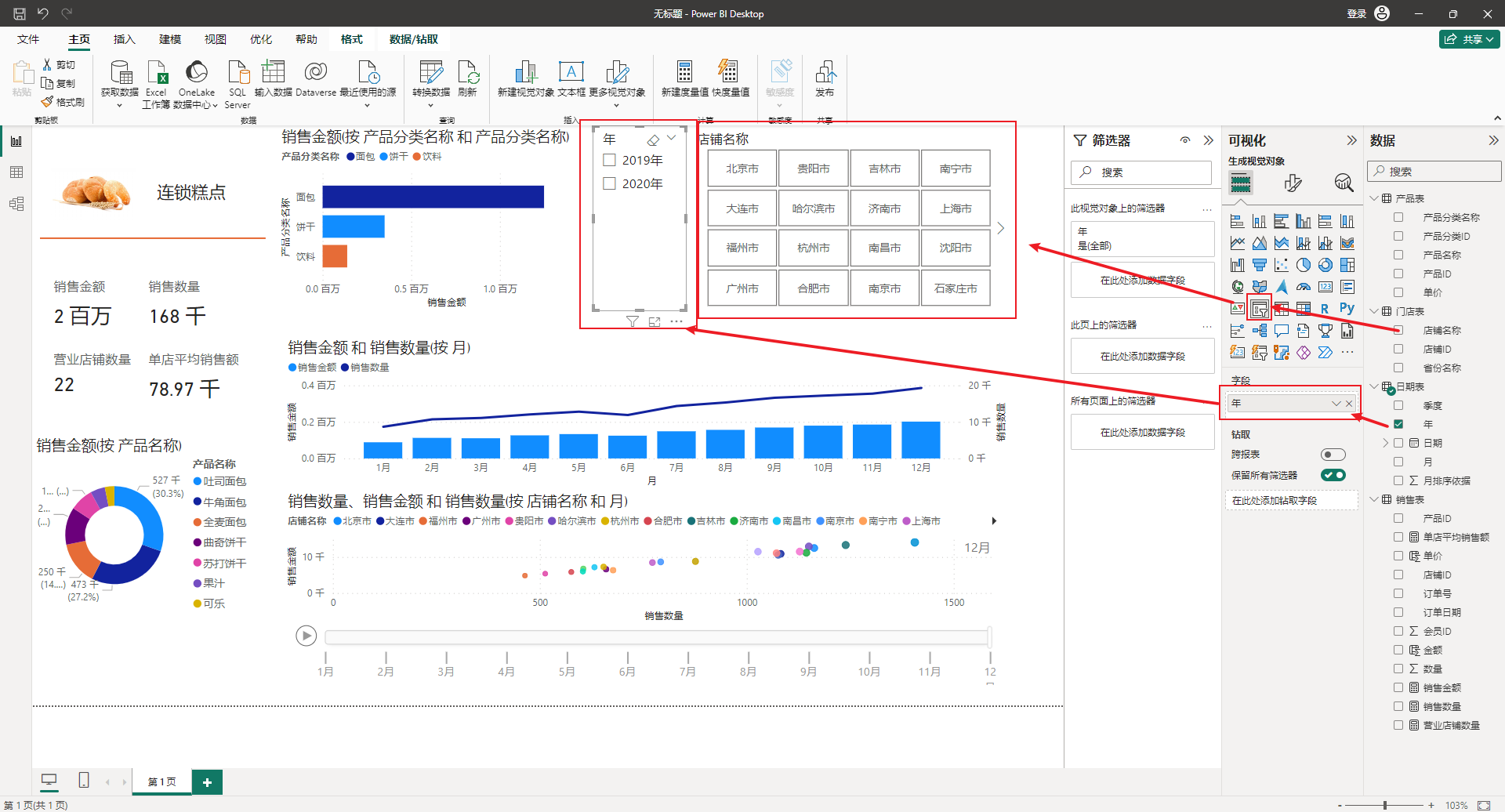
数据可视化基础与应用-02-基于powerbi实现连锁糕点店数据集的仪表盘制作
总结 本系列是数据可视化基础与应用的第02篇,主要介绍基于powerbi实现一个连锁糕点店数据集的仪表盘制作。 数据集描述 有一个数据集,包含四张工作簿,每个工作簿是一张表,其中可以销售表可以划分为事实表,产品表&am…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...
