c/c++|红黑树|分析应用|锚点
红黑树是一种自平衡的二叉查找树,它保持着良好的平衡,能够在插入和删除等操作后通过一系列旋转和重新着色操作来保持树的平衡。这种平衡性质使得红黑树在搜索、插入和删除等操作的平均和最坏情况下的时间复杂度都是O(log n)。以下是红黑树的一些关键特性和性质:每个节点要么是红色,要么是黑色。
根节点必须是黑色。
红色节点的子节点必须是黑色(不存在两个相邻的红色节点)。
从任一节点到其每个叶子的所有路径都包含相同数量的黑色节点,这被称为“黑色平衡”或“黑高度”。
红黑树的基本操作包括插入、删除、查找等。其中,插入和删除操作是通过一系列旋转和重新着色来维护红黑树的平衡性。插入操作:当插入一个新节点时,首先按照二叉查找树的规则找到其应该插入的位置。然后,将新节点插入为红色节点,这样可能会破坏红黑树的某些性质,如颜色相邻节点不能同时为红色。接下来,通过一系列的旋转和重新着色操作来修复这些性质,以确保树的平衡性。删除操作:删除操作也是通过一系列旋转和重新着色来维护树的平衡性。当删除一个节点时,首先按照二叉查找树的规则找到要删除的节点。然后,根据要删除节点的子节点情况进行不同的处理:如果要删除的节点有零个或一个子节点,直接删除即可;如果要删除的节点有两个子节点,则需要找到其后继节点(即比它大的最小节点),并用后继节点替换原节点,然后再删除后继节点。查找操作:查找操作和普通的二叉查找树一样,采用递归或迭代的方式从根节点开始逐级查找,直到找到目标节点或到达叶子节点为止。红黑树的时间复杂度和空间复杂度分析如下:时间复杂度:在红黑树中,搜索、插入和删除操作的平均和最坏情况下的时间复杂度都是O(log n),其中n是树中节点的数量。这是因为红黑树保持了良好的平衡性质,使得树的高度保持在O(log n)级别。因此,即使在最坏情况下,搜索、插入和删除操作的性能也是很高效的。空间复杂度:红黑树的空间复杂度主要取决于节点的数量。每个节点除了存储数据外,还需要存储指向父节点、左子节点和右子节点的指针,以及颜色信息。因此,红黑树的空间复杂度为O(n),其中n是树中节点的数量。
#include <iostream>enum Color { RED, BLACK };template <typename T>
struct Node {T data;Node<T> *left, *right, *parent;Color color;// ConstructorNode(T data) : data(data), left(nullptr), right(nullptr), parent(nullptr), color(RED) {}
};template <typename T>
class RedBlackTree {
private:Node<T> *root;// Private methodsvoid rotateLeft(Node<T> *&);void rotateRight(Node<T> *&);void fixInsertion(Node<T> *&);public:// ConstructorRedBlackTree() : root(nullptr) {}// Public methodsvoid insert(const T&);void printInorder() const;
};// Rotate left
template <typename T>
void RedBlackTree<T>::rotateLeft(Node<T> *&node) {Node<T> *rightChild = node->right;node->right = rightChild->left;if (node->right != nullptr)node->right->parent = node;rightChild->parent = node->parent;if (node->parent == nullptr)root = rightChild;else if (node == node->parent->left)node->parent->left = rightChild;elsenode->parent->right = rightChild;rightChild->left = node;node->parent = rightChild;
}// Rotate right
template <typename T>
void RedBlackTree<T>::rotateRight(Node<T> *&node) {Node<T> *leftChild = node->left;node->left = leftChild->right;if (node->left != nullptr)node->left->parent = node;leftChild->parent = node->parent;if (node->parent == nullptr)root = leftChild;else if (node == node->parent->left)node->parent->left = leftChild;elsenode->parent->right = leftChild;leftChild->right = node;node->parent = leftChild;
}// Fix insertion
template <typename T>
void RedBlackTree<T>::fixInsertion(Node<T> *&node) {Node<T> *parent = nullptr;Node<T> *grandparent = nullptr;while (node != root && node->color != BLACK && node->parent->color == RED) {parent = node->parent;grandparent = parent->parent;// Case : Parent is left child of Grandparentif (parent == grandparent->left) {Node<T> *uncle = grandparent->right;// Case : Uncle is RED, only recoloring requiredif (uncle != nullptr && uncle->color == RED) {grandparent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandparent;} else {// Case : Node is right child of Parentif (node == parent->right) {rotateLeft(parent);node = parent;parent = node->parent;}// Case : Node is left child of ParentrotateRight(grandparent);std::swap(parent->color, grandparent->color);node = parent;}} else {// Case : Parent is right child of GrandparentNode<T> *uncle = grandparent->left;// Case : Uncle is RED, only recoloring requiredif (uncle != nullptr && uncle->color == RED) {grandparent->color = RED;parent->color = BLACK;uncle->color = BLACK;node = grandparent;} else {// Case : Node is left child of Parentif (node == parent->left) {rotateRight(parent);node = parent;parent = node->parent;}// Case : Node is right child of ParentrotateLeft(grandparent);std::swap(parent->color, grandparent->color);node = parent;}}}root->color = BLACK;
}// Insert node into the tree
template <typename T>
void RedBlackTree<T>::insert(const T& data) {Node<T> *newNode = new Node<T>(data);Node<T> *parent = nullptr;Node<T> *current = root;while (current != nullptr) {parent = current;if (newNode->data < current->data)current = current->left;elsecurrent = current->right;}newNode->parent = parent;if (parent == nullptr)root = newNode;else if (newNode->data < parent->data)parent->left = newNode;elseparent->right = newNode;fixInsertion(newNode);
}// Inorder traversal
template <typename T>
void inorderHelper(Node<T> *root) {if (root == nullptr) return;inorderHelper(root->left);std::cout << root->data << " ";inorderHelper(root->right);
}// Print tree in inorder
template <typename T>
void RedBlackTree<T>::printInorder() const {inorderHelper(root);
}// Test
int main() {RedBlackTree<int> tree;tree.insert(10);tree.insert(20);tree.insert(30);tree.insert(15);tree.insert(25);std::cout << "Inorder traversal of the tree: ";tree.printInorder();std::cout << std::endl;return 0;
}//输出结果:Inorder traversal of the tree: 10 15 20 25 30
先让gpt回答吧
怎么说呢,说到红黑树,必然先从avl 平衡二叉树讲起
而且红黑树在unordered_map、redis、等数据存储用很多应用
平衡性维护方式:AVL树:通过保持任意节点的左子树和右子树的高度差不超过1来维护平衡。在插入或删除节点时,可能需要进行旋转操作来保持平衡。
红黑树:通过一系列的旋转和重新着色操作来维护平衡。红黑树不追求严格的平衡,但它保证了树的黑高度是O(log n),从而保证了树的高度近似平衡。
旋转次数:AVL树:由于 AVL 树要求严格的平衡,插入或删除操作可能需要进行更多的旋转操作来保持平衡,因此在某些情况下,AVL树的旋转次数会比红黑树多。
红黑树:红黑树的平衡性维护更加宽松,旋转和重新着色的次数相对较少,因此在实践中通常比 AVL 树更高效。
性能特点:AVL树:由于 AVL 树严格追求平衡,因此在查找操作上可能比红黑树更快,因为 AVL 树的高度更低。但是在插入和删除操作上可能更耗时,因为可能需要进行更多的旋转操作。
红黑树:红黑树在插入和删除操作上的性能通常比 AVL 树更好,因为它的平衡性维护更加宽松,旋转和重新着色的次数较少。红黑树在实际应用中更为广泛,例如在C++的STL中就使用了红黑树来实现map和set等容器。
总的来说,AVL树和红黑树都是自平衡的二叉查找树,它们各有优缺点,在不同的应用场景中选择合适的数据结构是很重要的。
关联容器的实现:红黑树常被用作关联容器的底层实现,例如C++ STL中的std::map和std::set就是基于红黑树实现的。这些容器可以快速地进行查找、插入和删除操作,并且保持元素的有序性。数据库索引:数据库系统中经常需要快速地查找和更新数据,红黑树作为一种高效的数据结构,常被用作数据库索引的底层实现。它可以支持快速的数据检索操作,并且保持索引的平衡性。操作系统内核:红黑树在操作系统内核中也有广泛的应用,用于实现各种数据结构和算法。例如,在Linux内核中,红黑树被用于进程调度、文件系统、内存管理等方面。路由表:计算机网络中的路由器常使用红黑树来存储路由表,以支持快速的路由查找和更新。红黑树可以高效地存储和管理大量的网络路由信息,并且保持路由表的平衡性。内存分配器:在动态内存分配器中,红黑树可以用于管理内存分配和释放的元数据,以支持快速的内存分配和释放操作,并且保持内存分配器的高效性和平衡性。总的来说,红黑树作为一种高效的自平衡二叉查找树,具有广泛的应用领域,可以在各种场景中提供高效的数据存储和检索功能。
相关文章:

c/c++|红黑树|分析应用|锚点
红黑树是一种自平衡的二叉查找树,它保持着良好的平衡,能够在插入和删除等操作后通过一系列旋转和重新着色操作来保持树的平衡。这种平衡性质使得红黑树在搜索、插入和删除等操作的平均和最坏情况下的时间复杂度都是O(log n)。以下是红黑树的一些关键特性…...

2-29算法习题总结
贪心问题 小A的糖果 题目描述 小 A 有 n n n 个糖果盒,第 i i i 个盒中有 a i a_i ai 颗糖果。 小 A 每次可以从其中一盒糖果中吃掉一颗,他想知道,要让任意两个相邻的盒子中糖的个数之和都不大于 x x x,至少得吃掉几颗糖…...

当Linux 磁盘满了,查看大文件并删除
当你的Linux磁盘空间满了时,可以通过以下步骤查找大文件并删除它们: 检查磁盘空间: 使用以下命令检查磁盘空间的使用情况: df -h这将显示文件系统的使用情况,包括每个文件系统的总大小、已用空间、可用空间和挂载点。 …...

STL -萃取特性迭代器
1. STL简单概述 a. STL六大组成部分 容器(Container)空间配置器(allocator)算法(Algorithm)迭代器(Iterator)仿函数(Function object)适配器(Ad…...

python pandas写入csv
在Python的Pandas库中,可以使用to_csv方法将DataFrame对象写入CSV文件。以下是一个简单的示例: import pandas as pd# 创建一个DataFrame对象 data {Name: [Alice, Bob, Charlie, David],Age: [25, 30, 35, 40],City: [New York, Los Angeles, Chicago…...

oracle 数据库建集群式数据库的DBLINK的语法
根据需要修改以下红色字体的部分即可。 1、连接集群式数据库DBLINK语法 create public database link 自定义的dblink名字 connect to 连接对方数据库的用户名 identified by "密码" using (DESCRIPTION (ADDRESS_LIST (FAILOVER ON) (LOAD_BALANCE OFF) …...

基于JAVA的毕业设计分配选题系统 开源项目
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 专业档案模块2.2 学生选题模块2.3 教师放题模块2.4 选题审核模块 三、系统展示四、核心代码4.1 查询专业4.2 新增专业4.3 选择课题4.4 取消选择课题4.5 审核课题 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpri…...

Android 接入指纹识别
接入指纹框架:https://github.com/Tencent/soter implementation com.github.Tencent.soter:soter-wrapper:2.0.91.Application中初始化 class IApplication : Application() {override fun onCreate() {super.onCreate()instance thisinitSort()}private fun in…...

如何通过代理IP安全使用Linkedln领英?
LinkedIn是跨境外贸必备的拓客工具,世界各地的许多专业人士都使用领英来作为发布和共享内容的主要工具,这使得它成为跨境出海必备的渠道工具。 但是不少做外贸的朋友都知道,领英账号很容易遭遇限制封禁,但如果善用工具࿰…...

嵌入式驱动学习第一周——定时器与延时函数
前言 这篇博客一起学习定时器,定时器是最常用到的功能之一,其最大的作用之一就是提供了延时函数。 嵌入式驱动学习专栏将详细记录博主学习驱动的详细过程,未来预计四个月将高强度更新本专栏,喜欢的可以关注本博主并订阅本专栏&…...

Tips杂记
🥲 🥸 🤌 🫀 🫁 🥷 🐻❄️🦤 🪶 🦭 🪲 🪳 🪰 🪱 🪴 🫐 🫒 🫑…...

可以用numpy为for加速
Numpy除了用于科学计算,还有一个功能是可以代替某些for循环,进行同样的功能实现,有于是向量矩阵运算,碰到复杂的for时,计算速度可以提高,从而提高程序性能。以下是一些常用的NumPy函数和操作,可…...

cartographer ceres后端优化
这里引用一篇文章 https://zhuanlan.zhihu.com/p/567635409 因为cartographer中的代码有的地方添加了AddParameterBlock,有的地方没有添加,会引起歧义,原来AddParameterBlock可以隐式添加优化变量,这篇文章介绍了具体原因,核心内容如下: AddParameterBlock的作用作用一:…...
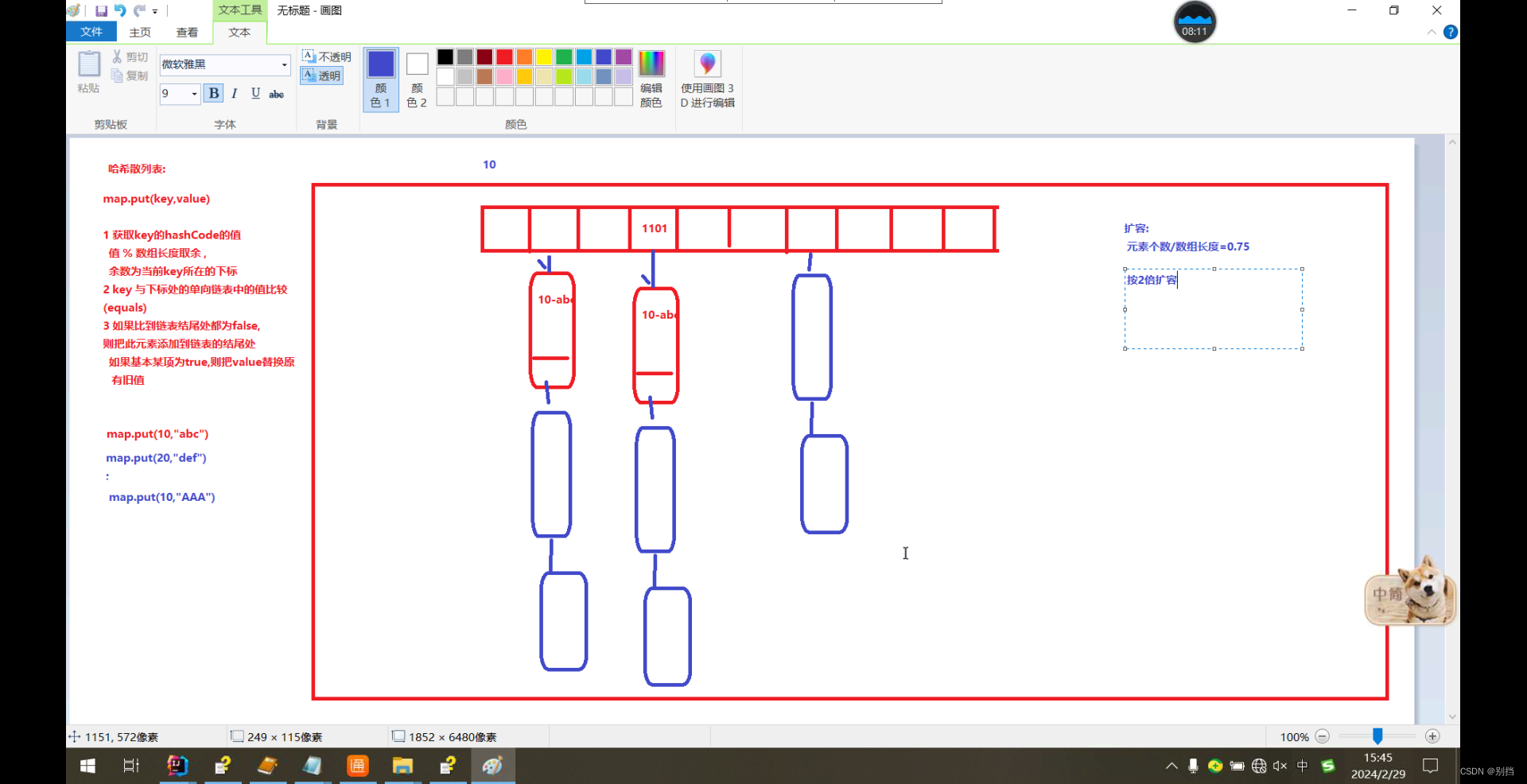
day57 集合 List Set Map
List实现类 List接口特点:元素有序 可重复 Arraylist 可变数组 jdk 8 以前Arraylist容量初始值10 jdk8 之后初始值为0,添加数据时,容量为10; ArrayList与Vector的区别? LinkList:双向链表 优点࿱…...

蓝桥杯:真题讲解3(C++版)附带解析
报纸页数 来自:2016年七届省赛大学C组真题(共8道题) 分析: --画出报纸长的样子,如果我们在上面多画一张报纸,那么就符合题意的5,6,11,12。 观察这张图:观察3…...
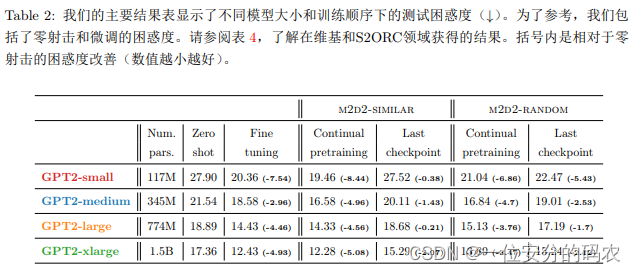
继续预训练对大语言模型的影响
翻译自文章:Investigating Continual Pretraining in Large Language Models: Insights and Implications 摘要 本文研究了大型语言模型(LLMs)中不断学习(CL)的不断发展领域,重点是制定有效和可持续的训练…...

关于空频变换的知识点
1.DCT变换: 离散余弦变换是一种将图像从空域转换到频域的技术,它可以将图像分解为频域分量。对于RGB图像,它由红色(R)、绿色(G)和蓝色(B)三个通道组成。当应用DCT变换时…...

纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐
纯css实现-让字符串在文字少时显示为居中对齐,而在文字多时显示为左对齐 使用flex实现 思路 容器样式(.container): Flex容器的BFC性质使得其内部的子元素(.text-box)在水平方向上能够居中,通过justify-c…...
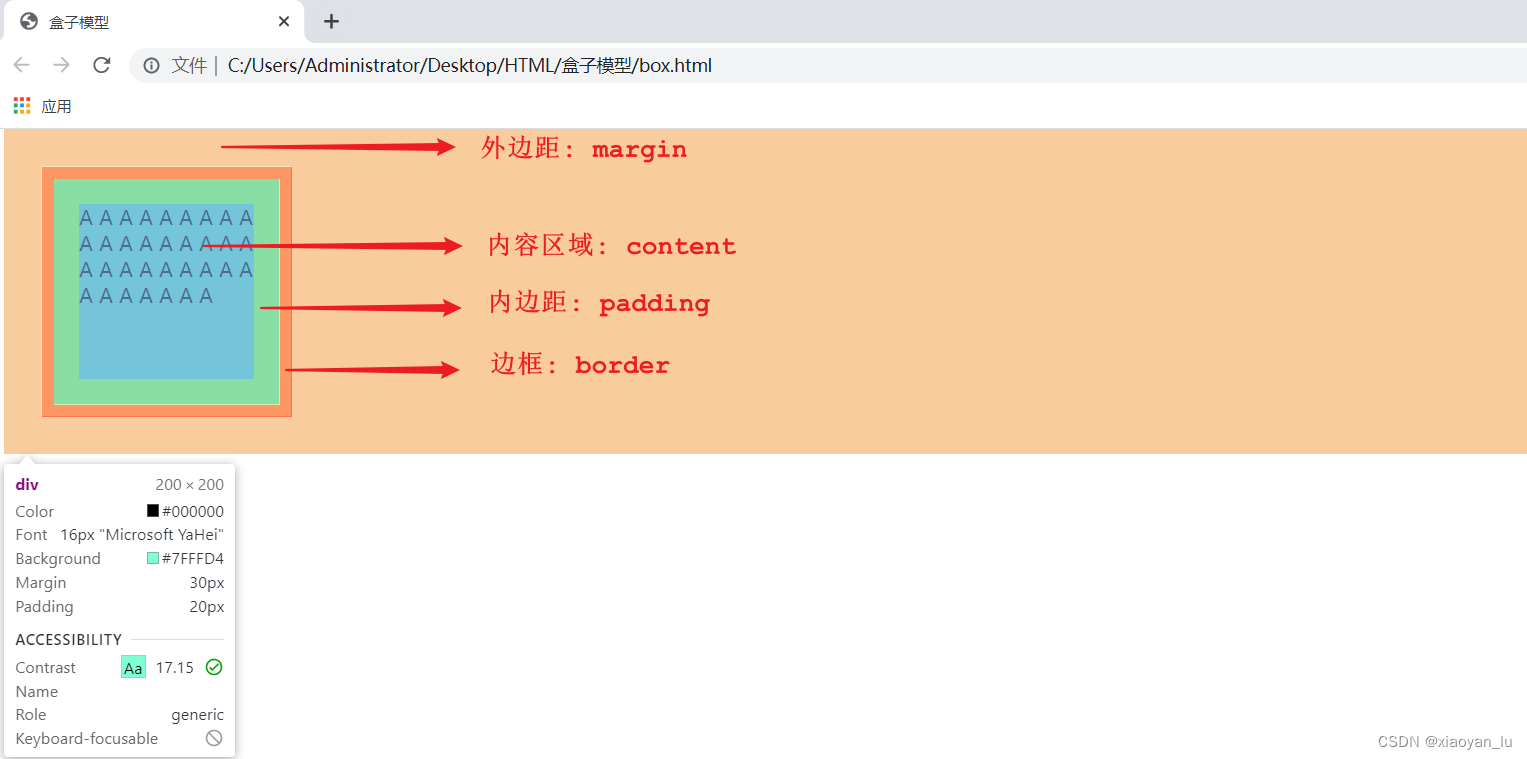
初学HTMLCSS——盒子模型
盒子模型 盒子:页面中所有的元素(标签),都可以看做是一个 盒子,由盒子将页面中的元素包含在一个矩形区域内,通过盒子的视角更方便的进行页面布局盒子模型组成:内容区域(content&…...
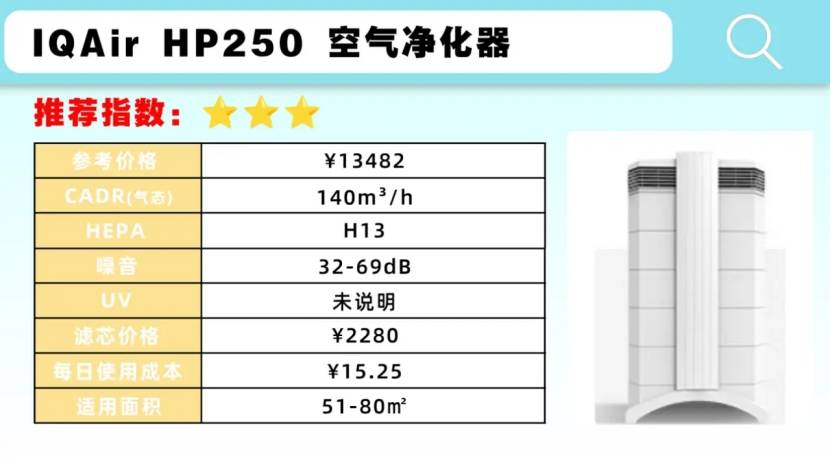
吸猫毛空气净化器哪个好?推荐除猫毛好的宠物空气净化器品牌
如今,越来越多的家庭选择养宠物!虽然家里变得更加温馨,但养宠可能会带来异味和空气中的毛发增多可能会引发健康问题,这也是一个大问题。 但我不想家里到处都是异味,尤其是便便的味道,所以很需要一款能够处…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
